Astronet > Dvizhushiesya obolochki zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Dvizhushiesya obolochki zvezd << 4.1 Atom s tremya urovnyami | Oglavlenie | 4.3 Rol' stolknovenii i obshego poglosheniya v obolochke >>

4.2 Real'nyi atom

Rassmotrim teper' real'nyi atom, obladayushii beskonechnym chislom urovnei. Uslovie stacionarnosti dlya i-go urovnya imeet vid

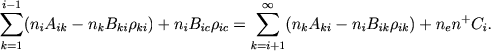
$\sum\limits_{k=1}^{i-1} (n_i A_{ik} - n_k B_{ki}\rho_{ki})+n_i B_{ic}\rho_{ic} = \sum\limits_{k=i+1}^\infty (n_k A_{ki} - n_i B_{ik}\rho_{ik})+n_e n^+ C_{i} .$ (39)

Ispol'zuya oboznacheniya, vvedennye v predydushem pragrafe, my mozhem napisat'

$\left. \begin{array}{l} n_k A_{ki} - n_i B_{ik}\rho_{ik} = 4\pi a_{ik}(C_{ik}-\bar K_{ik}) \\ n_e n^+ C_{i} - n_i B_{ic}\rho_{ic} = 4\pi a_{ic}(C_{ic}-\bar K_{ic}) \end{array} \right\}$ (40)

Poetomu vmesto (39) poluchaem

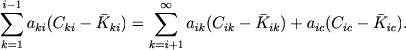
$\sum\limits_{k=1}^{i-1} a_{ki}(C_{ki}-\bar K_{ki}) = \sum\limits_{k=i+1}^\infty a_{ik}(C_{ik}-\bar K_{ik}) + a_{ic}(C_{ic}-\bar K_{ic}) .$ (41)

K etim usloviyam luchevogo ravnovesiya nado prisoedinit' eshe uravneniya perenosa izlucheniya. Dlya izlucheniya v nepreryvnom spektre my kak vsegda imeem

$\cos\theta\frac{dK_{ic}}{dt_{ic}} = -K_{ic} + C_{ic} ,$ (42)

a dlya izlucheniya v spektral'nyh liniyah po analogii s uravneniem (18) predydushego paragrafa poluchaem

$\cos\theta\frac{dK_{ik}}{dt_{ik}} = -(1+\beta_{ik}\cos^2\theta)K_{ik} + C_{ik} ,$ (43)

gde velichina β_ik ravna

$\beta_{ik} = \frac{1}{2u} \cdot \frac{dv}{dt_{ik}} .$ (44)

Sistema uravnenii (41), (42) i (43) predstavlyaet gromadnye trudnosti dlya resheniya. Dlya nepodvizhnoi obolochki, t. e. pri β_ik=0, eta sistema byla rassmotrena V. A. Ambarcumyanom [2] i Henyey [8]. Pri etom byli polucheny neskol'ko pervyh integralov sistemy ("integraly potoka"). Legko videt', chto v rassmatrivaemom sluchae, t. e. pri nalichii gradienta skorosti, integraly potoka ne sushestvuyut.

Odnako nalichie gradienta skorosti privodit k sushestvennomu uprosheniyu vysheprivedennoi sistemy. Esli gradient skorosti dostatochno velik, to dlya kazhdogo elementarnogo ob'ema v srednih chastyah obolochki mozhet schitat'sya vypolnennym sleduyushee uslovie: kolichestvo kvantov, izluchaemyh v spektral'noi linii, ravnyaetsya chislu kvantov, pogloshaemyh v etoi linii, i chislu kvantov, uhodyashih iz obolochki vsledstvie effekta Doplera. V sluchae plosko-parallel'nyh sloev eto uslovie imeet vid

$C_{ik} = \bar K_{ik} + \frac{\beta_{ik}}{3}\bar K_{ik} .$ (45)

To obstoyatel'stvo, chto eto uslovie deistvitel'no dolzhno vypolnyat'sya, vytekaet iz rezul'tatov, poluchennyh v predydushem paragrafe. V samom dele, predpolagaya vypolnennym neravenstvo (25), my poluchili, chto v srednih chastyah obolochki plotnost' izlucheniya opredelyaetsya formulami (32)(prichem, kak legko videt', etot rezul'tat ne zavisit ot granichnyh uslovii dlya izlucheniya v linii). No my prishli by k tem zhe samym formulam (32), esli by, naryadu s uravneniyami (14) i (16), rassmotreli ne uravnenie perenosa (18), a sootnoshenie (45) dlya chastoty ν₁₂. Eto znachit, chto pri vypolnenii neravenstva (26) mozhet schitat'sya vypolnennym i sootnoshenie (45).

Prinimaya sootnoshenie (45) i schitaya, kak i ran'she, chto opticheskaya tolshina obolochki za granicami subordinatnyh serii men'she edinicy (togda velichiny ρ_2c, ρ_3c... budut zadannymi), my vidim, chto zadacha sostoit v sushnosti v tom, chtoby naiti plotnost' izlucheniya za granicei osnovnoi serii (ibo esli vse velichiny ρ_ic izvestny, to nahozhdenie stepeni vozbuzhdeniya v kazhdom meste obolochki pri nalichii sootnosheniya (45) predstavlyaet algebraicheskuyu operaciyu). Konechno, na samom dele velichina ρ_1c sama zavisit ot stepeni vozbuzhdeniya, no my seichas pokazhem, chto dlya priblizhennogo nahozhdeniya etoi velichiny dostatochno prinyat' vo vnimanie tol'ko dva pervyh urovnya.

Skladyvaya pochlenno vse uravneniya (41), nachinaya so vtorogo, poluchaem

$\sum\limits_{i=2}^\infty a_{1i}(C_{1i}-\bar K_{1i}) = \sum\limits_{i=2}^\infty a_{ic}(C_{ic}-\bar K_{ic}) .$ (46)

No

$a_{ic} C_{ic} = \frac{p_i}{p_1} a_{1c}C_{1c} ,$ (47)

gde p_i - dolya zahvatov na i-uroven', i

$a_{ic}\bar K_{ic} = a_{1c}\frac{B_{ic}\rho_{ic}}{q_1 A_{i1}} \bar K_{1c} ,$ (48)

gde q_i=a_1c/a_1i. Krome togo, my mozhem ispol'zovat' sootnoshenie (45) dlya linii osnovnoi serii. Togda vmesto (46) nahodim

$\frac{\beta_{12}}{3}\sum\limits_{i=2}^\infty \bar K_{1i} = q_2 \frac{1-p_1}{p_1} C_{1c} - \sum\limits_{i=2}^\infty \frac{q_2}{q_i} \frac{B_{ic} \rho_{ic}}{A_{i1}} \bar K_{1i} .$ (49)

Pervoe zhe iz uravnenii (41) privoditsya k vidu

$\frac{\beta_{12}}{3}\sum\limits_{i=2}^\infty K_{1i} + q_2 (C_{1c} - \bar K_{1c}) = 0 .$ (50)

Legko poluchit' sleduyushee sootnoshenie:

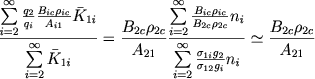
$\frac{\sum\limits_{i=2}^\infty \frac{q_2}{q_i} \frac{B_{ic} \rho_{ic}}{A_{i1}} \bar K_{1i}}{\sum\limits_{i=2}^\infty \bar K_{1i}} = \frac{B_{2c} \rho_{2c}}{A_{21}} \frac{\sum\limits_{i=2}^\infty \frac{B_{ic} \rho_{ic}}{B_{2c} \rho_{2c}} n_i}{\sum\limits_{i=2}^\infty \frac{\sigma_{1i} g_{2}}{\sigma_{12} g_{i}} n_i} \simeq \frac{B_{2c} \rho_{2c}}{A_{21}}$ (51)

(tak kak v obeih poluchennyh summah glavnuyu rol' igrayut pervye chleny). Poetomu iz (49) i (50) nahodim

$\left(\beta_{12} + 3p_1 \frac{B_{2c} \rho_{2c}}{A_{21}}\right)C_{1c} = \left(\beta_{12} + 3\frac{B_{2c} \rho_{2c}}{A_{21}}\right)p_1 \bar K_{1c} .$ (52)

Poluchennoe uravnenie vmeste s sootvetstvuyushim uravneniem perenosa izlucheniya (42) i reshayut zadachu o ionizacii v obolochke. No legko videt', chto uravnenie (52) my poluchili by, uchityvaya tol'ko dva pervyh urovnya. Sledovatel'no, zadacha o vozbuzhdenii i ionizacii real'nyh atomov deistvitel'no svoditsya k zadache, rassmotrennoi v predydushem paragrafe.

<< 4.1 Atom s tremya urovnyami | Oglavlenie | 4.3 Rol' stolknovenii i obshego poglosheniya v obolochke >>

Publikacii s klyuchevymi slovami: obolochki zvezd - perenos izlucheniya Publikacii so slovami: obolochki zvezd - perenos izlucheniya
Sm. takzhe: Sbrasyvayushaya massivnuyu obolochku zvezda G79.29+0.46 Obnaruzhenie goryachego vodyanogo para v obolochke uglerodnoi zvezdy. Obolochki v tumannosti Yaico Osveshennost' Planetarnye tumannosti

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce