Astronet > Dvizhushiesya obolochki zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Dvizhushiesya obolochki zvezd << 4.2 Real'nyi atom | Oglavlenie | 4.4 Nekotorye primeneniya >>

4.3 Rol' stolknovenii i obshego poglosheniya v obolochke

Nalichie gradienta skorosti ne yavlyaetsya edinstvennoi prichinoi, vedushei k ponizheniyu stepeni vozbuzhdeniya i ionizacii atomov. Takoe zhe vliyanie okazyvayut udary vtorogo roda i obshee pogloshenie v obolochke. My seichas rassmotrim kazhduyu iz etih prichin v otdel'nosti.

a) Stolknoveniya

Pri nesootvetstvii mezhdu stepen'yu vozbuzhdeniya atomov i elektronnoi temperaturoi, stolknoveniya mezhdu atomami i elektronami vedut k umen'sheniyu etogo nesootvetstviya. Esli stepen' vozbuzhdeniya nizhe bol'cmanovskoi pri temperature elektronnogo gaza, to udary pervogo roda proishodyat chashe udarov vtorogo roda i vedut k povysheniyu stepeni vozbuzhdeniya i ponizheniyu elektronnoi temperatury. Pri obratnom polozhenii chashe proishodyat udara vtorogo roda, i eto vedet k ponizheniyu stepeni vozbuzhdeniya i povysheniyu elektronnoi temperatury. V gazovyh tumannostyah osushestvlyaetsya pervyi iz etih sluchaev; v obolochkah malogo radiusa mogut, po-vidimomu, osushestvlyat'sya oba eti sluchaya.

Dopustim, chto imeet mesto vtoroi iz ukazannyh sluchaev, i vyyasnim podrobnee rol' stolknovenii. Kak i v § 1, voz'mem atom s tremya urovnyami. Dlya ucheta udarov vtorogo roda my dolzhny v pravoi chasti pervrgo iz uravnenii (2) dobavit' chlen n₂n_eD₂₁. Togda vmesto pervogo iz sootnoshenii (14) poluchaem

$C_{12} = \left(1-\frac{\gamma}{3}\right) \bar K_{12} + q(1-p)\bar K_{13} - \frac{n_2 n_e D_{21}}{4\pi a_{12}} .$ (53)

No

$\frac{n_2}{4\pi a_{12}} = \frac{\bar K_{12}}{A_{21}} .$ (54)

Poetomu, perehodya k uravneniyam (22), my vmesto vtorogo iz etih uravnenii nahodim

$q^2 \frac{d^2 \bar K_{12}}{d\tau^2} = (\beta + \gamma + \delta)\bar K_{12} - 3(1-p)q\bar K_{13},$ (55)

gde oboznacheno

$\frac{\delta}{3} = \frac{n_e D_{21}}{A_{21}} .$ (56)

My vidim, chto vliyanie udarov vtorogo roda formal'no skazyvaetsya tak zhe, kak nalichie gradienta skorosti.

Dlya ocenki velichiny δ my mozhem vospol'zovat'sya formuloi (III, 49), opredelyayushei velichiny D_1k dlya vodorodnogo atoma. Tak kak

$D_{21} = \frac{g_1}{g_2} e^{\frac{h\nu_{12}}{kT}} D_{12} ,$ (57)

to pri T=10000°; (velichina D₂₁, vprochem, ochen' slabo zavisit ot T) my nahodim

$\delta \approx 10^{-17} n_e .$ (58)

Dlya zvezdnyh obolochek, rassmotrennyh nami v glave II, bylo polucheno β > 10^-8, n_e < 10¹². Eto znachit, chto v takih obolochkah β >> δ, t. e. gradient skorosti igraet gorazdo bol'shuyu rol', chem udary vtorogo roda. Dlya obolochek novyh zvezd polozhenie yavlyaetsya analogichnym.

b) Obshee pogloshenie v obolochke

Pri nalichii obshego poglosheniya v obolochke umen'shenie stepeni vozbuzhdeniya i ionizacii proishodit kak blagodarya poglosheniyu kvantov, izluchaemyh dannymi atomami za granicami serii, tak i blagodarya poglosheniyu kvantov, izluchaemyh v spektral'nyh liniyah. Chtoby rassmotret' etot effekt, nado dobavit' sootvetstvuyushie chleny k uravneniyam perenosa izlucheniya, napisannym vyshe. (Usloviya luchevogo ravnovesiya pri etom, ochevidno, ne izmenyatsya).

Voz'mem snova atom s tremya urovnyami. Vmesto uravnenii (16) i (18) my teper' imeem

$\cos\theta\frac{dK_{13}}{d\tau} = -(1+\eta)K_{13} + C_{13} ,$ (59)

$\cos\theta\frac{dK_{12}}{dt} = -(1+\eta_1 + \beta\cos^2\theta)K_{12} + C_{12} ,$ (60)

gde

$\eta = \frac{a_{13}^\prime}{a_{13}}, \quad \eta_1 = \frac{a_{12}^\prime}{a_{12}},$ (61)

a a'₁₃ i a'₁₂ - koefficienty obshego poglosheniya za granicei osnovnoi serii i v spektral'noi linii.

Iz uravnenii (59) i (60) s pomosh'yu uslovii luchevogo ravnovesiya poluchaem

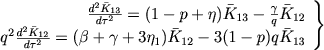
$\left. \begin{array}{r} \frac{d^2 \bar K_{13}}{d\tau^2} = (1 - p + \eta)\bar K_{13} - \frac{\gamma}{q} \bar K_{12} \\ q^2 \frac{d^2 \bar K_{12}}{d\tau^2} = (\beta + \gamma + 3\eta_1)\bar K_{12} - 3(1-p)q\bar K_{13} \end{array} \right \}$ (62)

[vmesto uravnenii (22)]. Harakteristicheskoe uravnenie etoi sistemy imeet vid

$[\lambda^2 - 3(1-p+\eta)][q^2 \lambda^2 - (\beta + \gamma + 3\eta_1)] = 3(1-p)\gamma$ (63)

i, esli schitat' vypolnennym neravenstvo (26), to dlya λ₁ nahodim

$\lambda^2_1 = 3\left[\eta + (1-p)\frac{3\eta_1 +\beta}{3\eta_1 +\beta +\gamma}\right].$ (64)

Trudno skazat', ne imeya v vidu konkretnyh obolochek i atomov, kakoi iz chlenov, vhodyashih v etu formulu, igraet naibol'shuyu rol'. Otmetim tol'ko, chto v obolochkah zvezd pozdnih klassov rol' obshego poglosheniya ves'ma znachitel'na. Poetomu podrobnee etot vopros budet rassmotren v sleduyushei glave.

<< 4.2 Real'nyi atom | Oglavlenie | 4.4 Nekotorye primeneniya >>

Publikacii s klyuchevymi slovami: obolochki zvezd - perenos izlucheniya Publikacii so slovami: obolochki zvezd - perenos izlucheniya
Sm. takzhe: Sbrasyvayushaya massivnuyu obolochku zvezda G79.29+0.46 Obnaruzhenie goryachego vodyanogo para v obolochke uglerodnoi zvezdy. Obolochki v tumannosti Yaico Osveshennost' Planetarnye tumannosti

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

$\cos\theta\frac{dK_{13}}{d\tau} = -(1+\eta)K_{13} + C_{13} ,$	(59)
$\cos\theta\frac{dK_{12}}{dt} = -(1+\eta_1 + \beta\cos^2\theta)K_{12} + C_{12} ,$	(60)