Astronet > Dvizhushiesya obolochki zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Dvizhushiesya obolochki zvezd << 4.3 Rol' stolknovenii i obshego poglosheniya v obolochke | Oglavlenie | Glava V. Zvezdy pozdnih spektral'nyh klassov s yarkimi liniyami >>

4.4 Nekotorye primeneniya

Nesomnenno, chto vyvedennye nami formuly dolzhny prinimat'sya vo vnimanie pri reshenii mnogih voprosov, kasayushihsya tumannyh obolochek, okruzhayushih zvezdy. Nekotorye iz etih voprosov rassmotreny nizhe.

a) Neodnorodnaya obolochka

V glave II k neodnorodnym obolochkam zvezd my primenili rezul'taty, poluchennye nami v glave I dlya odnorodnoi sredy. Togda my ne mogli obosnovat' zakonnost' etogo primeneniya, tak kak v nashem rasporyazhenii ne bylo uravneniya perenosa izlucheniya v spektral'noi linii. My sdelaem eto seichas, vzyav dlya prostoty atom s tremya urovnyami.

V dannom sluchae plotnost' izlucheniya v linii opredelyaetsya vtorym iz uravnenii (22), v kotorom vse velichiny β, γ i $\bar K_{13}$ yavlyayutsya zadannymi funkciyami ot r. Nashe priblizhenie sostoit v tom, chto v srednih chastyah obolochki plotnost' izlucheniya v linii schitaetsya ravnoi

$\bar K_{12} = \frac{3(1-p)q}{\beta +\gamma}\bar K_{13}.$ (65)

Iz ukazannogo uravneniya vytekaet sleduyushee neravenstvo, dayushee ocenku uslovii, pri kotoryh eto priblizhenie yavlyaetsya spravedlivym:

$\frac{d^2}{dt^2}\left(\frac{\bar K_{13}}{\beta +\gamma}\right)\ll \bar K_{13} .$ (66)

Dlya modeli obolochki, rassmotrennoi v glave II, my imeem

$\bar K_{13} \sim \left(\frac{r_0}{r} \right)^2,\; dt = a_{12}^0 \left(\frac{r_0}{r} \right)^2 dr,\; \beta = \frac{v}{3u}\frac{1}{a_{12}^0 r_0} \frac{r}{r_0} .$

chto β >> γ tak kak v obratnom sluchae raspredelenie atomov po sostoyaniyam vo vsei obolochke yavlyaetsya blizkim k bol'cmanovskomu. Dlya takoi obolochki neravenstvo (66) privoditsya k vidu

$\frac{18}{a_{12}^0 r_0} \frac{u}{v} \frac{r}{r_0} \ll 1.$ (67)

Tak kak obychno $a_{12}^0 r_0 \approx 10^4,\, \frac{u}{v} \approx 0,01$ , to eto neravenstvo na vsem protyazhenii obolochki mozhet schitat'sya vypolnennym v ves'ma sil'noi stepeni.

b) Temperatura zvezd

Kak izvestno, metod Zanstra dlya opredeleniya temperatur zvezd, okruzhennyh nebulyarnymi obolochkami, osnovan na predpolozhenii, chto svechenie obolochki v liniyah kakogo-libo elementa proishodit za schet energii zvezdy za granicei osnovnoi serii. Odnako v sluchae obolochek malogo radiusa v izluchenie linii perehodit ne tol'ko energiya zvezdy za granicei osnovnoi serii, no i za granicami subordinatnyh serii. Poetomu temperatury zvezd, opredelyaemye metodom Zanstra bez ucheta etogo obstoyatel'stva, mogut okazat'sya zavyshennymi.

Gordeladze [4] ocenil velichinu etogo effekta, ispol'zuya teoriyu vozbuzhdeniya i ionizacii v obolochkah malogo radiusa, dannuyu V. A. Ambarcumyanom [1]. On nashel, chto v sluchae zvezd tipa Vol'fa-Raie temperatury, opredelennye po liniyam ionizovannogo geliya i drugih atomov s vysokim potencialom ionizacii, poluchayushiesya gorazdo bolee vysokimi, chem po liniyam vodoroda, dolzhny byt' pri uchete etogo effekta znachitel'no ponizheny.

Odnako teoriya V. A. Ambarcumyana ne uchityvaet dvizheniya obolochki. My seichas ocenim velichinu etogo effekt, ispol'zuya nashi formuly, poluchennye vyshe. Pust' obolochka pogloshaet vsyu energiyu zvezdy za granicei osnovnoi serii. Chislo pogloshennyh kvantov budet ravno

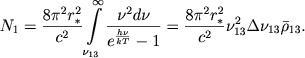
$N_1 = \frac{8\pi^2 r_*^2}{c^2} \int\limits_{\nu_{13}}^\infty \frac{\nu^2 d \nu}{e^{\frac{h\nu}{kT}}-1} = \frac{8\pi^2 r_*^2}{c^2} \nu_{13}^2 \Delta\nu_{13} \bar \rho_{13}.$ (68)

Naidem teper' chislo kvantov za granicei subordinatnoi serii, pogloshennyh obolochkoi. My, ochevidno, imeem

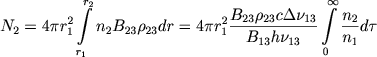
$N_2 = 4\pi r_1^2 \int\limits_{r_1}^{r_2} n_2 B_{23} \rho_{23} dr = 4\pi r_1^2 \frac{B_{23} \rho_{23} c \Delta\nu_{13}}{B_{13} h\nu_{13}} \int\limits_0^\infty \frac{n_2}{n_1} d\tau$ (69)

ili, ispol'zuya pervuyu iz formul (35),

$N_2 = 4\pi r_1^2 \frac{B_{23} \rho_{23} c \Delta\nu_{13}}{pB_{13} h\nu_{13}} \frac{g_2}{g_1} \bar \rho_{12} \frac{\gamma}{\beta}.$ (70)

Dlya otnosheniya N₂/N₁ poluchaem

$\frac{N_2}{N_1} = \frac{g_2}{g_1} \frac{B_{23}}{B_{13}} \frac{\bar \rho_{12} \bar \rho_{23}}{p \bar \rho_{13}} \left(\frac{\nu_{23}}{\nu_{13}}\right)^3 \frac{\gamma}{\beta} \simeq \frac{\gamma}{\beta}.$ (71)

Eto vyrazhenie dolzhno byt' podstavleno v sleduyushee uravnenie

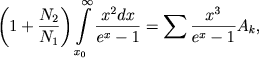
$\left(1+\frac{N_2}{N_1}\right)\int\limits_{x_0}^\infty \frac{x^2 dx}{e^x -1} = \sum \frac{x^3}{e^x - 1} A_k ,$ (72)

yavlyayusheesya obobsheniem uravneniya Zanstra (III,60). Zdes' summirovanie vedetsya po liniyam rassmatrivaemogo atoma.

Vychisleniya pokazyvayut, chto velichina γ/β obychno poryadka edinicy. Poetomu my prihodim k vyvodu, chto rassmatrivaemyi effekt ne igraet zametnoi roli (dlya ionizovannogo geliya eta velichina dolzhna byt' poryadka 10⁸, chtoby temperatura zvezdy "povysilas'" s 20000°; do 50000°;). Deistvitel'noe ob'yasnenie ukazannogo vyshe rashozhdeniya mezhdu temperaturami, opredelennymi po liniyam razlichnyh atomov, dano v § 1 glavy II.

v) Temperatura obolochek

opros o temperaturah obolochek malogo radiusa (v chastnosti - obolochek novyh zvezd) yavlyaetsya v nastoyashee vremya Sovershenno neyasnym. Obychno schitaetsya, chto temperatura obolochki prosto ravna temperature zvezdy. Dlya vyyasneniya etogo voprosa, principial'no govorya, mozhno ispol'zovat' metod, predlozhennyi nami dlya opredeleniya temperatur gazovyh tumannostei (glava III, § 3). Odnako iz-za slozhnosti yavlenii, proishodyashih v obolochkah malogo radiusa, tochnye podschety poka zatrudnitel'ny.

My vse zhe mozhem otmetit' odno obstoyatel'stvo, otlichayushee obolochki malogo radiusa ot gazovyh tumannostei. Tak kak ionizaciya v etih obolochkah proishodit ne tol'ko iz osnovnogo, no i iz vozbuzhdennyh sostoyanii, to srednyaya energiya, poluchaemaya elektronami pri ionizacii, v etom sluchae znachitel'no men'she, chem v tumannostyah. Provedem illyustrativnyi podschet dlya vodorodnoi obolochki, prenebregaya stolknoveniyami.

Uslovie ravenstva chisla ionizacii i rekombinacii k zakon sohraneniya energii dlya svobodnyh elektronov obolochki mogut byt' zapisany v vide

$\sum\limits_1^\infty n_i B_{ic} \rho_{ic} = n_e n^+ \sum\limits_1^\infty C_i ,$ (73)

$\sum\limits_1^\infty n_i B_{ic} \rho_{ic} \epsilon_{ic} = n_e n^+ (\sum\limits_1^\infty C_i \epsilon_i + f),$ (74)

gde ε_ic est' srednyaya energiya, poluchaemaya elektronom pri fotoionizacii s i-go urovnya, a ostal'nye oboznacheniya prinyaty takimi zhe, kak v § 3 glavy III.

Dopustim, kak i ran'she, chto opticheskaya tolshina obolochki za granicei osnovnoi serii gorazdo bol'she edinicy a za granicami subordinatnyh serii men'she edinicy. Togda vse kvanty, izluchaemye obolochkoi za granicei osnovnoi serii, budut pogloshat'sya v samoi obolochke. Poetomu vmesto (73) i (74) my poluchaem

$\sum\limits_1^\infty n_i B_{ic} \rho_{ic}^0 = n_e n^+ \sum\limits_2^\infty C_i ,$ (75)

$\sum\limits_1^\infty n_i B_{ic} \rho_{ic}^0 \epsilon_{ic}^0 = n_e n^+ (\sum\limits_2^\infty C_i \epsilon_i + f),$ (76)

gde cherez ρ_ic⁰ oboznachena plotnost' izlucheniya, prihodyashego neposredstvenno ot zvezdy, a cherez ε_ic⁰ - sootvetstvuyushaya energiya, poluchaemaya elektronom pri ionizacii.

Pust' N_i est' chislo ionizacii, proishodyashih iz i-go sostoyaniya vo vsei obolochke, t. e.

$N_i = \int n_i B_{ic} \rho_{ic}^0 d\nu .$ (77)

Iz sootnoshenii (75) i (76) my nahodim

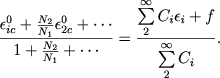
$\frac{\epsilon_{ic}^0 + \frac{N_2}{N_1} \epsilon_{2c}^0 + \cdots}{1+ \frac{N_2}{N_1} + \cdots} = \frac{\sum\limits_2^\infty C_i \epsilon_i + f}{\sum\limits_2^\infty C_i} .$ (78)

Tak zhe, kak v glave III, eto sootnoshenie mozhet byt' preobrazovano k vidu

$\frac{A_{1} + \frac{N_2}{N_1} A_2 + \cdots}{1+ \frac{N_2}{N_1} + \cdots} T_* = BT_e ,$ (79)

gde velichina A₁ opredelyaetsya formuloi (III, 42), a velichiny A₂, A₃, ... - formuloi (41), v kotoroi nado schitat' $x_0 = \frac{h\nu_{ic}}{kT}$ (ibo za granicei osnovnoi serii pogloshaetsya vse izluchenie, idushee ot zvezdy, a za granicami subordinatnyh serii - tol'ko nebol'shaya chast' izlucheniya). Sootnoshenie (79) daet iskomuyu svyaz' mezhdu T_∗ i T_e.

Dopustim dlya primera, chto bol'she vsego ionizacii proishodit iz vtorogo sostoyaniya. Togda vmesto (79) imeem

$A_2 T_* = BT_e .$ (80)

Pri T_∗=20000°; iz tabl. XI nahodim A₂=0,71 (eto znachenie beretsya iz pervoi chasti ukazannoi tablicy pri temperature v 4 raza bol'shei temperatury zvezdy). S etim znacheniem A₂ dlya elektronnoi temperatury poluchaem T_e=12000°;. Zametim, chto esli by bylo N₂/N₁ < 1, to dlya T_e poluchilos' by znachenie poryadka 20000°; .

Kak uzhe skazano, provedennyi podschet ne pretenduet na tochnost', ibo my ne uchityvali stolknovenii, kotorye mogut kak ponizhat', tak i povyshat' temperaturu obolochki (sootvetstvenno udary pervogo i vtorogo roda).

Sleduet takzhe imet' v vidu, chto temperatura raznyh chastei obolochki mozhet byt' razlichnoi. V takom sluchae temperatura vneshnih chastei dolzhna byt' bolee nizkoi, chem vnutrennih. Eto obuslovleno dvumya prichinami: 1) padeniem stepeni vozbuzhdeniya i ionizacii pri perehode ot vnutrennei granicy obolochki k vneshnei i 2) polnym ekranirovaniem izlucheniya zvezdy za granicei osnovnoi serii. Vsledstvie etogo elektrony poluchayut pri ionizacii nebol'shuyu energiyu i ne mogut ee uvelichit' za schet udarov vtorogo roda.

g) Svetovoe davlenie

Nesomnenno, chto svetovoe davlenie, vyzvannoe poglosheniem sveta v spektral'nyh liniyah, igraet v obolochkah novyh zvezd znachitel'nuyu rol'. Dlya primenenii vazhno dat' formuly, opredelyayushie sleduyushie velichiny: 1) svetovoe davlenie na vnutrennei granice obolochki i 2) svetovoe davlenie, deistvuyushee na vsyu obolochku.

Chtoby poluchit' eti formuly, my mozhem vospol'zovat'sya rezul'tatami, naidennymi v § 1 nastoyashei glavy. Opredelyaya proizvol'nye postoyannye, vhodyashie v vyrazheniya (23) i (24), iz granichnyh uslovii (30), my dlya potoka izlucheniya na vnutrennei granice obolochki nahodim

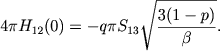
$4\pi H_{12}(0) = -q\pi S_{13}\sqrt{\frac{3(1-p)}{\beta}} .$ (81)

Svetovoe davlenie, vychislennoe s pomosh'yu etoi formuly, okazyvaetsya po poryadku velichiny sravnimym s siloi prityazheniya central'noi zvezdy.

Pri poluchenii formuly (81) my prenebregli izlucheniem v linii, padayushim na vnutrennyuyu granicu obolochki ot zvezdy. Esli uchest' eto izluchenie, to k potoku izlucheniya (81) pridetsya pribavit' sleduyushii chlen:

$4\pi H_{12}(0) = +\sqrt{\beta}\pi S_{12}.$ (82)

Nado dumat', chto etot chlen gorazdo men'she predydushego, tak kak otnoshenie S₁₃/S₁₂ , t. e. otnoshenie chisla kvantov za granicei osnovnoi serii k chislu kvantov v linii, razumeetsya, ochen' veliko.

Zametim, chto dlya ob'yasneniya yavlenii, proishodyashih v obolochkah novyh zvezd srazu posle maksimuma bleska, E. R. Mustel' [5,6] predpolagaet, chto osnovnoi siloi, deistvuyushei v obolochke v etot period, yavlyaetsya svetovoe davlenie, vyzvannoe poglosheniem kvantov, idushih neposredstvenno ot zvezdy. Potok izlucheniya na vnutrennei granice obolochki pri etom raven

$4\pi H_{12}^{\prime\prime}(0) = +\pi S_{12}.$ (83)

Chtoby soglasovat' eto predpolozhenie s nashimi rezul'tatami, nado potrebovat' vypolneniya odnogo iz dvuh uslovii: 1) gradient skorosti v obolochke ochen' velik, a energiya zvezdy za granicei osnovnoi serii nedostatochna, chtoby vyzvat' sil'nuyu flyuorescenciyu [togda budet |H₁₂(0)| < H'₁₂(0) i H'₁₂(0) ≈ H"₁₂(0)]; odnako eto oznachaet, chto nado ukazat' drugoi mehanizm (a ne flyuorescenciyu) dlya ob'yasneniya yarkih polos, nablyudayushihsya v spektrah novyh zvezd v eto vremya; 2) v obolochke otsutstvuet luchevoe ravnovesie (ob etom sm. nizhe).

Pri nahozhdenii svetovogo davleniya, deistvuyushego na vsyu obolochku, Ms Sgea [7] i Mustel' [8] predpolagali, chto lotok vnutri linii ne menyaetsya v obolochke (t. e. prinimali model' Shustera). Na samom dele nado uchityvat' kak nalichie gradienta skorosti, tak i flyuorescenciyu. Sootvetstvuyushie formuly mogut byt' legko dany s pomosh'yu rezul'tatov, poluchennyh vyshe. Odnako na etom my ne budem ostanavlivat'sya.

g) Vremya relaksacii

Dlya obolochek novyh zvezd vazhno ustanovit' "vremya relaksacii", t. e. promezhutok vremeni, neobhodimyi dlya ustanovleniya luchevogo ravnovesiya. Rezul'taty teorii luchevogo ravnovesiya mozhno primenyat' tol'ko k tem obolochkam, prodolzhitel'nost' sushestvovaniya kotoryh velika po sravneniyu s vremenem relaksacii.

Mozhno schitat', chto vremya relaksacii opredelyaetsya prodolzhitel'nost'yu nahozhdeniya svetovogo kvanta v obolochke. Poetomu dlya vychisleniya vremeni relaksacii nado razdelit' chislo kvantov, nahodyashihsya v obolochke, na chislo kvantov, pokidayushih obolochku za edinicu vremeni. Pol'zuyas' formulami (32), dlya chisla kvantov, nahodyashihsya v stolbe s secheniem 1 sm², poluchaem

$\frac{4\pi}{c}\int\limits_{r_1}^{r_2} (\bar K_{12} + \bar K_{13})dr = \frac{3}{\beta} \frac{\pi S_{13}}{ca_{13}} \left[q+\frac{\beta + \gamma}{3(1-p)}\right] .$ (84)

Tak kak chislo kvantov, uhodyashih iz etogo stolba za 1 sek., ochevidno, ravno πS₁₃, to dlya vremeni relaksacii nahodim

$T = \frac{6u}{c\frac{dv}{dr}}\left[1+\frac{\beta +\gamma}{3q(1-p)} \right] .$ (85)

V nachal'noi stadii obolochek novyh zvezd mozhno prinyat' dv/dr ≈ v/r i β + γ ≈ q. V takom sluchae formula (77) daet dlya vremeni relaksacii velichinu poryadka neskol'kih chasov.

Etot promezhutok vremeni, konechno, ochen' mal dlya astronomicheskih processov. Odnako v obolochkah novyh zvezd, srazu posle maksimuma bleska, proishodyat stol' bystrye izmeneniya, chto predpolozhenie ob otsutstvii luchevogo ravnovesiya v eto vremya ne yavlyaetsya nepravdopodobnym.

<< 4.3 Rol' stolknovenii i obshego poglosheniya v obolochke | Oglavlenie | Glava V. Zvezdy pozdnih spektral'nyh klassov s yarkimi liniyami >>

Publikacii s klyuchevymi slovami: obolochki zvezd - perenos izlucheniya Publikacii so slovami: obolochki zvezd - perenos izlucheniya
Sm. takzhe: Sbrasyvayushaya massivnuyu obolochku zvezda G79.29+0.46 Obnaruzhenie goryachego vodyanogo para v obolochke uglerodnoi zvezdy. Obolochki v tumannosti Yaico Osveshennost' Planetarnye tumannosti

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

$\sum\limits_1^\infty n_i B_{ic} \rho_{ic} = n_e n^+ \sum\limits_1^\infty C_i ,$	(73)
$\sum\limits_1^\infty n_i B_{ic} \rho_{ic} \epsilon_{ic} = n_e n^+ (\sum\limits_1^\infty C_i \epsilon_i + f),$	(74)

$\sum\limits_1^\infty n_i B_{ic} \rho_{ic}^0 = n_e n^+ \sum\limits_2^\infty C_i ,$	(75)
$\sum\limits_1^\infty n_i B_{ic} \rho_{ic}^0 \epsilon_{ic}^0 = n_e n^+ (\sum\limits_2^\infty C_i \epsilon_i + f),$	(76)