Astronet > Dvizhushiesya obolochki zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Dvizhushiesya obolochki zvezd << Glava V. Zvezdy pozdnih spektral'nyh klassov s yarkimi liniyami | Oglavlenie | 5.2 Opticheskaya tolshina obolochki za granicami subordinatnyh serii >>

5.1 Proishozhdenie "kombinacionnyh spektrov"

Rassmotrim obolochku, okruzhayushuyu goryachuyu zvezdu, prichem budem predpolagat', chto obolochka dvizhetsya. Dlya nachala primenim k etoi obolochke rezul'taty, poluchennye nami v predydushei glave.

My vychislim i sravnim mezhdu soboyu sleduyushie velichiny: 1) energiyu, izluchaemuyu zvezdoi v nepreryvnom spektre, 2) energiyu, izluchaemuyu obolochkoi v nepreryvnom spektre, i 3) energiyu, izluchaemuyu obolochkoi v spektral'nyh liniyah. Eti vychisleniya budut otnosit'sya k vodorodnoi obolochke.

Esli obolochka prozrachna dlya izlucheniya v subordinatnyh seriyah i pogloshaet tol'ko izluchenie ot zvezdy za granicei osnovnoi serii, to, kak izvestno, nepreryvnyi spektr obolochki v vidimoi chasti budet ochen' slab po sravneniyu s nepreryvnym spektrom zvezdy. Vmeste s tem yarkie linii budut ves'ma sil'ny na fone nepreryvnogo spektra obolochki. Takoe polozhenie imeet mesto v gazovyh tumannostyah. Inache obstoit delo v obolochkah malogo radiusa. Eti obolochki pogloshayut izluchenie, idushee ot zvezdy ne tol'ko za granicei osnovnyh serii, no i za granicami subordinatnyh serii. Blagodarya etomu intensivnost' nepreryvnogo spektra obolochek sil'no vozrastaet. Intensivnost' zhe yarkih linii ne ispytyvaet pri etom stol' sil'nogo vozrastaniya iz-za neprozrachnosti obolochki dlya izlucheniya v liniyah. Poetomu pri znachitel'noi neprozrachnosti obolochki dlya: izlucheniya v liniyah (tochnee govorya, pri malyh znacheniyam vvedennogo ranee parametra x) sleduet ozhidat' ves'ma sil'nogo nepreryvnogo spektra obolochki po sravneniyu s nepreryvnym spektrom zvezdy pri sravnitel'noi slabosti yarkih linii. My proverim seichas eti soobrazheniya neposredstvennymi vychisleniyami.

Pust' E_ν^∗ est' energiya, izluchaemaya v chastote ν zvezdoi, i E_ν - energiya, izluchaemaya v chastote v obolochkoi. Eti velichiny opredelyayutsya formulami

$E_{\nu}^* = 4\pi r_*^2 \frac{2h\nu^3}{c^2} \frac{1}{e^{\frac{h\nu}{kT_*}} - 1} ,$ (1)

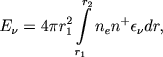
$E_{\nu} = 4\pi r_1^2 \int\limits_{r_1}^{r_2} n_e n^+ \epsilon_{\nu} dr,$ (2)

gde

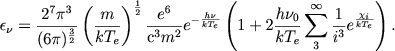
$\epsilon_{\nu} = \frac{2^7 \pi^3}{(6\pi)^{\frac{3}{2}}} \left(\frac{m}{kT_e}\right)^{\frac{1}{2}}\frac{e^6}{s^3 m^2} e^{-\frac{h\nu}{kT_e}}\left(1+2\frac{h\nu_0}{kT_e}\sum\limits_3^\infty \frac{1}{i^3} e^{\frac{\chi_i}{kT_e}}\right).$ (3)

V formule (3) pervyi chlen v skobkah uchityvaet free-free transitions, vtoroi - free-baund transitions. Summirovanie vedetsya nachinaya s i=3, tak kak velichinu E_ν, my predpolagaem vychislit' dlya vidimoi chasti spektra. Pust' dalee E_k2 est' polnaya energiya, izluchaemaya obolochkoi v bal'merovskoi linii, sootvetstvuyushei perehodu k → 2. Eta velichina ravna

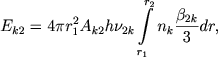
$E_{k2} = 4\pi r_1^2 A_{k2} h\nu_{2k}\int\limits_{r_1}^{r_2} n_k \frac{\beta_{2k}}{3} dr ,$ (4)

gde β_2k/3 est' dolya kvantov, uhodyashih iz obolochki v dannoi linii vsledstvie effekta Doplera.

Dlya vychisleniya integralov (4) i (4) my vospol'zuemsya formulami, opredelyayushimi stepen' vozbuzhdeniya i ionizacii v obolochke, vyvedennymi v predydushei glave. Eti formuly imeyut vid

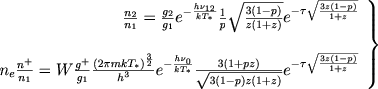
$\left. \begin{array}{r} \frac{n_2}{n_1} = \frac{g_2}{g_1} e^{-\frac{h\nu_{12}}{kT_*}} \frac{1}{p} \sqrt{\frac{3(1-p)}{z(1+z)}} e^{-\tau \sqrt{\frac{3z(1-p)}{1+z}}} \\ \\ n_e \frac{n^+}{n_1} = W\frac{g^+}{g_1} \frac{(2\pi mkT_*)^{\frac{3}{2}}}{h^3} e^{-\frac{h\nu_{0}}{kT_*}} \frac{3(1+pz)}{\sqrt{3(1-p)z(1+z)}} e^{-\tau \sqrt{\frac{3z(1-p)}{1+z}}} \end{array} \right \}$ (5)

gde velichina z svyazana s parametrom x sootnosheniem

$z = \frac{xA_{21}}{pB_{2c} \rho_{2c}^*} ,$ (6)

a parametr x raven

$x=\frac{\beta_{12}}{3W} .$ (7)

Napomnim, chto pri vyvode formul (5) velichina z schitalas' postoyannoi v obolochke.

Vmesto sootnosheniya (2) mozhno napisat'

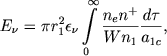
$E_{\nu} = \pi r_1^2 \epsilon_{\nu} \int\limits_{0}^\infty \frac{n_e n^+}{Wn_1} \frac{d\tau}{a_{1c}} ,$ (8)

gde τ - opticheskaya glubina za granicei osnovnoi serii. Podstavlyaya v (8) vtoruyu iz formul (5), poluchaem

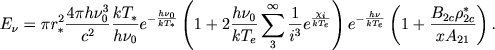
$E_{\nu} = \pi r_*^2 \frac{4\pi h\nu_0^3}{c^2} \frac{kT_*}{h\nu_0} e^{-\frac{h\nu_0}{kT_*}} \left(1+2\frac{h\nu_0}{kT_e} \sum\limits_3^\infty \frac{1}{i^3} e^{\frac{\chi_i}{kT_e}}\right) e^{-\frac{h\nu}{kT_e}} \left(1+\frac{B_{2c} \rho_{2c}^*}{xA_{21}}\right).$ (9)

Otsyuda vidno, chto velichina E_ν sil'no vozrastaet s umen'sheniem parametra h.

Dlya vychisleniya integrala (4) neobhodimo razbit' ego na dva integrala: po oblasti, neprozrachnoi dlya izlucheniya v dannoi linii, i po oblasti, prozrachnoi dlya etogo izlucheniya. Vypolnyaya eto, dlya E_k2 nahodim

$E_{k2} = 4\pi r_1^2 A_{k2} h\nu_{2k} \left[\int\limits_{0}^{\tau_1} n_k \frac{\beta_{2k}}{3} \frac{d\tau}{a_{1c}} + \int\limits_{\tau_1}^\infty n_k \frac{d\tau}{a_{1c}} \right].$ (10)

Etu formulu mozhno preobrazovat' k vidu

$E_{k2} = \pi r_*^2 A_{k2} h\nu_{2k} \left[\frac{n_k}{n_2} x \frac{a_{12}}{a_{2k}} \int\limits_{0}^{\tau_1} \frac{d\tau}{a_{1c}} + \frac{n_k}{n_e n^+} \int\limits_{\tau_1}^\infty \frac{n_e n^+}{Wn_1} \frac{d\tau}{a_{1c}} \right].$ (11)

Integriruya i pol'zuyas' tem, chto pri τ = τ₁ dolzhno byt'

$\frac{n_k}{n_2} x \frac{a_{12}}{a_{2k}} = \frac{n_k}{n_e n^+} \frac{n_e n^+}{Wn_1} ,$ (12)

vmesto (1) poluchaem

$E_{k2} = \pi r_*^2 \frac{A_{k2} h\nu_{2k}}{a_{1c}} \frac{n_k}{n_2} x \frac{a_{12}}{a_{2k}} \left[\tau_1 + \sqrt{\frac{1+z}{3(1-p)z}}\right].$ (13)

Vhodyashaya v etu formulu velichina τ₁, t. e. granichnoe znachenie mezhdu dvumya upomyanutymi oblastyami, opredelyaetsya sootnosheniem (12). S pomosh'yu pervoi iz formul (5) iz etogo sootnosheniya nahodim

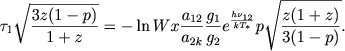
$\tau_1 \sqrt{\frac{3z(1-p)}{1+z}} = -\ln W x \frac{a_{12}}{a_{2k}} \frac{g_1}{g_2} e^{\frac{h\nu_{12}}{kT_*}} p \sqrt{\frac{z(1+z)}{3(1-p)}} .$ (14)

Podstavlyaya (14) v (13), okonchatel'no poluchaem

$E_{k2} = \left[ -\ln W x \frac{a_{12}}{a_{2k}} \frac{g_1}{g_2} e^{\frac{h\nu_{12}}{kT_*}} p \sqrt{\frac{z(1+z)}{3(1-p)}} +1 \right] \pi r_*^2 \frac{A_{k2} h\nu_{2k}}{a_{1c}} \frac{n_k}{n_2} x \frac{a_{12}}{a_{2k}} \sqrt{\frac{1+z}{3(1-p)z}} .$ (15)

Etoi formuloi my i budem pol'zovat'sya dlya vychisleniya polnoi energii, izluchaemoi obolochkoi v dannoi linii.

Sravnim teper' mezhdu soboyu tol'ko chto opredelennye velichiny E^*_ν, E_ν i E_k2 Dlya harakteristiki otnosheniya energii v linii k energii, izluchaemoi obolochkoi v nepreryvnom spektre, my vospol'zuemsya zanstrovskimi velichinami A_k, ravnymi

$A_k = \frac{E_{k2}}{\nu_{2k} {E^*_\nu}} .$ (16)

S pomosh'yu vysheprivedennyh formul (1), (9) i (15) my sostavili tablicy XIV i XV, v kotoryh dlya raznyh znachenii parametra h dany znacheniya velichin A_β i E_ν/E^*_ν v oblsti linii H_β. Pervaya iz etih tablic otnositsya k sluchayu T_∗=20000°; ,T_e=20000°;, vtoraya k sluchayu (T_∗=50000°; ,T_e=20000°;). Neobhodimye dlya vychislenii znacheniya velichin n₄/n₂ byli vzyaty iz tablic II i III glavy I. Dlya W bylo prinyato znachenie W=10^-4. Chetvertaya strochka kazhdoi iz tablic daet otnoshenie energii, izluchaemoi v linii H_β neprozrachnoi chast'yu obolochki, k energii, izluchaemoi i toi zhe linii prozrachnoi chast'yu obolochki. V pyatoi strochke dany znacheniya opticheskoi tolshiny obolochki za granicei bal'merovskoi serii. Eta velichina vychislyalas' po formule

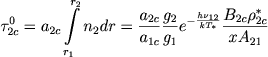
$\tau_{2c}^0 = a_{2c}\int\limits_{r_1}^{r_2} n_2 dr = \frac{a_{2c}}{a_{1c}} \frac{g_2}{g_1} e^{-\frac{h\nu_{12}}{kT_*}} \frac{B_{2c} \rho_{2c}^*}{x A_{21}}$ (17)

(ob etoi velichine sm. nizhe).

Tablica XIV
(T_∗=20000°; ,T_e=20000°;)

x 0,01 0,001 0,0001

E_ν/E^∗_ν 0,03 0,24 2,1

A_β 0,42 0,03 0,002

$\tau_1 \sqrt{\frac{3z(1-p)}{1+z}}$ 10 14 17

τ_2c⁰ 0,06 0,6 6,0

Tablica XV
(T_∗=50000°; ,T_e=20000°;)

x 1 0,1 0,01

E_ν/E^∗_ν 0,6 1,6 11,5

A_β 0,35 0,045 0,002

$\tau_1 \sqrt{\frac{3z(1-p)}{1+z}}$ 7 7 7

τ_2c⁰ 0,16 1,6 16

Iz rassmotreniya privedennyh tablic my mozhem sdelat' sleduyushii vyvod. S umen'sheniem parametra h velichina E_ν/E^∗_ν vozrastaet, a velichina A_β ubyvaet. Pri dostatochno malyh znacheniyah h nepreryvnyi spektr obolochki stanovitsya yarche nepreryvnogo spektra zvezdy, a velichina A_β stanovitsya blizkoi k svoim nablyudaemym v zvezdnyh spektrah znacheniyam (poryadka 0,001).

Iz obshih fizicheskih principov sleduet, chto izluchenie obolochki v nepreryvnom spektre dolzhno sootvetstvovat' temperature bolee nizkoi, chem temperatura zvezdy. Eto vidno i iz formuly (9), dayushei raspredelenie energii v nepreryvnom spektre obolochki. Naidem, naprimer, cvetovuyu temperaturu obolochki v vidimoi chasti spektra. Iz formuly (9) vytekaet, chto

$E_\nu \sim e^{-\frac{h\nu}{kT_*}} .$ (18)

Obychno zhe schitaetsya, chto raspredelenie energii v nepreryvnom spektre opisyvaetsya formuloi Planka s nekotoroi temperaturoi T'

$E_\nu \sim \frac{\nu^3}{e^{\frac{h\nu}{kT^\prime}} -1} .$ (19)

Legko videt', chto temperatury T' i T_e svyazany drug s drugom sootnosheniem

$\frac{h\nu}{k}\left(\frac{1}{T^\prime} - \frac{1}{T_e}\right) = 3 .$ (20)

V oblasti linii H_β vmesto (20) imeem

$10000\left(\frac{1}{T^\prime} - \frac{1}{T_e}\right) = 1 .$ (21)

Eto znachit, chto temperatura T' gorazdo men'she temperatury T_e. Tak, naprimer, pri T_e = 20000°; dlya T' poluchaem T' = 6700°; . Poetomu izluchenie obolochki dazhe pri ochen' vysokoi temperature T_e budet kazat'sya nizkotemperaturnym.

Otmetim, chto raspredelenie energii v spektrah zvezd pozdnih klassov s yarkimi liniyami iz-za slozhnogo absorbcionnogo spektra izvestno ploho. Dlya zvezdy Z Andromedae Plaskett poluchil T' = 5200°; ± 900°; . Nesomnenno, odnako, chto cvetovye temperatury dolgoperiodicheskih peremennyh znachitel'no nizhe privedennogo znacheniya, ibo eti zvezdy ves'ma "krasnye".

Dlya ob'yasneniya sil'nogo pokrasneniya obolochki po sravneniyu s zvezdoi sleduet imet' v vidu, chto nashi rezul'taty, privedennye vyshe, ne vpolne pravil'ny. Delo v tom, chto pri vyvode formul (5), opredelyayushih vozbuzhdenie i ionizaciyu v obolochke, my schitali, chto opticheskaya tolshina obolochki za granicami subordinatnyh serii men'she edinicy. Na samom dele, kak vidno iz tablic XIV i XV, s umen'sheniem parametra h velichina τ_2c⁰ vozrastaet i pri dostatochno malyh znacheniyah h stanovitsya τ_2c⁰ > 1. V etom poslednem sluchae teoriya luchevogo ravnovesiya delaetsya ves'ma slozhnoi, i podrobnoe rassmotrenie etogo sluchaya vyhodit za ramki nastoyashei raboty. Odnako vpolne ochevidnym yavlyaetsya sleduyushee. Esli τ_1c⁰ >> 1, no τ_2c⁰ < 1, to obolochka polnost'yu pogloshaet izluchenie zvezdy za granicei osnovnoi serii, chastichno pogloshaet izluchenie zvezdy za granicami subordinatnyh serii i izluchaet energiyu za granicami subordinatnyh serii i v spektral'nyh liniyah. Kvanty zhe za granicei osnovnoi serii, izluchennye obolochkoi, snova pogloshayutsya v obolochke, i eto prodolzhaetsya do teh por, poka pochti vse eti kvanty ne budut pererabotany v kvanty bolee nizkih chastot. Etot sluchai byl rassmotren vyshe i privel k formule (9), opredelyayushei izluchenie obolochki v nepreryvnom spektre. Esli zhe tol'ko τ_1c⁰ >> 1, no i τ_2c⁰ > 1, to obolochka pererabatyvaet v izluchenie nizkih chastot ne tol'ko izluchenie za granicei osnovnoi serii, no i izluchenie za granicami subordinatnyh serii. Samo soboyu razumeetsya, chto eto otnositsya kak k izlucheniyu, idushemu ot zvezdy, tak i k sobstvennomu izlucheniyu obolochki. Yasno, chto izluchenie obolochki vo vtorom sluchae budet sootvetstvovat' eshe bolee nizkoi temperature, chem v pervom. Takovo v obshih chertah proishozhdenie nepreryvnogo spektra pozdnego tipa, izluchaemogo obolochkoi.

Kak bylo vyyasneno vyshe, vid spektra obolochki sushestvenno zavisit ot parametra h, ravnogo

$x = \frac{1}{3W}\frac{1}{2u} \frac{dv}{n_1 a_{12} dr} .$ (22)

Soglasno zhe ionizacionnoi formule, Wn₁ ∼ n_en⁺. Eto znachit, chto parametr h tem men'she, chem bol'she plotnost' obolochki. Poetomu my prihodim k zaklyucheniyu, chto pri prochih ravnyh usloviyah (t. e. pri odinakovyh znacheniyah temperatury central'noi zvezdy, koefficienta dilyucii i t. d.) nepreryvnyi spektr obolochki budet tem bolee pozdnim, chem bol'she plotnost' obolochki.

Nam eshe ostaetsya ob'yasnit' proishozhdenie absorbcionnogo spektra pozdnego tipa. Dlya etogo obratimsya k polozheniyu del vo vneshnih chastyah obolochki. Pri dostatochno malyh znacheniyah parametra h vnutrennyaya, chast' obolochki polnost'yu ekraniruet vysokochastotnoe izluchenie, idushee ot zvezdy. Poetomu vneshnyaya chast' obolochki nahoditsya pod vozdeistviem nizkotemperaturnogo izlucheniya samoi obolochki. Sledovatel'no, v etih chastyah vozbuzhdenie i ionizaciya atomov dolzhny sootvetstvovat' ves'ma nizkoi temperature. Drugimi slovami, zdes' dolzhny sushestvovat' neionizovannye atomy metallov i molekulyarnye soedineniya. Imenno vo vneshnih chastyah obolochki i voznikaet absorbcionnyi spektr pozdnego tipa.

Takim obrazom my prihodim k sleduyushemu vyvodu. Vnutrennyaya chast' obolochki igraet rol' "fotosfery", sozdavaya nepreryvnyi spektr pozdnego tipa. Vo vneshnei chasti obolochki, igrayushei rol' "atmosfery", voznikayut absorbcionnye linii neionizovannyh metallov i molekulyarnye polosy. V sloe, neposredstvenno prilegayushem k "fotosfere", voznikayut emissionnye linii vodoroda i ionizovannyh metallov. Pri dostatochno vysokoi temperature zvezdy v spektre dolzhny nablyudat'sya takzhe emissionnye linii atomov s ochen' vysokim potencialom ionizacii.

Sleduet podcherknut', chto dlya nashih vyvodov sushestvenno, chtoby opticheskaya tolshina obolochki za granicami subordinatnyh serii byla bol'she edinicy. Poetomu my dolzhny podrobno rassmotret' prichiny, vliyayushie na velichinu τ_2c⁰. Etomu voprosu posvyashaetsya sleduyushii paragraf.

<< Glava V. Zvezdy pozdnih spektral'nyh klassov s yarkimi liniyami | Oglavlenie | 5.2 Opticheskaya tolshina obolochki za granicami subordinatnyh serii >>

Publikacii s klyuchevymi slovami: obolochki zvezd - perenos izlucheniya Publikacii so slovami: obolochki zvezd - perenos izlucheniya
Sm. takzhe: Sbrasyvayushaya massivnuyu obolochku zvezda G79.29+0.46 Obnaruzhenie goryachego vodyanogo para v obolochke uglerodnoi zvezdy. Obolochki v tumannosti Yaico Osveshennost' Planetarnye tumannosti

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

$E_{\nu}^* = 4\pi r_^2 \frac{2h\nu^3}{c^2} \frac{1}{e^{\frac{h\nu}{kT_}} - 1} ,$	(1)
$E_{\nu} = 4\pi r_1^2 \int\limits_{r_1}^{r_2} n_e n^+ \epsilon_{\nu} dr,$	(2)

x	0,01	0,001	0,0001
E_ν/E^∗_ν	0,03	0,24	2,1
A_β	0,42	0,03	0,002
$\tau_1 \sqrt{\frac{3z(1-p)}{1+z}}$	10	14	17
τ_2c⁰	0,06	0,6	6,0

x	1	0,1	0,01
E_ν/E^∗_ν	0,6	1,6	11,5
A_β	0,35	0,045	0,002
$\tau_1 \sqrt{\frac{3z(1-p)}{1+z}}$	7	7	7
τ_2c⁰	0,16	1,6	16