Astronet > Dvizhushiesya obolochki zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Dvizhushiesya obolochki zvezd << 5.1 Proishozhdenie "kombinacionnyh spektrov" | Oglavlenie | 5.3 Obshie soobrazheniya >>

5.2 Opticheskaya tolshina obolochki za granicami subordinatnyh serii

V predydushei glave byli ukazany tri prichiny, ponizhayushie stepen' vozbuzhdeniya i ionizacii v obolochke: 1) effekt Doplera, 2) udary vtorogo roda i 3) nalichie obshego poglosheniya. Pri vyvode formul (5) byl uchten tol'ko effekt Dopplera. Teper' my primem vo vnimanie dve drugie prichiny.

Tret'ya iz etih prichin s pervogo vzglyada kazhetsya osobenno "opasnoi". Sleduet, odnako, imet' v vidu, chto v rassmatrivaemom sluchae obshee pogloshenie v obolochke est' ne chto inoe, kak pogloshenie za granicei subordinatnoi serii dannogo atoma, a eto pogloshenie ubyvaet s ponizheniem stepeni vozbuzhdeniya i ionizacii. Sledovatel'no, v etom sluchae stepen' vozbuzhdeniya i ionizacii budet padat' medlennee, chem eto bylo polucheno v predydushei glave (§ 3, b).

My snova dopustim, chto atom obladaet tol'ko tremya urovnyami, i budem ishodit' iz uravnenii (IV, 62). Prenebregaya ochen' maloi velichinoi η₁ i uchityvaya stolknoveniya, vmesto etih uravnenii poluchaem

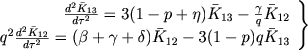
$\left. \begin{array}{r} \frac{d^2 \bar K_{13}}{d\tau^2} = 3(1 - p + \eta)\bar K_{13} - \frac{\gamma}{q} \bar K_{12} \\ q^2 \frac{d^2 \bar K_{12}}{d\tau^2} = (\beta + \gamma + \delta)\bar K_{12} - 3(1-p)q\bar K_{13} \end{array} \right \}$ (23)

Dlya chastei obolochki, dostatochno udalennyh ot granic, otsyuda nahodim

$\frac{d^2 \bar K_{13}}{d\tau^2} = 3\left[\eta + (1-p) \frac{\beta + \gamma}{\beta + \gamma + \delta} \right]\bar K_{13}.$ (24)

Vhodyashaya v eto uravnenie velichina η opredelyaetsya pervym iz ravenstv (IV, 61). Oboznachaya cherez μ. otnoshenie koefficienta poglosheniya za granicei osnovnoi serii, vyzvannogo perehodami tipa 2 → 3, k koefficientu poglosheniya za granicei subordinatnoi serii (μ = a'₁₃/a₂₃), i imeya v vidu sootnoshenie

$\frac{a_{23}}{a_{13}} = \frac{1-p}{p}\frac{\bar K_{13}}{\bar K_{23}} .$ (25)

dlya velichiny η imeem

$\eta = \mu \frac{1-p}{p}\frac{\bar K_{13}}{\bar K_{23}} .$ (26)

No $\bar K_{13} = \frac{1}{4} S_{23}$ . Poetomu, podstavlyaya (26) v (24), poluchaem

$\frac{d^2 \bar K_{13}}{d\tau^2} = 3\left[4\mu \frac{1-p}{pS_{23}} \bar K_{13} + (1-p) \frac{\beta + \gamma}{\beta + \gamma + \delta} \right]\bar K_{13}.$ (27)

Reshenie uravneniya (27) poluchaetsya v vide ellipticheskogo integrala

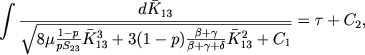
$\int\frac{d\bar K_{13}}{\sqrt{8\mu \frac{1-p}{pS_{23}} \bar K_{13}^3 + 3(1-p) \frac{\beta + \gamma}{\beta + \gamma + \delta} \bar K_{13}^2 + C_1}} = \tau + C_2 ,$ (28)

gde C₁ i C₂ - proizvol'nye postoyannye. Eti postoyannye dolzhny byt' opredeleny iz granichnyh uslovii:

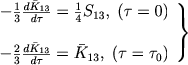
$\left. \begin{array}{r} -\frac{1}{3} \frac{d\bar K_{13}}{d\tau} = \frac{1}{4}S_{13}, \;(\tau = 0) \\ \\ -\frac{2}{3} \frac{d\bar K_{13}}{d\tau} = \bar K_{13}, \;(\tau = \tau_0) \end{array} \right \}$ (29)

Esli obshee pogloshenie v obolochke igraet ból'shuyu rol', chem effekt Doplera i stolknoveniya, to reshenie uravneniya (27) pri granichnyh usloviyah (29) dlya sluchaya τ₀=∞ imeet vid

$\bar K_{13} = \frac{\frac{3}{4} S_{13}}{\mu\tau_{23}^0 \left(1+\frac{\mu}{2} \tau_{23}^0 \tau \right)} ,$ (30)

gde τ₂₃⁰ est' opticheskaya tolshina obolochki za granicei subordinatnoi seriyu. Eta tolshina okazyvaetsya ravnoi

$\tau_{23}^0 = \left(6 \frac{1-p}{p\mu^2}\frac{S_{13}}{S_{23}}\right)^{\frac{1}{3}} .$ (31)

V protivopolozhnom sluchae reshenie uravneniya (27) poluchaetsya v forme, poluchennoi nami ranee [sm. pervuyu iz formul (IV, 32)], a imenno:

$\bar K_{13} = \frac{3S_{13}}{4\lambda} e^{-\lambda\tau} ,$ (32)

gde

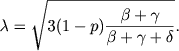
$\lambda = \sqrt{3(1-p) \frac{\beta + \gamma}{\beta + \gamma + \delta}} .$ (33)

Dlya velichiny τ₂₃⁰ v etom sluchae nahodim

$\tau_{23}^0 = 3 \frac{1-p}{p\lambda^2}\frac{S_{13}}{S_{23}} .$ (34)

Ocenim teper' poluchennye vyrazheniya dlya τ₂₃⁰. Dlya vodorodnogo atoma p=1/2, μ=1/64. Poetomu pri temperature zvezdy poryadka T_∗=30000°; formula (31) daet dlya τ₂₃⁰, velichinu poryadka neskol'kih desyatkov. Pri W = 10^-4, n_e = 10¹¹ i β < 10^-6 formula (34) daet dlya τ₂₃⁰, velichinu togo zhe poryadka. My vidim, sledovatel'no, chto uchet stolknovenii i obshego poglosheniya ne ponizhaet znachitel'no opticheskoi tolshiny obolochki za granicei subordinatnoi serii.

Dannoe nami reshenie zadachi yavlyaetsya, odnako, ne vpolne tochnym, tak kak pri τ₂₃⁰ > 1, velichinu $\bar K_{23}$ nel'zya schitat' postoyannoi. No legko videt', chto v chastote ν₂₃ my imeem po sushestvu chistoe rasseyanie. Eto znachit, chto velichina $\bar K_{23}$ ne mozhet sil'no menyat'sya v obolochke. Poetomu i tochnoe reshenie zadachi ne mozhet privesti k rezul'tatam, znachitel'no otlichayushimsya ot tol'ko chto poluchennyh. My seichas dadim eto tochnoe reshenie zadachi, dlya prostoty prenebregaya stolknoveniyami i effektom Doplera.

Vmesto odnogo uravneniya (27) my teper' imeem sleduyushuyu sistemu treh uravnenii:

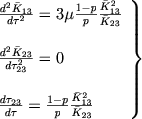
$\left. \begin{array}{l} \frac{d^2 \bar K_{13}}{d\tau^2} = 3\mu \frac{1 - p}{p} \frac{\bar K_{13}^2}{\bar K_{23}} \\ \\ \frac{d^2 \bar K_{23}}{d\tau_{23}^2} = 0 \\ \\ \frac{d\tau_{23}}{d\tau} = \frac{1 - p}{p} \frac{\bar K_{13}^2}{\bar K_{23}} \end{array} \right \}$ (35)

Vtoroe iz etih uravnenii pri granichnyh usloviyah analogichnyh (29), daet

$\bar K_{23} = \frac{3}{4} S_{23}(\tau_{23}^0 - \tau_{23}) ,$ (36)

iz tret'ego uravneniya nahodim

$\bar K_{13} = -\frac{4p}{3(1-p)} \frac{\bar K_{23}}{S_{23}} \frac{d \bar K_{23}}{d\tau} ,$ (37)

Podstavlyaya (37) v pervoe iz uravnenii (35), poluchaem

$\frac{d^2}{d\tau^2}\left(\bar K_{23} \frac{d \bar K_{23}}{d\tau}\right) = -\frac{4\mu}{S_{23}} \bar K_{23} \left(\frac{d \bar K_{23}}{d\tau}\right)^2 .$ (38)

Eto slozhnoe na vid uravnenie imeet sleduyushee prostoe reshenie:

$\bar K_{23} = \frac{\frac{3}{4} S_2^0 \tau_{23}^0}{1+\frac{\mu}{4} \tau_{23}^0 \tau} ,$ (39)

udovletvoryayushee tem zhe samym granichnym usloviyam (tak kak dolzhno byt': τ₂₃ = 0 pri τ = 0 i τ₂₃ = τ₂₃⁰ pri τ = ∞). Podstavlyaya (39)) v (37) i ispol'zuya uslovie (29) dlya opredeleniya postoyannoi τ₂₃⁰, okonchatel'no nahodim

$\bar K_{13} = \frac{S_{13}}{\mu\tau_{23}^0} \frac{1}{\left(1+\frac{\mu}{4} \tau_{23}^0 \tau \right)^3} ,$ (40)

$\tau_{23}^0 = \left(\frac{16}{3} \frac{1-p}{p\mu^2}\frac{S_{13}}{S_{23}}\right)^{\frac{1}{4}} .$ (41)

My deistvitel'no vidim, chto tochnoe reshenie zadachi, davaemoe formulami (40) i (41), ochen' malo otlichaetsya ot ranee poluchennogo resheniya, davaemogo formulami (30) i (31).

V zaklyuchenie sleduet zametit', chto vyshe byli uchteny tol'ko faktory, okazyvayushie ponizhayushee deistvie na stepen' vozbuzhdeniya i ionizacii v obolochke. Sushestvuyut, odnako, faktory, deistvuyushie obratnym obrazom (naprimer udary pervogo roda). Poetomu privedennye vyshe ocenki velichiny τ₂₃⁰ yavlyayutsya na samom dele minimal'nymi.

<< 5.1 Proishozhdenie "kombinacionnyh spektrov" | Oglavlenie | 5.3 Obshie soobrazheniya >>

Publikacii s klyuchevymi slovami: obolochki zvezd - perenos izlucheniya Publikacii so slovami: obolochki zvezd - perenos izlucheniya
Sm. takzhe: Sbrasyvayushaya massivnuyu obolochku zvezda G79.29+0.46 Obnaruzhenie goryachego vodyanogo para v obolochke uglerodnoi zvezdy. Obolochki v tumannosti Yaico Osveshennost' Planetarnye tumannosti

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

$\bar K_{13} = \frac{S_{13}}{\mu\tau_{23}^0} \frac{1}{\left(1+\frac{\mu}{4} \tau_{23}^0 \tau \right)^3} ,$	(40)
$\tau_{23}^0 = \left(\frac{16}{3} \frac{1-p}{p\mu^2}\frac{S_{13}}{S_{23}}\right)^{\frac{1}{4}} .$	(41)