10.1 Formuly Botlingera

Lekciya 10. Vrashenie Galaktiki

10.1 Formuly Botlingera

Rassmotrim neslozhnuyu kinematicheskuyu model' Galaktiki, sdelav uproshayushee predpolozhenie, chto centroidy dvizhutsya vokrug centra Galaktiki po krugovym orbitam. Dvizhenie osushestvlyaetsya vokrug osi simmetrii Galaktiki v ploskostyah, parallel'nyh osnovnoi ploskosti simmetrii Galaktiki. Pri etom v kazhdoi iz parallel'nyh ploskostei vrashenie proishodit odinakovo, t.e. funkcii, opisyvayushie vrashenie Galaktiki ne zavisyat ot z. Takoi tip dvizheniya nazyvaetsya barotropnym vrasheniem. Pri etom na zakon vrasheniya - zavisimost' skorosti vrasheniya ot rasstoyaniya do osi vrasheniya Galaktiki - nikakih ogranichenii ne nakladyvaetsya. Vyvedem formuly, opisyvayushie nablyudaemye proyavleniya vrasheniya Galaktiki pri sdelannyh predpolozheniyah, sleduya Botlingeru.

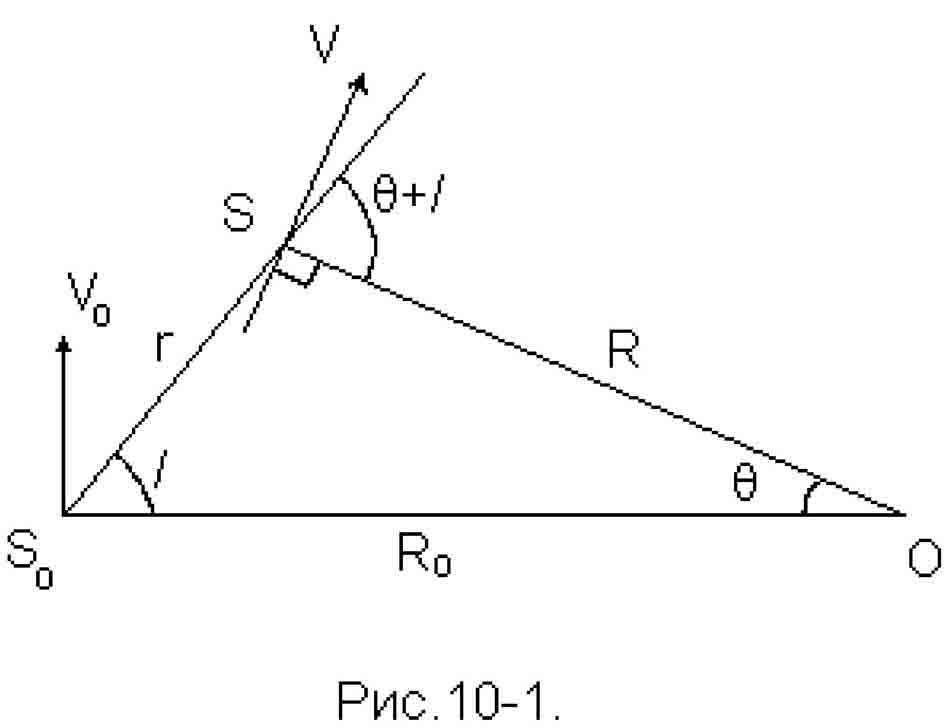
Rassmotrim ob'ekt S, lezhashii v ploskosti Galaktiki (sm. ris. 10-1). Vektor V₀ predstavlyaet soboi lineinuyu skorost' krugovogo dvizheniya centroida S₀ zvezd, vmeste s Solncem obrashayushegosya vokrug centra Galaktiki na rasstoyanii R₀ ot osi ee vrasheniya. Vektor V - krugovaya skorost' centroida S, nahodyashegosya na rasstoyanii r ot centroida S₀ i harakterizuemogo galakticheskoi dolgotoi l. Soglasno prinyatoi modeli vektory V i V₀ napravleny po kasatel'nym k okruzhnostyam s radiusami R i R₀. Uglovye skorosti krugovogo dvizheniya na rasstoyaniyah R i R₀ ot osi vrasheniya Galaktiki budut: Naidem proekcii vektorov V i V₀ na luch zreniya S₀S. Oni, sootvetstvenno, ravny V cos[90° - (Θ + l)] i V₀ cos (90° - l) i ili, ispol'zuya (10-1), ωR sin(Θ + l) i ω₀R₀ sin l. Raznost' etih dvuh velichin - sostavlyayushaya luchevoi skorosti, otrazhayushaya differencial'noe vrashenie Galaktiki: Vospol'zuemsya teoremoi sinusov dlya treugol'nika S₀OS : otkuda poluchim: Podstaviv sinus summy uglov iz (10-4) v vyrazhenie (10-2) poluchim formulu Botlingera dlya luchevyh skorostei: gde mnozhitel' cosb vveden dlya ucheta galakticheskoi shiroty, tak kak R est' rasstoyanie tochki S ot osi vrasheniya, a ne ot centra Galaktiki.

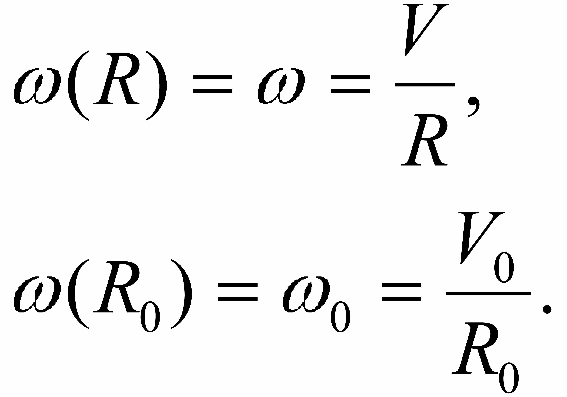
Analogichno mozhno vyvesti formulu dlya tangencial'noi skorosti v_l = 4.74 rμ_l cos b: Mozhno takzhe vyvesti podobnoe vyrazhenie i dlya v_b = 4.74 rμ_b cos b , odnako obychno formuly Botlingera primenyayutsya dlya ob'ektov, lezhashih vblizi ploskosti Galaktiki, dlya kotoryh etot komponent tangencial'noi skorosti soderzhit malyi vklad ot vrasheniya Galaktiki. Poetomu formula dlya v_l v issledovaniyah ne primenyaetsya.

Napomnim, chto v (10-5) i (10-6) chastota vrasheniya Galaktiki, chasto nazyvaemaya krivoi vrasheniya Galaktiki, yavlyaetsya funkciei rasstoyaniya ot osi vrasheniya Galaktiki R. Vyrazheniya (10-5) i (10-6) yavlyayutsya osnovnymi formulami, primenyaemymi pri issledovanii kinematicheskih svoistv galakticheskogo diska. Otmetim, chto takoi vazhnyi parametr galakticheskogo vrasheniya, kak chastota vrasheniya Galaktiki na rasstoyanii Solnca μ₀, mozhet byt' opredelen tol'ko s ispol'zovaniem sobstvennyh dvizhenii iz vyrazheniya (10-6), togda kak s pomosh'yu luchevyh skorostei krivaya vrasheniya opredelyaetsya tol'ko s tochnost'yu do postoyannogo slagaemogo ω₀. Poetomu tochnost' opredeleniya chastoty vrasheniya Galaktiki celikom opredelyaetsya tochnost'yu sistemy, ispol'zuemoi dlya ocenki sobstvennyh dvizhenii.

Publikacii s klyuchevymi slovami: zvezdnaya astronomiya Publikacii so slovami: zvezdnaya astronomiya
Sm. takzhe: Elene Vyacheslavovne Glushkovoi - 50 ! Konferenciya «Sovremennaya zvezdnaya astronomiya - 2014» Konferenciya "Sovremennaya zvezdnaya astronomiya" K 100-letiyu so dnya rozhdeniya Petra Grigor'evicha Kulikovskogo Lekcii po Galakticheskoi Astronomii. 5–8 Lekcii po Galakticheskoi Astronomii. 3–4 Lekcii po Galakticheskoi Astronomii. 1–2 Vse publikacii na tu zhe temu >>