10.5 Krivaya vrasheniya Galaktiki

Lekciya 10. Vrashenie Galaktiki

10.5 Krivaya vrasheniya Galaktiki

Poluchenie krivoi vrasheniya Galaktiki - glavnaya cel' kinematicheskih issledovanii Galaktiki. Ona interesna ne tol'ko sama po sebe kak funkciya, opisyvayushaya kinematicheskie svoistva Galaktiki. Ona, prezhde vsego, vazhna tem, chto soderzhit informaciyu o raspredelenii materii v Galaktike. Deistvitel'no, krugovaya skorost' mozhet byt' opredelena iz ravenstva sily tyagoteniya centrostremitel'noi sile, uderzhivayushei telo na krugovoi orbite: gde F = F(R,z) est' gravitacionnyi potencial Galaktiki. Zdes' my prinyali dlya prostoty izlozheniya, chto Galaktika yavlyaetsya obrazovaniem, obladayushim cilindricheskoi simmetriei, t.e. yavlyaetsya telom vrasheniya. Vmeste s tem my znaem, chto raspredelenie plotnosti materii podchinyaetsya uravneniyu Puassona: gde ρ(R,z) est' plotnost' veshestva, G - gravitacionnaya postoyannaya. Dva poslednih vyrazheniya pokazyvayut, chto krivaya krugovyh skorostei, kotoruyu my otozhdestvlyaem s krivoi vrasheniya Galaktiki, soderzhit vazhnuyu informaciyu o raspredelenii veshestva v Galaktike. Klyuchevym voprosom pri etom yavlyaetsya tochnost' vypolneniya gipotezy o ravenstve nablyudaemoi krivoi vrasheniya i krivoi krugovyh skorostei. Odnako malost' dispersii ostatochnyh skorostei ob'ektov tonkogo diska Galaktiki - molodyh rasseyannyh skoplenii, OV-zvezd i klassicheskih cefeid - po sravneniyu so skorost'yu vrasheniya galakticheskogo diska pozvolyaet nadeyat'sya, chto eta gipoteza vypolnyaetsya s bol'shoi tochnost'yu.

Kakoi mozhet byt' krivaya vrasheniya nashei Galaktiki? Mozhno rassmotret' dva predel'nyh sluchaya. Pervyi - eto tverdotel'noe vrashenie, kogda pri lyubom rasstoyanii ot centra Galaktiki R uglovaya skorost' vrasheniya odinakova, a lineinaya skorost' vozrastaet proporcional'no R. Vtoroi - eto keplerovskoe vrashenie, kogda vsya massa Galaktiki sosredotochena v ee centre. V etom sluchae my imeem ubyvayushuyu krivuyu lineinyh skorostei, proporcional'nuyu R^-1/2.

Pereidem teper' k sposobam opredeleniya krivoi vrasheniya iz nablyudatel'nyh dannyh. Vnov' obratimsya k formule Botlingera dlya luchevyh skorostei: Razdelim obe chasti ravenstva na Poluchim: Funkciya f(R,R₀) , stoyashaya v levoi chasti ravenstva, obychno nazyvaetsya funkciei Kamma po imeni issledovatelya, vpervye primenivshego etu funkciyu dlya issledovaniya differencial'nogo vrasheniya Galaktiki. Inogda etu funkciyu nazyvayut funkciei Kamma-Parenago, tak kak Parenago v 1941g. nezavisimo ot Kamma primenyal formulu (10-25) dlya issledovaniya vrasheniya Galaktiki. Vyrazhenie (10-25) pokazyvaet, chto funkciya Kamma tol'ko na postoyannoe slagaemoe otlichaetsya ot krivoi uglovoi skorosti vrasheniya i daet zavisimost' chastoty vrasheniya ot rasstoyaniya ot osi vrasheniya Galaktiki.

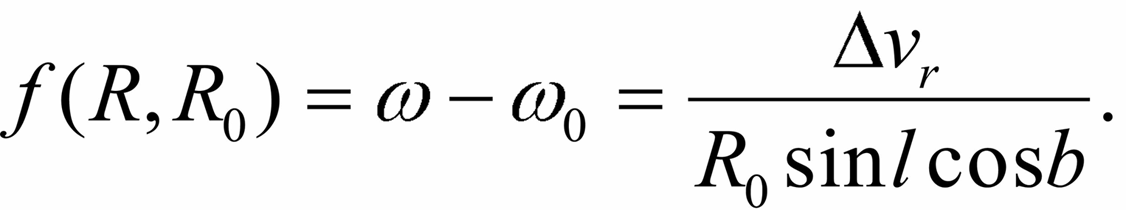
Primenenie metoda Kamma mozhno razbit' na sleduyushie etapy:

• - opredelenie dlya izbrannoi gruppy ob'ektov individual'nyh rasstoyanii r, ispravlennyh za mezhzvezdnoe pogloshenie;
• - vychislenie rasstoyaniya ot osi vrasheniya Galaktiki R dlya kazhdogo iz ob'ektov po teoreme kosinusov:
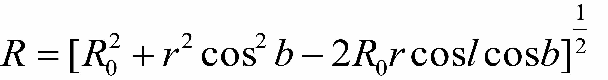
• - opredelenie ω - ω₀ dlya kazhdogo iz ob'ektov;
• - esli ob'ektov v vyborke mnogo, to - usrednenie funkcii Kamma v podhodyashih intervalah R i postroenie grafika kak funkcii R.

Otmetim poputno, chto podhodyashim obrazom sglazhennaya funkciya Kamma mozhet sluzhit' dlya opredeleniya postoyannoi Oorta A putem chislennogo differencirovaniya, chto yavlyaetsya bolee obosnovannym metodom polucheniya ocenki postoyannoi Oorta, tak kak ocenivanie po formule (10-13) pozvolyaet opredelit' etu velichinu lish' kak koefficient priblizhayushego nablyudaemoe pole skorostei polinoma.

V § 10.4 bylo pokazano, kak po nablyudatel'nym dannym mozhno ocenit' chastotu vrasheniya Galaktiki na kruge Solnca . Esli dobavit' k funkcii Kamma etu velichinu, a zatem kazhduyu tochku umnozhit' na sootvetstvuyushee znachenie R, my poluchim krivuyu differencial'nogo vrasheniya Galaktiki v vide krivoi lineinyh skorostei vrasheniya. Krivaya lineinyh skorostei gorazdo bolee naglyadna i udobna dlya issledovaniya. Na ris.10-3 svedeny rezul'taty issledovanii poslednih let, gde krivaya vrasheniya opredelena po samym raznym ob'ektam - po radioizlucheniyu neitral'nogo vodoroda i molekulyarnyh oblakov, po luchevym skorostyam rasseyannyh skoplenii i klassicheskih cefeid i t.d. V kachestve ordinaty ispol'zovano galaktocentricheskoe rasstoyanie v edinicah rasstoyaniya Solnca ot centra Galaktiki R₀. Kak mozhno videt' iz risunka, krivaya vrasheniya nashei Galaktiki bolee-menee nadezhno opredelena do galaktocentricheskogo rasstoyaniya primerno 12 kpk (nami prinyato R₀ = 8 kpk). Chto delaetsya za etim predelom ne vpolne yasno, odnako, pohozhe, chto maksimum krivoi vrasheniya poka ne dostigaetsya. Vprochem, v etoi oblasti ochen' veliki oshibki opredeleniya krivoi vrasheniya i dlya uverennyh vyvodov trebuyutsya dal'neishie issledovaniya.

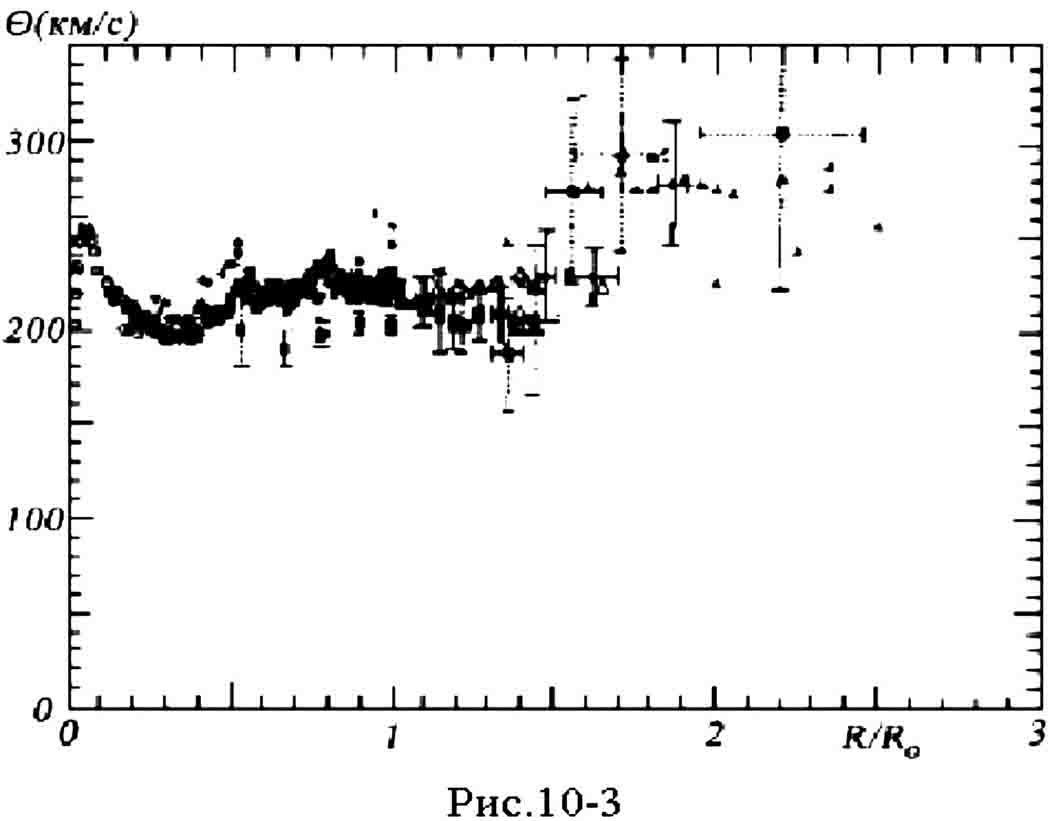Harakternymi osobennostyami krivoi vrasheniya, vydelyayushimisya na ris. 10-3, yavlyayutsya rezkii minimum vblizi galakticheskogo centra, ostryi maksimum na rasstoyanii okolo 1 kpk ot centra, zatem vtorichnyi minimum i vnov' nebol'shoi maksimum, posle kotorogo nablyudaetsya nebol'shoe ubyvanie v okrestnosti solnechnogo radiusa orbity i, kak minimum, otsutstvie ubyvaniya na periferii Galaktiki. Takoe slozhnoe povedenie krivoi vrasheniya opredelyaetsya slozhnym raspredeleniem mass v Galaktike, a takzhe tem faktom, chto Galaktika, kak my znaem iz predydushih paragrafov, sostoit iz podsistem s raznymi kinematicheskimi svoistvami. Ochevidno, chto na bol'shom rasstoyanii ot centra Galaktiki krivaya vrasheniya dolzhna imet' keplerovskii ubyvayushii harakter, odnako nablyudeniya pokazyvayut, chto tam, gde est' nablyudaemoe svetyasheesya veshestvo, krivaya vrasheniya vozmozhno dazhe ne dostigaet maksimuma.

Krivaya vrasheniya, sovmestno s drugimi dannymi, daet vozmozhnost' postroit' model' raspredeleniya mass v Galaktike. Etot vopros budet rassmotren v 15-i lekcii.

Publikacii s klyuchevymi slovami: zvezdnaya astronomiya Publikacii so slovami: zvezdnaya astronomiya
Sm. takzhe: Elene Vyacheslavovne Glushkovoi - 50 ! Konferenciya «Sovremennaya zvezdnaya astronomiya - 2014» Konferenciya "Sovremennaya zvezdnaya astronomiya" K 100-letiyu so dnya rozhdeniya Petra Grigor'evicha Kulikovskogo Lekcii po Galakticheskoi Astronomii. 5–8 Lekcii po Galakticheskoi Astronomii. 3–4 Lekcii po Galakticheskoi Astronomii. 1–2 Vse publikacii na tu zhe temu >>