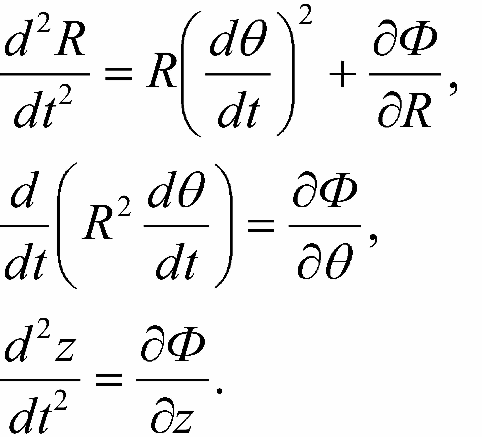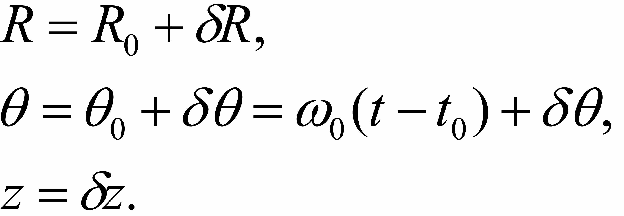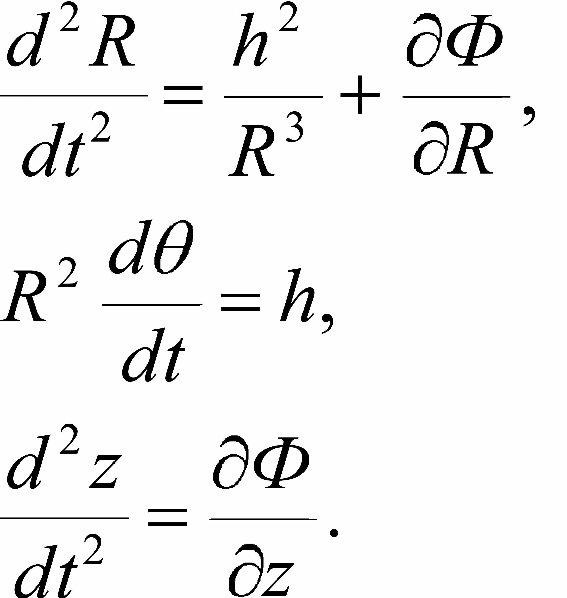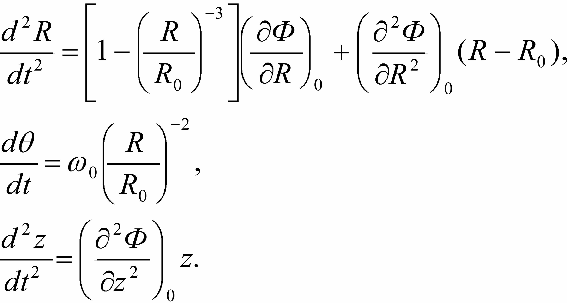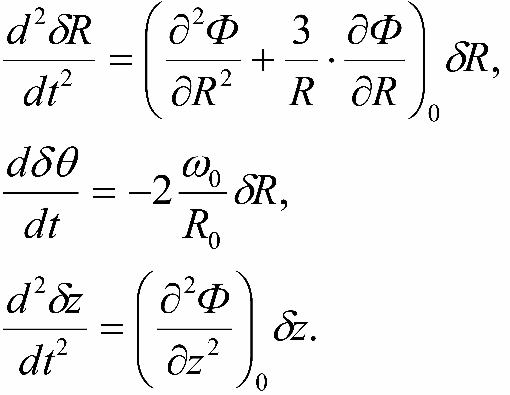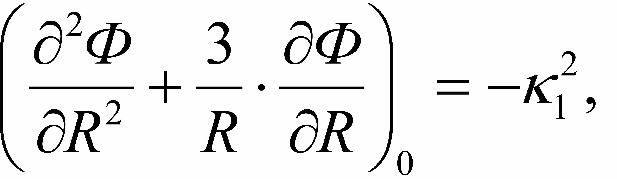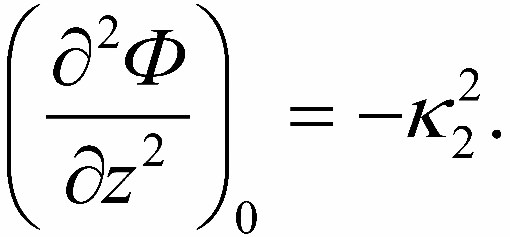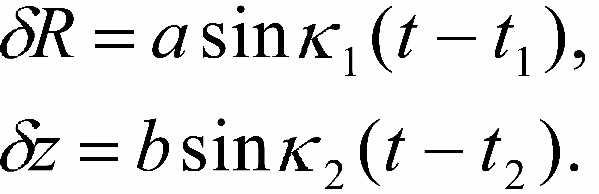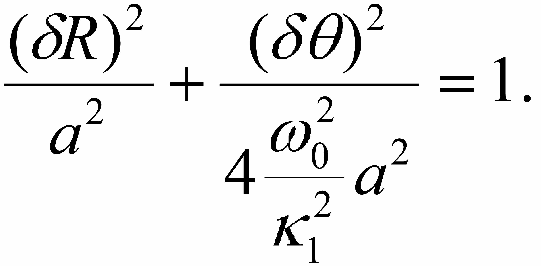16.1 Epiciklicheskoe priblizhenie
Izuchenie dvizhenii zvezd udobno provodit', ispol'zuya apparat issledovaniya galakticheskih orbit, tak kak orbity svyazyvayut nablyudaemye dvizheniya zvezd so svoistvami gravitacionnogo potenciala Galaktiki. Pri etom rezul'taty issledovanii vyrazhayutsya v bolee naglyadnoi forme, chem, naprimer, pri ispol'zovanii dispersii skorostei. Izuchenie galakticheskih orbit ispol'zuetsya pri issledovanii ustoichivosti zvezdnyh gruppirovok, naprimer dvizhushihsya eggenovskih grupp. Ponyatno, chto galakticheskie orbity vseh ob'ektov ogranicheny v prostranstve, inache Galaktika slilas' by s fonom. Tak kak dazhe galakticheskii disk imeet nenulevuyu tolshinu, orbity trehmerny i v obshem sluchae nezamknuty.
Ranee my uzhe sdelali vyvod, chto orbity zvezdy diska dolzhny byt' blizki k krugovym, poskol'ku ih ostatochnye skorosti sushestvenno men'she skorosti vrasheniya Galaktiki. V etom sluchae my mozhem linearizovat' uravneniya dvizheniya i poluchit' integriruemuyu sistemu differencial'nyh uravnenii. Uravneniya dvizheniya zvezdy v cilindricheskoi sisteme koordinat, podhodyashei dlya nashei osesimmetrichnoi Galaktiki, imeyut vid:
V etih vyrazheniyah
F = F(R,Θ, z) est' gravitacionnyi potencial Galaktiki. Zadav znacheniya prostranstvennyh koordinat i komponenty skorosti zvezdy v nekotoryi nachal'nyi moment vremeni, mozhno vychislit' polozhenie ob'ekta v lyuboi posleduyushii moment, reshiv sistemu (16-1).
Pust' gravitacionnyi potencial Galaktiki imeet cilindricheskuyu simmetriyu: F = F(R,z) . Togda vtoroe uravnenie (16-1) integriruetsya i daet tak nazyvaemyi integral ploshadei:
Uravneniya (16-1) - (16-2) reshayutsya analiticheski tol'ko v otdel'nyh, malo interesnyh chastnyh sluchayah, naprimer, dlya keplerovskih orbit, kogda vsya massa, sozdayushaya pole tyagoteniya, sosredotochena v tochke. Odnako dazhe dlya takih prostyh form potenciala, kak potencial Parenago, analiticheskih reshenii ne sushestvuet. Poetomu dlya issledovaniya svoistv galakticheskih orbit prihoditsya iskat' uproshayushie predpolozheniya.
Dvizhenie po orbite, blizkoi k krugovoi, mozhno predstavit' kak summu dvuh dvizhenii: dvizheniya po krugovoi orbite i nebol'shie otkloneniya ot etogo dvizheniya. Zapishem prostranstvennye koordinaty zvezdy v vide koordinat tochki, dvizhusheisya po krugovoi orbite i malyh popravok:
Zdes' R
0 = const - radius nekotoroi krugovoi orbity, sootvetstvuyushei zadannoi kineticheskoi energii zvezdy, i celikom lezhashei v ploskosti Galaktiki, a Θ
0 - azimutal'nyi galaktocentricheskii ugol, sootvetstvuyushii dvizheniyu po etoi orbite. Nazovem, dlya kratkosti, rassmatrivaemuyu orbitu var'irovannoi. Opredelim R
0 tak, chtoby postoyannaya ploshadei h dlya sootvetstvuyushei krugovoi orbity ravnyalas' znacheniyu etoi postoyannoi dlya rassmatrivaemoi var'irovannoi orbity. Perepishem uravneniya (16-1) s pomosh'yu integrala ploshadei v vide:
Opredelim chastotu vrasheniya Galaktiki na rasstoyanii R
0 ot osi ee vrasheniya iz integrala ploshadei kak
ω0 = h / R02. V etom sluchae iz pervogo uravneniya sistemy (16-1) mozhno poluchit':
gde nulevoi indeks oznachaet vzyatie proizvodnoi v tochke R
0. Razlagaya s ispol'zovaniem etogo vyrazheniya potencial
F = F(R,z) v ryad po stepenyam malyh velichin
(R - R0) i z i ostavlyaya v vyrazheniyah pervye stepeni koordinat, poluchaem:
Teper' podstavim v etu sistemu vyrazheniya (16-4), prenebregaya vtorymi i bolee vysokimi stepenyami variacii peremennyh. Poluchim sistemu:
Legko uvidet', chto vyrazheniya v skobkah pervogo i tret'ego uravnenii otricatel'ny. Poetomu mozhno vvesti oboznacheniya:
Teper' horosho vidno, chto pervoe i tret'e uravneniya predstavlyayut soboi uravneniya malyh kolebanii i legko integriruyutsya. Poluchaem:
Zdes' a, b, t
1, t
2 - postoyannye integrirovaniya. Podstavlyaya pervoe iz vyrazhenii (16-11) vo vtoroe uravnenie (16-8) poluchaem:
Takim obrazom, v ploskosti Galaktiki tochka, dvizhushayasya po pochti krugovoi orbite, opisyvaet ellips otnositel'no tochki, dvizhusheisya po sootvetstvuyushei krugovoi orbite. Po koordinate z tochka pri etom sovershaet garmonicheskie kolebaniya. Tak kak chastoty kolebanii v ploskosti Galaktiki i z-napravlenii ne sovpadayut, orbita poluchaetsya ne zamknutoi, ne lezhit v ploskosti i pri dvizhenii ob'ekta ona zapolnyaet simmetrichnuyu otnositel'no ploskosti Galaktiki trehmernuyu toroobraznuyu figuru vrasheniya.
Isklyuchaya vremya iz pervogo vyrazheniya (16-10) i vyrazheniya (16-11), poluchaem uravnenie ellipsa:
Dvizhenie po ellipsu v rassmotrennom priblizhenii napominaet dvizhenie po epiciklu, poetomu eto priblizhenie nazyvaetsya
epiciklicheskim priblizheniem, a velichinu nazyvayut epiciklicheskoi chastotoi. Velichinu pri etom mozhno nazvat' epiciklicheskoi amplitudoi. Legko pokazat', ispol'zuya vyrazhenie (16-9), chto epiciklicheskaya chastota mozhet byt' ocenena cherez postoyannye Oorta:
Dlya prinyatyh nami v kachestve standartnyh znachenii A = 15 km/s/kpk i V = -10 km/s/kpk, poluchaem dlya epiciklicheskoi chastoty velichinu 31.6 km/s/kpk. Eto oznachaet, chto period epiciklicheskih kolebanii sostavlyaet okolo 80% ot perioda vrasheniya Galaktiki na solnechnom galaktocentricheskom rasstoyanii.
Velichinu k22 - kvadrat chastoty kolebanii v napravlenii osi z, nazyvayut dinamicheskim parametrom, i oboznachayut C2. V zvezdnoi dinamike vyvoditsya vyrazhenie, svyazyvayushee etu chastotu s dispersiei skorostei v z-napravlenii i gradientom plotnosti veshestva v ploskosti Galaktiki:
gde
ρ - plotnost' veshestva - funkciya, zavisyashaya ot koordinat. Velichiny v pravoi chasti vyrazheniya (16-14) mozhno naiti iz nablyudenii i okazyvaetsya, chto v okrestnostyah Solnca
period kolebanii v z-napravlenii sostavlyaet okolo 45% ot perioda vrasheniya diska Galaktiki. Dlya polucheniya velichiny logarifmicheskogo gradienta plotnosti, vhodyashei v vyrazhenie (16-14), dostatochno vzyat' zvezdy odnogo tipa, naprimer krasnye giganty, i provesti zvezdnye podschety.
Rassmotrim, nakonec, kak poluchayutsya dinamicheskie ocenki plotnosti veshestva Galaktiki v okrestnostyah Solnca. Zapishem uravnenie Puassona v cilindricheskoi sisteme koordinat:
Mozhno pokazat', chto pervye dva slagaemyh vyrazhayutsya cherez postoyannye Oorta:
Tret'e slagaemoe v levoi chasti (16-16) est' opredelennyi nami vyshe dinamicheskii parametr. V rezul'tate dlya opredeleniya plotnosti veshestva v okrestnostyah Solnca poluchaem:
Imenno eto vyrazhenie ispol'zovalos' dlya polucheniya privedennogo ranee (sm.
12.1) znacheniya plotnosti veshestva v okrestnostyah Solnca. V privychnyh edinicah prinyatye nami znacheniya postoyannyh Oorta i velichina C = 70 km/s/kpk privodit k znacheniyu
ρ ≈ 6 • 10-24 g/sm3 .