Opredelenie rasstoyanii do zvezdnyh ob'ektov
3.1 Geometricheskie metody opredeleniya rasstoyanii do nebesnyh tel
Rassmotrim sposoby ocenki rasstoyanii do ob'ektov, ne svyazannye s analizom elektromagnitnogo izlucheniya etih ob'ektov. Raznoobrazie chisto geometricheskih metodov opredeleniya rasstoyanii yavlyaetsya sledstviem raznoobraziya izuchaemyh kosmicheskih ob'ektov. Zdes' my ne budem rassmatrivat' opredelenie rasstoyanii do otnositel'no blizkih ob'ektov, takih kak ISZ ili planety, gde ispol'zuyutsya metody radio i opticheskoi lokacii, i ostanovimsya na opredelenii rasstoyanii do zvezd, kotoroe yavlyaetsya osnovoi dlya opredeleniya galakticheskih i vnegalakticheskih rasstoyanii.
Pervym iz takih metodov rassmotrim metod trigonometricheskih parallaksov. Rasstoyaniya do zvezd neizmerimo bol'she ih diametrov, poetomu zvezdy obychno rassmatrivayutsya kak tochechnye ob'ekty. Pri etom na protyazhenii desyatkov i soten let ih dvizhenie otnositel'no Solnca s bol'shoi stepen'yu tochnosti mozhno rassmatrivat' kak ravnomernoe i pryamolineinoe. Esli perenesti sistemu koordinat v centr Zemli, to v nablyudaemoe dvizhenie zvezdy voidut dvizhenie Zemli otnositel'no Solnca i sobstvennoe dvizhenie zvezdy. V pervom priblizhenii dvizhenie Zemli vokrug Solnca rassmatrivaetsya kak dvizhenie po krugu radiusom 1 a.e. s periodom T = 1 god. Takim obrazom, my nablyudaem dva dvizheniya - ravnomernoe pryamolineinoe dvizhenie za schet sobstvennogo dvizheniya i dvizhenie po krugu v ploskosti, parallel'noi ploskosti ekliptiki.
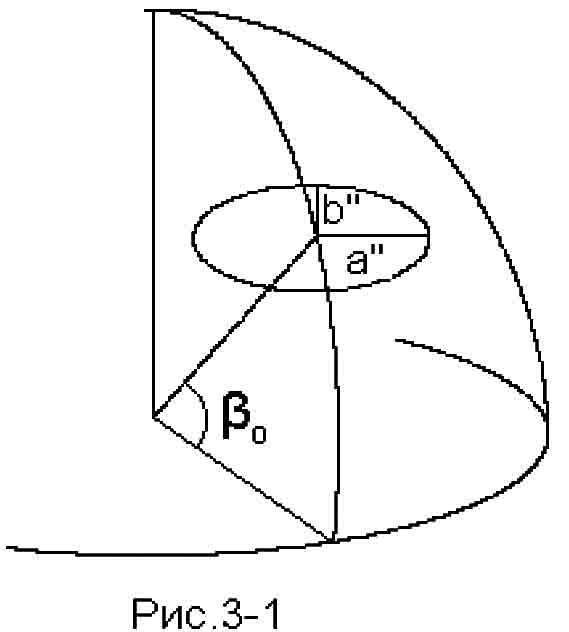
Proeciruya dvizhenie zvezdy na ploskost', kasatel'nuyu k nebesnoi sfere v tochke, yavlyayusheisya proekciei polozheniya zvezdy (sm. ris. 3-1), poluchim dvizhenie po ellipsu, bol'shaya os' kotorogo ravna a″, a malaya - b″ = a″ sin β0(zdes' β0 - eklipticheskaya shirota zvezdy), i pryamolineinoe dvizhenie centra ellipsa. Vsledstvie etogo v eklipticheskoi sisteme koordinat rassmatrivaemoe dvizhenie predstavlyaetsya vyrazheniyami:
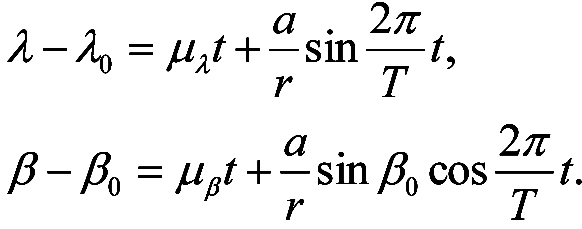
|
Zdes' r - rasstoyanie do zvezdy, 2π/T - uglovaya skorost' dvizheniya Zemli po orbite vokrug Solnca, μ - sootvetstvuyushaya komponenta sobstvennogo dvizheniya, vyrazhennogo v radianah, λ0 i β0 - eklipticheskie koordinaty centra ellipsa.
Vyrazhenie a/r est' sinus ugla, pod kotorym so zvezdy viden radius zemnoi orbity. Etot ugol, vyrazhennyi v sekundah dugi, nazyvaetsya godichnym parallaksom zvezdy, t.e. π = a/r. Chasto seichas vmesto termina
Vyrazheniya (3-1) mozhno ispol'zovat' dlya opredeleniya trigonometricheskih parallaksov zvezd. Na praktike opredelyayut bol'shoe chislo polozhenii zvezd v techenie dostatochno bol'shogo promezhutka vremeni (poryadka goda i bol'she), naprimer fotograficheskim metodom, i ispol'zuyut pervoe iz vyrazhenii (3-1), chashe vsego perepisannoe dlya ekvatorial'nyh koordinat, poluchaya znachenie trigonometricheskogo parallaksa metodom naimen'shih kvadratov. Pri etom obychno ispol'zuyutsya otnositel'nye opredeleniya, kogda opredelyayutsya smesheniya koordinat izmeryaemyh zvezd otnositel'no gruppy slabyh zvezd, dlya kotoryh trigonometricheskie parallaksy mozhno schitat' blizkimi k nulyu. V tablice 3-1 privedeny nazemnye opredeleniya trigonometricheskih parallaksov neskol'kih yarkih zvezd. Iz tablicy vidno, chto dazhe samye blizkie k Solncu zvezdy imeyut trigonometricheskie parallaksy menee odnoi uglovoi sekundy. Obratim vnimanie, chto sredi samyh vizual'no yarkih zvezd nekotorye okazyvayutsya ves'ma dalekimi ot nas.
Tablica 3-1
| Zvezda | π″ | Zvezda | π″ | |||
| α CMa (Sirius) | 0.375 | α CMi (Procion) | 0.288 | |||
| α Boo (Arktur) | 0.090 | α Ori (Betel'geize) | 0.005 | |||
| α Lyr (Vega) | 0.123 | α Proxima Cen | 0.762 | |||
| α Aur (Kapella) | 0.073 | α Cen A | 0.754 | |||
| β Ori (Rigel') | 0.001 | α Zvezda Barnarda | 0.552 | |||
Sleduyushim vazhneishim geometricheskim metodom opredeleniya rasstoyanii yavlyaetsya metod dvizhushegosya skopleniya. Sredi blizkih k Solncu rasseyannyh skoplenii i zvezdnyh grupp imeetsya neskol'ko tak nazyvaemyh dvizhushihsya, t.e. imeyushih zametnoe obshee dlya zvezd gruppirovki sobstvennoe dvizhenie, chto govorit o ne ochen' bol'shom rasstoyanii gruppirovki ot Solnca. Napravleniya sobstvennyh dvizhenii zvezd, prinadlezhashih takim gruppam, peresekayutsya v tochke radianta. Etot effekt yavlyaetsya sledstviem izvestnogo iz teorii perspektivy shozhdeniya parallel'nyh linii, kotoryi ochen' chetko pokazyvayut meteory, prinadlezhashie odnomu potoku.
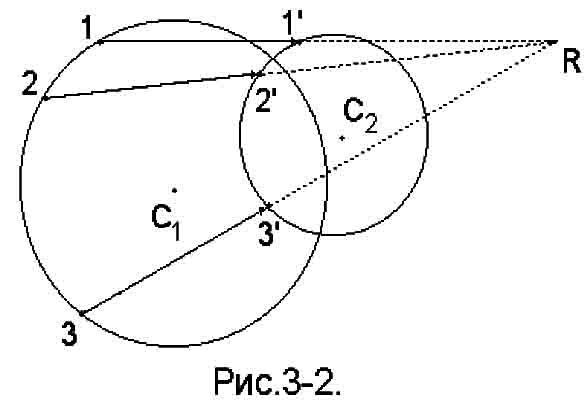 V nashem sluchae radiant est' tochka peresecheniya bol'shih krugov, provedennyh cherez zvezdy v napravlenii ih sobstvennyh dvizhenii. Etot effekt poyasnyaetsya risunkom 3-2. Na risunke bol'shoi okruzhnost'yu shematicheski pokazano zvezdnoe skoplenie v proekcii na nebesnuyu sferu v nekotoryi moment v proshlom, a men'shei okruzhnost'yu - to zhe skoplenie, udalivsheesya ot nas za nekotoroe vremya, chto privelo k umen'sheniyu ego uglovyh razmerov i smesheniyu ego centra za schet sobstvennogo dvizheniya skopleniya v celom. Yasno, chto my vybrali primer, kogda luchevaya skorost' skopleniya polozhitel'na. Tochkami 1, 2, 3 izobrazheny tri zvezdy i smeshenie etih zvezd v tochki 1', 2', 3' za schet sobstvennogo dvizheniya. Bukvoi R oboznacheno polozhenie radianta.
V nashem sluchae radiant est' tochka peresecheniya bol'shih krugov, provedennyh cherez zvezdy v napravlenii ih sobstvennyh dvizhenii. Etot effekt poyasnyaetsya risunkom 3-2. Na risunke bol'shoi okruzhnost'yu shematicheski pokazano zvezdnoe skoplenie v proekcii na nebesnuyu sferu v nekotoryi moment v proshlom, a men'shei okruzhnost'yu - to zhe skoplenie, udalivsheesya ot nas za nekotoroe vremya, chto privelo k umen'sheniyu ego uglovyh razmerov i smesheniyu ego centra za schet sobstvennogo dvizheniya skopleniya v celom. Yasno, chto my vybrali primer, kogda luchevaya skorost' skopleniya polozhitel'na. Tochkami 1, 2, 3 izobrazheny tri zvezdy i smeshenie etih zvezd v tochki 1', 2', 3' za schet sobstvennogo dvizheniya. Bukvoi R oboznacheno polozhenie radianta.
Esli izvestny koordinaty radianta i luchevye skorosti hotya by dlya neskol'kih zvezd skopleniya, mozhno nadezhno opredelit' individual'nye parallaksy zvezd - chlenov dvizhushegosya skopleniya. Znaya pryamoe voshozhdenie A i sklonenie D radianta, legko opredelit' uglovoe rasstoyanie kazhdoi zvezdy - chlena skopleniya ot radianta (na ris.3-2 eto otrezki 1'- R, 2'- R, 3' - R) po formule:
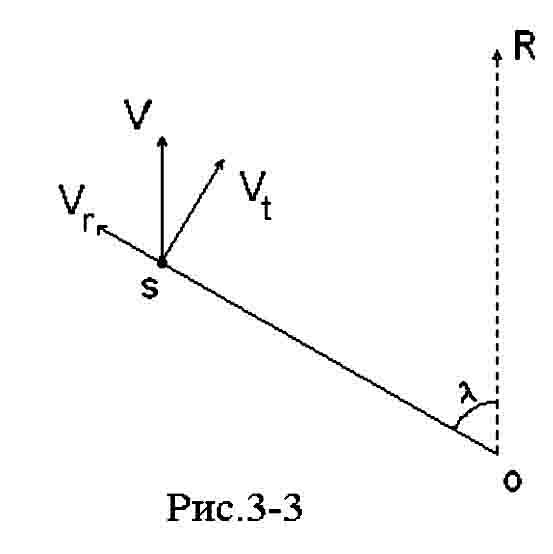 Iz ris.3-3, na kotorom v tochke O nahoditsya nablyudatel', R oboznachaet napravlenie na radiant, a v tochke S nahoditsya nablyudaemaya zvezda, vidno, chto Vr = V cos λ, gde V est' prostranstvennaya skorost' skopleniya. Izmeriv luchevuyu skorost' dlya neskol'kih zvezd skopleniya, mozhno poluchit' ocenku srednei prostranstvennoi skorosti skopleniya . Tangencial'naya skorost' zvezdy est':
Iz ris.3-3, na kotorom v tochke O nahoditsya nablyudatel', R oboznachaet napravlenie na radiant, a v tochke S nahoditsya nablyudaemaya zvezda, vidno, chto Vr = V cos λ, gde V est' prostranstvennaya skorost' skopleniya. Izmeriv luchevuyu skorost' dlya neskol'kih zvezd skopleniya, mozhno poluchit' ocenku srednei prostranstvennoi skorosti skopleniya . Tangencial'naya skorost' zvezdy est':
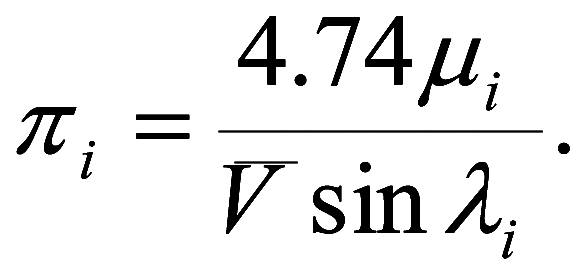
|
| r = d ctga |
M¤
|
Publikacii s klyuchevymi slovami:
zvezdnaya astronomiya
Publikacii so slovami: zvezdnaya astronomiya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |