3.2 Srednie (vekovye) parallaksy
V opisyvaemom metode dlya opredeleniya srednih parallaksov zvezd ispol'zuetsya dvizhenie Solnca otnositel'no etih zvezd. Izmeryaya vidimye smesheniya zvezd, vyzvannye etim dvizheniem, mozhno opredelit' rasstoyanie do poslednih, tak kak uglovye smesheniya zvezd proporcional'ny ih rasstoyaniyam ot Solnca.
Nedostatkom metoda yavlyaetsya to, chto krome dvizheniya, yavlyayushegosya otrazheniem dvizheniya Solnca, zvezdy imeyut svoi, tak nazyvaemye "pekulyarnye" (ostatochnye) dvizheniya, kotorye neobhodimo otdelyat' ot parallakticheskogo dvizheniya. Pri etom prihoditsya vvodit' predpolozhenie, chto pekulyarnye dvizheniya yavlyayutsya haoticheskimi, chto, kak my uvidim v posleduyushih lekciyah, ne vsegda vypolnyaetsya.
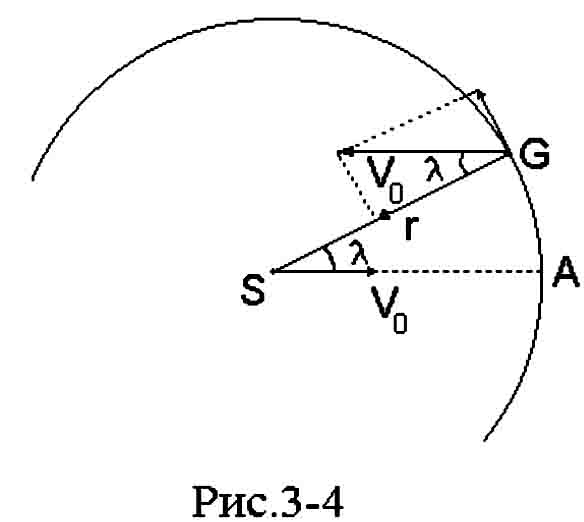Pust' zvezda G nahoditsya na rasstoyanii r = π-1 ot Solnca (sm. ris.3-4), dvigayushegosya so skorost'yu V0 v napravlenii svoego apeksa A. Pust' V oboznachaet prostranstvennuyu skorost' zvezdy otnositel'no Solnca. My mozhem zapisat':
gde V
S est' skorost' pekulyarnogo dvizheniya zvezdy otnositel'no toi gruppy zvezd, po otnosheniyu k kotoroi opredelena skorost' Solnca. Razlozhim kazhdyi iz treh vektorov vyrazheniya (3-6) na tri sostavlyayushie, pervaya iz kotoryh napravlena po pryamoi zvezda - Solnce, vtoraya - po kasatel'noi k okruzhnosti, prohodyashei cherez zvezdu s centrom v Solnce, ploskost' kotoroi prohodit cherez vektor V
0, a tret'ya sostavlyayushaya - perpendikulyarno dvum drugim (na ris.3-4 ne pokazana). Vyrazim komponenty vektorov cherez parallaks zvezdy, luchevuyu skorost' Vr i komponenty sobstvennogo dvizheniya otnositel'no tochki apeksa, kotorye oboznachim kak
v, τ, vS, τS. Pri etom komponenty vektorov, vhodyashih v vyrazhenie (3-6) budut ravny:
Dlya vtoryh komponentov vektorov vyrazhenie (3-6) s uchetom (3-7) dast:
Usrednim eto vyrazhenie po vsem vybrannym zvezdam. V etom sluchae, soglasno sdelannomu vyshe predpolozheniyu o haotichnosti pekulyarnyh sostavlyayushih skorostei zvezd, srednee znachenie
vS = 0. Minimizaciya raznostei levoi i pravoi chastei (3-8) privodit k vyrazheniyu dlya srednego parallaksa gruppy zvezd:
Mozhno takzhe, esli izvestny luchevye skorosti zvezd, ispol'zovat' tret'i komponenty vektorov iz vyrazhenii (3-7). Vnov' ispol'zuem dopushenie o haotichnosti raspredeleniya pekulyarnyh skorostei, chto daet vozmozhnost', vzyav vmesto velichin
vs velichiny 4.74
τs/π i, ispol'zuya ochevidnoe vyrazhenie
Vr = VrS + V0cosλ, zapisat':
gde v znamenatele stoit srednee iz luchevyh skorostei, iz kotoryh vychteny velichiny
V0cosλ. Yasno, chto dlya opredeleniya srednih absolyutnyh zvezdnyh velichin po privedennym formulam sleduet vybirat' odnorodnye po svoistvam zvezdy (naprimer - peremennye opredelennogo tipa) i delit' ih na podgruppy po vidimoi zvezdnoi velichine, chto v etom sluchae sootvetstvuet razdeleniyu na podgruppy po rasstoyaniyam.
Ukazannyi metod horosho posluzhil astronomam v HH veke, i ne ustarel v nastoyashee vremya. Delo v tom, chto opredelenie absolyutnyh zvezdnyh velichin odnim metodom ne daet polnoi uverennosti, chto my ne zametili kakoi-libo sistematicheskoi oshibki v nablyudatel'nyh dannyh ili metodike ih ispol'zovaniya, tak chto sravnenie rezul'tatov, poluchennyh raznymi metodami, povyshaet nadezhnost' ocenok. Vmeste s tem sleduet otmetit', chto primenenie kinematicheskih metodov opredeleniya rasstoyanii do zvezd trebuet vysokoi odnorodnosti kinematicheskih svoistv ispol'zuemyh zvezd, chto dazhe v okrestnostyah Solnca vypolnyaetsya ploho.
