9.3 Raspredelenie Shvarcshil'da

Lekciya 9. Dvizhenie Solnca v prostranstve i ostatochnye skorosti zvezd

9.3 Raspredelenie Shvarcshil'da

Kak izvestno iz statisticheskoi mehaniki, polnoe opisanie sistemy vzaimodeistvuyushih chastic mozhno dat', esli znat' raspredelenie chastic po koordinatam i skorostyam - tak nazyvaemuyu funkciyu fazovoi plotnosti. Esli prointegrirovat' takuyu funkciyu po skorostyam, to poluchim prostranstvennoe raspredelenie chastic. Prostranstvennoe raspredelenie zvezd i gazovyh oblakov v Galaktike my rassmotreli v predydushih lekciyah. Esli prointegrirovat' funkciyu fazovoi plotnosti po koordinatam, my poluchim raspredelenie skorostei chastic, a isklyuchiv potokovye dvizheniya - naprimer vrashenie Galaktiki i dvizhenie Solnca v prostranstve, my poluchim raspredelenie ostatochnyh skorostei, kotoroe mozhno issledovat' na osnove nablyudatel'nyh dannyh. Nekotorye svedeniya o dispersii skorostei my uzhe poluchili v predydushih paragrafah. Rassmotrim raspredelenie ostatochnyh skorostei zvezd v Galaktike bolee podrobno.

Chtoby issledovat' raspredelenie ostatochnyh skorostei zvezd vvedem funkciyu raspredeleniya vektorov skorostei V takom sluchae gde dN est' chislo zvezd, vektory ostatochnyh skorostei kotoryh zaklyucheny mezhdu i Esli by raspredelenie vektorov skorostei bylo sluchainym i dlya kazhdoi zvezdy yavlyalos' sledstviem mnogih vzaimodeistvii, izmenyayushih skorost', to vyrazhalas' by trehmernym normal'nym raspredeleniem:

gde A est' tak nazyvaemaya kovariacionnaya matrica, soderzhashaya dispersii i kovariacii velichin u, v i w, a vo vnutrennih skobkah pod znakom eksponenty stoit polnaya kvadratichnaya forma ot komponentov skorosti zvezdy:

Lineinye chleny zdes' ne privedeny, tak kak po opredeleniyu ostatochnoi skorosti oni ravny nulyu. Otmetim takzhe, chto v obshem sluchae, esli rassmatrivat' raspredelenie skorostei v Galaktike v celom, koefficienty, vhodyashie v vyrazhenie (9-6), est' funkcii koordinat. Esli rassmatrivat' tol'ko blizhaishie okrestnosti Solnca, to koefficienty mozhno schitat' konstantami.

Esli priravnyat' pokazatel' stepeni v vyrazhenii (9 -5) konstante, to poluchim urovnevuyu poverhnost', opisyvayushuyu formu raspredeleniya. V chastnosti, takie poverhnosti dlya trehmernogo normal'nogo raspredeleniya yavlyayutsya trehosnymi ellipsoidami. Vpervye opisanie raspredeleniya ostatochnyh skorostei zvezd s pomosh'yu takoi plotnosti raspredeleniya predlozhil v nachale HH-go veka Shvarcshil'd. V bolee prostom sluchae, kogda napravleniya osei ellipsoida skorostei sovpadayut s osyami koordinat, kovariacii (mnozhiteli pri proizvedeniyah raznyh komponentov) ravny nulyu i parametrami raspredeleniya okazyvayutsya tol'ko dispersii skorostei po trem koordinatam - dispersii komponentov vektora ostatochnoi prostranstvennoi skorosti. Raspredelenie Shvarcshil'da pri etom prinimaet sleduyushii vid: gde σ_u, σ_v, σ_w oboznachayut sootvetstvuyushie dispersii ostatochnyh skorostei. Kak izvestno, kvadratichnuyu formu mozhno privesti k normal'nomu vidu metodami lineinoi algebry, tak chto iz nablyudatel'nyh dannyh my mozhem poluchit' ne tol'ko dispersii skorostei, no i ostal'nye konstanty vyrazheniya (9-5), znachit mozhno ocenit' ne tol'ko velichiny dispersii skorostei, no i orientaciyu ellipsoida skorostei v prostranstve.

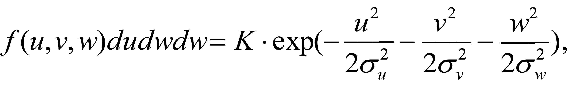
V techenie HH-go veka mnogo usiliya bylo zatracheno na opredelenie parametrov ellipsoidov skorostei, tak kak eti parametry tesno svyazany s dinamikoi Galaktiki. Izuchalis' kak dispersii skorostei, tak i orientaciya ellipsoida skorostei v prostranstve. Kstati, napravlenie bol'shoi osi ellipsoida skorostei nazyvaetsya napravleniem verteksa, eto nazvanie prishlo iz tak nazyvaemoi teorii dvuh potokov - odnoi iz popytok opisaniya ostatochnyh skorostei, imeyushei v nastoyashee vremya lish' istoricheskii interes. Poluchit' parametry ellipsoida skorostei iz nablyudatel'nyh dannyh dostatochno legko. Dlya etogo mozhno ispol'zovat' ili luchevye skorosti, ili sobstvennye dvizheniya i rasstoyaniya do issleduemyh ob'ektov. Osobenno legko poluchit' ih iz komponentov polnoi prostranstvennoi skorosti. Dlya etogo nado k vyrazheniyu (9-5) dobavit' eshe odno neizvestnoe - konstantu, a dlya vyborki nablyudaemyh prostranstvennyh ostatochnyh skorostei ispol'zovat' (9-6) kak uslovnye uravneniya, nahodya parametry metodom naimen'shih kvadratov. Etot metod vpervye byl predlozhen v nachale HH veka Dzevul'skim. Ispol'zovanie otdel'no luchevyh skorostei ili sobstvennyh dvizhenii bolee trudoemko, pri etom rezul'taty sil'no zavisyat ot raspredeleniya ispol'zuemyh zvezd po nebu - ono dolzhno byt' po vozmozhnosti ravnomernym, chego dobit'sya dostatochno trudno.

Eshe legche poluchit' po prostranstvennym skorostyam parametry vyrazheniya (9-7). Dlya etogo nado prosto vychislit' sootvetstvuyushie dispersii komponentov ostatochnoi skorosti: V § 15.3 my rassmotrim svyaz' dispersii skorostei s dinamicheskimi svoistvami Galaktiki na primere modeli stacionarnoi Galaktiki. Stacionarnost' pri etom oznachaet neizmennost' funkcii fazovoi plotnosti so vremenem. Otmetim tol'ko, chto eta model' privodit k sovershenno opredelennym sootnosheniyam mezhdu dispersiyami komponentov ostatochnyh skorostei. A imenno, v etom sluchae dve bol'shie i ravnye po velichine poluosi dolzhny byt' napravleny na centr Galaktiki i perpendikulyarno ploskosti diska (v napravlenii osi z). Malaya poluos' dolzhna byt' napravlena v storonu galakticheskogo vrasheniya. A otnoshenie maloi poluosi k bol'shoi pri etom opredelyaetsya tol'ko krivoi krugovyh skorostei vrasheniya Galaktiki i dlya maloi okrestnosti Solnca dolzhno vypolnyat'sya sootnoshenie: gde A i V est' tak nazyvaemye postoyannye Oorta, takzhe opredelyaemye iz nablyudenii. Otmetim, chto etot rezul'tat poluchaetsya dazhe pri bolee obshih predpolozheniyah o forme raspredeleniya ostatochnyh skorostei, chem zadavaemoe ellipsoidom Shvarcshil'da (9-7), tak kak zdes' dostatochno, chtoby plotnost' raspredeleniya skorostei imela vid f = f(Q) gde Q est' polnaya kvadratichnaya forma ot komponent ostatochnoi skorosti, a funkciya f ne obyazatel'no yavlyalas' eksponencial'noi. Takzhe otmetim, chto pri standartnyh znacheniyah postoyannyh Oorta (A = 15 km/s/kpk i V = -10 km/s/kpk) my poluchaem otnoshenie dispersii Etu velichinu mozhno sravnit' s rezul'tatami obrabotki nablyudatel'nyh dannyh.

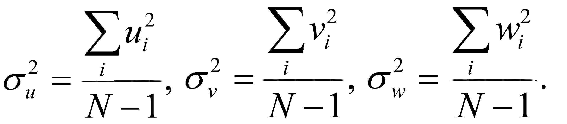
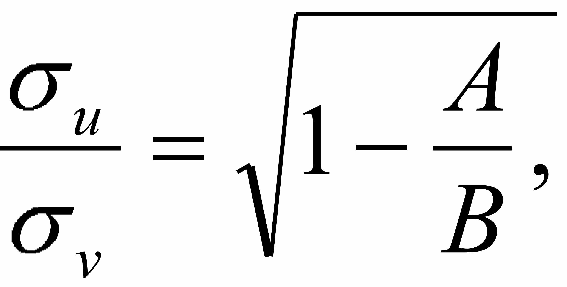
Publikacii s klyuchevymi slovami: zvezdnaya astronomiya Publikacii so slovami: zvezdnaya astronomiya
Sm. takzhe: Elene Vyacheslavovne Glushkovoi - 50 ! Konferenciya «Sovremennaya zvezdnaya astronomiya - 2014» Konferenciya "Sovremennaya zvezdnaya astronomiya" K 100-letiyu so dnya rozhdeniya Petra Grigor'evicha Kulikovskogo Lekcii po Galakticheskoi Astronomii. 5–8 Lekcii po Galakticheskoi Astronomii. 3–4 Lekcii po Galakticheskoi Astronomii. 1–2 Vse publikacii na tu zhe temu >>