Astronet > Zvezdnye skopleniya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Zvezdnye skopleniya << 3.2 Trigonometricheskie, dinamicheskie i spektral'nye parallaksy | Oglavlenie | 3.4 Diagrammy Hercshprunga-Ressela. Opredelenie rasstoyanii do skoplenii po velichinam i spektral'nym klassam zvezd >>

3.3 Gruppovye parallaksy

Gruppovymi parallaksami nazyvayutsya opredelyaemye s pomosh'yu formuly (1.1) individual'nye parallaksy zvezd, vhodyashih v sostav dvizhushihsya skoplenii (sm. § 1.6). Kak pokazyvaet eta formula, tochnost' gruppovyh parallaksov zavisit ot tochnosti opredeleniya luchevyh skorostei, sobstvennyh dvizhenii i koordinat tochki peresecheniya bol'shih krugov, opredelyaemyh etimi dvizheniyami na nebesnoi sfere. Pri etom v otnoshenii kazhdoi individual'noi zvezdy delaetsya neyavnoe (no, nesomnenno, sushestvennoe) dopushenie o bezuslovnoi prinadlezhnosti ee k dannomu dvizhushemusya zvezdnomu skopleniyu. V kazhdom konkretnom sluchae eto dopushenie mozhet okazat'sya nevernym.

Dlya opredeleniya koordinat apeksa (ili radianta) dvizhushegosya skopleniya mozhno ispol'zovat' mnogochislennye metody, predlozhennye v zvezdnoi astronomii dlya nahozhdeniya apeksa dvizheniya Solnca ili v meteornoi astronomii dlya nahozhdeniya radiantov meteornyh potokov. Podrobnoe izlozhenie etih metodov mozhno naiti v knige Polaka (1935).

Rassmotrim razrabotannyi Rasmusonom (1911; 1921) metod, osnovannyi na metodike Bolina (1905). V svyazi s tem, chto v nekotorye iz formul Rasmusona vkralis' oshibki, po udivitel'nomu stecheniyu obstoyatel'stv chastichno sohranivshiesya i v izlozhenii etogo metoda Polakom, poprobuem vosproizvesti eti formuly po vozmozhnosti bez oshibok.

Na ris. 12 izobrazhena nebesnaya sfera. R - polyus ekvatorial'noi sistemy koordinat; S - zvezda; α, δ - ee ekvatorial'nye koordinaty; μ - vektor sobstvennogo dvizheniya zvezdy, dvizhusheisya po bol'shomu krugu, polyus kotorogo - Q; A, D - ekvatorial'nye koordinaty etogo polyusa; K - apeks dvizhushegosya skopleniya, kotoromu prinadlezhit zvezda S; A₀, D₀ - koordinaty apeksa; K - uglovoe rasstoyanie zvezdy ot apeksa; q - ugol mezhdu napr avleniem sobstvennogo dvizheniya zvezdy i prohodyashim cherez nee krugom skloneniya.

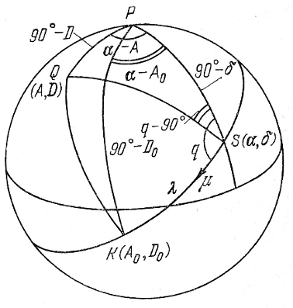
Ris. 12. Shema, poyasnyayushaya vyvod formul (3.5)-(3.8).

Pol'zuyas' sootnosheniyami μ_αcos δ = μ sin φ , μ_δ = μ cos φ , gde φ - pozicionnyi ugol izvestnogo sobstvennogo dvizheniya zvezdy, svyazannyi s uglom q sootnosheniem q = 360°; - φ (esli eto dvizhenie opredeleno absolyutno tochno), μ_α i μ_δ - komponenty etogo dvizheniya po α i δ, iz treugol'nika PQS nahodim:

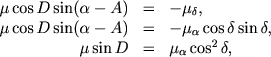
$\begin{array}{rl} \mu \cos D \sin (\alpha - A) \;\; = & -\mu_{\delta}, \\ \mu \cos D \sin (\alpha - A) \;\; = & -\mu_{\alpha} \cos \delta \sin\delta, \\ \mu \sin D \;\; = & \mu_{\alpha} \cos^2 \delta , \end{array}$ (3.5)

Po etim formulam dlya kazhdoi zvezdy vychislyayutsya koordinaty sootvetstvuyushego polyusa A, D.

Rassmatrivaya treugol'nik QPK, poluchim sootnoshenie

$-\tg D = x \cos A + y \sin A,$ (3.6)

gde

$\begin{array}{c} x = \cos A_0 \ctg D_0 , \\ y = \sin A_0 \ctg D_0 . \end{array}$ (3.7)

Reshaya po sposobu naimen'shih kvadratov sistemu uslovnyh uravnenii vida (3.6), nahodim velichiny h, u, posle chego po formulam (3.7) opredelyayutsya znacheniya A₀, D₀. Nakonec, rassmatrivaya treugol'nik KPS, netrudno vyvesti formuly, pozvolyayushie naiti dlya kazhdoi zvezdy znacheniya λ i q:

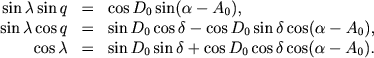
$\begin{array}{rl} \sin \lambda \sin q \;\; = & \cos D_0 \sin (\alpha - A_0), \\ \sin \lambda \cos q \;\; = & \sin D_0 \cos \delta - \cos D_0 \sin\delta \cos (\alpha - A_0), \\ \cos \lambda \;\; = & \sin D_0 \sin \delta + \cos D_0 \cos\delta \cos (\alpha - A_0) . \end{array}$ (3.8)

Znaya luchevuyu skorost' V_r hotya by odnoi zvezdy dvizhushegosya skopleniya, nahodim V (prostranstvennuyu skorost' skopleniya) iz sootnosheniya V_r = V cos λ, a zatem, po formule (1.1) , parallaks lyuboi zvezdy, schitayusheisya ego chlenom.

V metode Bolina - Rasmusona dlya nahozhdeniya apeksa ispol'zuyutsya tol'ko sobstvennye dvizheniya zvezd. V chasto primenyavshemsya dlya resheniya toi zhe zadachi metode Sharl'e (1914) ispol'zuyutsya takzhe i izvestnye luchevye skorosti zvezd skopleniya. Tak kak metod Sharl'e podrobno izlozhen v rabotah Rasmusona (1921) i Polaka (1935), my ogranichimsya privedeniem osnovnyh ego formul. Schitaya, chto prostranstvennye skorosti V vseh chlenov skopleniya odinakovy, mozhno napisat' sleduyushie vyrazheniya dlya ih komponentov ξ , η ,ζ v pryamougol'noi ekvatorial'noi sisteme koordinat (os' ξ napravlena v tochku vesennego ravnodenstviya, os' η lezhit v ekvatorial'noi ploskosti, os' ζ napravlena k severnomu polyusu mira):

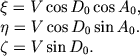
$\begin{array}{l} \xi = V\cos D_0 \cos A_0 , \\ \eta = V\cos D_0 \sin A_0 . \\ \zeta = V\sin D_0. \end{array}$ (3.9)

V to zhe vremya dlya kazhdoi zvezdy skopleniya vypolnyaetsya

$ax+by+c=0 ,$ (3.10)

gde

$\begin{array}{l} a = -\mu_{\alpha} \cos \delta \sin\delta \cos\alpha + \mu_{\delta} \sin \alpha, \\ b = -\mu_{\alpha} \cos \delta \sin\delta \sin\alpha - \mu_{\delta} \cos \alpha, \\ c = \mu_{\alpha} \cos \delta \sin\delta , \end{array}$ (3.11)

a

$x = \frac{\xi}{\zeta}, \quad y = \frac{\eta}{\zeta} ,$ (3.12)

prichem komponenty sobstvennogo dvizheniya v (3.11) vyrazheny v radianah. Vychisliv dlya kazhdoi zvezdy znacheniya a, b, c, nahodim putem resheniya po sposobu naimen'shih kvadratov sistemy uslovnyh uravnenii vida (3.10) znacheniya h i y, a zatem - koordinaty apeksa A₀, D₀ iz ochevidnyh sootnoshenii

$\tg A_0 = \frac{y}{x}, \quad \sin D_0 = \frac{1}{\sqrt{1+x^2 +y^2}}.$ (3.13)

Dal'neishie vychisleniya provodyatsya tak zhe, kak v metode Bolina - Rasmusona. V sushnosti, kak pokazal, naprimer, Smart (1938), osnovnye uravneniya metodov Bolina - Rasmusona i Sharl'e prakticheski identichny.

V 1945 g. Sirc (1945) obratil vnimanie na to, chto neposredstvennoe primenenie formul Sharl'e vedet k poyavleniyu sistematicheskoi oshibki v polozhenii apeksa, a sledovatel'no, i v opredelenii rasstoyaniya do dvizhushegosya skopleniya. Delo v tom, chto, kak vidno iz uravnenii (3.10) i (3.11), koefficienty normal'nyh uravnenii, sostavlyaemyh pri reshenii sistemy uslovnyh uravnenii (3.10), soderzhat opredelyaemye iz nablyudenii velichiny μ_α, μ_δ, iskazhennye oshibkami izmerenii. Sirc pokazal, chto pri etom proishodit sistematicheskoe preuvelichenie koefficientov normal'nyh uravnenii na velichiny, yavlyayushiesya funkciyami kvadratov oshibok izmereniya znachenii μ_α, μ_δ; sootvetstvenno iskazhaetsya i reshenie sistemy normal'nyh uravnenii. Dlya ucheta etoi oshibki, nazvannoi Sirsom oshibkoi regressii, neobhodimo predvaritel'no ispravit' koefficienty normal'nyh uravnenii. Oshibkoi regressii mozhno prenebrech' tol'ko v sluchae ochen' tochnyh izmerenii. Analogichnye trudnosti voznikayut i v metode Bolina - Rasmusona, v kotorom oshibki sobstvennyh dvizhenii v neyavnom vide vhodyat v koefficienty uslovnyh uravnenii vida (3.6), opredelyaemye s pomosh'yu ravenstv (3.5).

No etim ne ischerpyvayutsya nedostatki metodov Sharl'e i Bolina - Rasmusona. Pitri (1949) ukazal na neustoichivost' reshenii sistem uravnenii, ispol'zuemyh v etih metodah, osobenno zametnuyu v teh sluchayah, kogda skoplenie zanimaet ogranichennuyu oblast' na nebe, a tochka shozhdeniya sobstvennyh dvizhenii udalena ot nego na znachitel'noe rasstoyanie. Chtoby spravit'sya s etoi trudnost'yu, Pitri predlozhil metod nahozhdeniya differencial'nyh popravok k predvaritel'no naidennym s pomosh'yu odnogo iz opisannyh vyshe sposobov koordinatam apeksa, t.e. utochneniya polozheniya apeksa. Odnovremenno podobnyi metod byl nezavisimo predlozhen Roman (1949) i s teh por uspeshno ispol'zuetsya raznymi avtorami, kazhdyi iz kotoryh vidoizmenyaet ego v sootvetstvii so svoimi zadachami. My rassmotrim ego v traktovke Veimana i dr. (1965), naibolee blizkoi k pervonachal'nomu izlozheniyu Pitri, kotoryi, po-vidimomu, ne byl znakom s rabotoi Sirsa (1945) i ne podozreval, chto ego formuly v to zhe vremya pozvolyayut izbezhat' oshibki regressii.

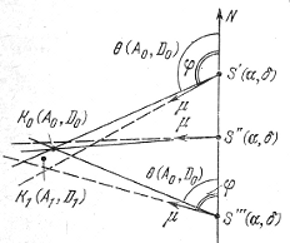
Ris. 13. Shema, poyasnyayushaya vyvod formul (3.14)-(3.19).

Pust' K₁ (A₁, D₁) na ris. 13 - predvaritel'noe polozhenie apeksa, K₀ (A₀, D₀) - istinnoe ego polozhenie, yavlyayusheesya tochkoi peresecheniya izobrazhennyh pryamymi liniyami bol'shih krugov, prohodyashih cherez kazhduyu iz zvezd skopleniya (S', S",...); vdol' etih krugov byli by napravleny sobstvennye dvizheniya rassmatrivaemyh, zvezd, esli by oshibki ih opredeleniya byli ravny nulyu, a sami zvezdy dvigalis' v prostranstve s ravnymi po velichine i parallel'nymi skorostyami.

Pust' θ(A₀, D₀) - pozicionnye ugly upomyanutyh bol'shih krugov pri tochkah s koordinatami α , β. Iz dvuh pervyh formul sistemy (3.8), uchityvaya, chto q = 2π - θ, nahodim dlya opredeleniya etih uglov sootnoshenie

$\ctg \theta (A_0, D_0) = \tg D_0 \cos\delta \cosec (A_0-\alpha) - \sin\delta \ctg (A_0-\alpha) .$ (3.14)

Analogichnoe sootnoshenie spravedlivo dlya pozicionnyh uglov θ(A₁, D₁) bol'shih krugov, prohodyashih cherez tochku K₁ i tochki s koordinatami α , β:

$\ctg \theta (A_1, D_1) = \tg D_1 \cos\delta \cosec (A_1-\alpha) - \sin\delta \ctg (A_1-\alpha) .$ (3.15)

Vychisliv po etomu sootnosheniyu dlya kazhdoi zvezdy znacheniya θ(A₁, D₁), nahodim dlya vseh zvezd znacheniya

$\Delta\theta = \phi - \theta (A_1, D_1),$ (3.16)

gde φ - pozicionnye ugly nablyudaemyh sobstvennyh dvizhenii etih zvezd.

Prinyav oboznacheniya ΔA = A₀ - A₁, ΔD = D₀ - D₁, mozhem zapisat' s tochnost'yu do chlenov pervogo poryadka:

$\theta (A_0, D_0) - \theta (A_1, D_1) = \frac{\partial\theta (A_1, D_1)}{\partial A_1} \Delta A + \frac{\partial\theta (A_1, D_1)}{\partial D_1} \Delta D .$ (3.17)

Tak kak tochka K₀ dolzhna byt' blizhaishei k napravleniyam sobstvennyh dvizhenii vseh zvezd skopleniya, my mozhem otozhdestvit' chlen θ(A₀, D₀) v sootnoshenii (3.17) s chlenom φ v sootnoshenii (3.16) i sostavit' ryad uslovnyh uravnenii

$\theta (A_0, D_0) - \theta (A_1, D_1) = \Delta\theta ,$ (3.18)

kotorye, uchityvaya (3.15) i (3.16), mozhno predstavit' v vide

$\begin{array}{l} [\ctg (A_1-\alpha) \cos \theta (A_1, D_1) \sin \theta (A_1, D_1) - \sin\delta\sin^2 \theta (A_1, D_1)]\Delta A - \\ - \sec^2 D_1 \cos\delta \cosec (A_1-\alpha)\sin^2 \theta (A_1, D_1) \Delta D = \Delta \theta . \end{array}$ (3.19)

Kazhdomu iz uslovnyh uravnenii sleduet pridat' ves v sootvetstvii s veroyatnoi oshibkoi ε_φ ugla φ , opredelyaemoi iz sootnosheniya

$\epsilon_{\phi}^2 = \frac{\epsilon_{\alpha}^2 \cos^2 \phi + \epsilon_{\delta}^2 \sin^2 \phi}{\mu^2} ,$ (3.20)

gde ε_α i ε_δ - veroyatnye oshibki μ_α i μ_δ.

Reshaya poluchennuyu sistemu uslovnyh uravnenii vida (3.19) po sposobu naimen'shih kvadratov, nahodim popravki ΔA i ΔD, kotorye nuzhno pridat' k ekvatorial'nym koordinatam A₁, D₁ predvaritel'nogo apeksa dlya togo, chtoby poluchit' uluchshennye koordinaty apeksa A₀, D₀. Oshibka regressii v dannom sluchae ne voznikaet, tak kak koefficienty uslovnyh uravnenii (3.19), a znachit, i sootvetstvuyushih im normal'nyh uravnenii yavlyayutsya tochnymi chislami.

Sushestvuyut i drugie metody opredeleniya tochnogo polozheniya tochki shozhdeniya sobstvennyh dvizhenii zvezd skopleniya, nazyvaemoi chasto verteksom. Kak odnu iz interesnyh modifikacii metoda differencial'nyh popravok mozhno upomyanut' metodiku Hensona (1975), na opisanii kotoroi my uzhe ne mozhem ostanavlivat'sya.

V metode Brauna (1950) ispol'zuetsya princip maksimal'nogo pravdopodobiya, sostoyashii v tom, chto ishutsya takie koordinaty verteksa, pri kotoryh zavisyashaya ot nih tak nazyvaemaya funkciya pravdopodobiya L dostigaet maksimuma, t.e. udovletvoryayutsya uravneniya

$\frac{\partial L}{\partial A_0} = 0, \quad \frac{\partial L}{\partial D_0} = 0 .$ (3.21)

Zdes' funkciya L imeet vid

$L = \prod\limits_{i=1}^n g_i (v_i) ,$ (3.4)

gde

$v_i = \ctg\phi_i = (\mu_\delta / \mu_\alpha)_i .$ (3.23)

(n - chislo zvezd, φ_i - pozicionnye ugly ih sobstvennyh dvizhenii), a g_i (v_i)dv_i - veroyatnost' nahozhdeniya znacheniya v_i v intervale ot v_i do v_i + dv_i. Esli srednie kvadratichnye oshibki opredeleniya μ_α i μ_δ oboznachit' cherez σ(μ_α), σ(μ_δ), prinyat', chto raspredeleniya μ_α i μ_δ otnositel'no ih istinnyh znachenii ξ i η yavlyayutsya gaussovymi, i vvesti oboznacheniya

$a=\frac{\eta}{\xi} = \ctg \theta (A_0, D_0), \quad b=\frac{\xi}{\sigma (\mu_\alpha)}, \quad c=\frac{\sigma (\mu_\delta)}{\sigma (\mu_\alpha)} ,$ (3.24)

to mozhno pokazat', chtoby

$g(v) = \frac{1}{\pi} \left[\left(\frac{c}{v^2 + c^2}\right) e^{-\frac{1}{2} b^2 (1+\frac{a^2}{c^2})} + \frac{b(av+c^2)}{(v^2 + c^2)^{3/2}} e^{-\frac{b^2 (v-a)^2}{2(v^2 + c^2)}} \int\limits_0^q e^{-\frac{t^2}{2}} dt \right] ,$ (3.25)

gde

$q=\frac{b(av+c^2)}{c(v^2 + c^2)^{1/2}} .$ (3.26)

Zavisimost' funkcii L ot A₀, D₀ opredelyaetsya vhodyashimi v (3.25) i (3.26) velichinami a, kotorye svyazany s nimi sootnosheniem (3.24).

Netrudno predstavit' sebe, naskol'ko gromozdko dolzhny vyglyadet' napisannye v yavnom vide uravneniya (3.21). Poetomu v deistvitel'nosti oni ne ispol'zuyutsya. Vmesto etogo Braun predpochitaet, zadavaya ryad menyayushihsya cherez 1 - 2°; vozmozhnyh znachenii A₀, D₀, vychislyat' dlya kazhdoi pary etih znachenii po privedennym vyshe formulam velichinu L. Naidya po hodu etih velichin ih maksimum, mozhno naiti i sootvetstvuyushee naiveroyatneishee znachenie koordinat A₀, D₀.

Original'nyi metod nahozhdeniya rasstoyaniya do dvizhushegosya skopleniya, ne trebuyushii znaniya koordinat verteksa, predlozhil Hercshprung (1919). Metod osnovan na opredelenii godichnogo izmeneniya uglovyh razmerov skopleniya, obuslovlennogo izmeneniem rasstoyaniya mezhdu nim i Solncem.

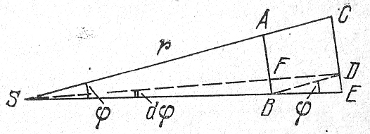
Ris. 14. Shema, poyasnyayushaya vyvod formul (3.27)-(3.30).

Pust' na rasstoyanii r ot Solnca S nahoditsya skoplenie, vidimoe pod uglom φ = &ang ASB (ris. 14). S uvelicheniem rasstoyaniya na velichinu dr = AS ugol φ umen'shaetsya na velichinu dφ. Otrezki AV i CD ravny. Rassmatrivaya treugol'niki SFB i DFB, nahodim:

$-rd\phi = \phi dr.$ (3.27)

Otsyuda

$\frac{d\phi}{\phi dt} = -\frac{dr}{rdt} .$ (3.28)

Tak kak parallaks $\pi = \frac{1}{r}$, to $\frac{d\phi}{\phi} = -\pi V_r dt$ , i dlya opredeleniya π poluchaem formulu

$\pi = -\frac{d\phi}{\phi V_r dt} .$ (3.29)

Vyrazhaya t v godah, a V_r - v km/s, nahodim

$\pi^{\prime\prime} = -\frac{977813}{V_r} \frac{d\phi}{\phi dt} .$ (3.30)

Pri dt, ravnom godu, mnozhitel' V = (dφ)/(φdt) yavlyaetsya otnositel'nym godichnym izmeneniem razmerov skopleniya ili rasstoyanii mezhdu ego chlenami. Naidya ego, opredelyaem π.

Modifikaciei metoda Hercshprunga yavlyaetsya metod opredeleniya gradientov sobstvennyh dvizhenii v oblasti skopleniya, razvityi Aptonom (1970). Ishodnym uravneniem v metode Aptona sluzhit uravnenie (3.28). Tak kak (dφ)/(dt) = dμ_α = dμ_δ, a ugol φ = Δα = Δδ, to v pervom priblizhenii (dlya skoplenii malyh uglovyh razmerov)

$\frac{1}{r}\frac{dr}{dt} = -\frac{d\mu_\alpha}{d\alpha} = -\frac{d\mu_\delta}{d\delta} .$ (3.31)

Zdes' (dr)/(dt) - luchevaya skorost' zvezdy, nahodyasheisya v centre skopleniya, a r - rasstoyanie do etogo centra.

Kak otmechaet Henson (1975), uravneniya Aptona mozhno vyvesti putem differencirovaniya osnovnyh formul vida (1.1), ispol'zuemyh dlya opredeleniya gruppovyh parallaksov. Poskol'ku polozhenie verteksa, po sushestvu, opredelyaetsya razlichiem komponentov sobstvennyh dvizhenii chlenov skopleniya, yasno, chto ono odnoznachno fiksiruetsya gradientami etih dvizhenii v oblasti skopleniya. Poetomu metod Aptona podobno metodu Hercshprunga mozhet rassmatrivat'sya kak tot zhe metod opredeleniya gruppovyh parallaksov, tol'ko zapisannyi v inoi matematicheskoi forme.

Analiz sravnitel'nyh dostoinstv i nedostatkov razlichnyh metodov opredeleniya gruppovyh parallaksov mozhno naiti, v chastnosti, v stat'yah Brauna (1950), Pitri i Moilsa (1953), a takzhe Hensona (1975).

Na opredelenie polozheniya apeksa i rasstoyaniya do skopleniya mogut okazat' vliyanie sistematicheskie vnutrennie dvizheniya zvezd v skoplenii i ego vrashenie, ibo pri etom sobstvennye dvizheniya ryada zvezd ne soidutsya tochno v apekse, a luchevye skorosti otdel'nyh zvezd ne budut proporcional'ny velichine V cosλ. Metodika vyyavleniya i ucheta etih effektov rassmotrena v upomyanutoi vyshe stat'e Veimana i dr. (1965), a takzhe v stat'e Veimana (1967) v svyazi s problemoi utochneniya parallaksa Giad (sm. § 3.14). My ne budem ostanavlivat'sya na etih voprosah, imeyushih v nastoyashee vremya prakticheskoe znachenie lish' dlya odnogo skopleniya.

<< 3.2 Trigonometricheskie, dinamicheskie i spektral'nye parallaksy | Oglavlenie | 3.4 Diagrammy Hercshprunga-Ressela. Opredelenie rasstoyanii do skoplenii po velichinam i spektral'nym klassam zvezd >>

Publikacii s klyuchevymi slovami: zvezdy - Skoplenie Publikacii so slovami: zvezdy - Skoplenie
Sm. takzhe: Chernaya dyra razrushaet zvezdu: animaciya Zvezdy, pyl' i tumannost' v NGC 6559 25 samyh yarkih zvezd na nochnom nebe Animaciya: chernaya dyra razrushaet zvezdu Kometa, skopleniya i tumannosti Sravnenie razmerov zvezd Samaya dalekaya iz vseh izvestnyh zvezd? Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce