Astronet > Zvezdnye skopleniya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Zvezdnye skopleniya << 4.2 Skoplenie Bol'shoi Medvedicy i potok Tel'ca | Oglavlenie | 4.4 O dinamicheskoi ustoichivosti dvizhushihsya skoplenii >>

4.3 Kinematicheskie zvezdnye gruppy

Novyi etap v izuchenii dvizhushihsya zvezdnyh grupp nastupil v 1957 g., kogda Eggen (1957; 1958a; 1965v) nachal sistematicheskoe issledovanie etih sistem. Eggen nachal s izucheniya klassicheskih grupp Giad i Siriusa. Princip, polozhennyi v osnovu vydeleniya chlenov gruppy, yavlyaetsya modifikaciei uzhe izvestnogo metoda opredeleniya gruppovyh parallaksov. V sluchae dvizhushegosya skopleniya nam izvestny sobstvennye dvizheniya ego chlenov i tochka shozhdeniya etih dvizhenii. Dopustim teper', chto nam horosho izvestny rasstoyanie i prostranstvennaya skorost' nekotoroi interesuyushei nas zvezdy, nahodyasheisya v okrestnostyah Solnca. Eto znachit, chto my znaem napravlenie i velichinu vektora skorosti zvezdy. Perenesem ego parallel'no samomu sebe v glaz nablyudatelya. Pri prodolzhenii ego v beskonechnost' on peresechet nebesnuyu sferu v tochke, kotoruyu mozhno nazvat' apeksom dannoi zvezdy, po analogii s apeksom Solnca.

Naidem teper' v okruzhayushem nas okolosolnechnom ob'eme prostranstva zvezdy, kotorye imeyut obshee s dannoi zvezdoi prostranstvennoe dvizhenie. Eti zvezdy i obrazuyut dvizhushuyusya gruppu dannoi zvezdy. Skorost'yu gruppovogo dvizheniya v etom sluchae sluzhit skorost' dannoi zvezdy. Slovo "dvizhushayasya" uzhe davno obychno opuskaetsya. Tochkoi shozhdeniya sobstvennyh dvizhenii chlenov gruppy sluzhit apeks dannoi zvezdy. Takim obrazom, dlya togo chtoby mozhno bylo otnesti nekotoruyu zvezdu k gruppe dannoi zvezdy, nuzhno, chtoby ee sobstvennoe dvizhenie μ, i luchevaya skorost' V_r udovletvoryali opredelennym trebovaniyam, diktuemym usloviyami gruppovogo dvizheniya (sm. § 3.3).

Pust' V_r i θ - luchevaya skorost' i pozicionnyi ugol sobstvennogo dvizheniya nekotoroi zvezdy s ekvatorial'nymi koordinatami α, δ ; θ (A₀, D₀) - pozicionnyi ugol gruppovogo dvizheniya v tochke (α, δ) nebesnoi sfery, gde A₀, D₀ - ekvatorial'nye koordinaty apeksa gruppy; V_r^c - gruppovaya luchevaya skorost' v tochke (α, δ); λ - uglovoe rasstoyanie zvezdy ot apeksa; V - gruppovaya skorost'. Togda V_r^c = V cos λ, a znachenie θ(A₀, D₀) vychislyaetsya po formule (3.14). Rassmatrivaya oshibki opredeleniya vseh etih velichin dlya zvezd skopleniya Giady, Eggen (1958a) prishel k vyvodu, chto odnim iz uslovii dlya otneA₀, D₀, V sluzhit neravenstvo

$\Delta\theta = |\theta-\theta(A_0, D_0)| \le \frac{2^\circ,8}{\sin\lambda},$ (4.1)

a drugim - neravenstvo

$|V_r - V_r^c| \le 3,4 \; \mbox{ili } 5 \mbox{km/s},$ (4.2)

Otobrav takim obrazom vozmozhnye chleny gruppy Giad, Eggen nashel po metodu opredeleniya gruppovyh parallaksov ih rasstoyaniya, a zatem - absolyutnye velichiny, posle chego postroil diagrammu Hercshprunga - Ressela dlya chlenov gruppy. V sostav gruppy Eggen (1957) vklyuchil i skoplenie Yasli, dvizhusheesya v prostranstve so skorost'yu, sovpadayushei so skorost'yu Giad. Vpervye obratil na eto vnimanie vmeste s Hercshprungom eshe K. Shvarcshil'd (1913). V kataloge FK3 okazalos' tol'ko 20 vozmozhnyh chlenov gruppy Giad s izvestnymi luchevymi skorostyami, udovletvoryayushih usloviyam (4.1) i (4.2). Eshe chetyre pribavilos' pri vvedenii vmesto usloviya (4.1) trebovaniya

$2^\circ,8 < \Delta\theta\sin\lambda \le 5^\circ,6.$ (4.3)

32 vozmozhnyh chlena gruppy byli vydeleny Eggenom iz chisla zvezd, nahodyashihsya v predelah 20 ps ot Solnca, po dannym kataloga Glize (1957). Na ris. 61 predstavlena poluchennaya Eggenom (1958a) diagramma M_V, (P - V)_E dlya zvezd gruppy Giad. Ris. 61, po mneniyu Eggena, svidetel'stvuet o fizicheskoi real'nosti razbrosannoi po vsemu nebu gruppy Giad, ibo diagrammy M_V, (R - V)_E dlya chlenov gruppy i chlenov skoplenii Giady i Yasli v obshih chertah shodny, ukazyvaya lish' na to, chto nekotorye chleny gruppy mogut byt' molozhe chlenov skoplenii.

Obrashayas' k potoku Bol'shoi Medvedicy, Eggen (1958a) vyskazyvaet mnenie, chto razrezhennoe "skoplenie Bol'shoi Medvedicy yavlyaetsya, skoree, mestnym sgushennom zvezd potoka, a ne ego yadrom". Vposledstvii, pravda, Eggen (1965a) priznaet za skopleniem pravo na sushestvovanie kak samostoyatel'noi chasti potoka. Eggen predpochitaet nazyvat' etot potok gruppoi Siriusa, opirayas' pri otbore vozmozhnyh chlenov gruppy ne na polozhenie sravnitel'no ploho opredelyaemogo radianta skopleniya, a na apeks Siriusa. Pol'zuyas' v etom sluchae kriteriyami

$|\theta-\theta(A_0, D_0)| < \frac{10^\circ}{\sin\lambda}.$ (4.4)

i

$|V_r - V_r^c| \le 5,6 \; \mbox{ili } 7 \mbox{km/s},$ (4.5)

analogichnymi kriteriyam (4.1) i (4.2), Eggen vydelyaet iz chisla zvezd, rassmatrivavshihsya v rabote Roman (1949), 58 vozmozhnyh chlenov gruppy Siriusa, sredi kotoryh nahodyatsya i yarkie chleny skopleniya Bol'shoi Medvedicy. Diagramma M_V, (R - V)_E, poluchennaya Eggenom (1958a) dlya zvezd etoi gruppy, pokazana na ris. 62. Krestikami otmecheny zvezdy, kotorye vypadayut iz obshego hoda tochek, harakterizuyushih, po mneniyu Eggena, sostav gruppy. K chlenam gruppy Eggen otnosit zvezdy, obrazuyushie uzkuyu glavnuyu posledovatel'nost', i kompaktnuyu gruppu zheltyh gigantov s M_V ≈ 0 i (R - V)_E ≈ +0^m,8. Ostal'nye zvezdy mogut ne otnosit'sya k gruppe, sluchaino dvigayas' v napravlenii ee dvizheniya s toi zhe skorost'yu.

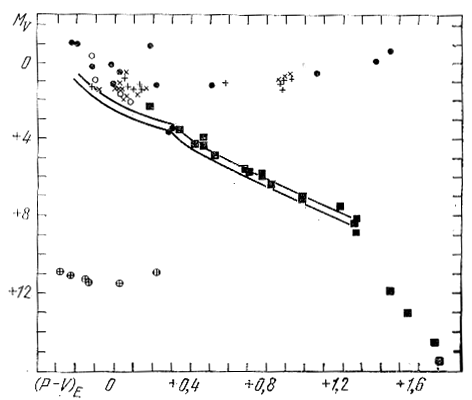
Ris. 61. Diagramma M_V, (R - V)_E chlenov gruppy Giad (Eggen, 1958a). Chernye kruzhki - chleny gruppy, udovletvoryayushie usloviyam (4.1) i (4.2), svetlye kruzhki - usloviyam (4.3) i (4.2). Krestiki i plyusf - yarchaishie chleny skopleniya Giady i Yasli sootvetstvenno. Chernye kvadraty - vozmozhnye chleny iz chisla blizhaishih zvezd. Kruzhki s krestikami - belye karliki. Dvoinoi liniei namechena "standartnaya" glavnaya posledovatel'nost' (Eggen, 1955).

Skorosti dvizheniya grupp Siriusa i Giad otnositel'no Solnca sravnitel'no neveliki (18,4 i 44,0 km/s sootvetstvenno). Issledovav eti gruppy, Eggen (1958b) obratilsya k sostavlennomu im spisku 700 zvezd s vysokimi skorostyami s tem, chtoby vyyavit' vozmozhnye dvizhushiesya gruppy sredi etih ob'ektov.

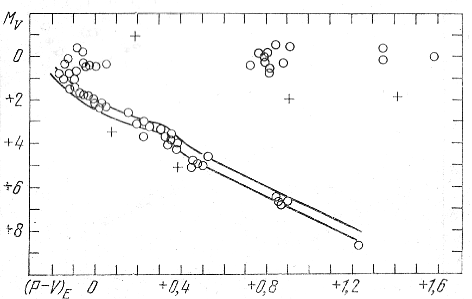
Ris. 62. Diagramma M_V, (R - V)_E chlenov gruppy Siriusa (Eggen, 1958a).

Rassmotrev tri zvezdy s bol'shimi parallaksami (ζ Her, ε Ind i 61 Cyg), imeyushie nadezhno opredelennye prostranstvennye skorosti otnositel'no Solnca (74,5, 88,5 i 108,0 km/s), Eggen vyyavil svyazannye s etimi zvezdami dvizhushiesya zvezdnye gruppy, sostoyashie sootvetstvenno iz 23, 15 i 16 chlenov. Po ocenke Eggena, k kazhdoi gruppe moglo byt' otneseno ne bolee dvuh-treh sluchaino dvizhushihsya s ee skorost'yu zvezd polya. Takim obrazom, gruppa 61 Cyg vnov' vozrodilas', kak Feniks iz pepla. Na ris. 63 (Eggen, 1958b) predstavlena diagramma M_V, (R - V)_E chlenov etih grupp, ochen' pohozhaya na podobnuyu diagrammu chlenov starogo rasseyannogo skopleniya M 67 (sm. dalee ris. 147).

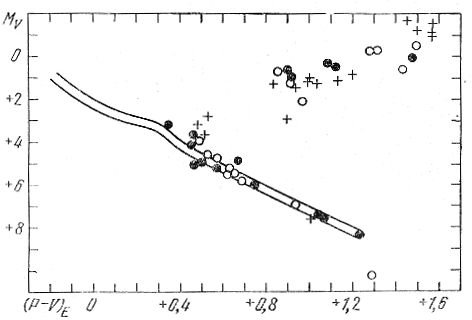
Ris. 63. Diagramma M_V, (R - V)_E dlya zvezd grupp ζ Her (krestiki), ε Ind (svetlye kruzhki) i 61 Cyg (chernye kruzhki) soglasno Eggenu (1958b).

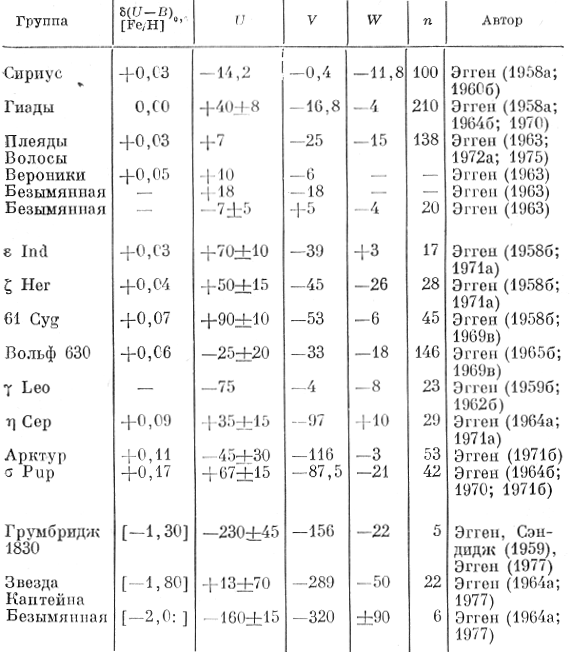
V ryade posleduyushih rabot Eggen (1959a, b; 1964a, b; 1965a, b, v) prodolzhal issledovanie uzhe rassmotrennyh i poiski novyh zvezdnyh grupp, svedeniya o kotoryh privedeny v tabl. 4.1. V pervom stolbce tablicy soderzhitsya nazvanie gruppy; vo vtorom - znachenie ul'trafioletovogo izbytka δ(U - B)_0,6 zvezd gruppy (sm. § 6.3) ili (v kvadratnyh skobkah) znachenie [Fe/H], yavlyayushiesya ukazatelyami soderzhaniya metallov u chlenov gruppy - vazhnogo dopolnitel'nogo kriteriya, ispol'zuemogo dlya otbora etih chlenov; v tret'em, chetvertom i pyatom stolbcah - vyrazhennye v km/s znacheniya komponentov prostranstvennoi skorosti chlenov gruppy, napravlennyh sootvetstvenno ot galakticheskogo centra v ploskosti Galaktiki (U), v napravlenii galakticheskogo vrasheniya v toi zhe ploskosti (V) i k severnomu polyusu Galaktiki (W). V shestom stolbce privoditsya chislo chlenov gruppy (n), v sed'mom - ssylka na osnovnye raboty, posvyashennye issledovaniyam gruppy.

Tablica 4.1

Perehod ot komponentov prostranstvennyh skorostei, vyrazhennyh v ekvatorial'noi sisteme koordinat, k imeyushim bolee yasnyi fizicheskii smysl galakticheskim komponentam U,V,W, otrazhayushim osobennosti dvizheniyam zvezd v prostranstve po ih galaktocentricheskim orbitam, pokazal, chto dvizheniya chlenov grupp v napravlenii, perpendikulyarnom k galakticheskoi ploskosti (W), mogut byt' nezavisimy ot U- i V-komponentov ih skorostei. Schitaya, chto chleny gruppy imeyut obshee proishozhdenie, mozhno dopustit', chto oni sohranyayut dispersiyu skorostei, prisushuyu im posle ih obrazovaniya v nekotorom pervonachal'nom ob'eme diffuznogo oblaka, obrashavshegosya vokrug galakticheskogo centra. Kak otmetil Vulli (1961), nablyudatel', registriruyushii v okrestnostyah Solnca ogromnuyu rasseyannuyu gruppu zvezd, imeyushih obshee proishozhdenie, vidit lish' vyborku iz pervonachal'noi gruppirovki, a imenno tol'ko te ee chleny, kotorye k momentu nablyudeniya okazalis' v tom ob'eme galakticheskogo prostranstva, cherez kotoryi v eto vremya prohodit Solnce; zvezdy, obrazuyushie etu vyborku, neizbezhno dolzhny obladat' odinakovym znacheniem komponenta V skorosti, s kotoroi oni obrashayutsya vokrug galakticheskogo centra. Pri etom oni mogut imet' zametnuyu dispersiyu U- i W-komponentov ih skorostei, pri uslovii, chto v processe dvizheniya oni ostayutsya vblizi nekotoroi srednei orbity nachal'nogo oblaka. Dispersiya W-komponentov skorostei chlenov gruppy zavisit po tol'ko ot pervonachal'noi dispersii etih skorostei (obuslovlivayushei razlichiya U-komponentov), po i ot razmerov nachal'nogo oblaka i ego polozheniya otnositel'no galakticheskoi ploskosti.

Ishodya iz etih soobrazhenii, uzhe s 1960 g. Eggen (1960a) prinyal sleduyushuyu proceduru otbora vozmozhnyh chlenov gruppy Giad. Snachala iz spiska zvezd polya otbirayutsya vse zvezdy s dovol'no bol'shimi znacheniyami raznostei θ - θ(A₀, D₀) i V_r - V_c (sm. formuly (4.1) - (4.3)). Dlya etih zvezd s pomosh'yu priemlemyh znachenii fotometricheskih parallaksov, sootvetstvuyushih spektral'nym klassam zvezd, nahodyatsya komponenty vektorov prostranstvennyh skorostei U, V, W. Esli dlya lyubogo iz dopustimyh znachenii parallaksa poluchayushiesya znacheniya U i V sovpadayut v zadannyh predelah s prinyatymi znacheniyami U- i V-komponentov prostranstvennoi skorosti Giad, dannaya zvezda vydelyaetsya v kachestve kandidata v vozmozhnye chleny gruppy. Znachenie komponenta W pri etom sovershenno ignoriruetsya. Zatem po obychnoi formule (1.1) vychislyaetsya gruppovoi parallaks dannoi zvezdy i utochnyayutsya znacheniya U-, V-komponentov ee skorosti. Po znacheniyam M_V, naidennym s pomosh'yu gruppovyh parallaksov, zvezdy nanosyatsya na diagrammu (M_V, pokazatel' cveta), postroennuyu dlya chlenov skopleniya Giady. Zvezda schitaetsya chlenom gruppy, esli ona popadaet v zadannye predely lyuboi posledovatel'nosti, nablyudaemoi na etoi diagramme.

Na postroennoi Eggenom (1960a) diagramme M_V, (B - V)_E chlenov gruppy Giad, vydelennyh takim obrazom, obrashaet na sebya vnimanie vozmozhnaya prinadlezhnost' k etoi gruppe peremennoi δ Shita, yavlyayusheisya prototipom sootvetstvuyushego tipa peremennyh zvezd. Gruppa vytyanuta v napravlenii galakticheskogo vrasheniya. Polovina chlenov gruppy - dvoinye i kratnye sistemy. Mezhdu |z|-koordinatami i znacheniyami |W| zvezd gruppy Giad sushestvuet zametnaya korrelyaciya. Zvezdy s bol'shimi znacheniyami |z| imeyut malye |W|. V dal'neishem oni dolzhny nachat' padat' k galakticheskoi ploskosti s vozrastayushei skorost'yu, dostigaya maksimuma skorosti |W| pri peresechenii etoi ploskosti.

Pri povtornom izuchenii gruppy Siriusa Eggen (1960b) prinyal neskol'ko inuyu proceduru otbora chlenov gruppy, chem v sluchae gruppy Giad, poskol'ku dvizhenie po z-koordinate u Siriusa sravnimo po velichine s polnoi prostranstvennoi skorost'yu gruppy. My opishem etu proceduru, stavshuyu osnovnoi vo vseh posleduyushih podobnyh rabotah Eggena, chtoby pokazat', k kakim uhishreniyam prihoditsya pribegat' issledovatelyam dvizhushihsya grupp zvezd, otkazyvayushimsya ot strogih ogranichenii klassicheskogo metoda gruppovyh parallaksov, nakladyvaemyh na prostranstvennye skorosti zvezd trebovaniem ravenstva vektorov etih skorostei.

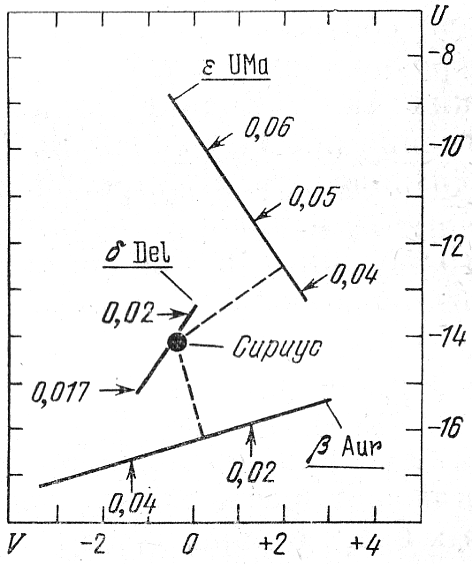
Ris. 64. Chast' ploskosti (U, V), soderzhashaya Sirius i tri vozmozhnyh chlena ego gruppy (Eggen, 1960b).

V svyazi s etim, v dal'neishem my budem nazyvat' gruppy zvezd, vydelyaemye v prostranstve skorostei po priznaku obshnosti kakogo-libo iz komponentov vektorov ih skorostei, kinematicheskimi zvezdnymi gruppami, chtoby otlichat' ih ot dvizhushihsya skoplenii i grupp, u kotoryh dolzhny byt' odinakovy vektory skorostei ih chlenov.

Na ris. 64 (Eggen, 1960b) izobrazhena chast' ploskosti (U, V), soderzhashaya Sirius i tri vozmozhnyh chlena ego gruppy - ε UMa, β Aur i δ Del. Strelkami pokazany tochki, sootvetstvuyushie razlichnym znacheniyam parallaksov etih zvezd, dayushim sootvetstvuyushie znacheniya komponentov U, V ih skorostei. V sluchae dvizhushihsya skoplenii pryamye na ploskosti (U, V), sootvetstvuyushie chlenam skoplenii, dolzhny prohodit' cherez odnu tochku.

Za vozmozhnye chleny gruppy Siriusa Eggen prinimaet te zvezdy, kratchaishie rasstoyaniya geometricheskih mest raspolozheniya komponentov U, V kotoryh ot tochki, sootvetstvuyushei polozheniyu Siriusa, ne prevyshayut 4 km/s. Eti rasstoyaniya pokazany na ris. 64 preryvistymi liniyami. Znacheniya parallaksom, sootvetstvuyushie etim rasstoyaniyam, i prinimayutsya Eggenom za znacheniya gruppovyh parallaksov rassmatrivaemyh zvezd, ne zavisyashie ot znachenii W-komponeitov ih skorostei. Takim putem Eggenu udalos' prichislit' k gruppe Siriusa uzhe 100 chlenov, v tom chisle δ Del, peremennuyu tipa δ Shita.

Ispol'zovanie ploskosti (U, V) pozvolyaet obnaruzhivat' kinematicheskie gruppy po mestam koncentracii na nei sootvetstvuyushih tochek. Prakticheski vse gruppy, perechislennye v tabl. 4.1, pereshli v razryad kinematicheskih po metodike vydeleniya ih vozmozhnyh chlenov. Imenno poetomu znacheniya U, privedennye v etoi tablice, dlya ryada grupp soprovozhdayutsya ukazaniem predelov vozmozhnyh razlichii U-komponentov chlenov dannoi gruppy. Privedennye v toi zhe tablice znacheniya W-komponentov ob'ektov, olicetvoryayushih kinematicheskie gruppy, po suti dela dlya dannoi gruppy sluchainy i dlya otdel'nyh ee chlenov mogut razlichat'sya v ochen' shirokih predelah.

Gruppy v tabl. 4.1 raspolozheny v poryadke umen'sheniya soderzhaniya metallov i razbity na tri chasti. Pervaya vklyuchaet shest' grupp, sostoyashih iz sravnitel'no molodyh zvezd s normal'nym i vysokim soderzhaniem tyazhelyh elementov i diagrammami M_V, V - V, podobnymi diagrammam Pleyad i Giad. Eggen otnosit ih k molodomu naseleniyu diska Galaktiki. Vosem' grupp vtoroi chasti tablicy (s neskol'ko men'shim, v srednem, soderzhaniem metallov) mozhno otnesti k staromu naseleniyu diska. Diagrammy M_V, V - V ih chlenov, kak my uzhe videli, napominayut diagrammy staryh rasseyannyh skoplenii vrode M 67. Nakonec, tri poslednie gruppy, nesomnenno, otnosyatsya k sfericheskoi sostavlyayushei Galaktiki, i diagrammy M_V, V - V ih chlenov shodny s analogichnymi diagrammami zvezd sharo-yh skoplenii, sm. ris. 65 (Eggen, 1977), na kotorom pokazany diagrammy M_V, V - V dlya chlenov gruppy zvezdy Kapteina i dlya sharovogo skopleniya M 3.

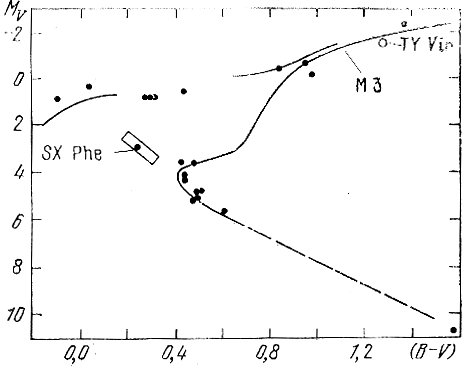
Ris. 65. Diagramma M_V, V - V dlya chlenov gruppy zvezdy Kapteina (tochki) i sharovogo skopleniya M 3 (Eggen, 1977).

My uzhe znaem, chto v gruppu Giad vhodyat dva rasseyannyh skopleniya - Giady i Yasli, shodnye po vozrastu i mnogim drugim fizicheskim harakteristikam, skopleniya-bliznecy. K gruppe Siriusa, soderzhashei skoplenie Bol'shoi Medvedicy, Lloid Ivens i Midous (1964) otnesli po kinematicheskim priznakam skoplenie NGC 7092 (M 39), diagramma M_V, V - V kotorogo sovpadaet s diagrammoi skopleniya Bol'shoi Medvedicy. Znacheniya komponentov skorostei U, V i W dlya skopleniya NGC 7092 ravny sootvetstvenno -20 ± 3, +1 ± 3 i -11 ± 3 km/s. Etot vyvod podtverdil i Eggen (1965v).

Odnovremenno i vsled za etim Eggen (1964v; 1965v; 1974) otnes bol'shoe chislo molodyh rasseyannyh skoplenii, perechislennyh v tabl. 4.2, k gruppe Pleyad. V stolbce r tabl. 4.2 my privodim rasstoyaniya etih skoplenii ot Solnca v shkale Eggena, poskol'ku imenno na etih znacheniyah r osnovany privedennye v toi zhe tablice velichiny U, V, W dlya skoplenii etoi kinematicheskoi gruppy. Tri poslednih skopleniya v tabl. 4.2 Eggen (1974) schitaet lish' vozmozhnymi chlenami gruppy.

Tablica 4.2

Skoplenie	r(ps)	U	V	W	Avtor
Pleyady	129	+7	-25	-15	Eggen(1964v; 1965v;1974; 1975)
α Per	178	+14	-25	-6	Eggen(1964v; 1965v;1974a; 1974)
NGC 2516	445	+24	-26	+7	Eggen(1964v; 1965v;1974a; 1974)
IC 2602	151	+4	-27	+3	Eggen(1964v; 1965v;1974a; 1974)
NGC 1039	440	+3	-27	-20	Eggen(1964v)
δ Lyr	316	+15	-24	+1	Eggen(1968b;1972a; 1974)
NGC 2287	759	(+21)	(-26)	(-6)	Eggen(1971g;1972a; 1974)
Cr 121	500	(+25)	(-25)	(-15)	Eggen(1974)
NGC 6885	417	(+2)	(-25)	(-11)	Eggen(1974)

Skopleniya, vhodyashie v gruppu Pleyad, zanimayut ogromnyi ob'em prostranstva. Esli uchest', chto chast' zvezd iz gruppirovki Skorpiona - Centavra takzhe prichislyaetsya Eggenom (1972a) k gruppe Pleyad, to stanet yasno, chto k etoi gruppe Eggen otnosit ochen' bol'shuyu dolyu molodyh skoplenii Poyasa Gulda, t. e. Mestnoi sistemy, kotoruyu Eggen (1975) nazyvaet mestnoi associaciei. Eggen voobshe dopuskaet vozmozhnost' togo, chto "ves' kompleks Poyasa Gulda voznik iz odnogo gazovogo oblaka, dvigavshegosya vokrug centra Galaktiki", i otnosit k mestnoi associacii ryad T-associacii, nablyudaemyh v temnyh tumannostyah sozvezdii Tel'ca, Hameleona, Volka. Sudya po diagrammam M_bol, lgT_e dlya zvezd gruppy Pleyad, opublikovannym Eggenom (1972a; 1975), vidno, chto v etom sluchae im dopuskaetsya zametnoe razlichie vozrastov chlenov gruppy (v predelah ot 1 · 10⁷ do 8 · 10⁸ let).

Mnogie (sm., naprimer, Benedikt Arnol'd, 1974) somnevayutsya v real'nosti grupp Eggena. Sredi mnozhestva zvezd raznogo vozrasta i himicheskogo sostava, dvizhushihsya v okrestnostyah Solnca v raznyh napravleniyah i s raznymi skorostyami, vsegda mozhno podobrat' nekotoroe chislo ob'ektov, kotorye budut imet' zadannye skorosti i okazhutsya na takih rasstoyaniyah ot Solnca, chto sootvetstvuyushie im tochki raspolozhatsya na diagramme M_V, V - V vdol' zadannyh posledovatel'nostei, harakter kotoryh netrudno predvidet'. V svyazi s etim, sleduet s bol'shoi ostorozhnost'yu otnosit'sya k rezul'tatam ispol'zovaniya zvezdnyh grupp dlya opredeleniya svetimosti redko vstrechayushihsya ob'ektov, kotorye zachislyayutsya v eti gruppy (obychno, imi okazyvayutsya yarkie peremennye zvezdy). My uzhe upominali o neskol'kih peremennyh, prichislennyh k gruppam Giad i Siriusa. Eggen otnosit k gruppe Pleyad cefeidu α UMi, peremennuyu tipa δ Shita DY Peg - k gruppe σ Pup, a R CrB - k gruppe Vol'f 630. K gruppe Grumbridzh 1830 byla otnesena sama RR Lyr, mediannaya absolyutnaya velichina kotoroi M_V pri pervom opredelenii okazalas' ravnoi +0^m,6. Pozzhe Eggen (1977) nashel dlya nee novoe znachenie M_V = +0^m,35.

Naibol'shee chislo peremennyh otneseno k gruppe zvezdy Kapteina (sm. ris. 65): zdes' i peremennye tipa RR Liry, SU Dra, U Lep, X Ari, ST Leo, mediannye absolyutnye velichiny Mv kotoryh, poluchennye po gruppovym parallaksam etih zvezd, zaklyucheny v predelah ot +0^m,6 do +0^m,85, i polupravil'naya TY Vir, i zamechatel'naya peremennaya SX Phe, pul'siruyushaya s periodom 0^d,055.

Trudno, odnako, otdelat'sya ot mysli o tom, chto vse perechislennye peremennye vryad li byli by otneseny k rassmatrivaemym zvezdnym gruppam, esli by ih absolyutnye velichiny, osnovannye na gruppovyh parallaksah, sushestvenno otlichalis' ot nashih sovremennyh predstavlenii o znacheniyah etih velichin.

I tem ne menee vse eto ne tak prosto. Zvezdnye skopleniya voznikayut ne v pustom prostranstve i v svoem dvizhenii po galakticheskim orbitam mogut soprovozhdat'sya zvezdami, voznikshimi pochti odnovremenno s nimi v ih shirokih okrestnostyah. V takom sluchae zvezdnye gruppy mogut byt' real'nymi fizicheskimi sistemami. No mogut li oni sohranyat'sya v Galaktike na protyazhenii dlitel'nyh promezhutkov vremeni? Dlya resheniya etogo voprosa neobhodimo obratit'sya k teorii differencial'nogo vrasheniya Galaktiki.

<< 4.2 Skoplenie Bol'shoi Medvedicy i potok Tel'ca | Oglavlenie | 4.4 O dinamicheskoi ustoichivosti dvizhushihsya skoplenii >>

Publikacii s klyuchevymi slovami: zvezdy - Skoplenie Publikacii so slovami: zvezdy - Skoplenie
Sm. takzhe: Chernaya dyra razrushaet zvezdu: animaciya Zvezdy, pyl' i tumannost' v NGC 6559 25 samyh yarkih zvezd na nochnom nebe Animaciya: chernaya dyra razrushaet zvezdu Kometa, skopleniya i tumannosti Sravnenie razmerov zvezd Samaya dalekaya iz vseh izvestnyh zvezd? Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce