Astronet > Zvezdnye skopleniya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Zvezdnye skopleniya << 6.3 Obshii vid diagramm velichina - pokazatel' cveta zvezd sharovyh skoplenii. Zvezdy glavnoi posledovatel'nosti v etih sistemah i subkarliki | Oglavlenie | 6.5 Spektry yarkih zvezd sharovyh skoplenii. Soderzhanie tyazhelyh elementov v ih atmosferah >>

6.4 Problema opredeleniya rasstoyanii do sharovyh skoplenii. Problema subkarlikov

Pri opredelenii rasstoyanii do sharovyh skoplenii s pomosh'yu glavnyh posledovatel'nostei etih sistem my, ochevidno, stalkivaemsya s temi zhe problemami, kotorye uzhe byli rassmotreny ranee v §§ 3.11-3.15 v svyazi s opredeleniem rasstoyanii do skoplenii rasseyannyh. Eto problemy ucheta evolyucionnyh effektov, ucheta razlichii v soderzhanii tyazhelyh elementov (a takzhe, vozmozhno, i geliya) i opredeleniya nachal'noi glavnoi posledovatel'nosti dlya zvezd s malym soderzhaniem metallov.

Posle togo kak bylo vyyasneno, chto nachal'naya glavnaya posledovatel'nost' zvezd s nizkim soderzhaniem metallov na diagramme M_V, V - V posle ucheta pokrovnogo effekta dolzhna sovpast' s nachal'noi glavnoi posledovatel'nost'yu zvezd s vysokim soderzhaniem metallov (posledovatel'nost'yu Giad), vopros o vybore nachal'noi glavnoi posledovatel'nosti zvezd sharovyh skoplenii schitalsya reshennym. Dlya sovmesheniya s neyu glavnyh posledovatel'nostei sharovyh skoplenii (posle vneseniya v nih popravok za pokrovnyi effekt) ostavalos' uchest' izmenenie ee formy, obuslovlennoe evolyucionnymi effektami.

V § 3.11 opisan metod Dzhonsona (1960) opredeleniya rasstoyanii do rasseyannyh skoplenii, osnovannyi pa ispol'zovanii krivoi evolyucionnyh otklonenii. Tam zhe izlozheny rezul'taty primeneniya etogo metoda Sendidzhem (1962a) dlya nahozhdeniya rasstoyanii do ochen' staryh rasseyannyh skoplenii. Posle vsego skazannogo yasno, chto takim zhe obrazom mozhno opredelyat' rasstoyaniya i do sharovyh skoplenii. Sleduet uchest' tol'ko, chto v poslednem sluchae nuzhno pol'zovat'sya ne krivoi evolyucionnyh otklonenii dlya zvezd "tipa I" (sm. tabl. 3.5), a krivoi evolyucionnyh otklonenii dlya zvezd "tipa IIa" (X = 0,99, Y = 0,009) ili "IIb" (X = 0,75, Y = 0,249), tak kak formy etih krivyh razlichny.

Ispol'zuya krivuyu evolyucionnyh otklonenii dlya zvezd "tipa IIa" Sendidzh (1962a, b) opredelil rasstoyaniya do sharovyh skoplenii M 3, M 5, M13, schitaya, chto izbytki cveta etih sistem ravny nulyu. Pa ris. 86 (Sendidzh, (1962a) pokazano raspolozhenie osnovnyh posledovatel'nostei etih skoplenii i staryh rasseyannyh skoplenii M 67 i NGC 188 na diagramme M_Vc, (V - V)_c, gde indeks s oznachaet, chto sootvetstvuyushie velichiny ispravleny za pokrovnyi effekt. No zdes' my dolzhny obratit' vnimanie na to, chto nanesennoe na ris. 85 sploshnoi liniei polozhenie glavnoi posledovatel'nosti Giad osnovano na prinimavshemsya Eggenom i Sendidzhem (1962) znachenii modulya rasstoyaniya Giad 3^m,1. Uvelichivaya eto znachenie na 0^m,2 (sm. § 3.14), sleduet priznat', chto uchet pokrovnogo effekta ne mozhet privesti polozheniya "ekstremal'nyh" subkarlikov na ris. 85 na novuyu nachal'nuyu glavnuyu posledovatel'nost' zvezd s vysokim soderzhaniem metallov (sm. § 3.15), izobrazhennuyu na ris. 85, b preryvistoi liniei, dazhe esli dopustit' (Eggen, 1971v; 1973), chto eti subkarliki za vremya sushestvovaniya Galaktiki zametno proevolyucionirovali i smestilis' na diagramme M_V, V - V - vpravo za schet evolyucionnyh effektov.

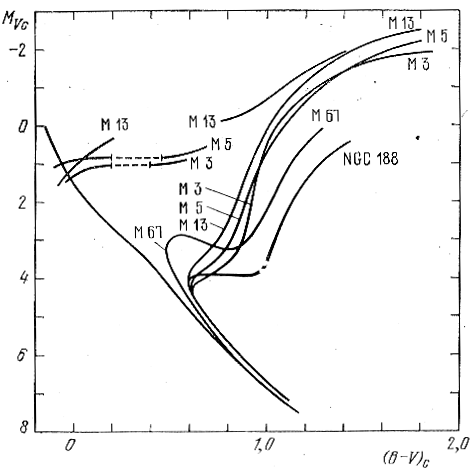
Ris. 86. Polozhenie osnovnyh posledovatel'nostei staryh skoplenii M 3, M 5, M 13, M 67 i NGC 188 na diagramme M_Vc, (V - V)_c s uchetom pokrovnogo effekta i evolyucionnyh effektov (Sendidzh, 1962a).

Eshe Folkner (1967) pokazal, chto dlya ob'yasneniya nablyudaemoi shiriny glavnoi posledovatel'nosti neobhodimo prinyat', chto u subkarlikov v moment ih obrazovaniya Y ≈ 0,20. Takim obrazom, nuzhno schitat', chto nachal'naya glavnaya posledovatel'nost' na diagramme M_bol, lgT_e obladaet zametnoi shirinoi, ochevidno, potomu, chto soderzhanie geliya v zvezdah s malym soderzhaniem metallov bol'she, chem dopuskali v svoe vrem Hazel'grov i Hoil (1959). Pri etom vdol' verhnei granicy nachal'noi glavnoi posledovatel'nosti raspolagayutsya zvezdy s vysokim soderzhaniem metallov, vdol' nizhnei - s nizkim. Uchet pokrovnogo effekta, kak pokazyvaet ris. 85, ne ustranyaet shiriny nachal'noi glavnoi posledovatel'nosti i na diagramme M_V, V - V.

Eto obstoyatel'stvo znachitel'no uslozhnyaet problemu tochnogo opredeleniya rasstoyanii do sharovyh skoplenii. Sovershenno ochevidno, chto teper' my vynuzhdeny dopustit' sushestvovanie celogo semeistva nachal'nyh glavnyh posledovatel'nostei na diagramme M_V, V - V, zavisyashego ot soderzhaniya geliya Y i soderzhaniya metallov Z. S etim semeistvom dolzhno byt' odnoznachno svyazano i semeistvo sootvetstvuyushih krivyh evolyucionnyh otklonenii.

K schast'yu, shirina glavnoi posledovatel'nosti ΔM_V posle ucheta pokrovnogo effekta vryad li prevyshaet 0^m,9 tak chto primenenie opisannoi vyshe metodiki vse zhe pozvolit nadeyat'sya pa opredelenie modulei rasstoyaniya sharovyx skoplenii s tochnost'yu do neskol'kih desyatyh zvezdnoi velichiny. V samom dele, esli dopustit', naprimer, sleduya Eggenu i Sendidzhu (1962), chto zvezdy glavnoi posledovatel'nosti skopleniya M 13 podobny "ekstremal'nym" subkarlikam, izobrazhennym na ris. 85, a, - chto pravdopodobno, ibo srednie znacheniya δ(U - V) dlya zvezd v M 13 i etih subkarlikov ravny +0^m,23 i +0^m,21 sootvetstvenno, - to mozhno neposredstvenno sovmestit' glavnuyu posledovatel'nost' M 13 s posledovatel'nost'yu "ekstremal'nyh" subkarlikov, prinimaemuyu v dannom sluchae zastandartnuyu, ne pribegaya k procedure pokrovnogo effekta. Rezul'taty takogo sovmesheniya pokazany na ris. 87 (Eggen, Sendidzh, 1962). Pri etom modul' rasstoyaniya M 13 okazyvaetsya ravnym 14^m,30. Ranee, pol'zuyas' metodom, osnovannym na uchete pokrovnogo effekta, Sendidzh (1962a, b) poluchil dlya M 13 znachenie m - M = 14^m,43 (sm. ris. 86).

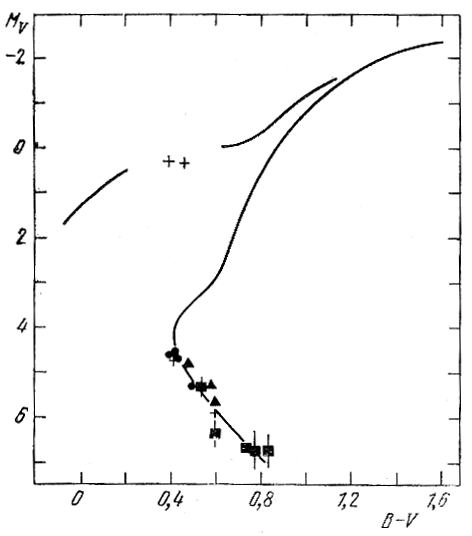
Ris. 87. Sovmeshenie glavnoi posledovatel'nosti skopleniya M 13 na diagramme M_V, V - V so "standartnoi" glavnoi posledovatel'nost'yu "ekstremal'nyh" subkarlikov s δ(U - V) ≥ 0^m,16 (Eggen, Sendidzh, 1962).

V 1970 g, Sendidzh razrabotal novyi metod opredeleniya rasstoyanii do staryh zvezdnyh skoplenii, osnovannyi na ispol'zovanii zavisimosti mezhdu absolyutnymi velichinami i ul'trafioletovymi izbytkami δ(U - V) karlikov i subkarlikov, vpervye obnaruzhennoi Eggenom i Sendidzhem (1962). Sendidzh razbil vse zvezdy polya s izvestnymi π_tr > 0",035 po velichine prisushego kazhdoi iz nih znacheniya δ(0,6) pa chetyre gruppy (A, B, C, D), princip obrazovaniya kotoryh poyasnen v tabl. 6.2 (Sendidzh, 1970).

Tablica 6.2

Gruppa	<δ(0,6)>	<ΔM_V>	n
A(-0^m,05 ≤ δ(0,6) ≤ 0^m,05) B(0^m,06 ≤ δ(0,6) ≤ 0^m,10) C(0^m,11 ≤ δ(0,6) ≤ 0^m,15) D(δ(0,6) ≥ 0^m,16)	0^m,009 0^m,076 0^m,132 0^m,218	-0^m,06 ± 0^m,03 0^m,17 ± 0^m,04 0^m,56 ± 0^m,08 1^m,22 ± 0^m,12	56 36 16 9

Tablica 6.3

B - V	M_V
0^m,45	3^m,78
0^m,50	4^m,10
0^m,55	4^m,45
0^m,60	4^m,78
0^m,65	5^m,02
0^m,70	5^m,32
0^m,75	5^m,60
0^m,80	5^m,85
0^m,85	6^m,10
0^m,90	6^m,34
0^m,95	6^m,58

Dlya kazhdoi zvezdy po izvestnym znacheniyam V i π_tr byla vychislena absolyutnaya velichina M_V, a zatem obrazovany raznosti ΔM_V mezhdu M_V i absolyutnoi velichinoi M_{_V}⁰, V - V tochki na nekotoroi opornoi posledovatel'nosti s pokazatelem cveta V - V, ravnym pokazatelyu cveta dannoi zvezdy. V kachestve opornoi Sendidzh prinyal glavnuyu posledovatel'nost' zvezd, vhodyashih v sostav starogo naseleniya diska Galaktiki. Forma etoi posledovatel'nosti, privedennoi v tabl. 6.3 dlya prakticheski ispol'zuemyh znachenii V - V, sovpadaet so srednei formoi nablyudaemyh glavnyh posledovatel'nostei v skopleniyah M 3, M 13, M 15 i M 92, osvobozhdaya nas ot neobhodimosti dopolnitel'nogo ucheta evolyucionnyh effektov. Udivlenie mozhet vyzvat' tol'ko to obstoyatel'stvo, chto etot otrezok opornoi posledovatel'nosti sovpadaet s otrezkom nachal'noi glavnoi posledovatel'nosti Eggena (1965g).

Znacheniya ΔM_V korreliruyut s δ(0,6). Srednie znacheniya <δ(0,6)> , <ΔM_V> dlya grupp A, V, S, D privedeny v tabl. 6.2. V stolbce n ukazano chislo znead v kazhdoi gruppe. Zavisimost' mezhdu <ΔM_V> i <δ(0,6)> predstavlena sploshnoi liniei pa ris. 88 (Cendidzh, 1970). O svetlom kruzhke na etom risunke my skazhem nemnogo pozzhe.

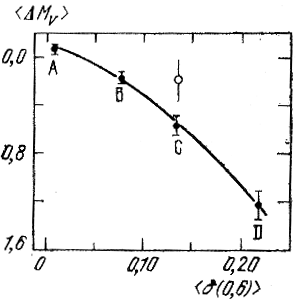
Ris. 88. Zavisimost' mezhdu znacheniyami <ΔM_V> i <δ(0,6)> dlya subkarlikov s π_tr > 0",035 (Sendidzh, 1970).

Opredeliv dlya zvezd glavnoi posledovatel'nosti rassmatrivaemogo skopleniya posle ucheta mezhzvezdnogo poglosheniya sveta srednie znacheniya <(V - V)₀> i <δ(U - V)>, mozhno naiti po tablice Sendidzha (1969b) znachenie <δ(0,6)> etih zvezd, a s pomosh'yu ris. 88 - sootvetstvuyushee emu znachenie <ΔM_V> . Iskomyi modul' rasstoyaniya skopleniya opredelyaetsya teper' vyrazheniem

$V( \langle (B-V)_0 \rangle ) - M_V^0( \langle (B-V)_0 \rangle ) - \langle \Delta M_V\rangle ,$ (6.2)

gde V(<(V - V)₀>) - vidimaya velichina zvezd glavnoi posledovatel'nosti skopleniya, sootvetstvuyushaya <(V - V)₀> .

Dlya sravneniya otmetim, chto naidennyi takim obrazom Sendidzhem (1970) modul' rasstoyaniya skopleniya M 13 okazalsya ravnym 14^m,52, a srednie absolyutnye velichiny <M_V> peremennyh tipa RR Liry v skopleniyah M 3, M 15 i M 92 sootvetstvenno ravnymi +0^m,60, +0^m,98 i +0^m,91.

Etot metod ne zavisit ot tochnosti opredeleniya opornoi posledovatel'nosti (pri vybore drugoi posledovatel'nosti prosto izmenyatsya poluchaemye znacheniya <ΔM_V> . K sozhaleniyu, tochnost' ego vsecelo opredelyaetsya nebol'shim chislom subkarlikov polya s δ(0,6) ≥ +0^m,11 i π_tr > 0",035, a takzhe nebol'shoi tochnost'yu opredeleniya ih parallaksov.

Poskol'ku poluchennye opisannym metodom svetimosti peremennyh tipa RR Liry v skopleniyah M 15 i M 92, otnosyashihsya k II tipu Oosterhofa, okazalis' men'she svetimosti peremennyh v M 3 (skopleniya I tipa Oosterhofa), vopreki vere i ozhidaniyam Sendidzha (sm. § 5.2), Sendidzh reshil, chto etot metod ne mozhet dat' tochnye rezul'taty i otdal predpochtenie drugomu metodu, na opisanii kotorogo my ostanovimsya pozzhe (sm. § 6.9).

Samo predpolozhenie o nepreryvnosti izmeneniya velichiny <ΔM_V> s izmeneniem δ(0,6) nuzhdaetsya v proverke. Deistvitel'no, vskore posle poyavleniya rassmotrennoi raboty Sendidzha Eggen (1971g; 1973) privel ser'eznye dovody v pol'zu sushestvovaniya pa diagrammah M_bol, lgT_e i M_I, R - I ne polosy, a opyat'-taki posledovatel'nosti subkarlikov. Soglasno Eggenu (1973), dlya zvezd gruppy S v tabl. 6.2 sleduet prinyat' znachenie <ΔM_V> = +0^m,2 ± 0^m,1 pri <δ(0,6)> = +0^m,135 (chemu sootvetstvuet svetlyi kruzhok na ris. 88). V takom sluchae my uzhe ne mozhem pol'zovat'sya krivoi, izobrazhennoi na ris. 88, dlya opredeleniya znachenii <ΔM_V> pri δ(0,6), lezhashih v intervale ot 0^m,05 do 0^m,2. Mozhet byt', krivaya imeet razryv, i pri δ(0,6) ≥ +0^m,16 vse <ΔM_V> = +1^m,2.

K 1979 g. dannye o velichinah zvezd glavnoi posledovatel'nosti v sisteme B, V byli polucheny lish' dlya dvenadcati sharovyh skoplenii: M 2 (Arp, 1959v), M 3 (Dzhonson, Sendidzh, 1956; Sendidzh, 1970), M 5 (Arp, 1962b), M 13 (Sendidzh, 1970), M 15 (Sendidzh, 1970), M 71 (Arp, Hartvik, 1971), M 92 (Sendidzh, 1970), NGC 5053 (Uoker i dr., 1976), NGC 6397 (Vulli i dr., 1961), NGC 6752 (Karni, 1979), 47 Tus (Hesser, Hartvik, 1977) i ω Sen (Kennon, Kontizas, 1974). Daleko ne dlya vseh iz nih imeyutsya nablyudeniya i v sisteme U.

Eto obstoyatel'stvo naryadu s otmechennymi vyshe trudnostyami lokalizacii glavnyh posledovatel'nostei sharovyh skoplenii na diagramme M_V, V - V, do sih por zatrudnyaet tochnoe reshenie problemy opredeleniya rasstoyanii do sharovyh skoplenii. Prezhde chem prodolzhit' opisanie palliativnyh reshenii etoi problemy, neobhodimo rassmotret' osnovnye fizicheskie harakteristiki sharovyh skoplenii i ih chlenov.

<< 6.3 Obshii vid diagramm velichina - pokazatel' cveta zvezd sharovyh skoplenii. Zvezdy glavnoi posledovatel'nosti v etih sistemah i subkarliki | Oglavlenie | 6.5 Spektry yarkih zvezd sharovyh skoplenii. Soderzhanie tyazhelyh elementov v ih atmosferah >>

Publikacii s klyuchevymi slovami: zvezdy - Skoplenie Publikacii so slovami: zvezdy - Skoplenie
Sm. takzhe: Chernaya dyra razrushaet zvezdu: animaciya Zvezdy, pyl' i tumannost' v NGC 6559 25 samyh yarkih zvezd na nochnom nebe Animaciya: chernaya dyra razrushaet zvezdu Kometa, skopleniya i tumannosti Sravnenie razmerov zvezd Samaya dalekaya iz vseh izvestnyh zvezd? Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce