Glava 8. Stroenie i razmery zvezdnyh skoplenii

"I togda ya otkryl svoyu knigu v bol'shom
pereplete,
Gde na pervoi stranice rasteniya viden
chertezh.
I cherna i mertva, protyanulas' ot knigi
k prirode
To li pravda cvetka, to li v nem zaklyuchennaya
lozh'.
I cvetok s udivlen'em smotrel na svoe
otrazhen'e
I kak budto pytalsya chuzhuyu premudrost'
ponyat'."
N. Zabolockii, Vse, chto bylo v dushe...

8.1 Vidimoe raspredelenie zvezd v skopleniyah. Metody analiza otklonenii formy sharovyh skoplenii ot sfericheskoi

Bol'shenstvo sharovyh skoplenii v proekcii na ploskoct', kasatel'nuyu k nebesnoi sfere, imeet ellipticheskuyu formu. Kto oznachaet, chto ih real'naya prostranstvennaya forma otklonyaetsya ot sfericheskoi. Obychno prinimayut, chto sharovye skopleniya yavlyayutsya sferoidami, t. e. splyusnutymi, a ne vytyanutymi, ellipsoidami vrasheniya. V dal'neishem my tozhe budem priderzhivat'sya etoi tochki zreniya. Odnako, poskol'ku sharovye skopleniya dvizhutsya v obshem silovom pole Galaktiki, nel'zya ne schitat'sya s vozmozhnost'yu ih deformacii vneshnimi, naprimer, prilivnymi silami.

Metody analiza otklonenii formy sharovyh skoplenii ot sfericheskoi sovershenstvovalis' postepenno. Pervuyu popytku v etom napravlenii sdelal Beili (1916), podschitavshii dlya 10 skoplenii chisla zvezd v vos'mi 45-gradusnyh sektorah s vershinami v centre skopleniya. Nanesenie etih chisel kak ordinat protiv naimenovanii sootvetstvuyushih sektorov, raspolozhennyh v poryadke vozrastaniya pozicionnyh uglov, davalo predstavlenie o raspredelenii zvezd v dannom skoplenii v zavisimosti ot napravleniya ot ego centra. Etot sposob analiza shiroko ispol'zovalsya zatem Shepli (1930), interpretirovavshim sinusoidal'nuyu volnu na podobnom grafike kak indikator elliptichnosti dannogo skopleniya.

Pozdnee Sheval'e (1918), a takzhe X. Shepli i M. Shepli (1919) vveli v upotreblenie polyarnuyu diagrammu, na kotoroi po radiusam-vektoram otkladyvayutsya otrezki, proporcional'nye chislam zvezd v sootvetstvuyushih sektorah; koncy otrezkov posledovatel'no soedinyayutsya mezhdu soboyu. Dlya issledovaniya elliptichnosti na raznyh rasstoyaniyah ot centra skopleniya rassmatrivalis' chisla zvezd v posledovatel'nyh kol'cevyh zonah razlichnyh sektorov. Opisannye sposoby pozvolyali opredelyat' napravleniya bol'shih osei ellipsov, no ocenka stepeni elliptichnosti ostavalas' v nih chisto kachestvennoi. V toi zhe rabote X. Shepli i M. Shepli (1919), izuchivshie elliptichnost' 41 sharovogo skopleniya, nashli, chto neposredstvennye ocenki vida skoplenii, pa melkomasshtabnyh snimkah, podobnyh kartam Franklin-Adamsa, pozvolyayut naiti napravlenie bol'shoi osi skopleniya tak zhe opredelenno, kak i podschety.

V rabote Shepli i Soier (1927b) stepen' elliptichnosti harakterizuetsya uzhe bolee naglyadno - desyatikratnym otnosheniem maloi osi b ellipsa fotograficheskogo izobrazheniya skopleniya k ego bol'shoi osi a. Etu velichinu avtory nazyvayut elliptichnost'yu, hotya obychno pod elliptichnost'yu ili szhatiem ponimayut velichinu (a - b)/a Shepli i Soier privodyat ocenki elliptichnosti 75 sharovyh skoplenii, no pozicionnye ugly bol'shih osei byli opredeleny imi lish' dlya 37 iz nih.

Froindlih i Heiskanen (1923) predlozhili pervyi analiticheskii metod issledovaniya elliptichnosti sharovyh skoplenii, osnovannyi na opredelenii elementov ellipsa inercii proekcii skopleniya na nebesnuyu sferu. Esli zvezdy skopleniya v proekcii raspredeleny elliptichno, to moment inercii ih sistemy otnositel'no nekotoroi osi, prohodyashei v ploskosti proekcii cherez centr mass sistemy (otozhdestvlyaemyi obychno s centrom skopleniya), kotoryi raven summe kvadratov rasstoyanii chlenov skopleniya ot etoi osi, budet menyat'sya s izmeneniem napravleniya poslednei, dostigaya maksimuma otnositel'no napravleniya maloi osi ellipsa proekcii skopleniya i minimuma - otnositel'no osi, sovpadayushei s bol'shoi os'yu ellipsa proekcii.

Vvodya opredelennye dopusheniya o raspredelenii zvezd, mozhno naiti ne tol'ko napravlenie bol'shoi osi ellipsa raspredeleniya, no i otnoshenie ego osei. Odnako etot sposob analiza malo naglyaden i ne pozvolyaet analizirovat' splyusnutost' ellipsov na raznyh rasstoyaniyah ot centra sistemy. On ne pozvolyaet takzhe vyyavit' asimmetriyu sistemy.

Bruggenkate (1927) v svoei monografii razvil metod dlya tochnogo analiticheskogo opredeleniya elementov ellipsa proekcii skopleniya na nebesnuyu sferu. Skoplenie delitsya na ryad (n) sektorov. V kazhdom sektore stroitsya sootvetstvuyushaya krivaya vidimoi plotnosti F(r), pokazyvayushaya izmenenie etoi plotnosti s izmeneniem rasstoyaniya r ot centra sistemy. Granica skopleniya v dannom napravlenii opredelyaetsya znacheniem r, pri kotorom krivaya F(r) perehodit v plotnost' zvezd fona F₀. Vmesto etoi neuverennoi granicy mozhno opredelyat' krivuyu, sootvetstvuyushuyu nekotoroi postoyannoi vidimoi plotnosti F'₀, slegka prevyshayushei F₀. Eta krivaya prinimaetsya za ellips s centrom, sovpadayushim s centrom skopleniya. Bruggenkate pishet uravnenie ellipsa v pryamougol'nyh koordinatah v vide

$Ax^2 + Bxy + Cy^2 = 1.$ (8.1)

Reshaya po sposobu naimen'shih kvadratov sistemu n takih uravnenii, sostavlennuyu po izvestnym koordinatam n tochek rassmatrivaemogo ellipsa, nahodyat koefficienty A, B i S, po kotorym zatem mozhno naiti poluosi a i b ellipsa, ekscentrisitet ellipsa $e = \sqrt{1 - \left(\frac{b}{a}\right)^2}$ i pozicionnyi ugol φ ego bol'shoi poluosi a.

Bruggenkate primenil etot metod dlya opredeleniya orientacii vneshnih chastei vos'mi skoplenii, dlya kotoryh Piz i Shepli (1917) opublikovali podschety bol'shogo chisla zvezd v nahodyashihsya na raznyh rasstoyaniyah ot centrov skoplenii otrezkah tridcatigradusnyh sektorov.

Togda zhe Kinle (1927), ispol'zovav podschety Piza i Shepli v ih neopublikovannom pervonachal'nom vide (chisla zvezd v kvadratah pryamougol'noi setki, nalozhennoi na negativ), vpervye opublikoval risunki krivyh ravnoi vidimoi plotnosti na raznyh rasstoyaniyah ot centra dlya pyati sharovyh skoplenii. Odnako Kinle ne opredelyal elementy ellipsov, approksimiruyushih eti krivye, a ogranichilsya chisto kachestvennymi zaklyucheniyami, tak kak ego interesovali ne plavnye ellipsoobraznye krivye, a nepravil'nosti na nih, kotorye on interpretiroval kak sledy spiral'noi struktury v skopleniyah ili priznaki istecheniya iz nih zvezd.

Cherez dva goda poyavilas' rabota Hekmana i Zidentopfa (1929), kritikuyushaya vyvody Kinle i ob'yasnyayushaya nepravil'nosti v krivyh postoyannoi vidimoi plotnosti sluchainymi kolebaniyami podschetov. Vopros o priznakah spiral'noi struktury v zvezdnyh skopleniyah, diskutirovavshiisya v 20-h godah (sm., naprimer, Bruggenkate, 1927, s. 63-68), s teh por ser'ezno ne voznikal, hotya otdel'nye issledovateli vremya ot vremeni obrashayut vnimanie na sluchainye konfiguracii zvezd v skopleniyah, napominayushie spirali.

V 1928 g. Shilt (1928) na primere skopleniya ω Cen pokazal vozmozhnost' analiza elliptichnosti sharovyh skoplenii na osnovanii izmerenii raspredeleniya intensivnosti izlucheniya v ih vnefokal'nyh izobrazheniyah. Ekscentrisitety ellipsov ravnoi plotnosti v ω Cen umen'shalis' po mere priblizheniya k centru skopleniya. Densitometricheskie izmereniya diametrov 70 sharovyh skoplenii, kotorye proveli Shepli i Seier (1935), takzhe pokazali zametnye izmeneniya splyusnutosti nekotoryh skoplenii s izmeneniem rasstoyaniya ot ih centra.

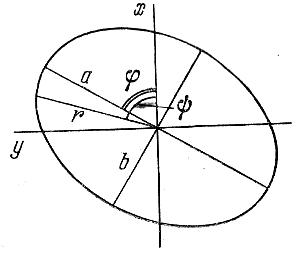
Ris. 115. Shema, poyasnyayushaya vyvod formul (8.2) i (8.3).

V 1952 g. Holopov (1953a) obrabotal vse opublikovannye dannye o podschetah zvezd v dvadcati sharovyh skopleniyah po metodu, blizkomu k metodu Bruggenkate, opredeliv elementy ellipsov ravnoi vidimoi plotnosti zvezd raznyh tipov na raznyh rasstoyaniyah ot centrov rassmotrennyh skoplenii, pol'zuyas' uravneniem ellipsa, zapisannym v polyarnyh koordinatah (ris. 115):

$\frac{1}{r^2} = A + B\sin 2\psi + C\cos 2\psi,$ (8.2)

gde

$A = \frac{1}{2}\left(\frac{1}{a^2} + \frac{1}{b^2}\right), \quad B = \frac{1}{2}\left(\frac{1}{a^2} - \frac{1}{b^2}\right)\sin 2\phi, \quad C = \frac{1}{2}\left(\frac{1}{a^2} - \frac{1}{b^2}\right)\cos 2\phi.$ (8.3)

Opredeliv znacheniya A, V, S putem resheniya po sposobu naimen'shih kvadratov sistemy uslovnyh uravnenii vida (8.2), netrudno otsyuda naiti elementy ellipsa a, b, φ.

V rezul'tate vyyasnilos', chto v sharovyh skopleniyah, kak pravilo, ne sushestvuet edinoi orientacii bol'shih osei krivyh postoyannoi vidimoi plotnosti i edinyh otnoshenii ih poluosei η = b/a dlya podsistem zvezd raznyh tipov i dlya raznyh rasstoyanii r ot centra rassmatrivaemogo skopleniya. Otnoshenie η zaklyucheno v predelah 0,6 ≤ η ≤ 1,0, prichem ono mozhet rasti i ubyvat' s izmeneniem r.

V nekotoryh skopleniyah, kak, naprimer, v M3, M5, M15, nekotorye podsistemy vhodyashih v nih zvezd pokazyvayut povorot bol'shih osei ellipsov ravnoi plotnosti s perehodom k menee plotnym chastyam skoplenii. Etot povorot proishodit, po-vidimomu, ne postepenno, a skoree skachkom, harakterizuya perehod ot odnoi fizicheski odnorodnoi oblasti skopleniya k drugoi. Razlichiya v vidimom raspredelenii zvezdnoi plotnosti, nablyudaemye pri perehode ot bolee plotnyh central'nyh oblastei k menee plotnym vneshnim, ochevidno, sootvetstvuyut analogichnym real'nym razlichiyam v raspredelenii prostranstvennoi plotnosti.

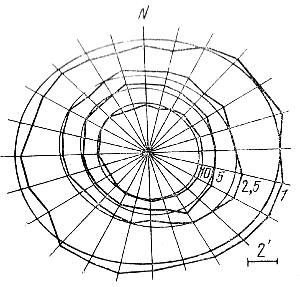
Ris. 116. Krivye ravnoi vidimoi plotnosti zvezd yarche 16^m,8 pv skopleniya M 3. Chisla, stoyashie ryadom s krivymi, sootvetstvuyut chislam zvezd v 1 kv. minute dugi.

Dlya illyustracii skazannogo na ris. 116 privedeny krivye pavnoi vidimoi plotnosti yarkih zvezd skopleniya MZ (vklyuchaya zvezdy vetvi krasnyh gigantov, gorizontal'noi vetvi i verhnei chasti posledovatel'nosti subgigantov).

Otmechennye vyshe u nekotoryh sharovyh skoplenii fakty povorota osei ellipsov ravnoi plotnosti i izmeneniya otnosheniya ih poluosei s rasstoyaniem ot centra shodny s yavleniyami, otmechennymi Ivensom (1951) u nekotoryh ellipticheskih galaktik. Poskol'ku v dinamicheskom otnoshenii sharovye skopleniya i ellipticheskie galaktiki dolzhny byt' ves'ma shodny, to ne udivitel'no, chto oba tipa ob'ektov obnaruzhivayut shodnye yavleniya.

Posle otkrytiya u izobrazhenii ryada sharovyh skoplenii opredelennoi orientacii na nebesnoi sfere razlichnye avtory (X. Shepli, M. Shepli, 1919; Bruggenka-te, 1927; Shepli, Soier, 1927b; Dzhonson, 1952) bezuspeshno pytalis' svyazat' etu orientaciyu s kakoi-libo preimushestvennoi orientaciei osei ili ploskostei simmetrii rassmatrivaemyh sistem v prostranstve i ustanovit' zakonomernosti izmeneniya ih po otnosheniyu k ploskosti ili centru Galaktiki.

Mozhno dumat', chto vsyakie popytki iskat' priznaki preimushestvennoi orientacii sharovyh skoplenii po orientacii ih vnutrennih chastei (a dannye, ispol'zovannye avtorami upomyanutyh vyshe rabot, otnosyatsya imenno k "glavnym telam", ili yadram, skoplenii) obrecheny na neudachu v svyazi s vozmozhnym razlichiem orientacii vnutrennih, promezhutochnyh i vneshnih chastei skoplenii. Skoree mozhno bylo by rasschityvat' zametit' vliyanie vneshnih vozmushenii na vneshnie oblasti podsistem bolee slabyh zvezd sharovyh skoplenii. Odnako nashi dannye svidetel'stvuyut ob otsutstvii rosta elliptichnosti podsistem slabyh zvezd s udaleniem ot centrov skoplenii.

Analiz vidimogo raspredeleniya zvezdnoi plotnosti v rasseyannyh skopleniyah daet menee uverennye rezul'taty v svyazi s men'shim kolichestvom zvezd v etih sistemah i bol'shim vliyaniem zvezd fona na rezul'taty podschetov.

S 1966 g. dlya issledovaniya elliptichnosti sharovyh skoplenii s uspehom primenyaetsya tak nazyvaemyi metod ekvidensit, osnovannyi na ispol'zovanii yavleniya solyarizacii pri nadlezhashei obrabotke fotoemul'sii, pozvolyayushei vydelyat' na izobrazhenii tonkie linii ravnoi plotnosti (Kadla, 1966b; Sistero, Furkad, 1970; Hogner i dr., 1972; Kadla i dr., 1977).

<< 7.4 Prostranstvenno-kinematicheskie harakteristiki zvezdnyh skoplenii i evolyuciya Galaktiki | Oglavlenie | 8.2 Analiticheskie i chislennye metody analiza radial'nogo raspredeleniya prostranstvennoi zvezdnoi plotnosti v skopleniyah >>

Publikacii s klyuchevymi slovami: zvezdy - Skoplenie Publikacii so slovami: zvezdy - Skoplenie
Sm. takzhe: Chernaya dyra razrushaet zvezdu: animaciya Zvezdy, pyl' i tumannost' v NGC 6559 25 samyh yarkih zvezd na nochnom nebe Animaciya: chernaya dyra razrushaet zvezdu Kometa, skopleniya i tumannosti Sravnenie razmerov zvezd Samaya dalekaya iz vseh izvestnyh zvezd? Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce