Astronet > Zvezdnye skopleniya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Zvezdnye skopleniya << 8.1 Vidimoe raspredelenie zvezd v skopleniyah. Metody analiza otklonenii formy sharovyh skoplenii ot sfericheskoi | Oglavlenie | 8.3 Metodika postroeniya krivyh izmeneniya vidimoi plotnosti F(r) >>

8.2 Analiticheskie i chislennye metody analiza radial'nogo raspredeleniya prostranstvennoi zvezdnoi plotnosti v skopleniyah

My znaem, chto, kak pravilo, skopleniya imeyut ellipticheskuyu formu. Prosteishei gipotezoi, kotoruyu my mozhem prinyat' v etom sluchae, budet gipoteza, soglasno kotoroi poverhnosti ravnoi prostranstvennoi plotnosti yavlyayutsya podobnymi i podobno raspolozhennymi sferoidami. V proekcii na ploskost' oni dolzhny predstavlyat'sya podobnymi i podobno raspolozhennymi ellipsami. My znaem, chto v deistvitel'nosti eto ne tak. No otkloneniya ot etoi kartiny obychno maly. Kak pravilo, mozhno prinimat' dlya vsego skopleniya nekotorye srednie parametry elliptichnosti. Estestvenno, chto vnachale zadachu perehoda ot vidimogo raspredeleniya zvezdnoi plotnosti F(r) v skoplenii k raspredeleniyu prostranstvennoi plotnosti f(r) reshali dlya sluchaya sfericheskoi simmetrii raspredeleniya.

a) Analiticheskie metody.

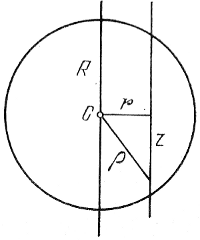
Ris. 117. Shema, poyasnyayushaya vyvod formul (8.4) - (8.6).

Na ris. 117 izobrazhen razrez sfericheskogo skopleniya ploskost'yu, prohodyashei cherez glaz nablyudatelya i centr skopleniya S, R - radius skopleniya. Vidimaya plotnost' zvezd na rasstoyanii r ot centra skopleniya F(r), ochevidno, svyazana s prostranstvennoi zvezdnoi plotnost'yu f(r) sootnosheniem

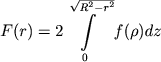
$F(r) = 2 \int\limits_0^{\sqrt{R^2 - r^2}} f(\rho)dz$ (8.4)

ili, tak kak ρ² = r² + z²,

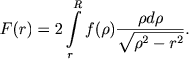
$F(r) = 2 \int\limits_r^R f(\rho)\frac{\rho d\rho}{\sqrt{\rho^2 - r^2}}.$ (8.5)

Vnachale Ceipel' (1908) poluchil i opublikoval ochen' slozhnoe dlya prakticheskogo primeneniya reshenie etogo integral'nogo uravneniya Abelya:

$f(\rho) = \frac{1}{\pi}\int\limits_0^R \sqrt{\rho^2 - r^2} \frac{d}{dr} \left[\frac{F'(r)}{r}\right]dr.$ (8.6)

Vposledstvii Ceipel' i Lindgren (1921) nashli bolee prostoe vyrazhenie dlya opredeleniya f(r):

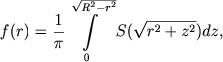
$f(r) = \frac{1}{\pi}\int\limits_0^{\sqrt{R^2 - r^2}} S(\sqrt{r^2 + z^2})dz,$ (8.7)

gde

$S(r) = -\frac{1}{r}\frac{dF(r)}{dr},$ (8.8)

vyvod kotorogo mozhno naiti v lyubom kurse zvezdnoi astronomii (sm., naprimer, Kulikovskii, 1978, s. 141 - 143). Tak kak v (8.7) vhodit proizvodnaya F(r) po r , metod Ceipelya ne trebuet pri ispol'zovanii krivoi F(r) predvaritel'nogo ispravleniya ee za plotnost' zvezd fona, schitayushuyusya obychno postoyannoi.

Ochen' izyashen metod Plammera (1911); po sravneniyu s metodom Ceipelya on isklyuchitel'no prost i poetomu neodnokratno primenyalsya ryadom avtorov. Na ris. 118 hSu - kartinnaya ploskost', prohodyashaya cherez centr skopleniya S . Os' z napravlena k nablyudatelyu. Rassmotrim sechenie skopleniya ploskost'yu y'Oz' , parallel'noi ploskosti yCz i prohodyashei na rasstoyanii OS = r ot ego centra. Oboznachim cherez ρ i l rasstoyaniya lyuboi iz tochek etogo secheniya ot tochek S i O sootvetstvenno.

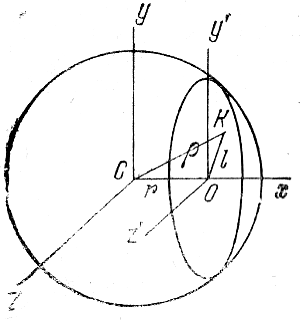
Ris. 118. Shema, poyasnyayushaya vyvod formul (8.9) - (8.13).

Chislo zvezd skopleniya, nablyudaemyh v proekcii na nebesnuyu sferu v polose shirinoi dr , nahodyasheisya na rasstoyanii r ot ego centra, oboznachim cherez F(r)dr . Ochevidno,

$\Phi (r)dr = dr\int\int f(\rho)dydz.$ (8.9)

Perehodya k polyarnym koordinatam v ploskosti y'Oz', mozhem napisat'

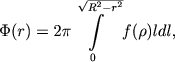
$\Phi (r) = 2\pi \int\limits_0^{\sqrt{R^2 - r^2}} f(\rho)ldl,$ (8.10)

ili, tak kak l² = ρ² - r²,

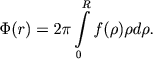
$\Phi (r) = 2\pi \int\limits_0^R f(\rho)\rho d\rho.$ (8.11)

Differenciruya obe chasti ravenstva (8.11) po parametru r , nahodim

$\Phi ' (r) = -2\pi rf(r),$ (8.12)

otkuda

$f(r) = -\frac{\Phi ' (r)}{2\pi r}.$ (8.13)

Pri pol'zovanii etim metodom na praktike proekciya skopleniya razbivaetsya na ryad parallel'nyh polos edinichnoi shiriny, podschety chisel zvezd v kotoryh (za vychetom sootvetstvuyushih chisel zvezd fona) dayut F(r). Udobnuyu dlya nekotoryh prakticheskih celei formulu, osnovannuyu na kombinacii metodov Ceipelya i Plammera, predlozhil Kurt (1969, s. 200):

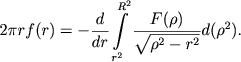
$2\pi rf(r) = -\frac{d}{dr}\int\limits_{r^2}^{R^2} \frac{F(\rho)}{\sqrt{\rho^2 - r^2}}d(\rho^2).$ (8.14)

Obobsheniya metodov Ceipelya i Plammera na sluchai ellipsoidal'nogo raspredeleniya plotnosti byli predlozheny Kinle (1928) i Bruggenkate (1928). K sozhaleniyu, Kinle dal nevernuyu formulu, a Bruggenkate - slishkom chastnoe reshenie, svyazyvayushee raspredelenie prostranstvennoi plotnosti zvezd v skoplenii s raspredeleniem ih vidimoi plotnosti vdol' maloi osi ellipsa proekcii skopleniya.

Obobshenie reshenii Ceipelya i Plammera na sluchai, kogda poverhnosti ravnoi plotnosti v skoplenii yavlyayutsya koncentricheskimi, podobnymi i koaksial'nymi sferoidami, mozhno naiti v rabotah Holopova (1949a, 1953b). Esli η₀ - otnoshenie istinnoi maloi poluosi sferoida (η₀l) k bol'shoi (l), i - naklonenie maloi osi sferoida k luchu zreniya, F(l) - vidimaya plotnost' v tochkah ellipsa s bol'shoi poluos'yu l, a L- bol'shaya poluos' sferoida, ogranichivayushego skoplenie, to prostranstvennaya plotnost' f(l) v tochkah sferoida s bol'shoi poluos'yu l

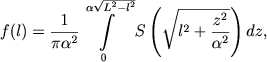
$f(l) = \frac{1}{\pi\alpha^2} \int\limits_0^{\alpha\sqrt{L^2 - l^2}} S\left(\sqrt{l^2 + \frac{z^2}{\alpha^2}}\right)dz,$ (8.15)

gde $S(l) = -\frac{1}{l}\frac{dF(l)}{dl}$ , a $\alpha = \frac{\eta_0}{\sqrt{\eta^2_0\sin^2 i + \cos^2 i}}$ .

Pri η₀ = 1 formula (8.15) perehodit v (8.7). Sootvetstvuyushaya formula, yavlyayushayasya obobsheniem formuly (8.13), imeet vid

$f(l) = -\frac{\Phi '(l)}{2\pi\eta_0 l},$ (8.16)

gde znacheniya F(l) opredelyayutsya podschetami zvezd v polosah, parallel'nyh maloi osi ellipsa proekcii skopleniya na nebesnuyu sferu. Esli ε - nablyudaemyi ekscentrisitet etogo ellipsa, to forma skopleniya opredelyaetsya ekscentrisitetom e ego meridional'nogo secheniya

$e = \frac{\epsilon}{\sin i}.$ (8.17)

Estestvenno, chto pri pol'zovanii formulami (8.15) i (8.16) my mozhem naiti reshenie f(l) tol'ko kak funkciyu i.

Tak kak e ≤ 1, iz (8.17) vytekaet, chto sushestvuet predel'nyi naimen'shii ugol i₀, opredelyaemyi ravenstvom sin i₀ = ε, pri kotorom skoplenie obrashaetsya v disk. Poetomu prakticheski mozhno poluchit' neskol'ko variantov resheniya dlya raznyh znachenii i, lezhashih v predelah ot 90°; do i₀. Real'nyi vybor i ogranichivaetsya tem, chto my ne znaem ni odnogo skopleniya, dlya kotorogo velichina η byla by men'she 0,6, t. e. znachenie e prevyshalo by 0,8.

Dlya prakticheskogo primeneniya analiticheskie metody vse zhe ne ochen' udobny, tak kak trebuyut obrasheniya k trudoemkim operaciyam chislennogo differencirovaniya i integrirovaniya. Poetomu ryad avtorov uzhe davno razrabatyval bolee prostye chislennye metody resheniya zadachi.

b) Chislennye metody. Pervyi iz nih byl razvit Parvulesko (1925), kotoryi prinyal, chto skoplenie sostoit iz n koncentricheskih i vzaimopronikayushih sfer odnorodnoi plotnosti, ubyvayushei po mere rosta radiusa sfery (ris. 119). Eta sistema sfer v proekcii na kartinnuyu ploskost' obrazuet ryad kol'cevyh oblastei, ogranichennyh radiusami $\frac{n}{n}R, \, \frac{n-1}{n}R, \, ..., \, \frac{1}{n}R$ , gde R - radius skopleniya. Na ris. 119 izobrazheny pryamye, po kotorym ploskost' chertezha, prohodyashaya cherez centr skopleniya i glaz nablyudatelya, peresekaetsya kasayushimisya sfer cilindrami, osi kotoryh parallel'ny luchu zreniya.

Dolya chislo zvezd skopleniya, proektiruyushihsya na vneshnyuyu kol'cevuyu oblast', na velichinu sootvetstvuyushego ob'ema, zaklyuchennogo mezhdu poverhnost'yu sfery s radiusom R i poverhnost'yu cilindra, kasatel'nogo k sfere s radiusom $\frac{n-1}{n}R$ , mozhno srazu naiti prostranstvennuyu plotnost' samoi bol'shoi sfery, f(R). Znaya f(R), mozhno opredelit' chislo zvezd etoi sfery, proektiruyushihsya na sleduyushuyu kol'cevuyu oblast', i vychtya ego iz obshego chisla zvezd, nablyudaemyh v etoi oblasti, naiti prihodyashegosya na nee chislo zvezd sfery s radiusom $\frac{n-1}{n}R$ , a zatem i prostranstvennuyu plotnost' zvezd v etoi sfere, $f\left(\frac{n-1}{n}R\right)$ i t.d.

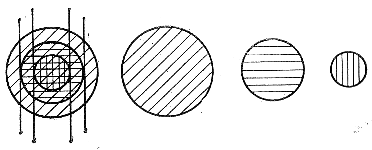
Ris. 119. Shema, poyasnyayushaya ideyu metoda Parvulesko.

Dlya polucheniya znacheniya prostranstvennoi plotnosti na dannom rasstoyanii ot centra skopleniya ostaetsya prosummirovat' plotnosti f vseh sfer, proektiruyushihsya na sootvetstvuyushuyu etomu rasstoyaniyu kol'cevuyu oblast'.

Vtoroi metod, po sushestvu, yavlyayushiisya modifikaciei predydushego, byl nezavisimo predlozhen Vallenkvinstom (1933), kotoryi ispol'zoval vmesto sfer sfericheskie poyasa odinakovoi tolshiny s plotnost'yu, vozrastayushei s priblizheniem k centru, i dal udobnuyu sistemu formul dlya posledovatel'nogo opredeleniya f(r) v desyati sfericheskih poyasah, na kotorye razbivalos' skoplenie, nachinaya s naruzhnogo poyasa i konchaya central'noi sferoi.

Pozzhe Vallenkvist (1960) opublikoval analogichnyi metod, v kotorom predusmotreno uvelichenie shiriny poyasov, na kotorye razbivaetsya skoplenie, s uvelicheniem rasstoyaniya ot centra, chto racional'no, tak kak vo vneshnih oblastyah plotnost' menyaetsya medlennee, chem v centre. V toi zhe rabote, po-vidimomu, dlya polnoty razrabotki problemy Vallenkvist predlozhil chislennyi metod, osnovannyi na provedenii podschetov zvezd ne v kol'cah, a v parallel'nyh polosah, - analog analiticheskogo metoda Plammera. Razob'em proekciyu skopleniya na n kolec odinakovoi shiriny i n parallel'nyh polos, granicy kotoryh - kasatel'nye k sootvetstvuyushim okruzhnostyam. Vvedem oboznacheniya: r_n - radius skopleniya, r_m - radius m-go kol'ca (m < n), N_m - chislo zvezd, nablyudaemyh v m-i polose (posle ucheta fona), a f_m - srednyaya prostranstvennaya plotnost' v predelah m-go sfericheskogo poyasa (ogranichennogo radiusami r_m i r_m-1). Togda

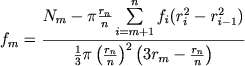
$f_m = \frac{N_m - \pi\frac{r_n}{n}\sum\limits_{i=m+1}^{n} f_i(r_i^2 - r_{i-1}^2)}{\frac{1}{3}\pi\left(\frac{r_n}{n}\right)^2\left(3r_m - \frac{r_n}{n}\right)}$ (8.18)

V 1965 g. Kuzmin i Veltmann (1972) primenili metodiku Plammera dlya nahozhdeniya raspredeleniya prostranstvennoi plotnosti zvezd v sharovyh skopleniyah M 3 i M 15 putem fotoelektricheskih nablyudenii, skaniruya skoplenie dlinnoi uzkoi shel'yu (13",4 x 447") v napravlenii, perpendikulyarnom k dline sheli. Prostoe differencirovanie potoka izlucheniya, postupayushego ot sheli, pozvolyaet poluchit', v sootvetstvii s formuloi (8.13), raspredelenie prostranstvennoi plotnosti zvezd v skoplenii (sm. takzhe Kuzmin i dr., 1977).

Obobshenie pervogo chislennogo metoda Vallenkvista (1933) na sluchai, kogda skoplenie yavlyaetsya sferoidom, prichem poverhnosti ravnoi plotnosti v nem sut' koncentricheskie, podobnye i podobno raspolozhennye sferoidy, bylo predlozheno Holopovym (1949b), opublikovavshim sistemu formul dlya posledovatel'nogo vychisleniya znachenii prostranstvennoi plotnosti f_i v 25 sferoidal'nyh poyasah, na kotorye delitsya skoplenie, po znacheniyam srednei vidimoi plotnosti F_i, opredelyaemym v sootvetstvuyushih ellipticheskih kol'cah, ogranichennyh ellipsami postoyannoi vidimoi plotnosti.

Esli oboznachit' cherez a_m bol'shuyu poluos' m-go sferoida (schitaya, chto a_m-1 < a_m), to

$\begin{array}{ll} f_m &=\frac{3}{4}aF_m(a_m^2 - a_{m-1}^2)^{-1/2} - (a_m^2 - a_{m-1}^2)^{-3/2} \times \\ &\times\sum\limits_{i=m+1}^{n} f_i \Bigl((a_i^2 - a_{m-1}^2)^{3/2} - (a_i^2 - a_m^2)^{3/2} - \\ &-[(a_{i-1}^2 - a_{m-1}^2)^{3/2} - (a_{i-1}^2 - a_m^2)^{3/2}]\Bigl) \end{array}$ (8.19)

gde

$a = \eta \sin i(\eta^2 - \cos^2 i)^{-1/2} = \eta_0^{-1}(\eta_0^{2} \sin^2 i + \cos^2 i)^{1/2},$ (8.20)

i - ugol mezhdu os'yu vrasheniya skopleniya i luchom zreniya, η - otnoshenie vidimoi maloi osi ellipsa proekcii skopleniya k bol'shoi, η₀ - otnoshenie istinnoi maloi osi skopleniya k bol'shoi. Sistema formul (8.19), gde n = 1, 2, ..., n, otlichaetsya ot sistemy formul Vallenkvista (1933) lish' nalichiem mnozhitelya a v pervom chlene kazhdoi formuly.

Pri vychislenii Koefficientov sistemy (8.19) udobnee vsegoprinyat' za edinicu dliny 1/n bol'shoi poluosi vneshnego sferoida, vyrazhaya v etih edinicah F_m i f_m i schitaya, chto a₁ = 1, a₂ = 2, ..., a_n = n. Chem bol'she n, tem tochnee budut poluchaemye znacheniya f_m. Vallenkvist (1933) vychislil znacheniya koefficientov svoei sistemy pri n = 10, Holopov (1949b) - pri n = 25. V poslednem sluchae sistema formul (8.19) imeet vid

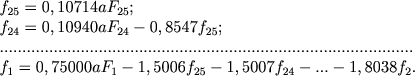
$\begin{array}{l} f_{25} = 0,10714aF_{25}; \\ f_{24} = 0,10940aF_{24} - 0,8547f_{25}; \\ ............................................................................................\\ f_{1} = 0,75000aF_{1} - 1,5006f_{25} - 1,5007f_{24} - ... - 1,8038f_{2}. \end{array}$ (8.21)

My ne privodim ee polnost'yu, tak kak pri ispol'zovanii EVM proshe predostavit' samoi mashine vychislenie koefficientov po formule (8.19), chem vvodit' v ee pamyat' massiv, soderzhashii 325 izvestnyh chisel.

Pri η = 1 i n = 10 iz formul (8.21), kak chastnyi sluchai, poluchayutsya formuly Vallenkvista (1933) putem prostogo otbrasyvaniya lishnih slagaemyh s indeksami, bol'shimi 10. Voobshe, kak vidno iz (8.19), mozhno razbit' skoplenie na lyuboe chislo poyasov l ≤ n i pol'zovat'sya poluchennymi formulami (8.19) ili (8.21), otbrosiv vse chleny s indeksami, ból'shimi l, t. e. prosto schitaya, chto pri i > 1 vse f_i = 0.

Sistema (8.21) pokazyvaet takzhe, chto dlya ee resheniya pri a ≠ 1 mozhno snachala reshit' ee pri uslovii, chto a = 1, a zatem lish' umnozhit' vse poluchennye znacheniya f_m na a. Takim obrazom, forma krivoi f(l) ne zavisit ot velichiny neizvestnogo nam ugla i mezhdu os'yu simmetrii sistemy i luchom zreniya: umnozhenie vseh znachenii f_m na a svoditsya k izmeneniyu chisla zvezd v rassmatrivaemoi gruppe, chto ekvivalentno rastyazheniyu ili szhatiyu krivoi f(l) po osi ordinat bez izmeneniya ee formy.

Krome togo, netrudno videt', chto sistema (8.21) primenima i dlya sluchaya, kogda skoplenie yavlyaetsya vytyanutym ellipsoidom vrasheniya (Holopov, 1953v). Edinstvennaya raznica pri obrabotke sostoit v tom, chto za ekvatorial'nuyu poluos' pri etom prinimaetsya malaya poluos' ellipsa proekcii skopleniya, a η okazyvaetsya bol'she 1. Takim obrazom, forma krivoi f(l) ne zavisit i ot togo, yavlyaetsya li ellipsoid vrasheniya v deistvitel'nosti splyusnutym ili vytyanutym. Osobennosti funkcii raspredeleniya prostranstvennoi plotnosti zvezd v skoplenii f(l) v rassmotrennom priblizhenii opredelyayutsya lish' osobennostyami funkcii raspredeleniya ih vidimoi plotnosti F(l).

Sistema (8.21) chrezvychaino udobna i v tom otnoshenii, chto s ee pomosh'yu mozhno, znaya raspredelenie f(l) vo vneshnih oblastyah skopleniya, uchityvat' vliyanie etih oblastei na raspredelenie F(l) vo vnutrennih oblastyah. Dlya etogo dostatochno vo vseh formulah, soderzhashih, naprimer, F_i s i ≤ m, priravnyat' nulyu znacheniya f_i s i ≤ m i vychislit' zatem sootvetstvuyushie znacheniya F_i po izvestnym dlya i > m znacheniyam f_i.

Dlya tochnogo vychisleniya f(r) vo vneshnih oblastyah skoplenii bol'shih uglovyh razmerov (R > 5°;), kakim yavlyayutsya, naprimer, Giady, uzhe nel'zya prenebregat' neparallel'nost'yu pryamyh, soedinyayushih glaz nablyudatelya s granicami poverhnostei ravnoi plotnosti v etih sistemah. V etom sluchae upomyanutye pryamye yavlyayutsya obrazuyushimi uzhe ne cilindricheskih, a konicheskih poverhnostei. Sootvetstvuyushie sistemy formul chislennogo metoda dlya opredeleniya prostranstvennoi plotnosti v sfericheskih sistemah, uglovye radiusy kotoryh dostigayut 15, 30, 60 i 90 gradusov, po raspredeleniyu vidimoi plotnosti ih chlenov opublikoval Nalimov (1967).

Metod resheniya uravneniya (8.5), pozvolyayushii sudit' o tochnosti opredeleniya funkcii f(r), predlozhil Kosarev (1973).

<< 8.1 Vidimoe raspredelenie zvezd v skopleniyah. Metody analiza otklonenii formy sharovyh skoplenii ot sfericheskoi | Oglavlenie | 8.3 Metodika postroeniya krivyh izmeneniya vidimoi plotnosti F(r) >>

Publikacii s klyuchevymi slovami: zvezdy - Skoplenie Publikacii so slovami: zvezdy - Skoplenie
Sm. takzhe: Chernaya dyra razrushaet zvezdu: animaciya Zvezdy, pyl' i tumannost' v NGC 6559 25 samyh yarkih zvezd na nochnom nebe Animaciya: chernaya dyra razrushaet zvezdu Kometa, skopleniya i tumannosti Sravnenie razmerov zvezd Samaya dalekaya iz vseh izvestnyh zvezd? Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce