Astronet > Zvezdnye skopleniya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Zvezdnye skopleniya << 8.2 Analiticheskie i chislennye metody analiza radial'nogo raspredeleniya prostranstvennoi zvezdnoi plotnosti v skopleniyah | Oglavlenie | 8.4 Yadra i korony - osnovnye oblasti zvezdnyh skoplenii >>

8.3 Metodika postroeniya krivyh izmeneniya vidimoi plotnosti F(r)

Obychno krivuyu izmeneniya vidimoi plotnosti F(r) ctroyat sleduyushim obrazom. Proekciya skopleniya (dlya prostoty budem schitat' ego sfericheskim) delitsya koncentricheskimi okruzhnostyami na neskol'ko kol'cevyh poyasov, shirina kotoryh vybiraetsya v zavisimosti ot chisla rassmatrivaemyh v skoplenii zvezd. Chislo zvezd n v kazhdom kol'ce delitsya na ploshad' poslednego s. Rezul'taty deleniya otkladyvayutsya na grafike po osi ordinat, prichem za abscissy nanosimyh tochek prinimayutsya radiusy okruzhnostei $\bar r$ , delyashih sootvetstvuyushie kol'cevye poyasa ni ravnye po ploshadi chasti. Cherech nemnogochislennye poluchennye tochki provoditsya ot ruki sglazhennaya krivaya, prinimaemaya za krivuyu F(r). Poskol'ku estestvennye fluktuacii chisel p pri sluchainom raspredelenii zvezd v predelah kazhdogo kol'ca sostavlyayut ± $\sqrt n$ , fluktuacii Δ F plotnosti F(r) v kazhdoi tochke dostigayut ± $\frac{\sqrt n}{s}$ , t. e.

$\Delta F = \pm \frac{F(r)}{\sqrt n},$ (8.22)

gde n - chislo zvezd, ispol'zovannoe dlya opredeleniya dannogo znacheniya srednei plotnosti F(r).

Pri takom sposobe postroeniya krivoi F(r) polozheniya tochek, a sledovatel'no, i forma provodimoi po nim krivoi, zavisyat ot shiriny i granic izbrannyh kol'cevyh zon. Chtoby izbezhat' etoi zavisimosti i poluchit' bolee ob'ektivnuyu krivuyu F(r), sleduet proizvodit' podschety zvezd v zonah razlichnoi shiriny Δ, nanosya na odin grafik vse poluchaemye tochki raznymi znachkami k zavisimosti ot shiriny zony. Krome togo, mozhno uvelichit' chislo tochek, posledovatel'no smeshaya po r granicy kol'cevyh zon.

Takim obrazom, dlya kazhdoi vybrannoi shiriny kol'cevyh zon poluchali celaya seriya zon, perekryvayushihsya tak, chtoby sootvetstvuyushie im tochki, po vozmozhnosti ravnomerno raspredelyayas' vdol' krivoi F(r), fakticheski obrisovyvali ee.

Cherez poluchennuyu sovokupnost' tochek provoditsya po vozmozhnosti blizkaya k etim tochkam plavnaya krivaya. Pri etom, kogda s udaleniem ot centra skopleniya vozrastaet rasseyanie tochek, sootvetstvuyushih menee shirokim zonam, hod krivoi opredelyaetsya tochkami, poluchennymi s bolee shirokimi zonami. Eto pozvolyaet umen'shit' vliyanie fluktuacii.

Dlya illyustracii na ris. 120 (Holopov, 1953v) pokazana krivaya raspredeleniya vidimoi (F) plotnosti 136 peremennyh zvezd tipa RR Liry v skoplenii ω Sen, postroennaya takim obrazom v predpolozhenii, chto ih raspredelenie yavlyaetsya sfericheskim. Na tom zhe risunke pokazana krivaya raspredeleniya prostranstvennoi plotnosti (f) etih peremennyh, poluchennaya iz krivoi F analiticheskim ceipelevskim (kruzhki s tochkami) i nashim chislennym (krestiki) metodami. Radius skopleniya prinyat ravnym 25', edinica dliny ravna 1'. Soglasie rezul'tatov, poluchennyh oboimi metodami, prevoshodno.

Esli by krivaya F(r) ne byla "materializovana" bol'shim chislom tochek, a ee prishlos' by provodit', kak eto delayut mnogie, vsego lish' cherez neskol'ko tochek, takie detali krivoi f(r), kak rezkoe izmenenie gradienta plotnosti v raionah r ≈ 6 i 16,5 byli by poteryany. Dazhe cherez tochki F(r), izobrazhennye na ris. 120, my uvereny, bol'shinstvo issledovatelei proveli by plavnuyu krivuyu, ne poveriv v real'nost' volnoobraznyh izmenenii plotnosti v raione 14 < r < 25.

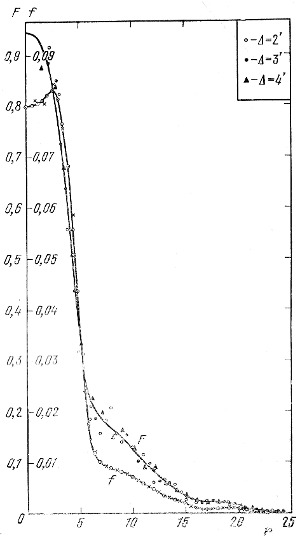
Ris. 120. Krivye vidimogo (F) i prostranstvennogo (f) raspredeleniya peremennyh tipa RR Liry v skoplenii ω Sen (Δ - shirina kol'cevoi zony). Krivaya F preobrazovana v krivuyu f metodom Ceipelya i tochnym chislennym metodom.

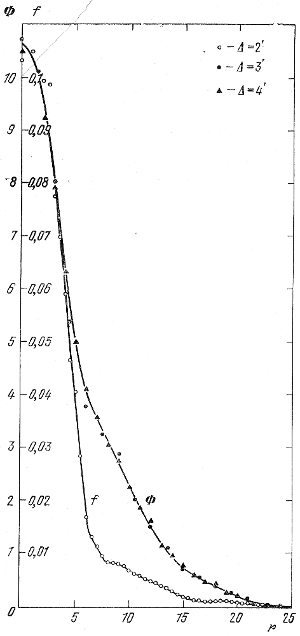
Ris. 121. Krivye F(r) i f(r) raspredeleniya peremennyh tipa RR Liry v skoplenii ω Sen (Δ - shirina polosy), poluchennye po metodu Plammera.

Dlya kontrolya pravil'nosti nashei interpretacii nablyudaemogo hoda krivoi F(r) my poluchili tu zhe krivuyu f(r) metodom Plammera. Kazhdaya seriya perekryvayushihsya polos dannoi shiriny posledovatel'no povorachivalas' cherez kazhdye 15°; na 180°; . Rezul'taty posledovatel'nyh podschetov sootvetstvuyushim obrazom usrednyalis'. Poluchennye takim obrazom krivye F(r) i f(r) izobrazheny na ris. 121 ( Δ - shirina polosy). My vidim, chto pri sovershenno raznom haraktere krivyh F i F na ris. 120 i 121, pri sovershenno raznyh metodah analiza, poluchennye krivye f(r) v raione 9 < r < 25 na etih risunkah prekrasno soglasuyutsya mezhdu soboi, chego ne bylo by, esli by krivaya F(r) na ris. 120 byla provedena inache. Lish' v raione 6-8' ot centra i v samom centre nablyudayutsya zametnye rashozhdeniya. Pochemu?

Central'nye plotnosti bolee nadezhno opredelyayutsya po metodu Plammera, ibo v dannom sluchae v ih opredelenii uchastvuet naibol'shee chislo zvezd n, a oshibki krivyh F(r)) v central'nyh oblastyah maksimal'ny, ibo s umen'sheniem r umen'shayutsya s i n i vozrastayut znacheniya Δ F, opredelyaemye sootnosheniem (8.22).

Chto zhe kasaetsya rashozhdenii v raione 6 < r < 8, to obratim vnimanie na to, chto v etom raione proishodit ochen' bystroe izmenenie gradientov kak funkcii F(r), tak i funkcii F(r). Imenno v etom sluchae vystupaet na scenu dopuskaemaya pochti vsemi issledovatelyami pri postroenii krivyh F(r)) i F(r)) oshibka, uslovno nazvannaya nami oshibkoi intervala. Eta oshibka svyazana s nevernym naneseniem na grafik znachenii F i F, poluchaemyh iz podschetov zvezd v kol'cah i polosah dannoi shiriny Δ.

Kak uzhe otmechalos', obychno znacheniya F(r), vychislyaemye dlya dannoi kol'cevoi zony, otnosyat k rasstoyaniyu r, ravnomu kvadratnomu kornyu iz polusummy kvadratov radiusov okruzhnostei, ogranichivayushih zonu. V deistvitel'nosti zhe ih nuzhno otnosit' k rasstoyaniyam r_c, poluchaemym iz sootnosheniya

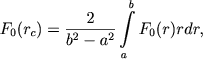
$F_0(r_c) = \frac{2}{b^2 - a^2}\int\limits_a^b F_0(r)rdr,$ (8.23)

gde a i b - sootvetstvenno radiusy vnutrennei i vneshnei okruzhnostei, ogranichivayushih zonu, a F₀(r) - istinnaya krivaya raspredeleniya vidimoi plotnosti, pervym priblizheniem k kotoroi yavlyaetsya postroennaya na ris. 120 krivaya F(r).

Raznost' $\bar r$ - r_c i predstavlyaet soboi oshibku intervala. Ona tem bol'she, chem bol'she shirina kol'cevoi zony Δ = b - a, i dostigaet osobenno bol'shih znachenii, kogda $\frac{dF}{dr}$ v predelah zony preterpevaet bystroe monotonnoe izmenenie.

Dlya ucheta oshibki intervala nuzhno opredelit' znacheniya r_c dlya vseh kol'cevyh zon, ispol'zuemyh pri postroenii krivoi F(r). Pervym priblizheniem k krivoi F₀(r) yavlyaetsya krivaya F( $\bar r$ ), postroennaya pri prinyatii za abscissy nanosimyh tochek znachenii $\bar r$ . S etoi krivoi cherez ravnye promezhutki r, dostatochno malye dlya vypolneniya operacii chislennogo integrirovaniya, snimaetsya ryad posledovatel'nyh znachenii F(r), ohvatyvayushii pochti vsyu krivuyu. Zatem dlya ryada ispol'zovannyh kol'cevyh zon dannoi shiriny, ravnomerno raspredelennyh po oblasti skopleniya, vychislyayutsya po formule (8.23), gde vmesto F₀(r) beretsya F( $\bar r$ ), znacheniya srednih plotnostei, po kotorym s krivoi F( $\bar r$ ) snimayutsya znacheniya r_c pervogo priblizheniya. Raznosti r_c - $\bar r$ otkladyvayutsya na grafike protiv sootvetstvuyushih znachenii $\bar r$ . Cherez poluchennye tochki provoditsya plavnaya krivaya. Podobnye krivye stroyatsya dlya vseh Δ i ispol'zuyutsya dlya perehoda ot absciss $\bar r$ k abscissam r_c.

S poluchennymi znacheniyami r_c stroitsya vtoroe priblizhenie krivoi vidimoi plotnosti, kotoroe mozhno prinyat' za okonchatel'noe, F₀(r_c), ibo pri povtorenii operacii znacheniya gs prakticheski ne menyayutsya. Uchet oshibki intervala svodit vmeste tochki, poluchennye po kol'cevym zonam raznoi shiriny i, chto samoe glavnoe, pozvolyaet obnaruzhit' real'nyi hod krivoi F(r) v oblasti bystrogo izmeneniya $\frac{dF}{dr}$ .

V sluchae ellipticheskih kol'cevyh zon vmesto radiusov berutsya bol'shie poluosi ellipsov $\bar l$ , l_c. Na ris. 122, a my privodim krivuyu F( $\bar l$ ) dlya sistemy peremennyh tipa RR Liry v ω Sen, sootvetstvuyushuyu nablyudaemym parametram elliptichnosti etoi sistemy (η = 0,75, φ = 90°;). Na ris. 122, v pokazany krivye, poluchennye dlya ucheta oshibki intervala, a na ris. 122, b - okonchatel'naya krivaya F(l_c), i sootvetstvuyushaya ei krivaya f(l_c), naidennaya po formulam (8.21) pri uslovii, chto a = 1 (i = 90°;).

Sravnenie ris. 120 i 122 pokazyvaet, chto, ne znaya parametrov elliptichnosti izuchaemoi sistemy, nel'zya poruchit'sya za pravil'nost' detalei poluchaemoi krivoi raspredeleniya prostranstvennoi zvezdnoi plotnosti v sisteme.

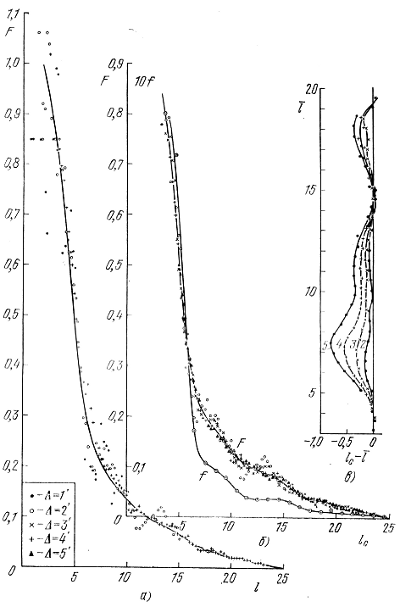
Ris. 122. (a) - predvaritel'naya krivaya F(l), (b) - okonchatel'naya krivaya F(l_c) i krivaya f(l_c) raspredeleniya plotnosti peremennyh tipa RR Liry v skoplenii ω Sen (pri parametrah elliptichnosti η = 0,75, φ = 90°;), (v) - krivye dlya ucheta oshibki intervala.

<< 8.2 Analiticheskie i chislennye metody analiza radial'nogo raspredeleniya prostranstvennoi zvezdnoi plotnosti v skopleniyah | Oglavlenie | 8.4 Yadra i korony - osnovnye oblasti zvezdnyh skoplenii >>

Publikacii s klyuchevymi slovami: zvezdy - Skoplenie Publikacii so slovami: zvezdy - Skoplenie
Sm. takzhe: Chernaya dyra razrushaet zvezdu: animaciya Zvezdy, pyl' i tumannost' v NGC 6559 25 samyh yarkih zvezd na nochnom nebe Animaciya: chernaya dyra razrushaet zvezdu Kometa, skopleniya i tumannosti Sravnenie razmerov zvezd Samaya dalekaya iz vseh izvestnyh zvezd? Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce