Astronet > Zvezdnye skopleniya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Zvezdnye skopleniya << 8.4 Yadra i korony - osnovnye oblasti zvezdnyh skoplenii | Oglavlenie | 8.6 Edinstvo stroeniya zvezdnyh skoplenii. Logarifmicheskii diapazon plotnostei >>

8.5 Predel'nyi radius zvezdnyh skoplenii i ustoichivost' ih koronal'nyh oblastei v pole prilivnyh sil Galaktiki

Skopleniya dvizhutsya v obshem silovom pole Galaktiki. Tak kak plotnost' v nih padaet s udaleniem ot centra, to pri etom nepreryvno umen'shaetsya i sila prityazheniya skopleniem zvezd, kotorye yavlyayutsya ego chlenami. Na nekotorom rasstoyanii ot centra skopleniya sila prityazheniya zvezdy skopleniem uravnoveshivaetsya raznost'yu vneshnih sil prityazheniya, deistvuyushih na zvezdu i centr mass skopleniya so storony galakticheskogo centra. Nachinaya s etogo rasstoyaniya zvezdy budut dvigat'sya uzhe pod deistviem vneshnih sil, t. e. poteryayut svyaz' so skopleniem. Eto rasstoyanie mozhno nazvat' radiusom ustoichivosti skopleniya po otnosheniyu k prilivnym silam Galaktiki, ili predel'nym radiusom skopleniya.

Pust' skoplenie s massoi $\mathfrak{M_c}$ padaet po pryamoi na centr Galaktiki, gde sosredotochena vsya ee massa $\mathfrak{M_g}$ . Rasstoyanie mezhdu nimi oboznachim cherez R_g. Pust' nekotoraya zvezda skopleniya nahoditsya na rasstoyanii r ot ego centra na linii, soedinyayushei centr skopleniya s centrom Galaktiki, blizhe k poslednemu. Uskorenie b_g, ispytyvaemoe zvezdoi v silovom pole Galaktiki po napravleniyu k centru Galaktiki otnositel'no skopleniya, opredelyaetsya ravenstvom

$b_g = \frac{G\mathfrak{M_g}}{(R_g - r)^2} - \frac{G\mathfrak{M_g}}{R_g^2},$ (8.24)

gde G - postoyannaya tyagoteniya, ili, tak kak R_g 》 r,

$b_g = \frac{2Gr\mathfrak{M_g}}{R_g^3},$ (8.25)

Uskorenie b_c, ispytyvaemoe zvezdoi po napravleniyu k centru skopleniya v silovom pole poslednego, est'

$b_c = \frac{G\mathfrak{M_c}}{r^2}.$ (8.26)

Zvezda pokidaet skoplenie, esli b_g > b_c. Predel'nyi radius skopleniya r_s, opredelyaetsya iz usloviya

$b_g(r_s) = b_c(r_s),$ (8.27)

otkuda

$r_s = R_g \sqrt[3]{\frac{\mathfrak{M_c}}{2\mathfrak{M_g}}}.$ (8.28)

Eta formula vpervye byla poluchena i opublikovana Hernerom (1957). Dlya skopleniya, dvizhushegosya po ellipticheskoi orbite s e = 0,5, znachenie predel'nogo radiusa, soglasno Kingu (1962), opredelyaetsya po formule

$r_s = R_p \sqrt[3]{\frac{\mathfrak{M_c}}{3,5\mathfrak{M_g}}},$ (8.29)

gde R_p - perigalakticheskoe rasstoyanie skopleniya.

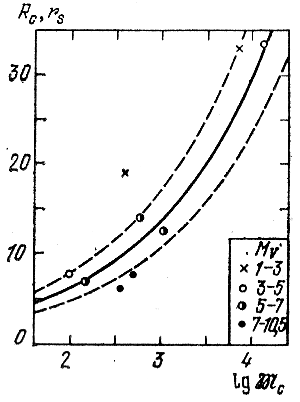
Ris. 127. Zavisimost' predel'nyh radiusov r_s skoplenii, nahodyashihsya v okrestnostyah Solnca, ot logarifmov mass etih sistem (sploshnaya liniya). R_c - nablyudaemye radiusy skoplenii.

Dlya dannogo sharovogo skopleniya velichina R_p mozhet byt' neizvestna, po my znaem ee verhnii predel, t. e. nyneshnee rasstoyanie skopleniya ot centra Galaktiki. Formula (8.29) pokazyvaet, chto nablyudaemye razmery skoplenii, dvizhushihsya po vytyanutym orbitam, mogut byt' sushestvenno men'she predel'nyh razmerov, sootvetstvuyushih ih nyneshnemu rasstoyaniyu ot galakticheskogo centra, hotya by potomu, chto pri periodicheskom prohozhdenii cherez perigalaktii vneshnie razrezhennye sloi skopleniya budut sistematicheski sryvat'sya s nego vozrastayushimi prilivnymi silami.

Po ocenkam Kinga (1962), nablyudaemye radiusy sharovyh skoplenii M 13 i M 15 v 1,5-2 raza men'she ih vozmozhnyh predel'nyh radiusov. Rassmotrim vopros o dinamicheskoi ustoichivosti koronal'nyh oblastei rasseyannyh zvezdnyh skoplenii v pole prilivnyh sil Galaktiki.

Sistema, dvizhushayasya po krugovoi orbite na rasstoyanii Solnca ot centra Galaktiki, mozhet schitat'sya ustoichivoi, esli ee srednyaya plotnost' prevyshaet kriticheskoe znachenie, kotoroe na etom rasstoyanii dlya sfericheskih skoplenii ravno 0, 15 mass Solnca/ps³, a dlya sferoidal'nyh s predel'no malym otnosheniem poluosei 0,6 sostavlyaet 0,19 mass Solnca/ps³ (sm. § 4.4). Proizvodivshiesya do sih por ocenki srednei plotnosti yader rasseyannyh skoplenii vsegda privodili k znacheniyam, znachitel'no prevyshayushim kriticheskoe.

S uvelicheniem istinnogo ob'ema rasseyannyh skoplenii (t. e. s neobhodimost'yu ucheta ih koronal'nyh oblastei) srednyaya plotnost' etih ob'ektov sushestvenno ponizhaetsya. No i v etom sluchae sistemy prodolzhayut ostavat'sya ustoichivymi v pole prilivnyh sil Galaktiki.

V samom dele, esli prinimat' za radiusy skoplenii radiusy ih koronal'nyh oblastei, to srednyaya plotnost' skoplenii Pleyady i Yasli (edinstvennyh naibolee horosho izuchennyh v interesuyushem nas aspekte) ravna sootvetstvenno 0,18 i 0,25 massy Solnca/ps³, t. e., nesomnenno, prevyshaet kriticheskuyu.

Dlya ocenki stepeni ustoichivosti koron skoplenii mozhno vospol'zovat'sya takzhe formuloi (8.29). Prinyav v dannom sluchae, chto R_p = 10 kps, $\mathfrak{M_g}$ = 2 · 10¹¹ mass Solnca, mozhno vychislit' po nei znacheniya predel'nyh radiusov skoplenii, nahodyashihsya v okrestnostyah Solnca, v zavisimosti ot logarifmov mass etih skoplenii. Eta zavisimost' izobrazhena na ris. 127 sploshnoi liniei. Preryvistye krivye sootvetstvuyut analogichnym zavisimostyam, postroennym v predpolozhenii, chto massa Galaktiki vdvoe prevyshaet prinyatoe znachenie (nizhnyaya krivaya) ili vdvoe men'she poslednego (verhnyaya krivaya).

Dlya sravneniya etoi zavisimosti s nablyudeniyami obratimsya k tabl. 8.1, v kotoroi privedeny nekotorye harakteristiki pochti vseh skoplenii, izuchennyh po metodike, opisannoi v dvuh predydushih paragrafah.

Tablica 8.1

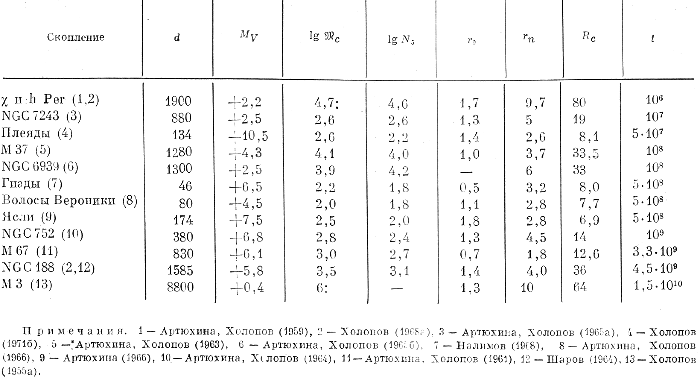
V pervom stolbce tablicy ukazano nazvanie skopleniya, soprovozhdaemoe (v skobkah) nomerom primechaniya k tablice, soderzhashego ssylku na rabotu, posvyashennuyu issledovaniyu dannogo skopleniya. Vo vtorom stolbce - vyrazhennoe v parsekah rasstoyanie do skopleniya, prinyatoe dlya vychisleniya ego razmerov. Tretii stolbec soderzhit predel'nuyu absolyutnuyu velichinu M_V zvezd skopleniya, izuchennyh avtorom raboty, ukazannoi v primechaniyah, chetvertyi - znachenie nizhnego predela logarifma massy skopleniya (vyrazhennoi v edinicah massy Solnca), sootvetstvuyushego velichine M_V. V pyatom stolbce daetsya logarifm chisla zvezd skopleniya yarche pyatoi absolyutnoi vizual'noi velichiny. V ryade sluchaev znacheniya N₅ polucheny putem ekstrapolyacii izvestnogo uchastka funkcii svetimosti skopleniya. V shestom, sed'mom i vos'mom stolbcah privodyatsya vyrazhennye v parsekah znacheniya radiusov central'noi zony yadra (r₀), yadra (r_n) i korony (R_c) skopleniya. V poslednem stolbce priveden vyrazhennyi v godah priblizitel'nyi vozrast skopleniya t, opredelennyi po polozheniyu tochki povorota glavnoi posledovatel'nosti. Znacheniya t dlya M 67 i NGC 188 dany po rabote Tvaroga (1978).

Znacheniya radiusov skoplenii R_c kak funkcii logarifmov sootvetstvuyushih mass $\mathfrak{M_g}$ , vzyatye iz tabl. 8.1, naneseny na ris. 127 razlichnymi simvolami, zavisyashimi ot velichiny M_V, poyasnennymi na risunke.

Ris. 127 svidetel'stvuet o dinamicheskoi ustoichivosti koronal'nyh oblastei rassmotrennyh skoplenii. V samom delo, raspolozhenie tochek na ris. 127 sleduet forme krivoi predel'nyh radiusov. Chem slabee predel'naya absolyutnaya velichina ohvachennyh podschetami zvezd skoplenii, tem blizhe k krivoi predel'nyh radiusov raspolagayutsya sootvetstvuyushie tochki. Nablyudaemye radiusy koron skoplenii Pleyady i Yasli opredelenno men'she vozmozhnogo predel'nogo radiusa skopleniya sootvetstvuyushei massy. Poskol'ku radius korony skopleniya ne vozrastaet sushestvenno s umen'sheniem svetimosti ego chlenov (kak pokazano nami na primere ryada bogatyh skoplenii, v tom chisle i sharovyh), s vyyavleniem vse bolee slabyh chlenov (rostom M_V) tochki na ris. 127 budut. smeshat'sya pri etom vpravo, i podobno tochkam, sootvetstvuyushim skopleniyam Pleyady i Yasli, mogut okazat'sya pod krivoi predel'nyh radiusov.

Takim obrazom, mozhno schitat', chto koronal'nye oblasti skoplenii dinamicheski ustoichivy v pole prilivnyh sil Galaktiki. Oni obrazovany postoyannymi chlenami skoplenii, dvizhushimisya vokrug centrov mass poslednih, a ne zvezdami, pokidayushimi skopleniya so skorostyami, prevyshayushimi skorost' otryva.

Konechno, za predelami ustoichivyh koron dolzhno nablyudat'sya nekotoroe kolichestvo zvezd, deistvitel'no pokinuvshih skoplenie i udalyayushihsya ot nego. Eti zvezdy ne dolzhny prinimat'sya vo vnimanie pri opredelenii istinnyh razmerov skopleniya. Vyyavlenie ih vozmozhno v nastoyashee vremya tol'ko putem analiza sobstvennyh dvizhenii zvezd v samyh shirokih okrestnostyah naibolee blizkih k Solncu skoplenii.

Dinamicheskaya ustoichivost' sistemy "yadro - korona" v celom svidetel'stvuet o tom, chto korona yavlyaetsya stol' zhe neot'emlemoi strukturnoi osobennost'yu lyubogo skopleniya, kak i ego yadro. S etoi tochki zreniya my mozhem govorit' o edinstve stroeniya vseh zvezdnyh skoplenii, kotoroe stanovitsya osobenno ochevidnym pri sopostavlenii mezhdu soboi krivyh raspredeleniya prostranstvennoi zvezdnoi plotnosti v razlichnyh sistemah.

<< 8.4 Yadra i korony - osnovnye oblasti zvezdnyh skoplenii | Oglavlenie | 8.6 Edinstvo stroeniya zvezdnyh skoplenii. Logarifmicheskii diapazon plotnostei >>

Publikacii s klyuchevymi slovami: zvezdy - Skoplenie Publikacii so slovami: zvezdy - Skoplenie
Sm. takzhe: Chernaya dyra razrushaet zvezdu: animaciya Zvezdy, pyl' i tumannost' v NGC 6559 25 samyh yarkih zvezd na nochnom nebe Animaciya: chernaya dyra razrushaet zvezdu Kometa, skopleniya i tumannosti Sravnenie razmerov zvezd Samaya dalekaya iz vseh izvestnyh zvezd? Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce