Astronet > Zvezdnye skopleniya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Zvezdnye skopleniya << 8.8 Analiz raspredeleniya poverhnostnoi yarkosti v sharovyh skopleniyah. Krivye koncentracii izlucheniya | Oglavlenie | 9.1 Vvodnye zamechaniya >>

8.9 Obshie zakony raspredeleniya plotnosti v zvezdnyh skopleniyah. Zakon Shustera. Zakon Kinga

Neodnokratno delalis' popytki naiti obshie zakony raspredeleniya plotnosti v zvezdnyh skopleniyah. Kak pravilo, pri etom rasseyannye i sharovye skopleniya rassmatrivalis' razdel'no. Pervye poiski obshego zakona raspredeleniya prostranstvennoi plotnosti zvezd v zvezdnyh skopleniyah byli svyazany s predstavleniem o vozmozhnosti provedeniya analogii mezhdu zvezdnymi skopleniyami i gazovymi sharami. Plammer (1911; 1916) approksimiroval raspredelenie plotnosti f(r), nablyudaemoe v yarkih sharovyh skopleniyah, izuchennyh Pikkeringom (1897) i Beili (1916), zakonom Shustera, predlozhennym poslednim dlya predstavleniya vnutrennego stroeniya zvezd:

$f(r) = f(0)[1+(\frac{r}{r_0})^2]^{-5/2},$ (8.33)

gde r₀ - nekotoraya postoyannaya. Populyarnosti etogo zakona, po spravedlivomu zamechaniyu Kosticyna (1922), nemalo sposobstvovala ego prostota. Poskol'ku zakon Shustera - Plammera udovletvoryal nablyudeniyam daleko ne vsegda (Ceipel', 1913; Kosticyn, 1922), voznikla neobhodimost' ego obobsheniya, vpervye predlozhennogo Vallenkvistom (1933):

$f(r) = f(0)[1+(\frac{r}{r_0})^2]^{-\beta},$ (8.34)

gde β - postoyannaya, mogushaya menyat'sya ot skopleniya k skopleniyu. Soglasno Lomanu (1964), rassmotrevshemu raspredelenie plotnosti v 67 rasseyannyh skopleniyah po dannym Vallenkvista (sm. nizhe), v 80% sluchaev ono udovletvoritel'no predstavlyaetsya zakonom (8.34) pri 2,0 < r < 4,4.

V 1959 g. Vallenkvist (1959) opublikoval rezul'taty svoei pochti tridcatiletnei raboty po izucheniyu struktury 67 rasseyannyh skoplenii. Ego issledovanie otnositsya, v sushnosti, kak my teper' znaem, tol'ko k yadram skoplenii i dazhe v ryade sluchaev lish' k vnutrennim zonam etih yader (za isklyucheniem Giad). Dlya odnorodnosti issledovaniya on podschityval zvezdy v predelah chetyreh velichin, nachinaya ot samyh yarkih.

Vallenkvist nashel, chto raspredelenie prostranstvennoi plotnosti v yadrah vseh skoplenii luchshe vsego predstavlyaetsya zakonom

$f(r) = f(0)(1-r)^c,$ (8.35)

gde rasstoyanie ot centra r vyrazhaetsya v dolyah radiusa skopleniya (vernee, v dolyah radiusa yadra), prinyatogo Vallenkvistom: 0 ≤ 1 - r ≤ 1.

Postoyannaya s nazyvaetsya stepen'yu koncentracii. Pri s = 0 f(r) ne zavisit ot r i ravna central'noi plotnosti f(0). Chem bol'she s, tem bystree izmenyaetsya f(r), tem sil'nee koncentriruyutsya zvezdy v yadre skopleniya k ego centru.

Korrelyacii velichin s s klassami koncentracii Tryumplera (1930a) ne obnaruzheno. Po-vidimomu, kak i v sluchae sharovyh skoplenii, nevozmozhno sravnivat' real'nye kolichestvennye pokazateli stepeni koncentracii s prostymi ocenkami etoi velichiny, osnovannymi na neposredstvennom zritel'nom vospriyatii vneshnego vida sistemy. Naibolee sushestvennoi zakonomernost'yu, obnaruzhennoi Vallenkvistom, yavlyaetsya uvelichenie stepeni koncentracii zvezd v yadre skopleniya k ego centru s uvelicheniem lineinyh razmerov yadra, chto svyazano, ochevidno, s rostom massy poslednego.

Pereidem teper' k rassmotreniyu raboty Kinga (1962), kotoromu udalos', po-vidimomu, naiti deistvitel'no obshii empiricheskii zakon raspredeleniya vidimoi plotnosti zvezd v zvezdnyh skopleniyah (kak sharovyh, tak i rasseyannyh.) i karlikovyh ellipticheskih galaktikah.

Okazalos', chto vidimaya plotnost' F(r) vo vneshnih chastyah proekcii sharovyh zvezdnyh skoplenii pa nebesnuyu sferu, ispravlennaya za plotnost' zvezd fona, menyaetsya s izmeneniem r po zakonu

$F(r) = F_1(\frac{1}{r} - \frac{1}{r_t})^2,$ (8.36)

gde F₁ = const, a r_t - znachenie r, pri kotorom F(r) = 0. Na grafike $\sqrt{F}, 1/r$ my dolzhny poluchit' pryamuyu liniyu. Na ris. 134 (King, 1962) izobrazhen hod F(r) po podschetam zvezd v sharovom skoplenii M 15. My vidim, chto zakon (8.36) horosho soblyudaetsya v naruzhnyh oblastyah skopleniya. Peresechenie poluchaemoi pryamoi linii s os'yu absciss opredelyaet radius skopleniya r_t, pri kotorom F(r) dostigaet nulya.

Ukloneniya ot zakona (8.36) na ris. 134 zametny pri 1/r > 1,5; dlya central'nyh chastei skoplenii on yavno neprimenim, tak kak tam on privodit k beskonechno bol'shim znacheniyam plotnostei, i nuzhno iskat' drugoi zakon.

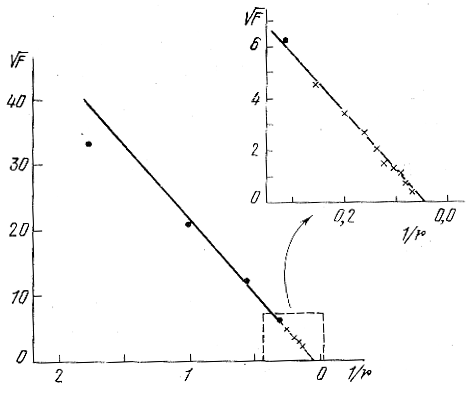
Ris. 134. Proverka zakona (8.36) po podschetam zvezd vo vneshnih oblastyah skopleniya M 15 (King, 1962).

Analiziruya dannye poverhnostnoi fotometrii Gaskoina i Barra (1956) dlya skopleniya 47 Tus, o kotoryh my uzhe govorili, King prishel k vyvodu, chto raspredelenie poverhnostnoi yarkosti F(r) v etom sluchae mozhno predstavit' formuloi

$F(r) = \frac{F_0}{1+(\frac{r}{r_c})^2},$ (8.37)

gde F₀ - central'naya poverhnostnaya yarkost', a r_s - tak nazyvaemyi masshtabnyi mnozhitel', kotoryi King nazyvaet radiusom serdceviny (core) skopleniya. Kak otmechaet King, radius r_s opredelyaetsya vnutrennei energiei sistemy, a radius r_t - vneshnimi prilivnymi silami. V svoe vremya Moubrei (1946) opredelil dlya 64 sharovyh skoplenii diametry d_0,5 ih izobrazhenii, pri kotoryh poverhnostnaya yarkost' padaet do poloviny central'noi poverhnostnoi yarkosti sistemy. Znacheniya r_s blizki k ½d_0,5. Eti znacheniya ne sootvetstvuyut znacheniyam radiusov yader skoplenii, opredelenie kotoryh dano nami v § 8.4. Tak, naprimer, dlya skopleniya M 3 my prinimaem, chto radius yadra raven 5',3. Sootvetstvuyushee znachenie d_0,5 Moubreya sostavlyaet 0',7.

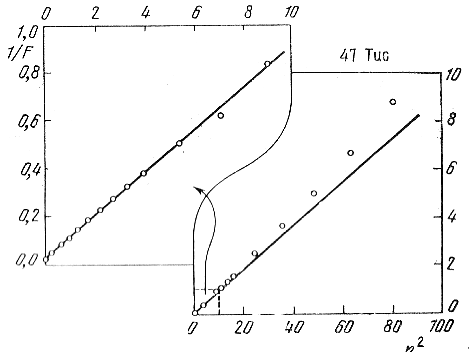
Ris. 135. Proverka zakona (8.37) po raspredeleniyu poverhnostnoi yarkosti v central'noi oblasti skopleniya 47 Tus (King, 1962).

V sushnosti, kak podcherkivayut Peterson i King (1975), gs yavlyaetsya radiusom oblasti pochti postoyannoi plotnosti bliz centra skopleniya, t. e. radiusom central'noi zony yadra, po nashei terminologii (sm. § 8.4). V samom dele, radius, central'noi zony yadra skopleniya M 3 po nashim dannym raven 0',5, chto blizko k privedennomu vyshe znacheniyu 0',7 ili k polovine ego. Esli otkladyvat' po osi ordinat 1/F, a po osi absciss r², to na grafike dolzhna poluchit'sya pryamaya liniya. Na ris. 135 (King, 1962) izobrazhen hod poverhnostnoi yarkosti v central'noi oblasti skopleniya 47 Tus. Ot 0 do 5' nablyudeniya dostatochno horosho soglasuyutsya s zakonom (8.37). Sootnoshenie zhe (8.36) udovletvoryaet v dannom sluchae nablyudeniyam ot granic skopleniya do 2' ot ego centra.

Pozzhe King (1966b) opublikoval rezul'taty fotoelektricheskoi poverhnostnoi fotometrii vnutrennih oblastei devyati yarkih sharovyh skoplenii, podtverdivshie pravil'nost' formuly (8.37). Edinaya formula, ob'edinyayushaya svoistva obeih formul i predstavlyayushaya raspredelenie plotnosti vo vsem skoplenii, imeet vid

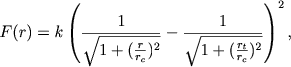
$F(r) = k\left(\frac{1}{\sqrt{1+(\frac{r}{r_c})^2}} - \frac{1}{\sqrt{1+(\frac{r_t}{r_c})^2}}\right)^2,$ (8.38)

V tipichnom sharovom skoplenii r_t/r_c ≈ 30. Esli r/r_c malo ili ne ochen' veliko, to, vynosya v (8.38) pervyi chlen za skobki, poluchaem vyrazhenie (8.37) s

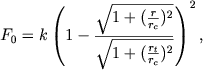
$F_0 = k\left(1 - \frac{\sqrt{1+(\frac{r}{r_c})^2}}{\sqrt{1+(\frac{r_t}{r_c})^2}}\right)^2,$

gde raznost' v skobkah ne ochen' sil'no otlichaetsya ot 1. Vyrazhenie (8.38) mozhno zapisat' takzhe v vide

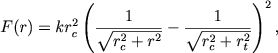
$F(r) = kr_c^2 \left(\frac{1}{\sqrt{r_c^2+r^2}} - \frac{1}{\sqrt{r_c^2+r_t^2}}\right)^2,$ (8.39)

pokazyvayushem, chto pri r 》 r_c i r_t 》 r_c ono perehodit v vyrazhenie (8.36) s F₁ = kr_c².

Dlya sravneniya zakona (8.38) s nablyudeniyami King postroil standartnye krivye lgF(r) dlya raznyh znachenii logarifma parametra s = r_t/r_c, kotoryi mozhno nazyvat' prosto koncentraciei. Eti krivye izobrazheny na ris. 136 i 137 (King, 1962). Ris. 136 udoben dlya analiza raspredeleniya plotnosti vo vnutrennih oblastyah skoplenii, ris. 137 - vo vneshnih.

Znacheniya s zaklyucheny v predelah ot 3,5 do 125. Oni dovol'no horosho korreliruyut s tremya klassami koncentracii izlucheniya, naidennymi Kronom i Meiallom (1960). Chem bol'she znachenie s, tem vyshe koncentraciya zvezd k centru sistemy. V to zhe vremya, kak i sledovalo ozhidat', korrelyaciya etogo parametra s klassami koncentracii Shepli - Soier i Moubreya (sm. § 2.3) ochen' slaba.

Rezul'taty podschetov zvezd i krivye lgF(r), lgr dlya 54 sharovyh skoplenii privedeny v stat'e Kinga i dr. (1968), a eshe dlya 23 skoplenii - v stat'e Petersona (1976). Znacheniya r_t i r_c dlya bol'shogo chisla skoplenii mozhno naiti v stat'yah Petersona i Kinga (1975), a takzhe Petersona (1976), v kotoryh v kachestve parametra koncentracii s prinimaetsya uzhe ne znachenie r_t/r_c, a lg(r_t/r_c).

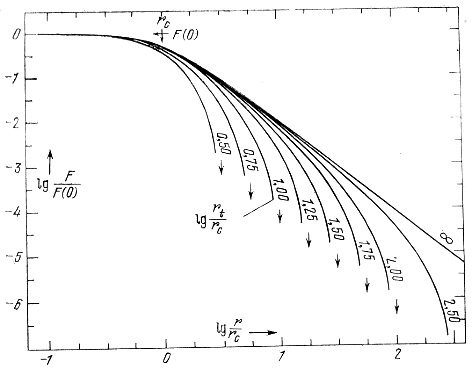
Ris. 136. Krivye raspredeleniya vidimoi plotnosti vo vnutrennih oblastyah skoplenii dlya raznyh znachenii parametra koncentracii s (King, 1962).

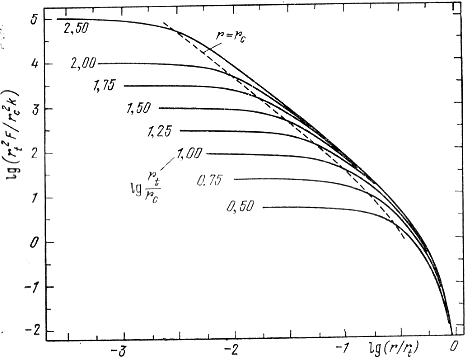
Ris. 137. Krivye raspredeleniya vidimoi plotnosti vo vneshnih oblastyah skoplenii dlya raznyh znachenii parametra koncentracii s (King, 1962).

Sravnim ris. 136 i 137 s ris. 128 i 129 (sm. § 8.6). Hotya v pervom; sluchae my imeem delo s krivymi F(r), a vo vtorom - s f(r), risunki ochen' shodny. Formuly (8.21) i ris. 120 pokazyvayut, chto znacheniya f(r) ≈ 0,1F(r). Nesomnenno, kak te, tak i drugie krivye illyustriruyut odni i te zhe zakonomernosti stroeniya zvezdnyh skoplenii. Krivye Kinga, estestvenno, bolee sglazheny.

Po analogii s obobsheniem zakona Shustera Veltmann (1965a) predlozhil svoeobraznoe obobshenie formuly Kinga (8.38):

$F(r) = F_0 \left(\frac{1}{[1+(\frac{r}{r_0})^{\gamma}]^{\beta / k}} - \frac{1}{[1+(\frac{r_t}{r_0})^{\gamma}]^{\beta / k}}\right)^k,$ (8.40)

gde k, β, γ - nekotorye postoyannye. Sootnoshenie (8.40) perehodit v (8.38)) pri k = 2, β = 1, γ = 2. Odnako vryad li formula (8.40) primenyalas' na praktike pri drugih znacheniyah postoyannyh.

King (1962) nashel takzhe obshii zakon raspredeleniya prostranstvennoi plotnosti f(r) vo vsem skoplenii putem podstanovki vyrazheniya (8.38) v reshenie uravneniya Abelya (8.7):

$f(r) = \frac{k/z^2}{\pi r_c [1+(\frac{r_t}{r_c})^2]^{3/2}} \Bigl [\frac{1}{z} \arccos z - \sqrt{1-z^2} \Bigl ],$ (8.41)

gde $z = [1+(\frac{r}{r_c})^2]^{1/2} [1+(\frac{r_t}{r_c})^2]^{-1/2}$ .

Etot zakon ispol'zuetsya pri provedenii issledovanii, posvyashennyh dinamike zvezdnyh skoplenii.

Eshe odin zakon raspredeleniya plotnosti, - v tak nazyvaemyh izohronnyh skopleniyah, - budet rassmotren v sleduyushei glave (§ 9.3) v svyazi s opisaniem dinamicheskih svoistv zvezdnyh skoplenii, nerazryvno svyazannyh s ih strukturnymi osobennostyami.

V zaklyuchenie - neskol'ko zamechanii o kuboidal'nyh zvezdnyh skopleniyah (sm. Karsdem, 1974). Do sih por ne udalos' obnaruzhit' ni odnogo takogo skopleniya. Poetomu Karsdem ne nashel nikakih priznakov togo, chto eti skopleniya koncentriruyutsya k galakticheskoi ploskosti, a takzhe prishel k ne sovsem, pravda, ubeditel'nomu vyvodu, chto vsya sovokupnost' dannyh ob etih ob'ektah ne podtverzhdaet ves'ma rasprostranennuyu gipotezu ob obrazovanii zvezd iz oblakov mezhzvezdnoi sredy.

<< 8.8 Analiz raspredeleniya poverhnostnoi yarkosti v sharovyh skopleniyah. Krivye koncentracii izlucheniya | Oglavlenie | 9.1 Vvodnye zamechaniya >>

Publikacii s klyuchevymi slovami: zvezdy - Skoplenie Publikacii so slovami: zvezdy - Skoplenie
Sm. takzhe: Chernaya dyra razrushaet zvezdu: animaciya Zvezdy, pyl' i tumannost' v NGC 6559 25 samyh yarkih zvezd na nochnom nebe Animaciya: chernaya dyra razrushaet zvezdu Kometa, skopleniya i tumannosti Sravnenie razmerov zvezd Samaya dalekaya iz vseh izvestnyh zvezd? Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce