Astronet > Zvezdnye skopleniya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Zvezdnye skopleniya << 9.1 Vvodnye zamechaniya | Oglavlenie | 9.3 Dvizhenie zvezd v pole regulyarnyh sil sfericheskogo zvezdnogo skopleniya >>

9.2 Osnovnye uravneniya i obshie integraly dvizheniya. Tozhdestvo Lagranzha - Yakobi

Ris. 138. Shema, poyasnyayushaya vyvod formul (9.1) - (9.4).

Rassmotrim uravneniya dvizheniya zvezd v izolirovannom zvezdnom skoplenii, sostoyashem iz n zvezd s raznymi massami m₁, m₂, ..., m_n. Pust' r_ij - rasstoyanie mezhdu dvumya iz nih, imeyushimi massy m_i i m_j (ris. 138). Po zakonu N'yutona oni prityagivayutsya drug k drugu s siloi Gm_im_ir_ij^-2. Na zvezdu m_i so storony zvezdy m_j deistvuet sila s komponentami $-Gm_i m_j(x_i - x_j)r_{ij}^{-3}, \quad -Gm_i m_j(y_i - y_j)r_{ij}^{-3}, \quad -Gm_i m_j(z_i - z_j)r_{ij}^{-3}$ . Eti komponenty mozhno vyrazit' cherez velichinu $\Omega_{ij} = -Gm_im_jr_{ij}^{-1}$ , t. e. potencial'nuyu energiyu zvezdy m_i otnositel'no zvezdy m_j: $-\frac{\partial\Omega_{ij}}{\partial x_i}, \quad -\frac{\partial\Omega_{ij}}{\partial y_i}, \quad -\frac{\partial\Omega_{ij}}{\partial z_i}$ . Vse zvezdy skopleniya deistvuyut na zvezdu m_i s siloi, komponenty kotoroi ravny $-\frac{\partial\Omega_{i}}{\partial x_i}, \quad -\frac{\partial\Omega_{i}}{\partial y_i}, \quad -\frac{\partial\Omega_{i}}{\partial z_i}$ , gde

$\Omega_i = \sum\limits_j \Omega_{ij} = -Gm_i \sum\limits_j \frac{m_j}{r_{ij}}$ (9.1)

pri j ≠ i, Ω;;;_i - potencial'naya energiya zvezdy m_i.

Potencial'naya energiya vsego skopleniya, t. e. energiya vzaimnogo prityazheniya vseh zvezd skopleniya,

$\Omega = -G \sum\limits_{i \ne j} \frac{m_im_j}{r_{ij}}$ (9.2)

gde summirovanie proizvoditsya po vsem razlichnym param zvezd. Netrudno videt', chto

$\Omega = \frac{1}{2}\sum\limits_i \Omega_{i}.$ (9.3)

Differencial'nye uravneniya dvizheniya zvezd skopleniya imeyut vid

$m_i \ddot x_i = -\frac{\partial\Omega}{\partial x_i}, \quad m_i \ddot y_i = -\frac{\partial\Omega}{\partial y_i}, \quad m_i \ddot z_i = -\frac{\partial\Omega}{\partial z_i},$ (9.4)

gde i = 1, 2, ..., n. Integriruya sistemu etih uravnenii, mozhno poluchit' 10 obshih integralov dvizheniya, t. e. sootnoshenii, svyazyvayushih mezhdu soboi iskomye funkcii x_i(t), y_i(t), z_i(t) i prinimayushih postoyannoe znachenie, esli v nih vmesto neizvestnyh funkcii podstavit' reshenie sistemy. Shest' iz nih - integraly dvizheniya centra mass skopleniya, pokazyvayushie, chto v absolyutnoi sisteme koordinat on dvizhetsya ravnomerno i pryamolineino v nekotorom napravlenii. Tri iz nih - eto integraly ploshadei ili uglovyh momentov:

$\sum\limits_i m_i(y_i\dot z_i - z_i\dot y_i) = c_1, \quad \sum\limits_i m_i(z_i\dot x_i - x_i\dot z_i) = c_2, \quad \sum\limits_i m_i(x_i\dot y_i - y_i\dot x_i) = c_3,$ (9.5)

gde s₁, s₂, s₃ - postoyannye. Nakonec, desyatyi integral - eto integral energii

$\frac{1}{2}\sum\limits_i m_i (\dot x_i^2 + \dot y_i^2 + \dot z_i^2) + \Omega = h,$ (9.6)

gde h - postoyannaya energii, oznachayushii, chto vo vremya dvizheniya izolirovannoi sistemy polnaya energiya ee E, yavlyayushayasya summoi kineticheskoi (T) i potencial'noi energii (Ω;;;), ostaetsya postoyannoi.

Esli rassmatrivat' dvizhenie zvezd skopleniya otnositel'no centra ego mass, imeyushego koordinaty $\bar x, \, \bar y, \, \bar z$ i vvesti koordinaty zvezd otnositel'no etogo centra $\xi_i = x_i - \bar x, \, \eta_i = y_i - \bar y, \, \zeta_i = z_i - \bar z$ , to dlya opisaniya dvizheniya ostanutsya tol'ko tri integrala ploshadei i integral energii, kotorye primut vid

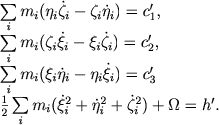
$\begin{array}{l} \sum\limits_i m_i (\eta_i\dot \zeta_i - \zeta_i\dot \eta_i) = c'_1, \\ \sum\limits_i m_i (\zeta_i\dot \xi_i - \xi_i\dot \zeta_i) = c'_2, \\ \sum\limits_i m_i (\xi_i\dot \eta_i - \eta_i\dot \xi_i) = c'_3 \\ \frac{1}{2}\sum\limits_i m_i (\dot \xi_i^2 + \dot\eta_i^2 + \dot \zeta_i^2) + \Omega = h'. \end{array}$ (9.7)

Krome togo, v etoi sisteme otscheta vsegda udovletvoryaetsya tak nazyvaemoe tozhdestvo Lagranzha - Yakobi

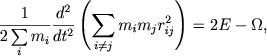
$\frac{1}{2\sum\limits_i m_i}\frac{d^2}{dt^2}\left(\sum\limits_{i \ne j} m_i m_j r_{ij}^2\right) = 2E - \Omega,$ (9.8)

iz kotorogo mozhno izvlech' neobhodimoe uslovie ustoichivosti zvezdnogo skopleniya. V samom dele, velichina Ω;;; vsegda otricatel'na; sledovatel'no, esli E > 0, to 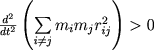$\frac{d^2}{dt^2}\left(\sum\limits_{i \ne j} m_i m_j r_{ij}^2\right) > 0$ , t.e vyrazhenie 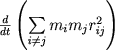$\frac{d}{dt}\left(\sum\limits_{i \ne j} m_i m_j r_{ij}^2\right)$ neogranichenno vozrastaet s techeniem vremeni. Dazhe esli ono pervonachal'no bylo otricatel'nym, to cherez nekotoroe vremya stanet polozhitel'nym, i velichina $\sum\limits_{i \ne j} m_i m_j r_{ij}^2$ nachnet vozrastat'. Eto znachit, chto po krainei mere odno iz rasstoyanii r_ij budet stremit'sya k beskonechnosti.

Takim obrazom, neobhodimym (no ne dostatochnym) usloviem ustoichivosti zvezdnogo skopleniya yavlyaetsya otricatel'nost' ego polnoi energii: E < 0. Esli E > 0, sistema ne mozhet byt' dinamicheski ustoichivoi, stacionarnoi.

Pol'zuyas' metodami klassicheskoi nebesnoi mehaniki dlya opisaniya obshih dinamicheskih svoistv skoplenii, my mozhem opirat'sya tol'ko na privedennye vyshe integraly ploshadei, energii i tozhdestvo Lagranzha - Yakobi, dayushie lish' samoe obshee predstavlenie ob etih svoistvah. Chtoby poluchit' bolee konkretnye predstavleniya o dinamicheskoi evolyucii skoplenii, mozhno idti dvumya putyami. Pervyi iz nih - eto primenenie k zvezdnym skopleniyam metodov statisticheskoi fiziki, vtoroi - chislennoe integrirovanie s pomosh'yu EVM strogih uravnenii dvizheniya n tel pri raznyh nachal'nyh usloviyah.

V pervom sluchae ispol'zuetsya ponyatie fazovoi plotnosti sistemy, t. e. funkcii raspredeleniya chisla ee chlenov v edinice ob'ema fazovogo shestimernogo prostranstva (koordinat i skorostei) kak funkcii vremeni, udovletvoryayushei uravneniyu Bol'cmana (sm., naprimer, Ogorodnikov, 1958, s. 243).

Nesmotrya na bol'shie uspehi, dostignutye na puti ispol'zovaniya EVM, vozmozhnosti EVM eshe ogranicheny, i s ih pomosh'yu do sih por udaetsya strogo analizirovat' povedenie sistem, chislo chlenov kotoryh n ≲ 500 (Vilen, 1974). Poetomu po-prezhnemu prodolzhaetsya razvitie statisticheskih metodov resheniya problemy, rezul'taty primeneniya kotoryh neploho soglasuyutsya s rezul'tatami, poluchennymi s pomosh'yu EVM.

Prezhde chem pereiti k opisaniyu statisticheskih metodov, rassmotrim dvizhenie zvezd v pole regulyarnyh sil skopleniya, opredelyaemom tol'ko ego potencialom.

<< 9.1 Vvodnye zamechaniya | Oglavlenie | 9.3 Dvizhenie zvezd v pole regulyarnyh sil sfericheskogo zvezdnogo skopleniya >>

Publikacii s klyuchevymi slovami: zvezdy - Skoplenie Publikacii so slovami: zvezdy - Skoplenie
Sm. takzhe: Chernaya dyra razrushaet zvezdu: animaciya Zvezdy, pyl' i tumannost' v NGC 6559 25 samyh yarkih zvezd na nochnom nebe Animaciya: chernaya dyra razrushaet zvezdu Kometa, skopleniya i tumannosti Sravnenie razmerov zvezd Samaya dalekaya iz vseh izvestnyh zvezd? Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce