Astronet > Zvezdnye skopleniya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Zvezdnye skopleniya << 9.2 Osnovnye uravneniya i obshie integraly dvizheniya. Tozhdestvo Lagranzha - Yakobi | Oglavlenie | 9.4 Irregulyarnye sily. Maksvellovo raspredelenie skorostei. Teorema viriala. Dinamicheskie massy skoplenii >>

9.3 Dvizhenie zvezd v pole regulyarnyh sil sfericheskogo zvezdnogo skopleniya

Esli prenebrech' deistviem irregulyarnyh sil (vliyaniem blizkih i dalekih sblizhenii zvezd s drugimi chlenami skopleniya), mozhno opredelit' traektoriyu zvezdy, opisyvaemuyu eyu pod deistviem regulyarnoi sily, obuslovlennoi sglazhennym gravitacionnym polom vsego skopleniya. Etu traektoriyu inogda nazyvayut regulyarnoi orbitoi. Rassmotrim regulyarnye orbity zvezd v sfericheskom skoplenii, koncentriruyushemsya k centru. Reshenie zadachi svoditsya k analizu dvizheniya material'noi tochki s massoi m vokrug tochki s peremennoi massoi M(r) (sm., naprimer, E. Stremgren, 1916).

Esli f(r) - prostranstvennaya plotnost' zvezd v skoplenii na rasstoyanii r ot ego centra, to massa skopleniya, zaklyuchennaya v sfere radiusa r,

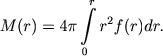
$M(r) = 4\pi\int\limits_0^r r^2 f(r)dr.$ (9.9)

Esli f(r) izmenyaetsya po zakonu Shustera (8.33), to, prinimaya v nem dlya prostoty f(0) = 1, r₀ = 1, mozhno napisat'

$f(r) = \frac{1}{(1+r^2)^{5/2}}.$ (9.10)

V takom sluchae M(r) legko vychislyaetsya po formule

$M(r) = \frac{4\pi}{3}\frac{r^3}{(1+r^2)^{3/2}},$ (9.11)

sila K(r), prityagivayushaya zvezdu m k centru takogo skopleniya, izmenyaetsya po zakonu

$K(r) = \frac{GmM(r)}{r^2} = \frac{4\pi}{3}\frac{Gmr}{(1+r^2)^{3/2}},$ (9.12)

Teper' mozhno napisat' sistemu differencial'nyh uravnenii dvizheniya i prointegrirovat' ee.

Poluchaemye pri etom regulyarnye orbity zvezd imeyut vid ellipsov s vrashayushimisya liniyami apsid (ris. 139). Vozmozhny takzhe ustoichivye krugovye orbity i dvizheniya po pryamym, prohodyashim cherez centr mass skopleniya. Ploskosti orbit vo vseh sluchayah prohodyat cherez centr.

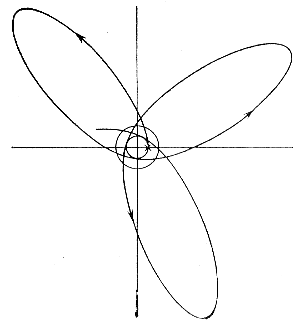
Ris. 139. Regulyarnaya orbita zvezdy v sharovom skoplenii (E. Stremgren, 1916).

Tochnoe reshenie uravnenii dvizheniya zvezdy okazyvaetsya vozmozhnym takzhe v bolee obshem sluchae tak nazyvaemyh izohronnyh skoplenii, rassmotrennyh, v chastnosti, Enonom (1959a; 1959b; 1960a). Potencial takih skoplenii opredelyaetsya vyrazheniem

$\Phi (r) = \frac{(2r^2 + 1 - \sqrt{4r^2 + 1})}{2r^2}.$ (9.13)

V obshem sluchae orbital'nyi period zvezdy v skoplenii zavisit ot ee polnoi energii E i uglovogo momenta. V izohronnom skoplenii on zavisit tol'ko ot velichiny E. Prostranstvennaya plotnost' f(r) pri etom nahoditsya iz vyrazheniya

$4\pi Gf(r) = \frac{2[1-\Phi (r)]^4[3+\Phi (r)]}{[1+\Phi (r)]^3},$ (9.14)

a vidimaya F(r) - po formule

$4\pi GF(r) = \frac{1}{r^3} \left(\arctg 2r - \frac{2r}{1+4r^2} \right).$ (9.15)

Nablyudaemoe raspredelenie F(r) v sharovyh skopleniyah M 5, M 15, M 92, ω Sen i 47 Tus neploho predstavlyaetsya formuloi (9.15). Orbity zvezd v izohronnyh skopleniyah shodny s izobrazhennoi na ris. 139. Obobshennye izohronnye modeli skoplenii byli predlozheny Veltmannom (1965b), a takzhe Kuzminym i Veltmannom (1972). Na ih opisanii my uzhe ne mozhem ostanavlivat'sya.

<< 9.2 Osnovnye uravneniya i obshie integraly dvizheniya. Tozhdestvo Lagranzha - Yakobi | Oglavlenie | 9.4 Irregulyarnye sily. Maksvellovo raspredelenie skorostei. Teorema viriala. Dinamicheskie massy skoplenii >>

Publikacii s klyuchevymi slovami: zvezdy - Skoplenie Publikacii so slovami: zvezdy - Skoplenie
Sm. takzhe: Chernaya dyra razrushaet zvezdu: animaciya Zvezdy, pyl' i tumannost' v NGC 6559 25 samyh yarkih zvezd na nochnom nebe Animaciya: chernaya dyra razrushaet zvezdu Kometa, skopleniya i tumannosti Sravnenie razmerov zvezd Samaya dalekaya iz vseh izvestnyh zvezd? Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce