Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu Zvezdnye skopleniya << 9.3 Dvizhenie zvezd v pole regulyarnyh sil sfericheskogo zvezdnogo skopleniya | Oglavlenie | 9.5 Vremya relaksacii. Dissipaciya zvezdnyh skoplenii >>

9.4 Irregulyarnye sily. Maksvellovo raspredelenie skorostei. Teorema viriala. Dinamicheskie massy skoplenii

V real'nyh zvezdnyh skopleniyah vremya ot vremeni proishodyat tesnye sblizheniya dvuh ili neskol'kih zvezd v processe dvizheniya ih po regulyarnym orbitam. Pri etom vzaimnye uskoreniya, ispytyvaemye zvezdami, uchastvuyushimi v sblizheniyah, po poryadku velichiny okazyvayutsya sravnimymi s uskoreniyami etih zvezd, obuslovlennymi deistvuyushei na nih regulyarnoi siloi.

Sily, voznikayushie v rezul'tate zvezdnyh sblizhenii, prinyato nazyvat' irregulyarnymi. Oni deistvuyut kratkovremenno i za vremya sblizheniya menyayut tol'ko otnositel'nye skorosti uchastvuyushih v nem zvezd. Oni nosyat sluchainyi harakter v tom smysle, chto rezul'tat kazhdogo sblizheniya ne zavisit ot rezul'tatov predydushego.

Narushaya dvizhenie zvezd po regulyarnym orbitam, irregulyarnye sily v to zhe vremya ustanavlivayut statisticheskoe raspredelenie ostatochnyh skorostei zvezd, t. e. raspredelenie, podchinyayusheesya nekotoromu statisticheskomu zakonu (pod ostatochnymi skorostyami v dannom sluchae podrazumevayutsya skorosti zvezd otnositel'no centra mass skopleniya). Esli pri etom deistvii irregulyarnyh sil vse harakteristiki skopleniya ostayutsya neizmennymi s techeniem vremeni, to govoryat, chto skoplenie nahoditsya v sostoyanii statisticheskogo ravnovesiya ili v statisticheski stacionarnom sostoyanii. Zvezdnye sblizheniya v skopleniyah igrayut tu zhe rol', chto i stolknoveniya molekul v gazah, blagodarya kotorym v gazah ustanavlivaetsya naiveroyatneishii statisticheskii zakon raspredeleniya skorostei Maksvella. Ispol'zuya metody statisticheskoi mehaniki, zvezdnaya dinamika pokazyvaet, chto pri dostatochno bol'shom chisle zvezd naiveroyatneishim zakonom raspredeleniya ih ostatochnyh skorostei v statisticheski stacionarnom skoplenii yavlyaetsya tot zhe zakon Maksvella:

$$ dN = N\left(\frac{j}{\sqrt\pi}\right)^3\exp(-j^2[v_\xi^2 + v_\eta^2 + v_\zeta^2])dv_\xi dv_\eta dv_\zeta , $$ (9.16)

gde dN - chislo zvezd v elemente ob'ema prostranstva skorostei dvξdvηdvζ, N - polnoe chislo zvezd skopleniya, vξ, vη, vζ - komponenty ostatochnyh skorostei v zvezd,

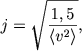
$$ j = \sqrt{\frac{1,5}{\langle v^2 \rangle}}, $$ (9.17)

a $\sqrt{\langle v^2 \rangle}$ - srednyaya kvadratichnaya skorost' zvezd skopleniya, harakterizuyushaya dispersiyu skorostei etih zvezd. Simvolom 〈〉 zdes' i v dal'neishem my budem oboznachat' srednee znachenie. Esli prointegrirovat' vyrazhenie (9.16) po beskonechno tonkomu sfericheskomu sloyu v prostranstve skorostei, to poluchitsya inaya forma zapisi zakona Maksvella:

$$ n(v)dv = \frac{4Nj^3}{\sqrt\pi}e^{-j^2v^2}v^2dv. $$ (9.18)

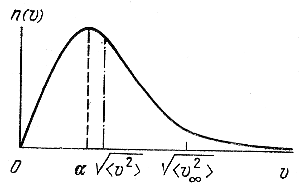
zdes' n(v)dv - chislo zvezd, skorosti kotoryh zaklyucheny n intervale ot v do v+dv. Grafik sootvetstvuyushei krivoi n(v) izobrazhen na ris. 140. Maksimum ee sootvetstvuet naibolee veroyatnoi skorosti α, svyazannoi s parametrom j sootnosheniem α = j-1, a so srednei kvadratichnoi skorost'yu - sootnosheniem $\sqrt{\langle v^2 \rangle} = \sqrt{1,5}\alpha = \approx 1,22\alpha$.


Ris. 140. Shematicheskoe predstavlenie maksvellova zakona raspredeleniya skorostei.

V statisticheski stacionarnom skoplenii $\sum\limits_{i \ne j} m_im_jr_{ij}^2 = const$. Iz tozhdestva Lagranzha - Yakobi (9.8) v etom sluchae vytekaet, chto

$$ 2E - \Omega = 0; \quad 2T + \Omega = 0. $$ (9.19)

Eto tak nazyvaemaya teorema viriala: v statisticheski stacionarnoi sisteme ee potencial'naya energiya, vzyataya s protivopolozhnym znakom, ravna udvoennoi kineticheskoi energii ee chlenov, a udvoennaya polnaya energiya ravna potencial'noi. V statisticheski stacionarnom zvezdnom skoplenii srednyaya kvadratichnaya skorost' zvezd svyazana s ego massoi M. Eta svyaz' vytekaet iz teoremy viriala. Dlya prostoty dopustim, chto vse chleny skopleniya imeyut odinakovye massy m. Togda M = Nm,

$$ 2T = M\langle v^2 \rangle, $$ (9.20)

a sootnoshenie (9.2) mozhno zapisat' v vide

$$ \Omega = -\frac{1}{2}\frac{Gm^2N(N-1)}{\bar R}, $$ (9.21)

gde

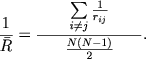
$$ \frac{1}{\bar R} = \frac{\qquad\sum\limits_{i \ne j}\frac{1}{r_{ij}}\qquad}{\frac{N(N-1)}{2}}. $$ (9.22)

Velichina $\bar R$ mozhet byt' nazvana srednim effektivnym radiusom skopleniya. Ee obratnaya velichina yavlyaetsya srednim znacheniem obratnyh velichin vzaimnyh rasstoyanii mezhdu vsemi chlenami skopleniya. Prakticheski za $\bar R$ prinimayut radius okruzhnosti, soderzhashei v proekcii na ploskost' polovinu massy skopleniya (King, 1958a). Prenebregaya pri bol'shom N edinicei v chislitele vyrazheniya (9.21) i prinimaya vo vnimanie sootnosheniya (9.19), (9.20) i (9.21), nahodim

$$ \langle v^2 \rangle = \frac{1}{2}\frac{GM}{\bar R}. $$ (9.23)

Esli vyrazit' M v edinicah massy Solnca, a $\bar R$ - v parsekah, to

$$ \sqrt{\langle v^2 \rangle} = 0,0463\sqrt{\frac{M}{\bar R}} \, \mbox{km/s}. $$ (9.24)

Po etoi formule, znaya znacheniya M i $\bar R$, mozhno opredelyat' dispersiyu skorostei zvezd v skoplenii, a opredeliv iz nablyudenii dispersiyu skorostei i velichinu $\bar R$, naiti massu skopleniya M. Mozhno predlozhit' i drugie modifikacii formuly (9.24), zavisyashie ot prinyatogo zakona raspredeleniya plotnosti zvezd (ili massy) v skoplenii (sm.,naprimer, Kurt, 1951).

V yadrah tipichnyh rasseyannyh skoplenii dispersiya skorostei zvezd blizka k ± 0,5 km/s. V chastnosti, dlya Pleyad (Titus, 1938), ona sostavlyaet ± 0,59 km/s, a dlya skopleniya Yasli (Shilt, Titus, 1938) ± 0,79 km/s. Sootvetstvuyushie znacheniya mass etih skoplenii okazyvayutsya ravnymi 510 i 730 mass Solnca (Miner, 1939; van Veik, 1949).

Shodnye znacheniya dispersii skorostei zvezd v etih skopleniyah poluchil Dzhons (1970a; 1970b; 1971), nashedshii neskol'ko bolee rafinirovannym metodom, chto sootvetstvuyushaya nablyudaemoi dispersii massa Pleyad dostigaet 690, a massa skopleniya Yasli - 560 mass Solnca.

Dispersiya luchevyh skorostei zvezd v sharovyh skopleniyah okazyvaetsya na poryadok vyshe (Vilson, Koffin, 1954; Shvarcshil'd, Bernstein, 1955; Fist, Tekkerei, 11)60; Harding, 1965). No oshibki luchevyh skorostei slabyh zvezd, opredelyavshihsya do nedavnego vremeni, byli stol' veliki, chto naidennye perechislennymi avtorami znacheniya dispersii mogli rassmatrivat'sya lish' kak verhnie predely znachenii istinnyh dispersii (Gunn, Griffin, 1979). Pravda, Harding (1965) po svoim izmereniyam obnaruzhil dazhe vrashenie skopleniya ω Sen, no, po-vidimomu, lish' v rabotah Illingvorsa (1976), a takzhe Da Kosty i dr. (1977), byli polucheny nadezhnye znacheniya dispersii skorostei zvezd v yadrah neskol'kih sharovyh skoplenii.

Gunn i Griffin (1979), ispol'zuya fotoelektricheskii spektrometr dlya izmereniya luchevyh skorostei zvezd, pozvolyayushii opredelyat' ih s tochnost'yu do 0,3 km/s, sumeli ne tol'ko opredelit' dispersiyu luchevyh skorostei zvezd v skoplenii M 3 ( ± 4,8 km/s), no i prosledit' za ee umen'sheniem s uvelicheniem rasstoyaniya ot centra skopleniya, chto svidetel'stvuet ob anizotropii polya skorostei vo vneshnih oblastyah etoi sistemy. Analiz etih nablyudenii i sochetanii s analizom razlichnyh modelei skoplenii, osnovannyh na nablyudaemom raspredelenii ego poverhnostnoi yarkosti, pozvolil im ocenit' znachenie polnoi massy M 3 (6 · 105 mass Solnca) s bol'shei tochnost'yu, chem eto mozhno bylo by sdelat' s pomosh'yu formuly (9.24).

Izmereniya Gunna i Griffina, provedennye dlya 111 zvezd skopleniya yarche 14m,0 V, pokazali takzhe otsutstvie spektral'no-dvoinyh sistem sredi krasnyh gigantov v M 3 i nalichie sluchainyh dvizhenii v atmosferah etih zvezd so skorostyami, dostigayushimi neskol'kih desyatyh kilometra v sekundu.

Sushestvovanie maksvellova raspredeleniya skorostei s ego "hvostom", uhodyashim v beskonechnost', pozvolyaet schitat', chto hotya i malaya, no konechnaya dolya polnogo chisla zvezd, skopleniya mozhet priobretat' skorosti, dostatochnye dlya preodoleniya prityazheniya so storony ostal'nyh chlenov sistemy. Naimen'shaya skorost', pri kotoroi zvezda navsegda pokidaet izolirovannoe skoplenie, nazyvaetsya parabolicheskoi skorost'yu, ili skorost'yu osvobozhdeniya, otryva ot skopleniya. Oboznachim ee simvolom v∞. Dlya togo, chtoby zvezda pokinula skoplenie, ee kineticheskaya energiya T∞, dolzhna byt' ne men'she energii ee gravitacionnogo vzaimodeistviya s ostal'nymi zvezdami skopleniya, t. e. vzyatoi s obratnym znakom ee potencial'noi energii. Oboznachim srednie znacheniya etih energii simvolami 〈T∞〉 i 〈Ω;;;i〉. Uslovie ravenstva sootvetstvuyushih velichin privodit k sootnosheniyu

$$ \langle v_{\infty}^2 \rangle = \frac{2GM}{\bar R}. $$ (9.25)

Sravnivaya (9.23) s (9.25), nahodim, chto

$$ \sqrt{\langle v_{\infty}^2 \rangle} = 2\sqrt{\langle v^2 \rangle}, $$ (9.26)

t. e. srednyaya kvadratichnaya skorost' osvobozhdeniya ravna udvoennomu znacheniyu srednei kvadratichnoi skorosti zvezd v skoplenii (sm. ris. 140). Teoreticheski v usloviyah strogogo statisticheskogo ravnovesiya dolzhno soblyudat'sya ravnoraspredelenie kineticheskoi energii mezhdu chlenami skopleniya, imeyushimi raznye massy:

$$ m_1\langle v^2(m_1) \rangle = m_2\langle v^2(m_2) \rangle, $$ (9.27)

Raschety na EVM, imitiruyushie dinamicheskuyu evolyuciyu sistemy (Vilen, 1967), pokazyvayut, odnako, chto v predostavlennoi samoi sebe sisteme gravitacionno vzaimodeistvuyushih n tel s raznymi massami ravnoraspredelenie kineticheskoi energii ne sohranyaetsya. Ob etom zhe svidetel'stvuyut i nablyudeniya. Tak, v Pleyadah dispersiya skorostei ne vozrastaet zametno s perehodom k zvezdam men'shih mass (Dzhons, 1970a).

Sleduyushim vazhnym ponyatiem, na kotoroe opiraetsya statisticheskaya teoriya dinamiki zvezdnyh skoplenii, yavlyaetsya ponyatie vremeni relaksacii.

<< 9.3 Dvizhenie zvezd v pole regulyarnyh sil sfericheskogo zvezdnogo skopleniya | Oglavlenie | 9.5 Vremya relaksacii. Dissipaciya zvezdnyh skoplenii >>
Publikacii s klyuchevymi slovami: zvezdy - Skoplenie
Publikacii so slovami: zvezdy - Skoplenie
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu
Ocenka: 2.7 [golosov: 172]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya