Astronet > Zvezdnye skopleniya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Zvezdnye skopleniya << 9.4 Irregulyarnye sily. Maksvellovo raspredelenie skorostei. Teorema viriala. Dinamicheskie massy skoplenii | Oglavlenie | 9.6 Izotermicheskie yadra skoplenii. Opredelenie otnositel'nyh mass zvezd v zvezdnyh skopleniyah >>

9.5 Vremya relaksacii. Dissipaciya zvezdnyh skoplenii

Pod vremenem relaksacii skopleniya τ v zvezdnoi dinamike prinyato podrazumevat' promezhutok vremeni, v techenie kotorogo v sisteme pod deistviem irregulyarnyh sil uspevaet vosstanovit'sya narushennoe maksvellovo raspredelenie skorostei. Chem bol'she τ, tem men'she vliyanie zvezdnyh sblizhenii na dvizhenie zvezd skopleniya. Na praktike dlya nahozhdeniya τ vvodyatsya razlichnye opredeleniya etogo ponyatiya. V rezul'tate sblizheniya dvuh zvezd nablyudaetsya otklonenie napravlenii ih dvizheniya ot pervonachal'nyh i obmen kineticheskimi energiyami Δ E mezhdu nimi. V dinamike zvezdnyh sistem (sm., naprimer, Chandrasekar, 1948) pokazyvaetsya, kak mozhno poluchit' formuly dlya vychisleniya velichiny &Sigma(Δ E)² dlya odnoi zvezdy i opredelit' zavisimost' etoi velichiny ot vremeni t. Kogda velichina $\sqrt{\langle \Sigma (\Delta E)^2 \rangle}$ stanovitsya sravnimoi s nachal'noi kineticheskoi energiei zvezdy, my govorim, chto vremya τ_E, neobhodimoe dlya etogo, est' vremya relaksacii skopleniya. Mozhno dat' i drugie opredeleniya vremeni relaksacii, naprimer, ocenit' vremya τ_D, v techenie kotorogo &Sigma sin²φ, gde φ - ugol otkloneniya zvezdy pri rassmatrivaemom sblizhenii ot pervonachal'nogo napravleniya dvizheniya, stanovitsya ravnoi 1. Pri vseh takih opredeleniyah znacheniya τ_E, τ_D i t. p. okazyvayutsya velichinami odnogo poryadka. Po Chandrasekaru (1948), s popravkoi Spitcera i Herma (1958),

$\tau = 0,1357\sqrt{\frac{N\bar R^3}{Gm}}\frac{1}{\ln \frac{N}{2}},$ (9.28)

gde N - chislo zvezd v skoplenii, $\bar R$ - ego srednii effektivnyi radius, opredelyaemyi sootnosheniem (9.22), m - massa zvezdy, prinimaemaya odinakovoi dlya vseh chlenov skopleniya, G - postoyannaya tyagoteniya. Eta formula vyvedena putem ispol'zovaniya srednei dispersii skorostei dlya vsego ob'ema skopleniya. Tak kak v deistvitel'nosti plotnost' v skoplenii bystro ubyvaet s udaleniem ot ego centra, sblizheniya mezhdu zvezdami dolzhny pri etom proishodit' rezhe, stanovyas' menee effektivnymi. Sootvetstvenno, v koronal'noi oblasti skopleniya vremya relaksacii dolzhno byt' bol'she, chem v oblasti yadra.

King (1958a; 1958v; 1959) pokazal, chto uchet koncentracii zvezd k centru skopleniya pri uslovii, chto plotnost' v skoplenii menyaetsya po zakonu Shustera, privodit k zamene chislovogo mnozhitelya v vyrazhenii (9.28) na 0,35, t. e. uvelichivaet vremya relaksacii skopleniya po sravneniyu s poluchaemym po formule (9.28) v 2,6 raza.

Raschet pokazyvaet, chto dlya yadra Pleyad, naprimer, τ = 8 · 10⁷ let. Tak kak vozrast etogo skopleniya blizok k 2 · 10⁷ let, mozhno dumat', chto v yadre ego eshe ne uspelo ustanovit'sya maksvellovo raspredelenie skorostei. Ne isklyucheno, odnako, chto vremya relaksacii pri obrazovanii skopleniya, v moment nachal'nogo kollapsa sistemy (sm. § 9.8), okazyvaetsya namnogo men'she vremeni relaksacii, sootvetstvuyushego nyneshnemu sostoyaniyu sistemy.

Pol'zuyas' ponyatiem vremeni relaksacii, mozhno ocenit' skorost' poteri zvezd skopleniem. Zvezdy, nahodyashiesya v "hvoste" maksvellova raspredeleniya, skorosti kotoryh prevyshayut skorost' otryva, pokidayut skoplenie. Raspredelenie skorostei, kak govoryat, yavlyaetsya usechennym pri skorosti otryva. Eto yavlenie imeet ogromnoe znachenie dlya evolyucii skoplenii. Vpervye ono bylo nezavisimo rassmotreno Ambarcumyanom (1938) i Spitcerom (1940). Oboznachim dolyu zvezd skopleniya, nahodyashihsya v hvoste maksvellova raspredeleniya skorostei, skorosti kotoryh prevyshayut parabolicheskuyu, bukvoi K. Proizvedya sootvetstvuyushee integrirovanie, netrudno naiti, chto K = 0,0074. Prinimaya, chto po istechenii vremeni relaksacii τ maksvellovo raspredelenie vosstanavlivaetsya i novye 0,74% zvezd skopleniya priobretayut skorosti, prevyshayushie skorost' otryva, mozhno naiti dolyu zvezd, pokidayushih skoplenie za edinicu vremeni (K/τ); skorost' poteri zvezd skopleniem opredelitsya uravneniem

$\frac{1}{N}\frac{dN}{dt} = -\frac{K}{\tau}.$ (9.29)

Polnyi raspad skopleniya dolzhen, kak kazhetsya, proizoiti za vremya, ne prevyshayushee τ/K. Odnako real'naya kartina dissipacii skopleniya, soprovozhdayushei ego dinamicheskuyu evolyuciyu, namnogo slozhnee.

King (1958a) perechislil ryad faktorov, vliyayushih na harakter i temp dissipacii, sovmestnyi uchet kotoryh eshe nevozmozhen. Nekotorye iz nih uzhe upomyanuty v § 9.1. Rassmotrim beglo ostal'nye faktory, izuchennye v dal'neishem Kingom (1958b; 1958v; 1959; 1960).

Tesnye sblizheniya zvezd, uchityvavshiesya pri pervyh issledovaniyah polei irregulyarnyh sil v skopleniyah, proishodyat sravnitel'no redko. Znachitel'nuyu rol' v pereraspredelenii energii mezhdu chlenami skopleniya igrayut slabye vzaimodeistviya zvezd, obuslovlennye ih dalekimi sblizheniyami, summarnoe vozdeistvie kotoryh na dvizhenie dannoi zvezdy mozhet byt' ochen' sushestvennym. Vpervye etot effekt byl uchten Chandrasekarom (1943a, b, v), kotoryi primenil tak nazyvaemoe uravnenie Fokkera - Planka dlya opisaniya izmenenii, vnosimyh dalekimi zvezdnymi sblizheniyami v raspredelenie skorostei zvezd.

Chandrasekar obratil vnimanie na to, chto zvezdy, priobretshie skorost', prevyshayushuyu skorost' otryva, ne obyazatel'no dolzhny pokinut' skoplenie, tak kak dal'neishie sblizheniya mogut zatormozit' ih dvizhenie. Chandrasekar (1943a) vvel dazhe ponyatie "dinamicheskogo treniya", pokazav, chto zvezdy, imeyushie bolee bystroe dvizhenie otnositel'no okruzhayushih, v srednem zamedlyayut svoe dvizhenie. King (1959) pokazal, chto sblizheniya uhodyashih zvezd s ostayushimisya uvelichivayut effektivnoe vremya relaksacii na vremya, trebuyusheesya dlya togo, chtoby uhodyashaya zvezda pokinula skoplenie. Dlya massivnyh skoplenii s bol'shim vremenem relaksacii etim effektom mozhno prenebrech', no dlya skoplenii s nebol'shim chislom chlenov on uvelichivaet effektivnoe vremya relaksacii na 10-30%. Sleduet imet' v vidu takzhe, chto uhod zvezd iz skopleniya proishodit nepreryvno, a ne posle togo, kak v hvoste maksvellova raspredeleniya nakaplivaetsya nuzhnyi procent zvezd so skorostyami, prevyshayushimi parabolicheskuyu.

Rezul'taty Chandrasekara, svyazannye s uchetom vliyanii dalekih sblizhenii, byli utochneny Spitcerom i Hermom (1958), a zatem Kingom (1960).

S drugoi storony, Enon (1960b) prishel k vyvodu, chto dalekie sblizheniya ne mogut privesti k priobreteniyu zvezdoi energii, prevyshayushei energiyu otryva, i vnov' podcherknul vazhnost' rassmotreniya blizkih sblizhenii dlya resheniya problemy dissipacii zvezdnyh skoplenii, na poryadok umen'shiv velichinu skorosti dissipacii, naidennuyu Kingom (1958a).

V svyazi s bol'shoi neopredelennost'yu podobnyh ocenok, rashodyashihsya mezhdu soboyu inogda na dva poryadka, my ne budem ostanavlivat'sya na opisanii drugih rabot, posvyashennyh etoi probleme; obzor mnogih iz nih mozhno naiti v uzhe upominavsheisya stat'e Petrovskoi (1968).

Do sih por my podrazumevali, chto skoplenie sostoit iz zvezd s odinakovymi massami. Odnako massy chlenov real'nyh zvezdnyh skoplenii razlichny. Nekotoroe predstavlenie o skorosti dissipacii zvezd raznyh mass iz zvezdnyh skoplenii dayut raboty Spitcera i Herma (1958), Agekyana (1959), Enona (1961), Vulli i Dikkensa (1962), a takzhe Michi (1963). Zvezdy, massa kotoryh na poryadok men'she srednei massy zvezd skopleniya, dissipiruyut iz skopleniya v 15-30 raz bystree zvezd srednei massy. Etomu vyvodu, odnako, protivorechat rezul'taty raschetov dinamicheskoi evolyucii modelei skoplenii (Vilen, 1967), soglasno kotorym procent zvezd, pokidayushih sformirovavsheesya skoplenie, ne zavisit ot ih massy (sm. § 9.8). Zvezdy znachitel'no bolee massivnye, chem zvezdy srednei massy, prakticheski ne pokidayut skopleniya. Esli oni sohranyayutsya v yadrah skoplenii v vide chernyh dyr, ih vliyanie na dinamicheskuyu evolyuciyu skopleniya bylo by trudno pereocenit'. No, po-vidimomu, postepenno oni vse zhe vybrasyvayutsya iz skoplenii pri kratnyh vzaimnyh sblizheniyah.

Eshe Spitcer (1940) otmetil, chto v processe dinamicheskoi evolyucii plotnoe izolirovannoe skoplenie, teryaya zvezdy, dolzhno szhimat'sya. Kolichestvenno etot process byl izuchen Gurevichem i Levinym (1950), Kingom (1958b) i Hernerom (1958). Rassmotrim hod rassuzhdenii Kinga.

Iz teoremy viriala (9.19) sleduet, chto

$E = \frac{1}{2}\Omega$ (9.30)

i

$\frac{1}{E}\frac{dE}{dt} = \frac{1}{\Omega}\frac{d\Omega}{dt} = \frac{L}{\tau},$ (9.31)

gde L - otnoshenie energii, unosimoi uhodyashimi zvezdami, nahodyashimisya v hvoste maksvellova raspredeleniya skorostei, k absolyutnomu znacheniyu polnoi energii E. Tak kak E < 0, ee absolyutnoe znachenie vozrastaet. Iz sootnosheniya (9.21) s zamenoi mnozhitelya N-1 na N vytekaet ravenstvo

$\frac{1}{\Omega}\frac{d\Omega}{dt} = \frac{2}{N}\frac{dN}{dt} - \frac{1}{\bar R}\frac{d\bar R}{dt}.$ (9.32)

Isklyuchaya τ iz sootnoshenii (9.29), (9.31) i (9.32), nahodim

$\frac{d\bar R}{\bar R} = \left(2+\frac{L}{K}\right)\frac{dN}{N},$ (9.33)

otkuda

$\frac{\bar R}{\bar R_0} = \left(\frac{N}{N_0}\right)^{2+\frac{L}{K}},$ (9.34)

gde $\bar R_0$ i N₀ - nachal'nye znacheniya $\bar R$ i N sootvetstvenno. Po etomu zakonu umen'shaetsya srednii effektivnyi radius izolirovannogo skopleniya s umen'sheniem chisla N ostayushihsya v nem zvezd.

Rassmotrim teper', kak menyaetsya τ s izmeneniem N. Sootnoshenie (9.28) s popravkami Kinga (1958a, v; 1959), opisannymi vyshe, prinimaet vid

$\tau = 0,35\sqrt{\frac{N\bar R^3}{Gm}}\frac{1}{\ln \frac{N}{2}}.$ (9.35)

Podstavlyaya syuda $\bar R$ iz sootnosheniya (9.34), nahodim

$\tau = \tau_0\left(\frac{N}{N_0}\right)^p\frac{\ln \frac{N_0}{2}}{\ln \frac{N}{2}},$ (9.36)

gde τ₀ est' nachal'noe znachenie τ (pri N = N₀, $\bar R$ = $\bar R_0$ ), a p = 7/2 + 3/2L/K.

Podstanovka vyrazheniya (9.36) v (9.29) pozvolyaet poluchit' differencial'noe uravnenie dlya opredeleniya zavisimosti N(t).

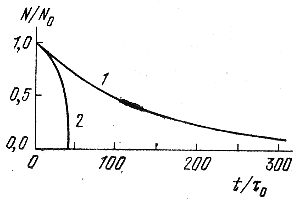
Ris. 141. Chislo zvezd, ostayushihsya v skoplenii s techeniem vremeni (King, 1958b).

Na ris. 141 (King, 1958b) pokazana poluchennaya Kingom dlya N₀ = 250 i r = 7/2 krivaya 2 izmeneniya otnosheniya N/N₀, s techeniem vremeni t/τ₀ v skoplenii, plotnost' v kotorom menyaetsya po zakonu Shustera. Process poteri zvezd idet s bol'shim uskoreniem. Krivaya 1, privedennaya dlya sravneniya na tom zhe risunke, sootvetstvuet eksponencial'nomu zakonu ubyvaniya chisla zvezd, kotoryi nablyudalsya by v sluchae, esli by vremya relaksacii ostavalos' postoyannym.

Dlya ochen' shirokogo diapazona znachenii N₀, ot 30 do 10 000, prodolzhitel'nost' sushestvovaniya rassmatrivaemogo plotnogo izolirovannogo skopleniya okazyvaetsya zaklyuchennoi v ochen' uzkih predelah - ot 44,7 τ₀ do 39,6 τ₀. Odnako takie skopleniya vstrechayutsya tol'ko v voobrazhenii issledovatelei. Opisannyi vyshe process ne uchityvaet nalichiya vokrug yader skoplenii massivnyh protyazhennyh koronal'nyh oblastei, i ego, strogo govorya, mozhno otnesti lish' k yadram skoplenii, kotorye, kak uzhe neodnokratno podcherkivalos' nami, do sravnitel'no nedavnego vremeni polnost'yu otozhdestvlyalis' s samimi skopleniyami. Dostizhenie zvezdoi skorosti otryva ot yadra skopleniya vovse ne oznachaet, chto ona mozhet pokinut' skoplenie. Vyidya iz yadra, ona mozhet zatormozit'sya v korone skopleniya i dazhe vnov' vernut'sya v yadro. Takim obrazom, uskorennyi raspad yadra ne oznachaet uskorennogo raspada skopleniya v celom. Kak pokazal pozzhe tot zhe King (1966a), izmenivshii svoyu tochku zreniya, obshirnaya korona (nazyvaemaya im obolochkoi skopleniya), okruzhayushaya koncentrirovannoe yadro, prepyatstvuet potere zvezd skopleniem. Obshaya skorost' poteri zvezd real'nym skopleniem prakticheski ne zavisit ot stepeni ego koncentracii k centru i opredelyaetsya tol'ko polnym chislom chlenov skopleniya i deistvuyushei na skoplenie prilivnoi siloi, ochen' malo menyayas' s techeniem vremeni.

<< 9.4 Irregulyarnye sily. Maksvellovo raspredelenie skorostei. Teorema viriala. Dinamicheskie massy skoplenii | Oglavlenie | 9.6 Izotermicheskie yadra skoplenii. Opredelenie otnositel'nyh mass zvezd v zvezdnyh skopleniyah >>

Publikacii s klyuchevymi slovami: zvezdy - Skoplenie Publikacii so slovami: zvezdy - Skoplenie
Sm. takzhe: Chernaya dyra razrushaet zvezdu: animaciya Zvezdy, pyl' i tumannost' v NGC 6559 25 samyh yarkih zvezd na nochnom nebe Animaciya: chernaya dyra razrushaet zvezdu Kometa, skopleniya i tumannosti Sravnenie razmerov zvezd Samaya dalekaya iz vseh izvestnyh zvezd? Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce