Astronet > Zvezdnye skopleniya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Zvezdnye skopleniya << 9.5 Vremya relaksacii. Dissipaciya zvezdnyh skoplenii | Oglavlenie | 9.7 Dinamicheskaya evolyuciya zvezdnyh skoplenii >>

9.6 Izotermicheskie yadra skoplenii. Opredelenie otnositel'nyh mass zvezd v zvezdnyh skopleniyah

Pri izuchenii zvezdnyh skoplenii okazyvaetsya udobnym i vozmozhnym pol'zovat'sya nekotorymi terminami i vyvodami teorii stroeniya gazovyh sharov, naprimer, ponyatiem "temperatura". V gazovyh sharah temperatura opredelyaetsya energiei dvizheniya molekul, v zvezdnyh skopleniyah sootvetstvuyushee ponyatie svyazano s energiei dvizheniya zvezd. Rassmotrim maksvellovo raspredelenie skorostei (9.18). V gazovyh sharah rol' parametra j² igraet otnoshenie m/2kT, gde m - massa molekul, T - temperatura, k - postoyannaya Bol'cmana. Esli T postoyanna vo vsem ob'eme shara, to govoryat ob izotermicheskom gazovom share. Po analogii mozhno govorit' ob "izotermicheskom" zvezdnom skoplenii, podrazumevaya pod etim, chto v nem povsyudu gospodstvuet maksvellov zakon raspredeleniya skorostei, prichem parametr j etogo zakona vsyudu odinakov (t. e. dispersiya skorostei zvezd dannoi massy vsyudu odinakova).

V samogravitiruyushei zvezdnoi sisteme potencial F(r) i raspredelenie zvezdnoi plotnosti f(r), otozhdestvlyaemoi v nashem sluchae s plotnost'yu massy, svyazany mezhdu soboi uravneniem Puassona

$\frac{d^2\Phi (r)}{dr^2} + \frac{2}{r}\frac{d\Phi (r)}{dr} + 4\pi Gf(r) = 0.$ (9.37)

Vto zhe vremya v lyubom skoplenii raspredelenie f(r) opredelyaetsya gospodstvuyushim v nem raspredeleniem skorostei ego chlenov. Poetomu izotermicheskoe skoplenie dolzhno imet' sovershenno opredelennoe stroenie, sootvetstvuyushee zakonu

$f(r) = f(0)e^{-2j^2\Phi (r)}.$ (9.38)

Nablyudeniya pokazyvayut, chto ni odno zvezdnoe skoplenie ne yavlyaetsya izotermicheskim vo vsem ego ob'eme, hotya by potomu, chto izotermicheskaya gazovaya sfera imeet beskonechnuyu massu, rastushuyu proporcional'no radiusu sfery. S dostatochnoi stepen'yu tochnosti mozhno prinyat', chto v sostoyanii izotermicheskogo ravnovesiya nahodyatsya central'nye oblasti yader skoplenii, a vo vneshnih chastyah plotnost' padaet bystree, chem esli by oni predstavlyala soboi prodolzhenie central'noi izotermicheskoi sfery. Znaya raspredelenie plotnosti v izotermicheskih yadra skoplenii, mozhno teoreticheski obosnovat' vozmozhnost' opredeleniya otnositel'nyh mass zvezd v zvezdnyh skopleniyah (Herner, 1957). Iz sootnoshenii (9.38) i (9.17) sleduet

$f(r) = f(0)e^{-\frac{3\Phi (r)}{\langle v^2 \rangle}}.$ (9.39)

Pri uslovii vypolneniya zakona ravnoraspredeleniya energii (9.24) dlya zvezd s massami m i m₀ mozhno napisat'

$\left. \begin{array}{l} f(r,m) = f(0,m)\exp[-\frac{3\Phi (r)m}{m_0 \langle v^2(m_0) \rangle}], \\ f(r,m_0) = f(0,m_0)\exp[-\frac{3\Phi (r)}{\langle v^2(m_0) \rangle}]. \end{array} \right\}$ (9.40)

Vvedem oboznacheniya: m/m₀ = μ , g(r, m) = f(r, m)/f(0, m). Togda

$g(r, m) = [g(r, m_0)]^\mu,$ (9.41)

$\lg g(r, m) = \mu\lg g(r, m_0)],$ (9.42)

ili

$\lg f(r, m) = const + \frac{m}{m_0}\lg f(r, m_0).$ (9.43)

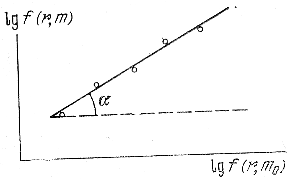
Ris. 142. Diagramma otnositel'nyh koncentracii.

Esli sopostavit' mezhdu soboi velichiny lgf(r, m) i lgf(r, m₀), sootvetstvuyushie odnim i tem zhe znacheniyam r, to mozhno poluchit' tak nazyvaemuyu diagrammu otnositel'nyh mass ili otnositel'nyh koncentracii (ris. 142). Tangens ugla naklona α pryamoi, poluchayusheisya na etoi diagramme, raven μ, t. e. otnosheniyu mass zvezd rassmatrivaemyh grupp. Etot metod opredeleniya otnositel'nyh mass zvezd v zvezdnyh skopleniyah predlozhil i ispol'zoval eshe Ceipel' (1921).

K sozhaleniyu, oshibki v opredelenii ugla naklona pryamoi na ris. 142 ochen' veliki (Holopov, 1955b). Etot naklon ves'ma chuvstvitelen k vyboru centra yadra skopleniya, k uchetu stepeni elliptichnosti yadra. Na ris. 143 (Herner, 1957), pokazana zavisimost' massa - svetimost' ( $\mathfrak M$ , M_{p_v}) dlya zvezd sharovyh skoplenii M 3 i M 92, poluchennaya Hernerom s pomosh'yu ispol'zovaniya diagramm otnositel'nyh koncentracii grupp zvezd raznyh absolyutnyh velichin M_{p_v} v etih skopleniyah. Zdes' massa zvezd $\mathfrak M$ vyrazhena v edinicah massy zvezd s M_{p_v} = 0. Dlya sravneniya pokazana zavisimost' massa - svetimost' dlya zvezd v okrestnostyah Solnca po dannym Salpitera (krivaya a). Herner schitaet, chto hod zavisimosti dlya zvezd skopleniya M 92 neploho soglasuetsya s rezul'tatami, predskazyvaemymi sovremennoi teoriei evolyucii zvezd sharovyh skoplenii (krivaya b). Sootvetstvuyushaya zavisimost' dlya zvezd skopleniya M 3 huzhe soglasuetsya s etoi teoriei, no, uchityvaya bol'shie oshibki opredeleniya otnositel'nyh mass zvezd po metodu Ceipelya, sleduet priznat', chto i v etom sluchae net osnovanii dlya bespokoistva i otnoshenii pravil'nosti upomyanutoi teorii.

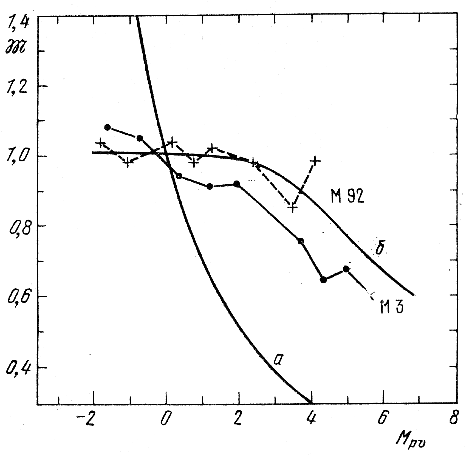
Ris. 143. Zavisimost' massa - svetimost' dlya zvezd sharovyh skoplenii M 3 i M 92 (Herner, 1957); a - zavisimost' massa - svetimost' dlya zvezd v okrestnostyah Solnca, b - sootvetstvuyushaya teorii evolyucii zavisimost' dlya proevolyucionirovavshh zvezd sharovyh skoplenii.

<< 9.5 Vremya relaksacii. Dissipaciya zvezdnyh skoplenii | Oglavlenie | 9.7 Dinamicheskaya evolyuciya zvezdnyh skoplenii >>

Publikacii s klyuchevymi slovami: zvezdy - Skoplenie Publikacii so slovami: zvezdy - Skoplenie
Sm. takzhe: Chernaya dyra razrushaet zvezdu: animaciya Zvezdy, pyl' i tumannost' v NGC 6559 25 samyh yarkih zvezd na nochnom nebe Animaciya: chernaya dyra razrushaet zvezdu Kometa, skopleniya i tumannosti Sravnenie razmerov zvezd Samaya dalekaya iz vseh izvestnyh zvezd? Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

$g(r, m) = [g(r, m_0)]^\mu,$	(9.41)
$\lg g(r, m) = \mu\lg g(r, m_0)],$	(9.42)