Zvezdnye skopleniya << 9.7 Dinamicheskaya evolyuciya zvezdnyh skoplenii | Oglavlenie | 10.1 Funkcii svetimosti zvezd v rasseyannyh skopleniyah >>

---

9.8 Ispol'zovanie EVM dlya resheniya problemy dinamicheskoi evolyucii zvezdnyh skoplenii

Poyavlenie EVM srazu zhe pozvolilo postavit' zadachu proverki vyvodov, poluchennyh statisticheskimi metodami, putem chislennogo integrirovaniya tochnyh uravnenii dvizheniya n tel, ob'edinennyh v samogravitiruyushie sistemy. Tochnost' resheniya pri etom kontroliruetsya trebovaniem postoyanstva obshih integralov dvizheniya. Pri zadanii nachal'nyh koordinat i skorostei chlenov sistemy obychno proveryaetsya vypolnenie teoremy viriala.

Nachalo sistematicheskim issledovaniyam v etom napravlenii bylo polozheno rabotami Hernera (1960; 1963). V pervoi rabote rassmatrivalas' sistema, sostoyashaya iz 16 zvezd, vo vtoroi - iz 25. Nachal'noe raspredelenie plotnosti prinimalos' odnorodnym, raspredelenie skorostei - maksvellovym.

V rezul'tate dinamicheskoi evolyucii sistemy, proslezhennoi vo vtoroi rabote do 40 vremen relaksacii, v nei obrazovalas' central'naya oblast' maksimal'noi plotnosti, soderzhashaya neskol'ko tesnyh par zvezd. Radius sistemy uvelichilsya na tri poryadka, diapazon plotnosti dostig devyati poryadkov. Plotnost' vo vneshnem ob'eme sistemy okazalas' menyayusheisya po zakonu (9.44). Raspredelenie skorostei stalo otlichat'sya ot maksvellova: poyavilsya izbytok bol'shih i malyh skorostei. Pri etom izbytok bol'shih skorostei obuslovlen ne vybrasyvaniem iz sistemy zvezd so skorostyami, prevyshayushimi skorost' otryva (ih chislo okazalos' men'she teoreticheskogo), a poyavleniem v centre skopleniya tesnyh par i grupp zvezd; izbytok malyh skorostei - poyavleniem zvezd, dvizhushihsya bliz apocentrov svoih orbit na bol'shih rasstoyaniyah ot centra skopleniya.

Vyvody Hernera podtverdil Vilen (1967), izuchivshii evolyuciyu treh modelei zvezdnyh skoplenii, harakterizuyushihsya shusterovskim zakonom raspredeleniya plotnosti. Kazhdaya model' sostoyala iz 100 chlenov. Po massam zvezdy delilis' na chetyre gruppy, v sootvetstvii s nachal'noi funkciei svetimosti (sm. § 10.1) sostoyavshie iz chetyreh zvezd s massoi 4,4 solnechnyh, iz 10 zvezd s massoi 2,2, 24 zvezd s massoi 1,1 i 62 zvezd s massoi 0,55 solnechnoi massy. Dve modeli byli stacionarny (odna iz nih byla nadelena differencial'nym vrasheniem).

Okazalos', chto zvezdy, pokidayushie skoplenie so skorostyami otryva, priobretayut etu skorost' ne postepenno (v rezul'tate dalekih sblizhenii), a vnezapno, vsledstvie tesnogo sblizheniya s drugoi zvezdoi ili s nebol'shoi gruppoi zvezd. Etot rezul'tat yavilsya podtverzhdeniem teoreticheskogo vyvoda Enona (1960b) - sm. § 9.5. Procent zvezd, pokidayushih skoplenie, okazalsya pochti ne zavisyashim ot massy zvezdy, ne schitaya togo, chto naibolee massivnye zvezdy voobshe ne pokidayut skoplenie.

Vo vneshnih oblastyah skopleniya i dazhe v oblastyah, blizkih k yadru, ustanavlivaetsya radial'noe pole skorostei. Stendish (1968), a takzhe Arni i Veissman (1973) pokazali, chto ispytyvayushee gravitacionnyi kollaps skoplenie s pervonachal'no odnorodnym raspredeleniem plotnosti i nulevymi nachal'nymi skorostyami ne styagivaetsya v tochku. Po mere priblizheniya k ego centru chlenov, raspolagavshihsya na periferii, bolee blizkie k centru chleny uzhe peresekayut central'nuyu oblast' i nachinayut udalyat'sya ot nee. Minimal'nyi radius skopleniya, dostigaemyi v rezul'tate kollapsa, sostavlyaet 0,2-0,3 velichiny nachal'nogo radiusa kollapsiruyushei sistemy.

Aarset i Hils (1972) rassmotreli dinamicheskuyu evolyuciyu bolee slozhnoi modeli skopleniya, sostoyashei vnachale iz cepochki subskoplenii. Podobnaya struktura nablyudaetsya, v chastnosti, v associacii Oriona. Skoplenie Mech Oriona (sm. frontispis) sostoit iz chetyreh subskoplenii (gruppy HD 37016, gruppy 42 Oriona, skopleniya Trapecii i gruppy i Oriona), raspolozhennyh vdol' pryamoi linii.

Ris. 144 (Aarset, Hils, 1972) pozvolyaet prosledit' za otdel'nymi etapami evolyucii rassmotrennoi imi modeli, kotoruyu mozhno nazvat' model'yu protoskopleniya. Na risunke pokazany polozheniya zvezd protoskopleniya v proekcii na ploskosti XZ i YZ. Pervonachal'naya cepochka subskoplenii raspolozhena vdol' osi Z. Zvezdy pronumerovany v sootvetstvii s ih prinadlezhnost'yu k vos'mi subskopleniyam v nachal'nyi moment vremeni T = 0. Massy ih v kazhdom subskoplenii prinyaty razlichnymi (v sootvetstvii s zakonom massa - svetimost' i nachal'noi funkciei svetimosti zvezd).

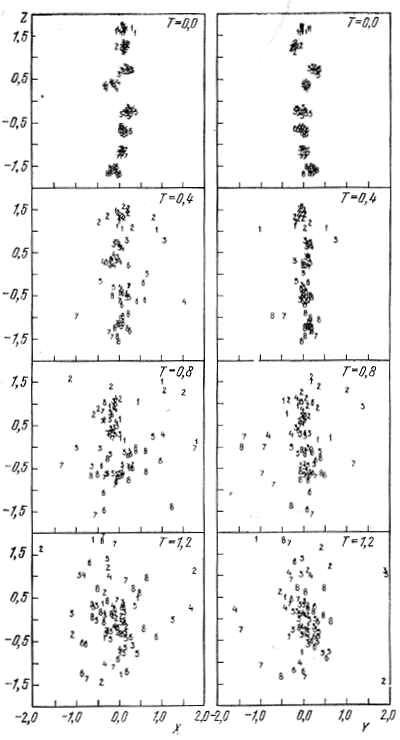
Ris. 144. Dinamicheskaya evolyuciya modeli protoskopleniya sostoyashego iz vos'mi subskoplenii (Aarset, Hils, 1972).

Vnachale subskopleniya pokoyatsya otnositel'no drug druga, zatem nachinaetsya svobodnoe padenie zven'ev cepochki k centru sistemy i vzaimnoe sblizhenie chlenov kazhdogo iz subskoplenii (nachal'nyi kollaps). Vremennoi parametr T na ris. 144 opredelyaetsya vyrazheniem T = t/t₀, gde t - vremya, a t₀ - promezhutok vremeni ot nachala evolyucii skopleniya do momenta maksimal'nogo szhatiya sistemy, obuslovlennogo ee nachal'nym kollapsom. Pri nachal'noi masse protoskopleniya, ravnoi 120 solnechnym massam, i nachal'noi dline cepochki subskoplenii, ravnoi dvum parsekam, t₀ = 3 · 10⁶ let. V processe nachal'nogo kollapsa vosem' subskoplenii slivayutsya i chetyre, zatem v dva i, nakonec, v odno. Odnovremenno iz kazhdogo subskopleniya vybrasyvayutsya zvezdy za schet obrazovaniya vnutri subskoplenii tesnyh dvoinyh sistem.

K momentu sliyaniya vseh subskoplenii v odno (spustya neskol'ko millionov let posle nachala evolyucii) sistema vyglyadit uzhe kak tipichnoe zvezdnoe skoplenie, harakterizuyusheesya nalichiem yadra i okruzhayushei ego stacionarnoi korony, za predelami kotoroi nahodyatsya udalyayushiesya ot skopleniya zvezdy, vybroshennye iz sistemy so skorostyami, prevyshayushimi skorost' otryva. V modeli Aarseta i Hilsa skoplenie teryaet okolo odnoi treti obrazovavshihsya v nem zvezd. Posle dostizheniya dinamicheskogo ravnovesiya (k momentu T = 2 - 2,5) skorost' dinamicheskoi evolyucii skopleniya zametno zamedlyaetsya.

My vidim, chto ispol'zovanie EVM pozvolyaet dopolnit' klassicheskuyu teoriyu dinamicheskoi evolyucii kvazistacionarnyh zvezdnyh skoplenii analizom bystro razvivayushihsya dinamicheskih yavlenii, sootvetstvuyushih pervoi stadii dinamicheskoi evolyucii zvezdnyh sistem po Agekyanu.

V poslednee vremya uvelichivaetsya chislo zvezd v modelyah skoplenii, rassmatrivaemyh raznymi avtorami. Sovershenstvovanie metodiki vychislenii pozvolyaet dovesti eto chislo do 500 (Vilen, 1974; Aarset, 1973; 1974). Poyavlyayutsya takzhe raboty, v kotoryh uchityvaetsya poterya massy chlenami skoplenii, obuslovlennaya ih fizicheskoi evolyuciei kak na rannei (protozvezdnoi), tak i na bolee pozdnih stadiyah razvitiya.

Odnako do sih por ne yasno, do kakih predelov mozhno ekstrapolirovat' rezul'taty, poluchennye dlya modelei, soderzhashih nebol'shoe chislo chlenov (N < 500), na real'nye sharovye skopleniya, sostoyashie iz desyatkov i soten tysyach zvezd.

---

<< 9.7 Dinamicheskaya evolyuciya zvezdnyh skoplenii | Oglavlenie | 10.1 Funkcii svetimosti zvezd v rasseyannyh skopleniyah >>

Publikacii s klyuchevymi slovami: zvezdy - Skoplenie Publikacii so slovami: zvezdy - Skoplenie
Sm. takzhe: Chernaya dyra razrushaet zvezdu: animaciya Zvezdy, pyl' i tumannost' v NGC 6559 25 samyh yarkih zvezd na nochnom nebe Animaciya: chernaya dyra razrushaet zvezdu Kometa, skopleniya i tumannosti Sravnenie razmerov zvezd Samaya dalekaya iz vseh izvestnyh zvezd? Vse publikacii na tu zhe temu >>