Astronet > Razmernosti i podobie astrofizicheskih velichin

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 1.1 Razmernosti astrofizicheskih velichin | Oglavlenie | § 1.3 Podobie i modelirovanie >>

§ 1.2 Astrofizicheskie formuly i P-teorema

Odna iz osnovnyh zadach astrofiziki - nahozhdenie sootnoshenii, svyazyvayushih mezhdu soboi parametry nebesnyh tel. Pust', naprimer, zvezda imeet nekotoruyu opredelennuyu massu. Kakova ee svetimost'? Mozhet li eta velichina byt' proizvol'noi, ili ona imeet odno ili neskol'ko opredelennyh znachenii? Razlichayutsya li svetimosti zvezd s odnoi massoi, no s raznymi radiusami i t. d.? Kak pravilo, v astrofizike podobnye zavisimosti imeyut statisticheskii harakter. Skazhem, esli schitat', chto svetimost' zvezdy dannogo tipa odnoznachno opredelyaetsya massoi, to na samom dele imeetsya nekotoryi razbros svetimostei okolo srednego znacheniya. Pravda, otchasti etot razbros svyazan s neizbezhnymi oshibkami nablyudenii kak v opredelenii svetimosti, tak i v opredelenii massy. No otchasti on i vpolne realen, poskol'ku raznye zvezdy odnogo i togo zhe tipa mogut hotya by nemnogo razlichat'sya himicheskim sostavom, vrasheniem, magnitnym polem. Razumeetsya, pri teoreticheskom vyvode sootnoshenii eti razlichiya, v principe, mogut byt' uchteny.

Astrofizicheskie sootnosheniya mogut byt' polucheny iz nablyudenii, esli sobran dostatochno bol'shoi statisticheskii material, i iz teorii, esli my dostatochno horosho ponimaem fizicheskie processy, lezhashie v osnove togo ili inogo yavleniya. Pravda, chashe vsego i nablyudenii nedostatochno, i fizika yavleniya chastichno ostaetsya neyasnoi. Nablyudatel'nye dannye obychno predstavlyayut v forme grafikov ili tablic. Krivye na grafikah ili tablichnye dannye mozhno opisat' s pomosh'yu approksimacionnyh, ili, kak ih chasto nazyvayut, empiricheskih formul. Naprimer, zavisimost' spektral'nogo potoka izlucheniya F_ν ot chastoty dlya mnogih ob'ektov mozhet byt' approksimirovana stepennoi formuloi

$F_\nu \sim \nu^{-\alpha}$ (1.5)

v opredelennom intervale chastot. Zdes' spektral'nyi indeks α - velichina, podbiraemaya tak, chtoby krivaya (1.5) nailuchshim obrazom sootvetstvovala by nablyudeniyam izlucheniya dannogo ob'ekta v opredelennom intervale chastot. Kak pravilo, empiricheskie formuly ne universal'ny v tom smysle, chto oni primenimy lish' k opredelennym intervalam uslovii. Naprimer, sootnoshenie (1.5) mozhet byt' spravedlivo v radiodiapazone i ne goditsya dlya opisaniya opticheskogo izlucheniya; ono mozhet byt' ispol'zovano dlya raznyh diapazonov izlucheniya odnogo ob'ekta, no pri otdel'nom podbore parametra α dlya kazhdogo diapazona.

Chasto okazyvaetsya, chto naidennaya vnachale empiricheskaya formula okazyvaetsya zatem neprigodnoi po mere togo, kak nakaplivayutsya i utochnyayutsya nablyudatel'nye dannye. No nesmotrya na vse eti nedostatki, opredelenie empiricheskih zavisimostei igraet ogromnuyu rol' v astrofizike, pozvolyaya v szhatom vide opisat' dannye nablyudenii, pokazyvaya napravlenie dal'neishego poiska zavisimostei, davaya vozmozhnost' bolee tochnoi fizicheskoi interpretacii yavlenii i bolee nadezhnogo sopostavleniya teorii i nablyudenii. Zametim, chto, kak pravilo, empiricheskie formuly predstavlyayut soboi prostye algebraicheskie (stepennye) sootnosheniya.

V rezul'tate teoreticheskogo analiza my tozhe poluchaem formuly, opisyvayushie svyazi mezhdu raznymi astrofizicheskimi parametrami. Sopostavlenie teoreticheskih i empiricheskih zavisimostei sluzhit osnovnym metodom proverki pravil'nosti nashego ponimaniya fiziki yavleniya. Teoreticheskie formuly, razumeetsya, mnogo slozhnee empiricheskih, poskol'ku zdes' prihoditsya uchityvat' mnogo razlichnyh, bolee ili menee proizvol'no zadavaemyh faktorov i uslovii. No i zdes' my chasto staraemsya uprostit' formuly, privesti ih k naibolee udobnomu vidu algebraicheskih stepennyh zavisimostei.

Nakonec ochen' chasto byvaet i tak, chto intuitivno chuvstvuetsya neobhodimost' zavisimosti mezhdu parametrami nebesnyh tel, - no ni teoriya, ni nablyudeniya poka etoi zavisimosti, dazhe v ee prosteishei forme, vyyavit' ne mogut. I zdes' estestvenno voznikaet vopros - mozhno li s pomosh'yu analiza razmernostei izuchit' approksimacnonnye empiricheskie formuly i poluchit' teoreticheskie zavisimosti?

V samom dele, soobrazheniya razmernosti pozvolyayut poluchit' sootnosheniya mezhdu parametrami na osnove lish' ochen' obshih predstavlenii o fizicheskih svoistvah nebesnyh tel i togda, kogda detal'naya kartina processov ostaetsya ne yasnoi. Chasto odnoi intuicii dostatochno, chtoby naiti iz soobrazhenii razmernosti nuzhnoe nam sootnoshenie. No i v teh sluchayah, kogda my mozhem poluchit' teoreticheskim putem te ili inye formuly, soobrazheniya razmernosti pozvolyayut luchshe ponyat' ih smysl, otbrosit' vtorostepennye faktory i znachitel'no ih uprostit'. Znaya empiricheskie formuly (kotorye obychno ne uchityvayut razmernostnyh soobrazhenii), mozhno iz uslovii razmernosti poluchit' bolee tochnye formuly.

Vo mnogih sluchayah sootnosheniya, poluchennye na osnove soobrazhenii razmernosti, nichut' ne huzhe "tochnoi" teorii. Naprimer, dlya teoreticheskogo analiza chasto prihoditsya uchityvat' geometricheskie faktory, kotorye, kak pravilo, ostayutsya neopredelennymi. V ramkah analiza razmernostei my obychno otvlekaemsya ot etih faktorov, ostavlyaya lish' te fizicheskie parametry, kotorye deistvitel'no opredelyayut sut' yavleniya i vmeste s tem mogut byt' dostatochno, nadezhno sravneny s nablyudeniyami.

My nadeemsya, chto vse posleduyushee izlozhenie i rassmotrenie konkretnyh problem pozvolit chitatelyu yasno ponyat' dostoinstva i nedostatki metoda analiza razmernostei v specificheskih astrofizicheskih usloviyah.

Primenenie metoda analiza razmernostei osnovano na principe razmernoi odnorodnosti, matematicheskim vyrazheniem kotorogo yavlyaetsya P-teorema (inogda, osobenno v literature na angliiskom yazyke, nazyvaemaya takzhe teoremoi Bekingema). Princip razmernoi odnorodnosti byl sformulirovan eshe Fur'e, a pervye sistematicheskie primeneniya metoda analiza razmernostei byli dany Releem. Veroyatno, kazhdomu chitatelyu princip razmernoi odnorodnosti v ego prosteishei forme uzhe izvesten: vse uravneniya, opisyvayushie lyubye fizicheskie yavleniya, imeyut takuyu formu, chto vhodyashie v nih slagaemye obladayut odinakovoi razmernost'yu, a argumenty transcendentnyh funkcii (trigonometricheskih, logarifmichechesknh i t. p.) bezrazmerny.

Skazannoe otnositsya imenno k fizicheskim uravneniyam. Empiricheskie formuly chasto zapisyvayutsya bez soblyudeniya principa razmernoi odnorodnosti p poetomu oni spravedlivy tol'ko pri opredelennom masshtabe izmereniya parametrov. Princip razmernoi odnorodnosti srazu sleduet iz trebovaniya, chtoby vse fizicheskie zakony i opisyvayushie ih uravneniya ne zaviseli by ot vybora masshtaba edinic izmereniya.

Strogie matematicheskie dokazatel'stva principa razmernoi odnorodnosti i P-teoremy dany v knigah po metodu analiza razmernostei i podobiya. My ne budem zdes' podrobno zanimat'sya etoi matematicheskoi teoriei. Chitatel' smozhet poznakomit'sya s etimi voprosami po upomyanutoi v predislovii knige L. I. Sedova "Metody podobiya i razmernosti v mehanike" [2] i po ryadu drugih monografii (sm. [3-7]).

Formulirovku P-teoremy my poyasnim na osnove astrofizicheskih primerov. Metod ee primeneniya po sushestvu i est' metod ee dokazatel'stva. Nado, pravda, zametit', chto hotya v teorii analiza razmernostei i sushestvuyut nekotorye formal'nye pravila, vse zhe vo mnogih sluchayah bol'shuyu rol' igraet intuiciya, neobhodimost' dogadyvat'sya, kak luchshe postupit' v tom pli inom konkretnom sluchae.

Rassmatrivaya kakie-libo svoistva nebesnogo tela ili astrofizicheskogo yavleniya, my prezhde vsego dolzhny vyyasnit', kakie parametry ego harakterizuyut. Budem nazyvat' takie parametry opredelyayushimi. Nekotorye iz nih nahodyatsya po dannym nablyudenii (massa, razmery, svetimost' i t. d.), drugie zadayutsya na osnovanii nashih predstavlenii o fizike yavlenii (naprimer, himicheskii sostav, koefficient poglosheniya, nalichie bystryh chastic, magnitnyh polei i t. p.), tret'i yavlyayutsya universal'nymi konstantami, opredelyaemymi obshimi fizicheskimi zakonami, opisyvayushimi sostoyanie i processy v dannom ob'ekte (postoyannaya tyagoteniya N'yutona, skorost' sveta, postoyannaya zakona Stefana - Bol'cmana i dr.).

Razumeetsya, vazhnost' i neobhodimost' zadaniya raznyh opredelyayushih parametrov v kazhdom konkretnom sluchae ves'ma razlichna. Kakie i skol'ko opredelyayushih parametrov nado vybrat', chtoby adekvatnym obrazom oharakterizovat' interesuyushee nas yavlenie, obychno prihoditsya reshat' na osnove opyta pli fizicheskoi intuicii. Razumeetsya, esli my imeem dostatochno polnuyu teoriyu rassmatrivaemogo yavleniya, t. e. mozhem napisat' opisyvayushuyu eto yavlenie sistemu uravnenii, to eta sistema srazu zhe daet nam i ves' nabor opredelyayushih parametrov.

V astrofizike est' mnogo zadach, gde udaetsya napisat' sravnitel'no polnye sistemy uravnenii, poluchit' ih resheniya i podrobnym obrazom issledovat' ih. Bol'shogo sovershenstva dostigla teoriya vnutrennego stroeniya zvezd, teoriya rasprostraneniya elektromagnitnyh voln v kosmicheskoi plazme, teoriya udarnyh voln. No i zdes' okazyvaetsya poleznym metod podobiya i razmernostei. V chastnosti, k teorii vnutrennego stroeniya zvezd i k zadache o rasprostranenii udarnyh voln v zvezdah vpervye metod podobiya byl primenen L. I. Sedovym eshe v 1954 g. (izlozhenie sm. v [2]).

V nastoyashei knige my budem takzhe zanimat'sya temi naibolee chasto vstrechayushimisya v astrofizike sluchayami, kogda polnoi sistemy uravnenii napisat' voobshe nel'zya, libo ona okazyvaetsya slishkom gromozdkoi. Poetomu v podobnyh zadachah pri vybore opredelyayushih parametrov prihoditsya opirat'sya na intuitivnye predstavleniya o fizike yavleniya.

Vprochem, primenenie metoda analiza razmernostei sushestvenno i v teh sluchayah, kogda imeetsya bolee polnaya teoriya. Chasto v astrofizike predstavlenie o tom, chto sostavlennaya nami sistema uravnenii pravil'no opisyvaet yavlenie, okazyvaetsya obmanchivym, poskol'ku net uverennosti, chto uchteno vse, chto nuzhno. Matematicheskaya tochnost' rascheta pri reshenii takih uravnenii okazyvaetsya illyuzornoi i mozhet vvesti v zabluzhdenie, naprimer, neiskushennogo v teorii nablyudatelya. Prostye razmernostnye sootnosheniya, chetko opredelyayushie, chto uchteno i chto net, i imeyushie ochen' prozrachnyi vid, dayut yasnoe fizicheskoe predstavlenie ob interesuyushem nas yavlenii. Mnogo primerov my privedem v posleduyushih glavah.

Vernemsya k P-teoreme. Pust' u nas est' nekotoryi nabor p opredelyayushih parametrov A₁, A₂, ..., A_n s razmernostyami, oboznachaemymi, kak obychno, [A₁], [A₂],...,[A_n]. Nekotorye iz etih velichin mogut imet' i odinakovye razmernosti, hotya sami velichiny libo sil'no otlichayutsya po velichine, libo voobshe opisyvayut fizicheski raznye parametry (naprimer, skorost' chastic gaza i al'venovskaya skorost').

Iz vsego nabora opredelyayushih parametrov mozhno vydelit' velichiny s nezavisimymi razmernostyami, t. e. takie, chto razmernost' kazhdoi iz nih ne mozhet byt' predstavlena v vide kombinacii razmernostei drugih vydelennyh parametrov. Drugoe opredelenie velichin s nezavisimymi razmernostyami: iz nih nel'zya postroit' bezrazmernogo kompleksa. Ochevidnyi astrofizicheskii primer: massa [M] = g, razmer [R] = sm i svetimost' [L] = $\frac{\mbox{g} \cdot \mbox{sm}^2}{\mbox{sek}^3}$ . Srazu vidno, chto iz M, R i L nel'zya postroit' bezrazmernogo kompleksa. Chislo parametrov s nezavisimymi razmernostyami ne mozhet byt' bol'she chisla osnovnyh, pervichnyh edinic izmereniya, no mozhet byt' i men'she. My uslovilis' v astrofizike pol'zovat'sya chetyr'mya osnovnymi edinicami - dliny, massy, vremeni i temperatury, poetomu chislo parametrov s nezavisimymi razmernostyami ne bol'she chetyreh. No etih parametrov mozhet byt' i men'she, i my chasto budem vstrechat'sya s takim naborom parametrov, iz kotoryh tol'ko tri ili dazhe dva yavlyayutsya nezavisimymi po razmernosti. V dal'neishem v perechislenii opredelyayushih parametrov nezavisimye po razmernosti velichiny budem pomeshat' v nachale spiska.

Teper' dopustim, chto my ishem kakoe-libo sootnoshenie, svyazyvayushee te ili inye parametry izuchaemogo nebesnogo ob'ekta. Pust' etot ob'ekt harakterizuetsya naborom n opredelyayushih parametrov. Zapishem iskomoe sootnoshenie - formulu, svyazyvayushuyu mezhdu soboi opredelyayushie parametry, v sleduyushem obshem vide:

$f(A_1, A_2, ..., A_n) = 0.$ (1.6)

Nahozhdenie yavnogo vida etih sootnoshenii i est' osnovnaya zadacha astrofiziki (kak i lyuboi drugoi nauki).

Izvestnaya P-teorema utverzhdaet, chto sootnoshenie (1.6) mozhet byt' perepisano v vide

$f(\underbrace{1,1,...,1}_{k}; \quad \underbrace{\Pi_{k+1},\Pi_{k+2},...,\Pi_n}_{n-k})=0,$ (1.7)

gde cherez k oboznacheno chislo opredelyayushih parametrov s nezavisimymi razmernostyami, a cherez P oboznacheny bezrazmernye .kombinacii (v dal'neishem my ih budem nazyvat' kompleksami) vseh velichin A₁, A₂, ..., A_n. Vybor bezrazmernyh kompleksov P_k+1, P_k+2, ..., P_n dolzhen byt' podchinen opredelennym pravilam, hotya on i ne yavlyaetsya odnoznachnym. Naprimer, nado stremit'sya k tomu, chtoby kak mozhno bol'shee chislo etih kompleksov byli by nezavisimymi, t. e. ne mogli by byt' svedeny odin k drugomu putem vozvedeniya v stepen' ili peremnozheniya. Takim obrazom, sushnost' P-teoremy zaklyuchaetsya v tom, chto on svodit funkciyu n razmernyh parametrov k funkcii men'shego chisla n - k bezrazmernyh kompleksov. Strogoe dokazatel'stvo i predely primenimosti P-teoremy privedeny, naprimer, v [2, 3], a takzhe i v drugih rukovodstvah po primeneniyu metoda analiza razmernostei [4-7].

Metod dokazatel'stva osnovan na principe razmernoi odnorodnosti - sootnoshenie (1.6) ne dolzhno izmenit'sya, esli my izmenim sistemu edinic. Poetomu my mozhem umnozhit' vse razmernostnye argumenty funkcii (1.6) na odin i tot zhe mnozhitel' bez narusheniya etogo uravneniya. Vybiraya etot mnozhitel' ravnym 1/A₁ poluchim pervuyu edinicu v (1.7). Poskol'ku chislo mnozhitelei s nezavisimymi razmernostyami ravno k, to takuyu proceduru mozhno prodelyvat' k raz, v rezul'tate chego ostanetsya v uravnenii k edinic i n - k bezrazmernyh kompleksov.

Razumeetsya, vid funkcii (1.7) tot zhe, chto iv (1.6), metodom teorii razmernostei on ne opredelyaetsya. Analiz razmernostei imeet delo tol'ko s argumentami etih funkcii. Tem ne menee uzhe iz obshego sravneniya (1.6) i (1.7) mozhno sdelat' ryad vazhnyh vyvodov.

Vo-pervyh, sleduet podcherknut', chto umen'shenie chisla argumentov (ot n v (1.6) do n - k v (1.7)) predstavlyaet soboi sushestvennoe uproshenie sootnosheniya. Po obraznomu vyrazheniyu Klaina [4], funkciya odnogo argumenta mozhet byt' tabulirovana v odnoi strochke, funkciya dvuh argumentov - na stranice, tablica funkcii treh argumentov trebuet knigi, a chetyreh - biblioteki.

Vo vtoryh, esli n - k=1, t. e. esli chislo opredelyayushih parametrov vsego na edinicu bol'she chisla parametrov s nezavisimoi razmernost'yu, to vmesto (1.7) imeem

$f(1, 1, ..., 1; \Pi) = f_1(\Pi) = 0.$ (1.8)

Zdes' ostaetsya odin bezrazmernyi kompleks. Formula (1.8) teper' imeet vid uravneniya tol'ko dlya odnoi velichiny, reshenie kotorogo opredelyaet chislennoe znachenie (odno ili neskol'ko) velichiny P. Chasto uravnenie (1.8) imeet prostuyu algebraicheskuyu formu i ego koren', kak pravilo, okazyvaetsya po poryadku velichiny ne slishkom sil'no otlichayushimsya ot edinicy.

Takim obrazom, v tom vazhnom sluchae, kogda chislo opredelyayushih parametrov na edinicu bol'she chisla nezavisimyh razmernostei, sovershenno ne znaya zaranee vida funkcii, svyazyvayushei eti parametry, iz odnih tol'ko razmernostnyh soobrazhenii my mozhem opredelit' etu funkciyu s tochnost'yu do chislennogo mnozhitelya, kotoryi chasto sravnim s edinicei. Dlya bolee tochnogo opredeleniya chislennogo mnozhitelya mozhno ispol'zovat' nablyudatel'nye dannye ili metod modelirovaniya.

V-tret'ih, vo mnogih sluchayah dazhe pri bol'shem chisle opredelyayushih parametrov, t. e. pri n - k > 1, mozhno poluchit' iskomye zavisimosti. Rassmotrim sluchai, kogda v (1.7) vse bezrazmernye kompleksy P_k+2, ..., P_n, krome P_k+1, maly po sravneniyu s edinicei. Togda mozhno napisat':

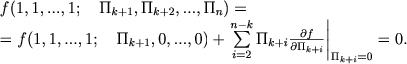
$\begin{array}{l} f(1,1,...,1; \quad \Pi_{k+1},\Pi_{k+2},...,\Pi_n)= \\ = f(1,1,...,1; \quad \Pi_{k+1},0,...,0)+\left.\sum\limits^{n-k}_{i=2} \Pi_{k+i}\frac{\partial f}{\partial \Pi_{k+i}}\right|_{\Pi_{k+i}=0} = 0. \end{array}$ (1.9)

V pervom priblizhenii, pri P_k+1 << 1 otsyuda opyat' sleduet sootnoshenie f(1, 1,..., 1; P_k+1, 0, ..., 0) = 0, kotoroe odnoznachno opredelyaet chislennoe znachenie edinstvennogo "znachashego" bezrazmernogo kompleksa. Inymi slovami, esli my mozhem tak skonstruirovat' polnyi nabor (t. e. vseh n - k) bezrazmernyh kompleksov, chto tol'ko odin iz nih ne mal po sravneniyu s edinicei, to otsyuda tozhe mozhno poluchit' zavisimost' mezhdu opredelyayushimi parametrami s tochnost'yu do postoyannogo mnozhitelya poryadka edinicy. To zhe samoe imeet mesto, esli kakie-libo iz kompleksov P_k+2, ..., P_n mnogo bol'she edinicy. Togda v (1.9) mozhno ispol'zovat' sootvetstvuyushee razlozhenie po velichinam $\Pi_{k+1}^{-1}$ . Takim obrazom, esli iz vsego nabora bezrazmernyh kompleksov imeetsya tol'ko odin "znachashii" kompleks, velichina kotorogo ne slishkom sil'no otlichaetsya ot edinicy v obe storony, a vse ostal'nye kompleksy libo mnogo men'she edinicy, libo mnogo bol'she, to etot znachashii kompleks dolzhen byt' konstantoi, chislennoe znachenie kotoroi opredelyaetsya v teorii odnoznachno.

I, nakonec, v samom obshem sluchae, kogda est' neskol'ko sravnimyh po velichine bezrazmernyh kompleksov, iz razmernostnyh soobrazhenii mozhno vse zhe poluchit' iskomye sootnosheniya. Odnako teper' vmesto postoyannyh koefficientov poyavlyayutsya menyayushiesya velichiny, izmenenie kotoryh, vprochem, chasto ogranicheno nekotorymi predelami.

<< § 1.1 Razmernosti astrofizicheskih velichin | Oglavlenie | § 1.3 Podobie i modelirovanie >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce