Astronet > Razmernosti i podobie astrofizicheskih velichin

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 1.3 Podobie i modelirovanie | Oglavlenie | § 1.5 Mirovye (fundamental'nye) postoyannye >>

§ 1.4 Primery primeneniya analiza razmernostei k astrofizicheskim zadacham

Obshii metod postroeniya bezrazmernyh kompleksov i opredeleniya zavisimostei mezhdu razlichnymi velichinami proshe vsego srazu proillyustrirovat' na konkretnyh primerah. I delo ne tol'ko v tom, chto takie primery v silu svoei naglyadnosti pozvolyayut yasnee ponyat' sushnost' metoda. Ochen' vazhno takzhe i to, chto v metodah primeneniya teorii razmernostei bol'shuyu rol' igraet intuiciya i poetomu zdes' ne vsegda mozhno deistvovat' v ramkah formal'nyh pravil. Razumeetsya, formal'noe primenenie metoda teorii razmernostei vsegda daet pravil'nye rezul'taty, no ne vsegda imenno to, chto nas interesuet.

Matematicheskaya storona primeneniya metoda razmernostei k konkretnym zadacham obychno svoditsya k resheniyu ochen' elementarnoi algebraicheskoi sistemy uravnenii. Udobno dlya zapisi etih uravnenii vvesti matrichnoe oboznachenie, predlozhennoe Langhaarom (sm. [5]). V dal'neishem my budem chasto privodit' eti matricy razmernosti v raznyh zadachah.

Izlozhenie teorii razmernostei chasto nachinayut s opisaniya resheniya zadachi o kolebanii mayatnika. S podobnoi astrofizicheskoi zadachi - problemy pul'sacii zvezd - nachnem i my. V prosteishem sluchae lineinogo mayatnika prenebregaetsya amplitudoi kolebanii, schitaetsya, chto ona mala. My tozhe budem schitat' amplitudu pul'sacii zvezd maloi, t. e. rassmotrim lineinye pul'sacii.

Kak izvestno, pul'sacii zvezd predstavlyayut soboi periodicheskie szhatiya i rasshireniya zvezd, po-vidimomu, imeyushie dovol'no strogo vyrazhennyi radial'nyi harakter. Kak pokazyvayut nablyudeniya, amplituda kolebanii ne bolee 5%, tak chto pul'sacii mozhno deistvitel'no schitat' lineinymi. Odnako sami kolebaniya nesinusoidal'ny, vremya rasshireniya i vremya szhatiya neodinakovy. Strogo govorya, lineinye kolebaniya dolzhny byt' sinusoidal'ny, no nablyudaemye otkloneniya ot etoi simmetrii mogut byt' ob'yasneny yavleniyami v poverhnostnyh sloyah pul'siruyushih zvezd, gde otnositel'naya amplituda kolebanii ne mala. Eto privodit k otnositel'nomu smesheniyu fazy kolebanii na raznyh glubinah i k iskazheniyu profilya kolebanii. Kak pokazyvayut raschety, kolebaniya v glubokih sloyah pul'siruyushih zvezd imeyut bolee sinusoidal'nyi harakter, i lineinoe priblizhenie okazyvaetsya vpolne dostatochnym, po krainei mere v pervom priblizhenii, kotorym my v etom paragrafe i ogranichimsya. Bolee tonkie effekty budut obsuzhdeny v gl. 5.

Zdes' my rassmotrim prosteishuyu problemu teorii pul'sacii zvezd: opredelenie perioda kolebanii v pervom priblizhenii. V ramkah metoda analiza razmernostei budem ishodit' iz nabora treh osnovnyh parametrov zvezd: massy M, svetimosti L i radiusa R. Krome togo, ochevidno, chto sami pul'sacii tesno svyazany s yavleniem vsemirnogo tyagoteniya, harakterizuemym postoyannoi N'yutona G - ved' szhatie zvezdy pri pul'sacii vyzvano polem tyagoteniya zvezdy. Nakonec, v lineinom priblizhenii pul'sacii harakterizuyutsya tol'ko chastotoi ili periodom R. Takim obrazom, imeem pyat' osnovnyh, opredelyayushih parametrov: M, L, R, G, R s razmernostyami:

$[M] = \mbox{g}, \, [L] = \frac{\mbox{g} \cdot \mbox{sm}^2}{\mbox{sek}^3}, \, [R] = \mbox{sm}, \, [G] = \frac{\mbox{sm}^3}{\mbox{g} \cdot \mbox{sek}^2}, \, [P] = \mbox{sek}.$ (1.10)

Dostatochno li etih parametrov? Dlya polnoi teorii pul'sacii zvezd etogo, konechno, nedostatochno - izvestno, chto odni zvezdy s odnim i tem zhe naborom parametrov M, L, R ne pul'siruyut, a drugie pul'siruyut. Kak bylo pokazano, naprimer, S. A. Zhevakinym eshe v 1953 g., zvezda s podhodyashim naborom parametrov M, L, R budet pul'sirovat' tol'ko togda, kogda soderzhanie geliya v nei ne menee 15%, i kogda koefficient neprozrachnosti veshestva takoi, chto vozmozhno deistvie "klapannogo" mehanizma, kompensiruyushego poteri energii pri dissipacii dvizhenii pul'sacii. Ochevidno, chto pul'sacii zvezd, a vozmozhno, i tochnoe znachenie perioda, zavisyat ot struktury zvezdy i ot ee himicheskogo sostava. No, eshe raz podcherkivaem, zadacha teorii razmernostei zaklyuchaetsya ne v tom, chtoby dat' otvet na vopros, kakova priroda yavleniya, a v tom, chtoby, ishodya tol'ko iz razmernostei velichin, poluchit' ocenki parametrov v predpolozhenii, chto samo yavlenie imeet mesto.

Parametry (1.10) yavlyayutsya osnovnymi i oni dolzhny opredelit' period pul'sacii zvezd - esli eti pul'sacii deistvitel'no imeyut mesto. Drugie parametry, v tom chisle i ochen' vazhnye dlya vozniknoveniya pul'sacii (himicheskii sostav, koefficient neprozrachnosti, rol' ionizacii v poverhnostnyh sloyah, konvekciya i t. p.), estestvenno, v kakoi-to stepeni vliyayut na velichinu perioda, no uzhe v sleduyushem priblizhenii.

Zapishem v neyavnom vide neizvestnuyu nam formulu, svyazyvayushuyu parametry (1.10):

$f(M, L, R, G, R)=0.$ (1.11)

Chislo nezavisimyh razmernostei ravno trem. Sledovatel'no, soglasno P-teoreme est' dva bezrazmernyh kompleksa, P₁ i P₂, i my mozhem sootnoshenie (1.11) perepisat' v vide:

$f(\Pi_1, \, \Pi_2)=0.$ (1.12)

Dlya nahozhdeniya bezrazmernyh kompleksov P₁ i P₂ sostavim matricu razmernosti:

$\begin{matrix} \, & [M] & [L] & [R] & [G] & [P] \\ \mbox{g}&1&1&0&-1&0 \\ \mbox{sm}&0&2&1&3&0 \\ \mbox{sek}&0&-3&0&-2&1 \end{matrix}$ (1.13)

Komponenty (matrichnye elementy) matricy razmernosti est' pokazateli stepenei, v kotoryh edinicy razmernostei (perechislennye sleva) vhodyat v opredelyayushie parametry (perechislennye sverhu). Chislo stolbcov ravno chislu opredelyayushih parametrov, chislo strok ravno chislu pervichnyh osnovnyh edinic izmereniya.

Vsyakaya matrica, v tom chisle i matrica razmernosti, harakterizuetsya ee rangom, t. e. rangom naibol'shego po chislu strok i stolbcov nenulevogo determinanta. V sluchae (1.13) otlichen ot nulya determinant tret'ego ranga, sostavlennyi, naprimer, iz treh pervyh stolbcov (ili treh poslednih, eto vse ravno). Sledovatel'no, i rang matricy razmernosti zdes' raven trem. Legko videt', chto vsegda rang matricy razmernosti raven chislu opredelyayushih parametrov s nezavisimymi razmernostyami v polnom nabore opredelyayushih parametrov. Rang matricy razmernosti ne bol'she chisla strok, no mozhet byt' i men'she. Kak pravilo, etot sluchai mozhno zaranee predusmotret' i ne vypisyvat' lishnih strok.

V sootvetstvii s opredeleniem formuly razmernosti (stepennyh zavisimostei (1.1)) lyuboi bezrazmernyi kompleks v nashei zadache mozhet byt' zapisan v vide

$\Pi = M^{k_1}L^{k_2}R^{k_3}G^{k_4}P^{k_5},$ (1.14)

gde k₁, k₂, k₃, k₄, k₅ est' iskomye pokazateli stepeni. Ispol'zuya matricu razmernosti, legko sostavit' algebraicheskuyu sistemu uravnenii dlya opredeleniya etih pokazatelei:

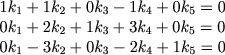
$\begin{array}{l} 1k_1 + 1k_2 + 0k_3 - 1k_4 + 0k_5 = 0\\ 0k_1 + 2k_2 + 1k_3 + 3k_4 + 0k_5 = 0 \\ 0k_1 - 3k_2 + 0k_3 - 2k_4 + 1k_5 = 0 \end{array}$ (1.15)

Poluchilas' sistema iz treh uravnenii dlya opredeleniya pyati neizvestnyh velichin. Poskol'ku rang matricy raven trem, to otsyuda sleduet, chto dva iz iskomyh pyati pokazatelei mozhno zadavat' proizvol'no. Togda ostal'nye velichiny k_i poluchayutsya putem resheniya sistemy (1.15). Vprochem, nado imet' v vidu, chto hotya vybor dvuh znachenii parametrov k_i i proizvolen, no pri etom sleduet vse zhe rukovodstvovat'sya nekotorymi intuitivnymi fizicheskimi soobrazheniyami dlya togo, chtoby potom bezrazmernym kompleksam mozhno bylo by pripisat' fizicheskii smysl, pozvolyayushii poluchit' ih naglyadnuyu interpretaciyu.

Dlya pervogo kompleksa, kotoryi i dolzhen opredelyat' period, vyberem pokazatel' pri R, t. e. k₅, ravnym edinice.

Teper' mozhno proizvol'no vybrat' odin iz ostal'nyh pokazatelei k₁, k₂, k₃ ili k₄ ravnym nulyu. Luchshe vsego sdelat' tak, chtoby isklyuchit' odin iz osnovnyh parametrov zvezdy M, L ili R. Poskol'ku kolebaniya mehanicheskie, to kazhetsya bolee vazhnoi zavisimost' ot M i R Primem poetomu k₂ = 0. Togda reshenie sistemy (1.15) nahoditsya bez truda i my imeem k₁ = k₄ = 1/2, k₃ = -3/2. Eto i daet nam pervyi bezrazmernyi kompleks:

$PC^{1/2}M^{1/2}R^{-3/2} = \Pi_1.$ (1.16)

Zdes' mozhno otdelit' astrofizicheskie izmeryaemye velichiny ot universal'nyh postoyannyh i, krome togo, vospol'zovat'sya opredeleniem srednei plotnosti zvezdy $\bar\rho = 3M/4\pi R^3$ . Togda poluchim

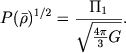
$P(\bar\rho)^{1/2} = \frac{\Pi_1}{\sqrt{\frac{4\pi}{3}G}}.$ (1.17)

Eto est' horosho izvestnoe v astrofizike sootnoshenie "period - plotnost'" dlya pul'siruyushih zvezd, esli schitat' pravuyu chast' postoyannoi velichinoi. Ispol'zuya nablyudatel'nye dannye, mozhno priblizhenno napisat'

$P(\bar\rho)^{1/2} = 0^d,026\frac{\mbox{g}^{1/2}}{\mbox{sm}^{3/2}}.$ (1.18)

Smysl bezrazmernogo kompleksa (1.16) - (1.18) legko ponyat', ispol'zuya analogiyu s kolebaniyami mayatnika. Kak izvestno iz formuly Gyuigensa, period kolebanii matematicheskogo mayatnika dlinoi l v pole tyazhesti s uskoreniem g raven

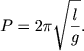
$P = 2\pi\sqrt{\frac{l}{g}}.$ (1.19)

Primenim etu formulu k pul'saciyam zvezd, prinyav "dlinu" mayatnika ravnoi radiusu zvezdy, t. e. l=R, i polozhiv uskorenie sily tyazhesti ravnym ego znacheniyu na poverhnosti zvezdy, t. e. g = GMR^-2. Opyat' vvodya vyrazhenie dlya srednei plotnosti $\bar\rho$ , poluchim iz (1.19) formulu

$P(\bar\rho)^{1/2} = \sqrt{\frac{3\pi}{G}},$ (1.20)

sootvetstvuyushuyu (1.17) pri znachenii bezrazmernogo kompleksa P₁ = 2π.

Fizicheskaya sut' yavlenii, sootvetstvuyushih pul'saciyam zvezd i kolebaniyam mayatnika, odna i ta zhe - eto mehanicheskie dvizheniya v iole tyazhesti, sootvetstvuyushie nebol'shim otkloneniyam ot polozheniya ravnovesiya. Otsyuda i blizost' chislennyh znachenii bezrazmernyh kompleksov i ih primernoe postoyanstvo dlya ob'ektov stol' razlichnyh masshtabov.

Vtoroi bezrazmernyi kompleks nado vybrat' tak, chtoby v nego voshel hotya by odin iz parametrov, kotorogo net v pervom komplekse; togda avtomaticheski obespechivaetsya ih razmernaya nezavisimost'. V etom sluchae primem k₂ = 1 i k₄ = 0, t. e. sohranim svetimost' i opustim postoyannuyu tyagoteniya. Togda reshenie sistemy (1.15) daet: k₁ = -1, k₃ = -2, k₁ = 3, i my poluchaem bezrazmernyi kompleks:

$LP^3M^{-1}R^{-2} = \Pi_2.$ (1.21)

Fizicheskii smysl etoi velichiny tozhe prostoi: eto est' otnoshenie energii, izluchennoi zvezdoi za odin period kolebaniya LP, k velichine, kotoraya harakterizuet mehanicheskuyu energiyu kolebanii zvezd MR²/P². Parametr P₁ est' nechto vrode obratnoi velichiny dobrotnosti kolebanii zvezd, no nuzhno imet' v vidu, chto energiya, dissipirovavshaya za odno kolebanie, mnogo men'she energii, izluchennoi zvezdoi za eto vremya, a velichina kineticheskoi energii pul'sacii takzhe sushestvenno men'she MR²/P², tak kak pul'siruyut tol'ko naruzhnye sloi zvezdy (t. e. malaya dolya massy zvezdy) i amplituda pul'sacii mala po sravneniyu s radiusom zvezdy.

Sopostavlyaya sootnoshenie (1.21) s dannymi nablyudenii, legko ubedit'sya, chto, vo-pervyh, bezrazmernyi kompleks P₂ vsegda na poryadki velichin men'she edinicy, a, vo-vtoryh, u raznyh zvezd ego velichina ochen' razlichna. V samom dele, u cefeid tipa RR Liry P₂ ≈ (4 ÷ 80) ⋅ 10^-9, a u klassicheskih cefeid etot kompleks menyaetsya eshe v bol'shih predelah - ot 10^-9 do 3 ⋅ 10^-3 po mere uvelicheniya perioda. Takim obrazom, v otlichie ot P₁ velichina P₂ ne mozhet schitat'sya postoyannoi. No eto uslovie takzhe sleduet i iz P-teoremy.

Soglasno etoi teoreme formula (1.11) perepisyvaetsya v vide

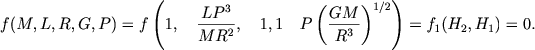
$f(M, L, R, G, P) = f\left(1, \quad \frac{LP^3}{MR^2}, \quad 1,1 \quad P\left(\frac{GM}{R^3}\right)^{1/2}\right) = f_1(H_2, H_1) = 0.$ (1.22)

Uchityvaya teper', chto P₂ << 1, zapishem:

$f_1(\Pi_2, \Pi_1) = f_1(0, \Pi_1) + \left. \Pi_2 \frac{\partial f_1}{\partial \Pi_2}\right|_{\Pi_2=0} \approx f_1(0, \Pi_1) \approx 0.$ (1.23)

Otsyuda sleduet, chto v pervom priblizhenii reshenie uravneniya f₁(0, P₁) = 0 daet nekotoroe postoyannoe znachenie lish' dlya P₁ a velichina P₂ << 1 ostaetsya neopredelennoi i poetomu mozhet sil'no menyat'sya u zvezd raznyh tipov i mass.

Takim obrazom, period pul'sacii zvezdy zavisit v pervom priblizhenii tol'ko ot srednei plotnosti. Yavnoi zavisimosti perioda ot svetimosti zdes' net. No, razumeetsya, est' neyavnaya zavisimost', poskol'ku svetimosti zvezd tozhe zavisyat ot ih massy i ot srednei plotnosti. I deistvitel'no, horosho izvestna zavisimost' period-svetimost' u peremennyh zvezd opredelennyh tipov, pozvolyayushaya ispol'zovat' eti zvezdy dlya sozdaniya shkaly rasstoyanii. K sozhaleniyu, soobrazheniya teorii razmernostei okazalis' nedostatochnymi dlya polucheniya i etoi zavisimosti, no, eshe raz podcherkivaem, sootnoshenie period - srednyaya plotnost' poluchaetsya iz soobrazhenii razmernosti srazu.

Vtoroi bezrazmernyi kompleks my vybrali bolee ili menee proizvol'no. Vozmozhen, konechno, i drugoi vybor etoi velichiny. No v lyubom sluchae ego mozhno predstavit' v vide proizvedeniya $\Pi_1^a\Pi_2^b$ gde a i b nekotorye racional'nye chisla. Otsyuda yasno, chto v lyubom sluchae vtoroi bezrazmernyi kompleks budet libo ochen' mal libo velik (v takom sluchae nado pereiti k obratnoi velichine etogo kompleksa) i iz P-teoremy po-prezhnemu sleduet tol'ko postoyanstvo pervogo bezrazmernogo kompleksa.

Vyshe my sravnili pul'sacii zvezd s kolebaniyami matematicheskogo mayatnika. Okazalos', chto osnovnoi bezrazmernyi kompleks (kriterii podobiya) v oboih sluchayah imeet blizkie znacheniya. Eto oznachaet, chto yavlenie kolebaniya zvezd i yavlenie kolebaniya mayatnika podobny po osnovnomu parametru. No, razumeetsya, vo mnogom eti yavleniya i sushestvenno razlichny. Bylo postroeno mnogo chislennyh modelei zvezdnyh pul'sacii, uchityvayushih i drugie opredelyayushie parametry (sm. gl. 5), sushestvenno otlichnye ot parametrov kolebanii mayatnika. Zdes', razumeetsya, podobiya net.

V takih sluchayah mozhno govorit' ob ogranichennom podobii yavlenii, kogda sovpadayut chislennye znacheniya lish' nekotoryh opredelyayushih bezrazmernyh kompleksov, no drugie bezrazmernye kompleksy sushestvenno razlichayutsya.

Vtoroi primer vyberem iz teorii dvizheniya tel v pole tyazhesti. Etot ochen' prostoi primer pozvolit prodemonstrirovat' vazhnyi metodicheskii priem teorii razmernostei, - tak nazyvaemoe dopolnenie Hantli (sm. [4]).

Rassmotrim horosho izvestnuyu iz mehaniki zadachu. Pust' pod uglom α k poverhnosti brosheno telo s nachal'noi skorost'yu v₀. Pod deistviem uskoreniya sily tyazhesti g telo upadet obratno na poverhnost' na nekotorom rasstoyanii l ot tochki brosaniya. Trebuetsya opredelit' etu velichinu. Iskomaya zavisimost' est'

$f(\alpha ,v_0, g, l) = 0.$ (1.24)

Sostavim matricu razmernosti:

$\begin{matrix} \, & [\alpha] & [v_0] & [g] & [l] \\ \mbox{sm}&0&1&1&1 \\ \mbox{sek}&0&-1&-2&0 \end{matrix}$

Odin iz bezrazmernyh kompleksov ocheviden - sama bezrazmernaya velichina α , t. e.

$\Pi_1 = \alpha .$ (1.25)

Vtoroi bezrazmernyi kompleks ishem v vide $\Pi_2 = lv_0^{k_1} g^{k_2}$ , otkuda nahodim

$\Pi_2 = lgv_0^{-2} .$ (1.26)

Sledovatel'no, vmesto (1.24) imeem

$f\left(\alpha, \frac{lg}{v_0^2},\quad 1,1\right) = f_1\left(\alpha, \frac{lg}{v_0^2}\right) = 0.$ (1.27)

Eto sootnoshenie mozhno perepisat' i v vide

$l = \mbox{const} \cdot \frac{v_0^2}{g}\phi (\alpha),$ (1.28)

gde φ(α) - nekotoraya neizvestnaya funkciya. Kazalos' by, metodom teorii razmernostei ee opredelit' nel'zya. No okazyvaetsya, chto eto vse zhe mozhno sdelat', esli schitat' gorizontal'nye (x) i vertikal'nye (u) koordinaty, imeyushimi raznye razmernosti. Togda i komponenty skorosti v_0x=v₀sinα i v_0y=v₀cosα takzhe imeyut raznye razmernosti. V etom sluchae matrica razmernosti:

$\begin{matrix} \, & [v_0x] & [v_0y] & [g] & [l] \\ x&1&0&0&1 \\ y&0&1&1&0 \\ \mbox{sek}&-1&-1&-2&0 \end{matrix}$

Etoi matrice sootvetstvuet tol'ko odin bezrazmernyi kompleks

$\Pi = lgv_{0x}^{-1}v_{0y}^{-1} = lg v_{0}^{-2}(\sin\alpha\cos\alpha)^{-1} ,$ (1.28)

otkuda imeem

$l = \mbox{const} \cdot \frac{v_0^2}{g}\sin 2\alpha .$ (1.30)

Tem samym funkciya φ(α) v (1.28) okazalas' opredelennoi.

Metod pripisyvaniya fiktivnoi raznoi razmernosti velichinam s odinakovymi fizicheskimi razmernostyami mozhet okazat'sya poleznym i v drugih sluchayah. Metodami teorii razmernostei mozhno opredelit' mnogie fizicheskie .parametry, neobhodimye dlya astrofizicheskih issledovanii. Naprimer, mozhno ocenit' razmer atoma vodoroda α₀ i ego energiyu ionizacii χ_H. Ochevidno, chto eti velichiny opredelyayutsya massoi elektrona m_e i ego zaryadom e. Krome togo, poskol'ku atom vodoroda yavlyaetsya kvantovomehanicheskoi sistemoi, v chislo opredelyayushih parametrov vhodit i postoyannaya Planka ħ . Takim obrazom, imeem sleduyushuyu matricu razmernostei:

$\begin{matrix} \, & [a_0] & [\chi_H] & [m_e] & [e] & [\hbar] \\ \mbox{g}&0&1&1&1/2&1 \\ \mbox{sm}&1&2&0&3/2&2 \\ \mbox{sek}&0&-2&0&-1&-1 \end{matrix}$

Kak i ran'she, ishem bezrazmernye kompleksy v vide

$a_0^{k_1}\chi_H^{k_2}m_e^{k_3}e^{k_4}\hbar^{k_5} = \Pi.$ (1.31)

Reshaya sistemu sootvetstvuyushih uravnenii dlya pokazatelei k_i, nahodim dva resheniya, prichem v pervom prinimaem k₁ = 1, k₂ = 0, a vo vtorom k₁ = 0, k₂ = 1. V rezul'tate poluchaem dva kompleksa:

$\Pi_1 = a_0m_ee^2\hbar^{-2}, \quad \Pi_2 = \chi_H\hbar^2m_e^{-1}e^{-4}.$

Tochnaya teoriya daet dlya chislennyh znachenii bezrazmernyh kompleksov velichiny P₁ = 1, P₂=½ . Takim obrazom,

$a_0 = \frac{\hbar^2}{m_ee^2}, \quad \chi_H = \frac{m_ee^4}{2\hbar^2}.$ (1.32)

Obe velichiny igrayut vazhnuyu rol' i v astrofizike.

Analogichnym obrazom mozhno naiti harakternyi razmer atomnogo yadra a_N i velichinu energii svyazi nuklonov v yadre χ_N. Dlya etogo v sootnosheniyah (1.32) sleduet zamenit' m_e na massu nuklona m_N i vvesti vmesto e velichinu g, harakterizuyushuyu yadernoe vzaimodeistvie.

Soglasno Vaiskopfu [13] potencial prityazheniya mezhdu nuklonami na ih srednem rasstoyanii v yadre mozhet byt' approksimirovan elektrostaticheskim potencialom s g ≈ 3,3e, t. e. g² ≈ 10e². Poetomu dlya harakteristik atomnogo yadra poluchim vmesto (1.32)

$a_N = \frac{\hbar^2}{m_Ng^2} \approx \frac{a_0}{2 \cdot 10^4}, \quad \chi_N = \frac{m_Ng^2}{2\hbar^2} \approx 2\cdot 10^5\chi_H.$ (1.33)

Nakonec, kak poslednii primer, illyustriruyushii znachenie podobiya v astrofizike, rassmotrim opredelenie radiusa zon ionizacii Stremgrena. Izvestno, chto vokrug kazhdoi goryachei zvezdy v mezhzvezdnom gaze obrazuetsya zona ionizovannogo vodoroda. Vnutri ee vodorod pochti polnost'yu ionizovan, vne ee - pochti neitralen. Granica zony ionizacii dostatochno rezkaya. Vo vsyakom sluchae tolshina perehodnoi oblasti mnogo men'she radiusa zon ionizacii. Velichinu radiusa zon ionizacii vodoroda s0 legko ocenit', vospol'zovavshis' tem usloviem, chto vnutri zony Stremgrena chislo ionizacii za edinicu vremeni ravno chislu rekombinacii za eto zhe vremya.

Pust' zvezda radiusa R ispuskaet s edinicy ploshadi poverhnosti za edinicu vremeni N_L kvantov, sposobnyh ionizovat' atomy vodoroda. Chislo rekombinacii proporcional'no proizvedeniyu koncentracii svobodnyh elektronov n_e i protonov n_p. Koefficient proporcional'nosti oboznachim cherez α_t. Razmernosti dvuh novyh velichin est'

$[N_L] = \frac{1}{\mbox{sm}^2 \cdot \mbox{sek}}, \quad [\alpha_t] = \frac{\mbox{sm}^3}{\mbox{sek}}.$ (1.34)

Uslovie ravenstva chisla ionizacii i rekombinacii est'

$4\pi R^2N_L = \alpha_t n_e n_p \frac{4\pi}{3}s_0^3.$ (1.35)

Zdes' predpolagaetsya sferichnost' zony ionizacii. Koefficient rekombinacii zavisit tol'ko ot temperatury, i poskol'ku temperatury raznyh zon ionizacii menyayutsya malo, to α_t , mozhno schitat' priblizitel'no postoyannoi. V oblasti polnoi ionizacii n_e ≈ n_p. Poetomu

$s_0 = \sqrt[3]{\frac{3R^2N_L}{\alpha_tn_e^2}} = \frac{U(Sp)}{n_e^{2/3}},$ (1.36)

gde U(Sp) est' nekotoraya velichina, zavisyashaya ot spektral'nogo tipa zvezd. Ee mozhno rasschitat' teoreticheski na osnove modelei atmosfer zvezd, mozhno takzhe opredelit' i po dannym nablyudenii. Teoreticheskie p nablyudatel'nye znacheniya U(Sp) dostatochno blizki.

Sootnosheniya (1.36) sleduet rassmatrivat' kak uslovie podobiya - u zvezd odnogo i togo zhe spektral'nogo klassa velichiny $s_0n_e^{2/3}$ odinakovy. Eto uslovie mozhno ispol'zovat' dlya ocenki s₀ pri izvestnom n_e i naoborot. Mozhno takzhe ocenit' i massu gaza vnutri zony Stremgrena:

$M_s = \frac{4\pi}{3}s_0^3n_em_p,$ (1.37)

gde m_p - massa protona. Podstavlyaya syuda (1.36), nahodim

$M_s = \frac{4m_p}{n_e}[U(\mbox{Sp})]^3,$ (1.38)

Zdes' kriterii podobiya zaklyuchaetsya v tom, chto M_sn_e est' postoyannaya velichina dlya zvezd dannogo spektral'nogo klassa. Lyubopytno, chto M_s mnogo bol'she massy zvezd, naprimer, u zvezd klassa O7 imeem U(Sp) = 62 ps sm^-2 M_sn_e ≈ 10⁴M_☉ ⋅ 1 sm^-3 .

My zdes' ogranichimsya tol'ko etimi prostymi primerami. V posleduyushih glavah budut mnogokratno ispol'zovany metody analiza razmernostei dlya polucheniya razlichnyh sootnoshenii mezhdu astrofizicheskimi velichinami. Mnogo razlichnyh sootnoshenii podobiya budut ispol'zovany dlya ob'yasneniya nablyudaemyh zavisimostei.

No, primenyaya metody teorii razmernostei i podobiya, vsegda nuzhno imet' v vidu, chto vybor ishodnyh parametrov opredelyaetsya fizikoi yavleniya, a otnyud' ne odnimi soobrazheniyami razmernosti. Esli pri sostavlenii spiska opredelyayushih parametrov ne budut uchteny nekotorye vazhnye velichiny, to soobrazheniya analiza razmernostei i podobiya mogut privesti k oshibochnym vyvodam.

I nakonec poslednee. Kak neodnokratno podcherkivalos', chislennoe znachenie "znachashih" bezrazmernyh kompleksov, yavlyayushihsya k tomu zhe i kriteriyami podobiya, iz soobrazhenii razmernostei ne opredelyaetsya. No chasto eti kompleksy deistvitel'no malo otlichayutsya ot edinicy. Eto obshee svoistvo mozhno ob'yasnit' i tak. Esli rassmatrivaemyi ob'ekt nahoditsya v ravnovesnom sostoyanii, to eto oznachaet, chto primerno ravny dve protivopolozhno deistvuyushie sily, naprimer, sila tyagoteniya i sila gazovogo davleniya (v sluchae zvezdy), ili sila kulonovskogo prityazheniya i kvantovogo "shredingerovskogo davleniya", po opredeleniyu Vaiskopfa [13], pri nahozhdenii velichin α₀ i χ_H soglasno (1.33). Bezrazmernyi kompleks est' otnoshenie velichin etih sil, v sluchae ih ravenstva v ravnovesnom sostoyanii etot kompleks dolzhen byt' blizok k edinice.

<< § 1.3 Podobie i modelirovanie | Oglavlenie | § 1.5 Mirovye (fundamental'nye) postoyannye >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce