Astronet > Razmernosti i podobie astrofizicheskih velichin

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 2.1 Opredelyayushie parametry gravitacii | Oglavlenie | § 2.3 Harakternye parametry tverdyh planet >>

§ 2.2 Vzaimodeistvie elektromagnitnogo izlucheniya i veshestva

Issledovanie vzaimodeistviya izlucheniya i veshestva predstavlyaet soboi odnu iz central'nyh problem astrofiziki.

Vo-pervyh, pochti vsya poluchaemaya nami informaciya o fizicheskih svoistvah nebesnyh tel soderzhitsya v ih izluchenii.

Vo-vtoryh, sami svoistva etih tel, ih struktura i dinamika opredelyayutsya naryadu s gravitaciei takzhe i transformaciei luchistoi energii v etih telah. Vozmozhnost' kondensacii kosmicheskoi sredy v bolee plotnye ob'ekty - zvezdy, sama struktura zvezdy i ee evolyuciya, stroenie i osobennosti povedeniya mezhzvezdnogo gaza - vse eto v toi ili inoi mere zavisit ot perenosa luchistoi energii v veshestve. Zakony izlucheniya, i v chastnosti, sootnosheniya, opisyvayushie vzaimodeistvie elektromagnitnogo izlucheniya i veshestva, horosho izvestny; vo mnogih sluchayah imeyutsya tochnye formuly, shiroko ispol'zuemye v astrofizike. Kazalos' by, chto metody analiza razmernostei zdes' ne nuzhny, razve tol'ko dlya proverki pravil'nosti napisaniya formul.

Odnako, kak my seichas uvidim, razmernostnyi analiz pozvolyaet kak by po-novomu vzglyanut' na uzhe izvestnye formuly, luchshe ponyat' ih fizicheskii smysl. A glavnoe dlya astrofiziki eto to, chto razmernostnyi analiz pozvolyaet uprostit' osnovnye sootnosheniya, kogda izlishnee utochnenie tol'ko zatemnyaet fiziku yavleniya. V etom paragrafe my provedem analiz ryada osnovnyh formul, znakomyh kazhdomu astrofiziku, i poluchim sootnosheniya, kotorye nam ponadobyatsya v dal'neishem dlya analiza metodom razmernostei drugih zadach.

Nachnem s horosho izvestnoi formuly Planka dlya intensivnosti termodinamicheski ravnovesnogo izlucheniya

$I_\nu = B_\nu(T) = \frac{2h\nu^3}{c^2}\frac{1}{e^{\frac{h\nu}{kT}} - 1},$ (2.32)

gde chastota &nu = &omega/2&pi i postoyannaya Planka h = 2&piħ.

Znaya razmernosti velichin, vhodyashih v formulu (2.32), mozhno postroit' matricu razmernosti:

$\begin{matrix} \, & [h] & [\nu] & [c] & [I_\nu]&[k]&[T] \\ \mbox{g}&1&0&0&1&1&0 \\ \mbox{sm}&2&0&1&0&2&0 \\ \mbox{sek}&-1&-1&-1&-2&-2&0 \\ \mbox{grad}&0&0&0&0&-1&1 \end{matrix}$

U nas shest' parametrov pri chetyreh pervichnyh velichinah, tak chto soglasno P-teoreme dolzhno byt' dva bezrazmernyh kompleksa. Dva iz pokazatelei stepenei mozhno vybrat' proizvol'no; polagaya pokazatel' pri I_&nu ravnym edinice, a pokazatel' pri postoyannoi Planka - nulyu, poluchim pervyi bezrazmernyi kompleks

$\Pi_1 = c^2I_\nu k^{-1}T^{-1}\nu^{-2},$ (2.33)

Dlya nahozhdeniya vtorogo kompleksa primem pokazatel' pri I_&nu ravnym nulyu, a pokazatel' pri postoyannoi Planka - edinice. Poluchim

$\Pi_2 = h\nu k^{-1}T^{-1}.$ (2.34)

Togda formula Planka zapishetsya v vide zavisimosti bezrazmernogo kompleksa P₁ ot kompleksa P₂:

$f(\Pi_1,\Pi_2) = \Pi_1 - \frac{2\Pi_2}{e^{\Pi_2}-1}=0.$ (2.35)

Konkretnyi vid funkcii &fnof(P₁, P₂) opredelen ne metodom razmernostei, odnako dazhe suzhdenie ob argumentah funkcii, poluchaemyh posredstvom razmernostnoi procedury, chasto okazyvaetsya dostatochnym dlya mnogih celei. V tom sluchae, kogda odin iz bezrazmernyh kompleksov mal (naprimer, v radiodiapazoie P₂ << 1), iz usloviya &fnof(P₁, P₂) = 0 sleduet, chto P₁ = const, a iz yavnogo vida etoi funkcii poluchaem, chto P₁ = 2. Otsyuda imeem zakon Releya - Dzhinsa:

$I_\nu = \frac{2\nu^2}{c^2}kT,$ (2.36)

kotoryi, kstati, pervonachal'no i byl poluchen iz soobrazhenii razmernosti. Esli P₂ ne malo, to, razumeetsya, odnoznachnoi formuly iz odnih soobrazhenii razmernosti ne poluchit'.

Pri proizvol'nyh znacheniyah P₁ i P₂ eti kompleksy mogut sluzhit' kriteriem podobiya. Izvestno, chto spektral'nye krivye raspredeleniya energii imeyut maksimum. Kriterii podobiya oznachaet, chto maksimumy izlucheniya pri raznyh temperaturah sootvetstvuyut odnim i tem zhe znacheniyam bezrazmernyh kompleksov, a imenno P₂ = 2,82, P₁ = 0,35. Eto est' izvestnyi zakon smesheniya Vina:

$\lambda_m = \frac{c}{\nu_m} = \frac{1}{\Pi_2}\frac{hc}{kT} = \frac{0,29}{T}\mbox{sm},$ (2.37)

esli temperatura vyrazhena v gradusah. V (2.37) i posleduyushih formulah intensivnost' izlucheniya otnesena k edinichnomu intervalu chastot - ves' analiz netrudno provesti i v sluchae, kogda spektral'naya intensivnost' otnesena k edinichnomu intervalu dlin voln. V etom sluchae izmenitsya opredelenie bezrazmernogo kompleksa P₁ no funkciya &fnof(P₁, P₂) budet imet' prezhnii vid. Neskol'ko smestitsya i polozhenie maksimuma v zakone Vina (2.37).

Drugoe horosho izvestnoe v astrofizike sootnoshenie - formula Saha - opredelyaet stepen' ionizacii. Esli cherez n_s, n_e i n₁ oboznachit' koncentraciyu atomov, elektronov i ionov dannogo elementa, to formula Saha zapisyvaetsya v vide

$\frac{n_in_e}{n_a} = 2\frac{g_i}{g_a}\frac{(2\pi m_ekT)^{3/2}}{h^3}e^{-\frac{\chi}{kT}}.$ (2.38)

Zdes' &chi - potencial ionizacii, g_a i g_i - statisticheskie vesa atoma i iona. Ogranichimsya sluchaem vodoroda i primem v dal'neishem g_a = g_i = 2 (dlya osnovnogo sostoyaniya).

Chtoby zapisat' uravnenie Saha s pomosh'yu bezrazmernyh kompleksov, vspomnim opredelenie debroilevskoi dliny volny elektrona &lambda = h/m_ev, gde v - ego skorost'. U teplovyh elektronov skorost' proporcional'na (kT/m_e)^½ i poetomu dlya nih

$\lambda_h = \frac{h}{\sqrt{2\pi m_ekT}}.$ (2.39)

Teper' opredelim sleduyushie bezrazmernye kompleksy:

$\Pi_1 = \frac{n_i}{n_a}$ - otnoshenie koncentracii ionov k koncentracii atomov;

$\Pi_2 = \frac{\chi_H}{kT}$ - otnoshenie energii ionizacii k teplovoi energii chastic;

$\frac{1}{\Pi_3} = n_e\lambda_h^3$ - kolichestvo elektronov v yacheike prostranstva s razmerom, ravnym debroilevskoi dline volny.

Ochevidno, chto kompleks P₃ harakterizuet kolichestvo elektronov, sposobnyh okazat'sya vblizi atoma ili iona i uchastvovat' v processah ionizacii i rekombinacii.

S opredelennymi vyshe bezrazmernymi kompleksami formula Saha zapisyvaetsya v ochen' prostom vide:

$\Pi_1 = 2\Pi_3e^{-\Pi_2}.$ (2.40)

Mozhno privesti i drugie primery zapisi horosho izvestnyh astrofizicheskih formul v vide sootnoshenii mezhdu bezrazmernymi kompleksami.

Teper' pereidem k parametram, opisyvayushim vzaimodeistvie izlucheniya s veshestvom i neobhodimym nam dlya dal'neishego izlozheniya - v pervuyu ochered' k opredeleniyu koefficientov poglosheniya i neprozrachnosti.

Esli otnesti koefficient poglosheniya ili rasseyaniya k odnomu atomu, ionu ili elektronu, to takuyu velichinu prinyato nazyvat' effektivnym secheniem i oboznachat' bukvoi &sigma_&nu. Ee razmernost'

$[\sigma_\nu] = \mbox{sm}^2.$ (2.41)

Umnozhiv effektivnoe sechenie na chislo pogloshayushih ili rasseivayushih chastic v edinice ob'ema, poluchim koefficient poglosheniya k_&nu, rasschitannyi na edinicu dliny. Poetomu ego razmernost'

$[k_\nu] = \frac{1}{\mbox{sm}}.$ (2.42)

I nakonec, otnosya koefficient poglosheniya k edinice plotnosti, poluchim velichinu koefficienta neprozrachnosti $\varkappa$ s razmernost'yu

$[\varkappa_\nu] = \frac{\mbox{sm}^2}{\mbox{g}}.$ (2.43)

Strogo govorya, perehod ot (2.41) k (2.42) i (2.43) ne svoditsya k prostomu umnozheniyu na koncentraciyu ili deleniyu na plotnost'. Operaciya perehoda provoditsya s usredneniem po funkcii raspredeleniya chastic i po spektru. V astrofizicheskih uchebnikah eti operacii podrobno obsuzhdayutsya (sm. [3, 4]). Zdes' my tol'ko privedem gotovye formuly i obsudim ih s tochki zreniya razmernostei.

Neprozrachnost' veshestva vklyuchaet v sebya i chistoe rasseyanie i pogloshenie. Ego chasto nazyvayut ekstinkciei. No v nashei literature ukorenilsya termin pogloshenie, kotorym my i budem pol'zovat'sya.

Prosteishim mehanizmom vzaimodeistviya izlucheniya i veshestva yavlyaetsya tomsonovskoe rasseyanie sveta na svobodnyh elektronah. Zdes' effektivnoe sechenie ne zavisit ot chastoty:

$\sigma_\nu^T=\frac{8\pi}{3}r_0^2 = \frac{8\pi}{3}\left(\frac{e^2}{m_ec^2}\right)^2 = \frac{8\pi}{3}\alpha^2\lambda_K^2.$ (2.44)

Opredelenie vhodyashih syuda velichin dano v § 5 gl. 1. Vyrazhenie $\sigma_\nu^T$ cherez komptonovskuyu dlinu volny &lambda_K i postoyannuyu tonkoi struktury a nam ponadobitsya dlya sravneniya s drugimi mehanizmami.

Koefficient neprozrachnosti pri tomsonovskom rasseyanii raven

$\varkappa_\nu^T = \frac{8\pi}{3}\frac{\alpha^2\lambda_K^2}{m_p\mu_e} = \frac{8\pi}{3}\frac{e^4}{m_e^2m_pc^4},$ (2.45)

gde &mu_K - molekulyarnyi ves, prihodyashiisya na odin svobodnyi elektron. Sushestvenno, chto vyrazhenie (2.45) postoyanno i za isklyucheniem mnozhitelya c.e zavisit tol'ko ot mirovyh konstant.

Sleduyushii "po slozhnosti" mehanizm - pogloshenie ili rasseyanie elektromagnitnyh voln pri perehodah elektrona mezhdu diskretnymi sostoyaniyami atomov ili ionov. Oboznachim cherez v0 chastotu perehoda.

V etom mehanizme effektivnoe sechenie sushestvenno zavisit ot chastoty. Ono dostigaet maksimuma na chastote perehoda i bystro spadaet v obe storony s rostom raznosti |&nu - &nu₀|, gde &nu - chastota rasseivaemoi ili pogloshaemoi volny. Formula dlya effektivnogo secheniya:

$\sigma_\nu = \frac{2\pi}{3}\frac{r^2_0 \nu_0^2 f}{(\nu - \nu_0)^2 + \left(\frac{\gamma}{4\pi}\right)^2},$ (2.46)

gde &fnof est' sila oscillyatora, bezrazmernyi mnozhitel', pokazyvayushii, naskol'ko process rasseyaniya pri perehodah v atome otlichaetsya ot takogo zhe perehoda v sluchae rasseyaniya sveta klassicheskim oscillyatorom. Velichina

$\gamma = \frac{8\pi^2c^2\nu_0^2}{3m_ec^3} = \frac{8\pi^2}{3}\frac{r_0\nu_0^2}{c} << \nu_0$ (2.47)

est' tak nazyvaemaya estestvennaya shirina linii. Maksimum effektivnogo secheniya v centre linii (&nu = &nu₀) ochen' velik:

$\sigma_\nu^{max} = \frac{3f}{2\pi}\frac{c^2}{\nu_0^2} = \frac{3f}{2\pi}\lambda_0^2,$ (2.48)

no bystro spadaet pri |&nu - &nu₀| >> &gamma . Pri |&nu - &nu₀|, sravnimym s &nu₀, effektivnoe sechenie (2.46) dast primerno stol'ko zhe, skol'ko tomsonovekoe sechenie. V celom rasseyanie v spektral'nyh liniyah mozhet dat' zametnyi vklad v polnyi koefficient neprozrachnosti sredy, no obshii poryadok velichiny mozhno ocenit' po tomu zhe tomsonovskomu secheniyu.

Formuly (2.44), (2.48) i drugie posleduyushie formuly naglyadno pokazyvayut, chto effektivnoe sechenie dolzhno predstavlyat' soboi proizvedenie dvuh parametrov s razmernost'yu dliny. V sluchae (2.44) eto bylo r₀, v sluchae (2.48) my poluchili &lambda₀ - dlinu volny, v ostal'nyh sluchayah budut vstrechat'sya i drugie kombinacii.

Sushestvenno bol'shii vklad v koefficient poglosheniya vnosyat perehody iz svyazannogo sostoyaniya v svobodnoe, t. e. ionizaciya atomov i ionov. Zapishem effektivnoe sechenie dlya poglosheniya s pervogo urovnya atoma vodoroda:

$\sigma_\nu^{(1)} = \frac{64\pi}{3\sqrt3}a_0\lambda_K\left(\frac{\nu_1}{\nu}\right)^3 g(\nu) = \frac{64\pi}{3\sqrt3}\frac{r^2_0}{\alpha^3}\left(\frac{\nu_1}{\nu}\right)^3 g(\nu),$ (2.49)

gde &nu₁=&chi_H/h - chastota poroga ionizacii, g(&nu) - ochen' medlenno menyayushayasya bezrazmernaya funkciya chastoty. Vblizi poroga pri &nu = &nu₁ g(&nu₁)=0,80, a srednee znachenie etoi velichiny po spektru primerno ravno 0,89. Formuly, analogichnye (2.49), poluchayutsya i dlya drugih urovnei kak atoma vodoroda, tak i drugih atomov. Zdes' menyaetsya chislennyi koefficient i, voobshe govorya, okazyvaetsya bolee slozhnaya zavisimost' ot chastoty.

Effektivnoe sechenie (2.49) v maksimume pri &nu = &nu₁ ochen' veliko. Sravnivaya (2.49) s tomeonovekim secheniem (2.47), poluchim

$\frac{\sigma_\nu^{max}}{\sigma_\nu^T} = \frac{8}{\sqrt 3}\frac{1}{\alpha^3} = 1,2 \cdot 10^6,$ (2.50)

no pri usrednenii po chastotam eto razlichie, estestvenno, zametno umen'shaetsya. Procedura usredneniya zavisit ot mnogih uslovii, v chastnosti, ot (raspredeleniya energii v spektre pogloshaemogo izlucheniya, ot raspredeleniya atomov po sostoyaniyam i t. d. Otsylaya chitatelya za podrobnostyami k literature [3, 4], privedem zdes' okonchatel'nuyu razmernostnuyu formulu, t. e. bez chislennyh mnozhitelei poryadka edinicy, dlya srednego effektivnogo secheniya etih tak nazyvaemyh svobodno-svyazannyh perehodov. Imeem dlya secheniya, otnesennogo k odnomu atomu:

$\bar\sigma \sim \alpha r_T^2\frac{\chi_H}{kT}e^{-\frac{\chi_H}{kT}}.$ (2.51)

Pri usrednenii prinyato, chto raspredelenie energii v spektre izlucheniya opisyvaetsya formuloi Planka, a raspredelenie po sostoyaniyam - uravneniem Bol'cmana.

Velichinu r_T s razmernost'yu dliny

$r_T = \frac{e^2}{kT}.$ (2.52)

mozhno bylo by nazvat' "teplovym radiusom elektrona", po analogii s klassicheskim radiusom elektrona r₀ = e²/m_ec². Ochevidno, chto chem bol'she temperatura, tem (bystree dvizhutsya elektrony i tem men'she veroyatnost' ih vzaimodeistviya s atomami.

Sleduyushii vazhnyi mehanizm vzaimodeistviya izlucheniya i veshestva - eto pogloshenie v nepreryvnom spektre pri tak nazyvaemyh svobodno-svobodnyh perehodah. Pogloshenie proishodit pri perehode elektrona s odnoi giperbolicheskoi orbity na druguyu pri prolete ego mimo polozhitel'no zaryazhennogo elektrona.

Srednee effektivnoe sechenie etogo processa, uzhe usrednennoe po maksvellovskoi funkcii raspredeleniya skorostei elektronov i po plankovskomu spektru izlucheniya i otnesennoe k odnomu ionu, imeet vid:

$\bar\sigma^{ff} \sim \alpha r_T^2 n_e\lambda_h^3 = \alpha^3\left(\frac{\hbar c}{kT}\right)^2\lambda_h^3 n_e.$ (2.53)

Uchityvaya uravnenie Saha, mozhno ubedit'sya, chto pri vysokih temperaturah (T &ge 3 &sdot 10⁵ grad) svobodno-svobodnye perehody okazyvayutsya opredelyayushimi.

Perehodya ot $\bar\sigma^{ff}$ k koefficientu neprozrachnosti

$\varkappa = const \cdot \frac{\alpha^3 n_e \lambda_h^3}{\mu_e m_p}\left(\frac{\hbar c}{kT}\right)^2 ,$

poluchim horosho izvestnuyu formulu Kramersa, kotoruyu obychno zapisyvayut v vide

$\varkappa = \varkappa_0 \rho T^{-\frac{7}{2}},$ (2.54)

gde razmernyi koefficient $\varkappa_0$ proporcionalen sleduyushemu naboru fundamental'nyh postoyannyh:

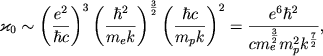
$\varkappa _0 \sim \left(\frac{e^2}{\hbar c}\right)^3 \left(\frac{\hbar^2}{m_e k}\right)^{\frac{3}{2}} \left(\frac{\hbar c}{m_p k}\right)^2 = \frac{e^6\hbar^2}{cm_e^{\frac{3}{2}}m_p^2 k^{\frac{7}{2}}},$ (2.55)

Ego razmernost'

$[\varkappa_0] = \frac{\mbox{sm}^5 \cdot \mbox{grad}^{7/2}}{\mbox{g}^2} .$ (2.56)

Krome fundamental'nyh atomnyh postoyannyh v k₀ vhodyat bezrazmernye mnozhiteli, zavisyashie ot sostoyaniya ionizacii veshestva i ego himicheskogo sostava. Poskol'ku ionizaciya veshestva menyaetsya s temperaturoi i plotnost'yu, to velichinu koefficienta neprozrachnosti v nastoyashee vremya chashe vsego uzhe ne opisyvayut prostoi formuloi Kramersa, a zadayut v tablichnom vide. Odnako dlya primeneniya metoda analiza razmernostei nam vse zhe budut nuzhny analiticheskie formuly. Podrobnee, vopros o koefficiente (neprozrachnosti v nedrah zvezd - my obsudim v gl. 5. Tam zhe budut dany i sootvetstvuyushie approksimacionnye formuly.

Na nizkih chastotah, naprimer, v radiodiapazone, takzhe preobladaet pogloshenie pri svobodno-svobodnyh perehodah. No zdes' vazhna rol' inducirovannyh processov, kogda akt poglosheniya stimuliruetsya nalichiem v srede izlucheniya na teh zhe chastotah. Effektivnoe sechenie, usrednennoe po makovellovskomu raspredeleniyu skorostei i uchityvayushee inducirovannye processy, imeet vid

$\sigma_\nu = \frac{2}{3\sqrt{2\pi}}\alpha^3n_e \lambda_h^3\lambda^2 g.$ (2.57)

Zdes' &lambda - dlina pogloshaemoi volny i g - mnozhitel' Gaunta, logarifmicheski zavisyashii ot temperatury i koncentracii elektronnogo gaza. Formula (2.57) ispol'zuetsya v radioastronomii, gde koefficient poglosheniya obychno otnosyat ne k edinice plotnosti, a k edinice ob'ema, i poetomu imeem

$k_\nu = \frac{2\pi}{3\sqrt 3}n_e n_i \lambda_h^3\lambda^2 g = k_0\frac{n_e n_i}{T^{3/2}}\lambda^2 g,$ (2.58)

gde

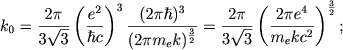
$k_0 = \frac{2\pi}{3\sqrt 3} \left(\frac{e^2}{\hbar c}\right)^3 \frac{(2\pi\hbar)^3}{(2\pi m_e k)^{\frac{3}{2}}} = \frac{2\pi}{3\sqrt 3} \left(\frac{2\pi e^4}{m_e k c^2}\right)^{\frac{3}{2}};$ (2.59)

a mnozhitel' Gaunta sootvetstvuyushei oblasti chastot kosmicheskogo radioizlucheniya

$g = \frac{\sqrt 3}{\pi}\ln\frac{4kT}{e^2\sqrt[3] {n}}.$ (2.60)

Razmernost' parametra k₀ est'

$[k_0] = \mbox{sm}^2 \cdot \mbox{grad}^{3/2}.$ (2.61)

Mehanizmy poglosheniya vsegda svyazany i s mehanizmami izlucheniya. V chastnosti, obratnym mehanizmu poglosheniya, opisyvaemogo secheniem (2.49), yavlyaetsya process rekombinacii, pri kotoroi elektron, popadaya na atomnyi uroven', izluchaet kvant elektromagnitnoi volny. Vyrazhenie dlya effektivnogo secheniya rekombinacii pri popadanii elektrona srazu na pervyi uroven' est'

$\sigma_1 = \frac{32\pi}{3\sqrt 3} \alpha \lambda_K^2 \frac{\nu_1^2 g(\nu)}{\nu (\nu - \nu_1)},$ (2.62)

gde g(&nu) - tot zhe mnozhitel' Gaunta, chto i v (2.49), i &nu₁ - po-prezhnemu chastota poroga ionizacii.

Velichina h(&nu - &nu₁) est' energiya rekombiniruyushego elektrona, i poetomu dlya polucheniya koefficienta rekombinacii v edinice ob'ema sleduet (2.62) usrednit' po maksvellovskoi funkcii raspredeleniya skorostei. V rezul'tate poluchim, chto polnoe chislo rekombinacii v edinice ob'ema, proporcional'noe $\sigma_1 \bar v n_e n_i$ gde $\bar v$ - srednyaya skorost' elektronov, zapisyvaetsya v vide

$\alpha_t n_e n_i = \frac{16\pi}{3\sqrt 3} \alpha \lambda_h ^2 \nu_1 n_e n_i f(T),$ (2.63)

gde &fnof(T) - nekotoraya bezrazmernaya funkciya, slabo zavisyashaya tol'ko ot temperatury.

Osnovnym parametrom, harakterizuyushim chislo rekombinacii, est' velichina &alpha_t s razmernost'yu

$[\alpha_t] = \frac{\mbox{sm}^3}{\mbox{sek}},$ (2.64)

uzhe ispol'zovannaya v formulah (1.34) - (1.36) . V sootvetstvii so svoei razmernost'yu, eta velichina sostoit iz proizvedeniya kuba debroilevokoi dliny volny i chastoty izlucheniya. Mnozhitel' &alpha³ harakterizuet maluyu veroyatnost' effekta radiacionnoi rekombinacii, svyazannuyu s otnositel'noi slabost'yu elektromagnitnyh vzaimodeistvii. Delo v tom, chto vsegda rekombinaciya proishodit s uchastiem treh tel (odno iz nih - foton) - eto neobhodimo dlya odnovremennogo vypolneniya zakonov sohraneniya energii i impul'sa.

Iz (2.64) sleduet i zavisimost' &alpha_t ot temperatury. Esli prenebrech' funkciei &fnof(T), to &alpha_t &sim T^-3/2; bolee tochnyi uchet raznyh zavisimostei daet &alpha_t &sim T^-1,3.

V issledovanii mezhzvezdnoi sredy bol'shoe znachenie imeet opredelenie effektivnyh sechenii vozbuzhdenii atomov elektronnym udarom. Obychno ih zapisyvayut v vide

$\sigma_i = \pi\lambda_h^2 \Omega_i,$ (2.65)

gde &lambda_h, po-prezhnemu, opredeleno formuloi (2.39), a bezrazmernaya velichina &Omega_i (poryadka edinicy) nazyvaetsya "siloi elektronnogo udara".

Razumeetsya, vse privedennye zdes' formuly horosho izvestny, - no sleduet obratit' vnimanie na to, chto razmernostnyi analiz etih formul pozvolyaet legko vyyavit' ih zavisimosti ot drugih parametrov i ob'yasnit' fizicheskii smysl etih zavisimostei.

V zaklyuchenie etogo razdela zametim, chto s pomosh'yu teorii .analiza razmernostei mozhno issledovat' i vzaimodeistvie izlucheniya s gravitacionnymi polyami (v chastnosti i v ramkah obshei teorii otnositel'nosti). Osobennost' zdes' v tom, chto i elektromagnitnoe pole i pole gravitacii opisyvayutsya ne skalyarnymi velichinami, a tenzorami. Poetomu prihoditsya nahodit' ne bezrazmernye kompleksy, a bezrazmernye skalyary, sostavlennye iz tenzornyh velichin. Primer takogo rascheta byl priveden v rabote N. R. Sibgatullina [5], gde byla ocenena dlina puti zametnogo umen'sheniya intensivnosti elektromagnitnoi volny iz-za vzaimodeistviya s sobstvennym magnitnym polem. Elektromagnitnyi tenzor proporcionalen proizvedeniyu komponent elektromagnitnogo polya v volne E_iE_j &sim E²; gravitacionnoe pole opredelyaetsya parametrami G i s. Sostaviv iz parametrov E², G i s velichinu s razmernost'yu dliny, naidem rasstoyanie zametnogo gravitacionnogo zatuhaniya elektromagnitnoi volny

$l \sim \frac{c^2}{\sqrt{GE^2}}.$ (2.66)

Dlya obychnyh elektromagnitnyh voln ot astrofizicheskih ob'ektov dlina ih gravitacionnogo zatuhaniya ochen' velika.

<< § 2.1 Opredelyayushie parametry gravitacii | Oglavlenie | § 2.3 Harakternye parametry tverdyh planet >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce