Astronet > Razmernosti i podobie astrofizicheskih velichin

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 2.2 Vzaimodeistvie elektromagnitnogo izlucheniya i veshestva | Oglavlenie | § 3.1 Sootnoshenie massa — svetimost' >>

§ 2.3 Harakternye parametry tverdyh planet

V posleduyushih glavah my rassmotrim mnogo astrofizicheskih yavlenii, v kotoryh sushestvennuyu rol' igrayut i gravitaciya i elektromagnitnoe izluchenie. Budut vstrechat'sya i drugie yavleniya, gde vazhnuyu rol' igrayut krupnomasshtabnye magnitnye polya. No est' eshe odna gruppa astrofizicheskih yavlenii, gde takzhe odinakovo vazhny i gravitaciya i elektrostaticheskoe vzaimodeistvie. Rech' idet o planetah, sostoyashih iz tverdogo veshestva. V samom dele, struktura tverdyh tel, tak zhe kak i atomov i molekul, opredelyaetsya kvantovymi svoistvami zaryazhennyh mikrochastic. Ochevidno, chto svoistva planet, postroennyh iz tverdogo veshestva, dolzhny zaviset' kak ot gravitacii, tak i ot zaryadov i mass protonov i elektronov.

Soberem vse opredelyayushie parametry. Gravitacionnye svoistva harakterizuyutsya postoyannoi tyagoteniya G, massoi M i radiusom planety R. Krome togo, gravitacionnye svoistva veshestva opredelyayutsya i srednim atomnym vesom yader, kotoryi my zdes' oboznachim cherez A (tak chto massa yader ravna Am_r).

S drugoi storony, elektrostaticheskoe vzaimodeistvie elektronov i yader s uchetom kvantovyh svoistv mozhno opisat' harakternym razmerom atomov i ih energiei. Razmer atomov poryadka borovskogo radiusa a₀, a energiya takzhe poryadka energii ionizacii atoma vodoroda χ_H (sm. formuly (1.32)). Pravda, u atomov tverdyh tel, sostavlyayushih osnovnuyu massu planet, razmery v neskol'ko raz bol'she a₀, a energiya zametno men'she χ_H i eto nado uchityvat' v teh sootnosheniyah, kotorye my budem poluchat' nizhe.

Itak, imeem sleduyushii nabor opredelyayushih parametrov: G, M, R, Am_r, a₀ i χ_H. Mozhno i zdes' sostavit' matricu razmernosti, no my postupim neskol'ko inache. Planeta nahoditsya v ravnovesii, poskol'ku gravitacionnaya energiya edinicy ob'ema planety, kotoruyu mozhno nazvat' i gravitacionnym davleniem, sravnima s soprotivleniem szhatiyu so storony veshestva planety. Iz formuly (2.28) srazu sleduet dlya srednego gravitacionnogo davleniya:

$p \approx \frac{U}{\frac{4\pi}{3}R^3} \approx \frac{3}{4\pi}\frac{GM^2}{R^4}.$ (2.67)

Gravitacionnoe davlenie v central'nyh chastyah planety, ochevidno, mozhet byt' bol'she srednego v desyatki raz.

Soprotivlenie veshestva szhatiyu harakterizuetsya modulem uprugosti S, soglasno sootnosheniyu

$p = C\frac{\Delta V}{V},$ (2.68)

gde ΔV/V - otnositel'noe umen'shenie ob'ema pod deistviem davleniya r. Velichinu modulya uprugosti, imeyushuyu razmernost' erg/sm³, mozhno srazu vyrazit' cherez atomnye parametry a₀ i χ_H (sm. [6]). Imeem

$C \sim \frac{\chi_H}{a_0^3} \sim \frac{m_e^4 e^{10}}{\hbar^8}.$ (2.69)

Odnako, uchityvaya skazannoe vyshe ob istinnyh razmerah i energiyah veshestva planet, mozhno utverzhdat', chto zdes' est' chislennyi mnozhitel', zametno men'shii edinicy. V samom dele, chislennaya velichina otnosheniya

$\frac{\chi_H}{a_0^3} \approx 1,7 \cdot 10^{11} \frac{\mbox{erg}}{\mbox{sm}^3},$

to vremya kak moduli uprugosti real'nyh tverdyh tel v laboratornyh usloviyah C ≈ 10¹¹ - 10¹² erg/sm³. Pravda, v nedrah planet veshestvo szhato sil'nee, chem na poverhnosti. .Uchityvaya takzhe, chto i ΔV/V ne slishkom malo, mozhno napisat' sleduyushuyu ocenochnuyu formulu dlya davleniya veshestva planet, protivostoyashego gravitacionnomu szhatiyu:

$p \approx 10^{-1}\frac{\chi_H}{a_0^3} .$ (2.70)

Teper' sleduet priravnyat' davlenie (2.70) gravitacionnomu davleniyu v nedrah planety. Poskol'ku my poka ne mozhem ocenit' gravitacionnoe davlenie v centre planety, primem ego prosto ravnym GM²/R⁴. Togda priravnyaem etu velichinu (2.70) i nahodim:

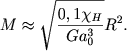
$M \approx \sqrt{\frac{0,1\chi_H}{Ga_0^3}}R^2 .$ (2.71)

Otsyuda, kstati, sleduet, chto v ramkah etoi modeli uskorenie sily tyazhesti na poverhnosti planet opredelyaetsya tol'ko universal'nymi postoyannymi:

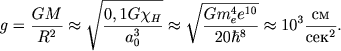
$g = \frac{GM}{R^2} \approx \sqrt{\frac{0,1G\chi_H}{a_0^3}} \approx \sqrt{\frac{Gm_e^4 e^{10}}{20\hbar^8}} \approx 10^3 \frac{\mbox{sm}}{\mbox{sek}^2}.$ (2.72)

Kak izvestno, uskorenie sily tyazhesti na poverhnosti planet zemnogo tipa (Merkurii, Venera, Zemlya, Mars, Uran, Neptun, Pluton) menyaetsya v predelah ot 360 do 1500, t. e. ne tak sil'no otlichaetsya ot (2.72). V ramkah stol' gruboi modeli mozhno schitat' neplohim soglasie, kotoroe k tomu zhe mozhno uluchshit' podborom chislennyh mnozhitelei.

Iz sootnosheniya (2.71) mozhno isklyuchit' R, esli vospol'zovat'sya opredeleniem srednei plotnosti:

$\bar\rho = \frac{3M}{4\pi R^3} \approx \frac{Am_p}{(5a_0)^3}.$ (2.73)

Zdes' Am_p - massa, prihodyashayasya na odin atom, kotoryi, po predpolozheniyu, zanimaet yacheiku razmerom 5a₀=2,5 Å. Mnozhitel' pyat' vybran tak, chtoby $\bar\rho$ iz (2.73) ne slishkom rashodilos' by s dannymi nablyudenii. Velichina A u planet zemnoi gruppy, veroyatno, okolo 50.

Isklyuchaya R iz (2.71) i (2.73), nahodim:

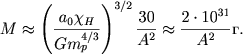
$M \approx \left(\frac{a_0\chi_H}{Gm_p^{4/3}}\right)^{3/2} \frac{30}{A^2} \approx \frac{2 \cdot 10^{31}}{A^2}\mbox{g}.$ (2.74)

Pri A ≈ 50 massa planety M ≈ 8 ⋅ 10²⁷ g, chto ne slishkom sil'no otlichaetsya ot massy Zemli - 6 ⋅ 10²⁷ g.

Takim zhe putem opredelyaetsya i radius planety. Imeem

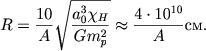
$R = \frac{10}{A}\sqrt{\frac{a_0^3\chi_H}{Gm_p^2}} \approx \frac{4 \cdot 10^{10}}{A}\mbox{sm}.$ (2.75)

Pri A = 50 poluchaem dlya radiusa planety 8 ⋅ 10³ km, chto takzhe neploho soglasuetsya s radiusom Zemli.

Analogichnye soobrazheniya byli ispol'zovany Vaiskopfom [6] dlya ocenok vysoty gor i dliny morskih voln na poverhnosti Zemli. Vysota gor opredelyaetsya iz sleduyushego usloviya: potencial'naya energiya odnoi molekuly na vershine gory ne dolzhna byt' bol'she teploty plavleniya veshestva (v raschete na odnu molekulu) u osnovaniya gory, inache ona "utonet". Potencial'naya energiya est' Am_pgH, gde H - vysota gory, a teplota plavleniya opyat' harakterizuetsya velichinoi χ_H, no s nekotorym malym mnozhitelem - po ocenke Vaiskopfa tipichnaya teplota plavleniya v raschete na odnu molekulu blizka k 10^-2χ_H. Otsyuda dlya vysoty gor imeem ocenku:

$H \approx 10^{-2} \frac{\chi_H}{Am_p g}.$ (2.76)

Esli podstavit' syuda znachenie A ≈ 50 i g ≈ 10³ sm/sek², to poluchim H ≈ 26 km. To, chto znachenie (2.76) okazalos' neskol'ko bol'she deistvitel'nogo znacheniya, legko ob'yasnit' - gory budut opuskat'sya eshe do rasplavleniya osnovaniya iz-za plastichnosti porod.

Ochevidno, chto v opredelenii radiusa planety i vysoty gor ispol'zovano odno i to zhe yavlenie - uravnoveshivanie gravitacionnogo prityazheniya soprotivleniem veshestva szhatiyu ili rasplavleniyu, obyazannomu elektrostaticheskim silam v atomah i molekulah. Poetomu R iz (2.75) i H iz (2.76) odinakovym obrazom zavisyat ot universal'nyh konstant; razlichie lish' v chislennyh mnozhitelyah, opisyvayushih, s odnoi storony, szhatie veshestva pri ochen' vysokih davleniyah, a s drugoi storony, - ego rasplavlenie ili plastichnost' pri bolee umerennyh davleniyah. Esli podstavit' v (2.76) vyrazhenie (2.72) i schitat', chto atomnye vesa gornyh porod i nedr Zemli sravnimy, to poluchim H ≈ 3 ⋅ 10^-3R.

Veroyatno, formula (2.76) imeet bol'shuyu oblast' primenimosti - pri ee vyvode ne ispol'zovalis' neskol'ko neopredelennye dannye o davlenii v nedrah planet i o svoistvah veshestva. Chislennyi mnozhitel' v (2.70) ocenen ochen' grubo. Vozmozhno, chto on sushestvennym obrazom zavisit ot sostoyaniya veshestva i poetomu mozhet byt' razlichen u raznyh planet. V (2.76) eta neopredelennost' slabee i poetomu formulu (2.76) mozhno ispol'zovat' i dlya ocenki vysoty gor na planetah s raznymi usloviyami. Rassmotrim, naprimer, planety s odinakovoi srednei plotnost'yu. Togda uskorenie sily tyazhesti na poverhnosti etih planet

$g = \frac{GM}{R^2}. = \frac{4\pi}{3}G\bar\rho R.$ (2.77)

Podstavlyaya (2.77) v (2.76), nahodim

$HR \approx 2,5 \cdot 10^{-3} \frac{\chi_H}{Am_pG\bar\rho} \approx 4,9 \cdot 10^5 \mbox{km}^2,$ (2.78)

esli prinyat' A ≈ 50 i $\bar\rho$ &assymp 2 g/sm³. Otsyuda sleduet, chto perestayut byt' sfericheskimi planety s razmerom men'shim 700 km, t. e. malye planety Solnechnoi sistemy. Vozmozhno, chto sootnoshenie (2.78) opredelyaet i verhnii predel razmerov oskolkov pri razrushenii planet.

Dlya opredeleniya dlin voln (λ) na poverhnosti morya Vaiskopf [6] ispol'zoval sleduyushie soobrazheniya. Veter vozbuzhdaet v pervuyu ochered' volny s naimen'shei fazovoi skorost'yu, a togda λ na poverhnosti morya opredelyaetsya poverhnostnym natyazheniem σ . Imeem

$\lambda \approx \sqrt{\frac{\sigma}{g\rho}}.$ (2.79)

Poverhnostnoe natyazhenie est' energiya na edinicu ploshadi, t. e. v atomnyh velichinah v $\sigma \sim \frac{\chi_H}{a_0^2}$ . Prinimaya zdes' takzhe $\rho \sim \frac{m_p}{a_0^3}$ , poluchim

$\lambda^2 \approx 3 \cdot 10^{-3} \frac{a_0\chi_H}{m_pg},$ (2.80)

gde chislennyi mnozhitel' sootvetstvuet volnam na poverhnosti vody.

Itak, kak podcherkivaet Vaiskopf [6], dazhe dlina morskih voln est' sledstvie "sorevnovaniya" mezhdu gravitacionnym vzaimodeistviem i atomnymi elektrostaticheskimi silami.

<< § 2.2 Vzaimodeistvie elektromagnitnogo izlucheniya i veshestva | Oglavlenie | § 3.1 Sootnoshenie massa — svetimost' >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce