Glava III. Osnovnye harakteristiki zvezd

Zvezdy - eto, po-vidimomu, naibolee rasprostranennye vo Vselennoi kosmicheskie tela, imeyushie vmeste s tem otnositel'no prostuyu strukturu. So vremeni pervyh astrofizicheskih nablyudenii nashi znaniya o zvezdah postoyanno uvelichivayutsya, prichem otkrytiya poslednih let vse vremya prinosyat neozhidannosti; dostatochno vspomnit' radiopul'sary i rentgenovskie istochniki v dvoinyh sistemah. Odnako vse zhe prinyato schitat', chto glavnye zakony, opisyvayushie zvezdnuyu fiziku, izvestny dostatochno nadezhno, hotya neopredelennyi rezul'tat eksperimenta s solnechnymi neitrino vnosit nekotorye somneniya. V etoi glave my pokazhem, chto osnovnye sootnosheniya, svyazyvayushie mezhdu soboi parametry zvezd, mogut byt' vyvedeny s pomosh'yu prostyh soobrazhenii razmernosti. Bolee strogoe rassmotrenie zvezdnyh modelei s tochki zreniya ih podobiya budet dano v gl. 4

§ 3.1 Sootnoshenie massa — svetimost'

V pervuyu ochered' zaimemsya poiskom zavisimostei mezhdu harakteristikami zvezdy. Osnovnyh parametrov tri: eto massa M, radius R i svetimost' L. V uravnenie sostoyaniya veshestva zvezdy vhodyat universal'naya gazovaya postoyannaya ℜ i bezrazmernyi molekulyarnyi ves μ. Kak pravilo, struktura zvezdy, v pervuyu ochered' ee termodinamicheskie harakteristiki, opredelyaetsya perenosom energii, generiruemoi v ee central'nyh chastyah, cherez vsyu ee tolshu. Naibol'shuyu rol' igraet perenos energii izlucheniem, kotoryi mozhno harakterizovat' dvumya opredelyayushimi parametrami - universal'noi konstantoi σ (postoyannoi zakona Stefana-Bol'cmana) i koefficientom poglosheniya ϰ , harakterizuyushim "prosachivanie" izlucheniya skvoz' veshestvo. Budem otnosit' ϰ k edinice plotnosti.

Razmernosti opredelyayushih parametrov takovy:

$\begin{array}{l} \quad [M] = \mbox{g}, \quad [R] = \mbox{sm}, \quad [L] = \frac{\mbox{g} \cdot \mbox{sm}^2}{\mbox{sek}^3}, \quad [G] = \frac{\mbox{sm}^3}{\mbox{g} \cdot \mbox{sm}^2}, \\ \\ \quad [\frac{\mathfrak {R}}{\mu}] = \frac{\mbox{sm}^2}{\mbox{sek}^2 \cdot \mbox{grad}}, \quad [\sigma] = \frac{\mbox{erg}}{\mbox{sek} \cdot \mbox{sm}^2 \cdot \mbox{grad}^4} = \frac{\mbox{g}}{\mbox{sek}^3 \cdot \mbox{grad}^4}, \\ \\ \quad [\varkappa] = \frac{1}{\mbox{sm}} \cdot \frac{\mbox{sm}^3}{\mbox{g}} = \frac{\mbox{sm}^2}{\mbox{g}}. \end{array}$ (3.1)

Etu sistemu mozhno uprostit'. Razmernost' temperatury (gradus) vhodit tol'ko v dva parametra - ℜ/μ i σ . Ochevidno, chto vo vse bezrazmernye kompleksy mozhet vhodit' tol'ko takaya kombinaciya etih dvuh parametrov, v kotoroi razmernost' gradusa sokrashaetsya, a imenno:

$[\frac{\sigma \mu^4}{\mathfrak {R}^4}] = \frac{\mbox{g} \cdot \mbox{sek}^5}{\mbox{sm}^8}.$ (3.2)

Teper' ostaetsya shest' opredelyayushih parametrov s tremya nezavisimymi razmernostyami. Sostavim matricu razmernosti:

$\begin{matrix} \, & [M] & [L] & [R] & [G] & [\varkappa] & [\frac{\sigma \mu^4}{\mathfrak {R}^4}] \\ \mbox{g}&1&1&0&-1&-1&1 \\ \mbox{sm}&0&2&1&3&2&8 \\ \mbox{sek}&0&-3&0&-2&0&5 \\ \end{matrix}$ (3.3)

Rang matricy raven trem. Opredelyaya bezrazmernyi kompleks proizvedeniem

$\Pi = M^{k_1}L^{k_2}R^{k_3}G^{k_4}\varkappa^{k_5}\left(\frac{\sigma \mu^4}{\mathfrak {R}^4}\right)^{k_6},$ (3.4)

poluchaem sistemu uravnenii dlya pokazatelei k_i:

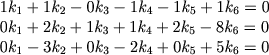
$\begin{array}{l} 1k_1 + 1k_2 - 0k_3 - 1k_4 - 1k_5 + 1k_6 = 0\\ 0k_1 + 2k_2 + 1k_3 + 1k_4 + 2k_5 - 8k_6 = 0 \\ 0k_1 - 3k_2 + 0k_3 - 2k_4 + 0k_5 + 5k_6 = 0 \end{array}$ (3.5)

imeyushuyu tri lineino nezavisimyh resheniya. Vyberem ih tak, chtoby kazhdyi bezrazmernyi kompleks ne vklyuchal by v sebya po ocheredi osnovnye parametry R, L i ϰ . Krome togo, pri etom budem uchityvat' nekotorye fizicheskie soobrazheniya, kotorye stanut yasnymi nizhe.

Pervyi bezrazmernyi kompleks vyberem tak, chtoby tuda ne vhodil radius zvezdy (prinimaya k₃ = 0). Dlya svetimosti primem pokazatel' k₂ = 1. Ostaetsya eshe odin proizvol'nyi parametr, kotoryi vyberem tak: k₆ = - 1. Togda imeem pervyi kompleks:

$\Pi_1 = LM^{-3}G^{-4} \frac{\mathfrak {R}^4}{\sigma \mu^4},$ (3.6)

Vo vtorom bezrazmernom komplekse opustim svetimost' (k₂ = 0), a zaodno i chlen, opisyvayushii potok izlucheniya (k₆ = 0). Polozhim takzhe k₁ = - 1. Togda imeem

$\Pi_2 = R^2 M^{-1}\varkappa^{-1} = \frac{3}{4\pi}(\varkappa\bar\rho R)^{-1}.$ (3.7)

gde $\bar\rho = \frac{3M}{4\pi R^3}$ .

V tret'em bezrazmernom komplekse opustim koefficient neprozrachnosti (k₅). Zdes' mozhno takzhe opustit' termodinamicheskie parametry (k₆ = 0) i polozhit' k₂=1. Imeem

$\Pi_3 = LR^{5/2} G^{-3/2} M^{-5/2}.$ (3.8)

Itak, my poluchili tri bezrazmernyh kompleksa, i iskomoe sootnoshenie, teper' imeyushee vid ƒ(P₁, P₂, P₃) = 0, po-prezhnemu ostaetsya neopredelennym do teh por, poka my ne ocenim poryadki velichin P₁, P₂, P₃. Parametr P₂ imeet ochevidnyi smysl - eto est' velichina, obratnaya opticheskoi tolshe zvezdy, otnesennoi k ee srednei plotnosti. Dlya vseh real'nyh zvezd velichina etogo kompleksa na mnogo poryadkov men'she edinicy. Poetomu v dal'neishem vsegda P₂ mozhno prenebrech'.

Fizicheskii smysl tret'ego bezrazmernogo kompleksa takzhe neslozhen. Perepishem (3.8) v vide

$\Pi_3 = L \left[\frac{GM^2}{R} \cdot \sqrt{\frac{GM}{R^3}}\right]^{-1}.$ (3.9)

Soglasno (2.28) GM²/R est' po poryadku velichiny polnaya energiya zvezdy, a soglasno (2.9) ili (2.13) parametr (R³/GM)^1/2 harakterizuet period kolebaniya zvezdy ili vremya ee szhatiya v sluchae neustoichivosti. Takim obrazom, bezrazmernyi kompleks P₃ byl by poryadka edinicy lish' v tom sluchae, esli by zvezda izluchala svoyu polnuyu energiyu za vremya poryadka perioda kolebanii ili polnogo szhatiya. Dlya nekotoryh bystryh etapov obrazovaniya i evolyucii zvezd eto uslovie deistvitel'no imeet mesto, no dlya stacionarnyh zvezd bezrazmernyi kompleks P₃ takzhe na mnogo poryadkov men'she edinicy.

Ostaetsya kompleks P₁ (3.6). Chtoby sudit' o nem, ocenim prezhde vsego ego velichinu dlya Solnca. Poluchim

$\Pi_1 \approx 0,03\mu^{-4}\{\varkappa\},$ (3.10)

gde, napominaem, {ϰ} oznachaet chislennoe znachenie velichiny koefficienta neprozrachnosti.

Srednee znachenie koefficienta neprozrachnosti, rasschitannoe dlya sovremennyh modelei Solnca, poryadka ili neskol'ko bol'she edinicy sm² ⋅ g^-1, a velichina molekulyarnogo vesa blizka k 0,6, poetomu chislennoe znachenie mnozhitelya P₁ poryadka 2-3. Itak, kompleks P₁ deistvitel'no po poryadku velichiny blizok k edinice.

Ego fizicheskii smysl zaklyuchaetsya v sleduyushem. Stacionarnye zvezdy sushestvuyut tol'ko blagodarya tomu, chto gravitacionnoe prityazhenie kompensiruetsya gazovym davleniem, dlya kotorogo neobhodima vysokaya temperatura gaza. V svoyu ochered' temperatura veshestva zvezdy opredelyaetsya ne tol'ko usloviyami generacii energii, no i usloviem "prosachivaniya" etoi energii cherez tolshu zvezdy. Zdes' dolzhno imet' mesto nekotoroe samosoglasovanie - v zvezde dannoi massy dolzhno generirovat'sya stol'ko energii, skol'ko ee mozhet "prosochit'sya" k poverhnosti. Otsyuda i odnoznachnaya svyaz' mezhdu svetimost'yu, massoi i koefficientom neprozrachnosti. Eta svyaz', obnaruzhennaya vpervye i teoreticheski, i po dannym nablyudenii A. Eddingtonom eshe v 1921 g., nazyvaetsya sootnosheniem massa - svetimost' i yavlyaetsya odnoi iz vazhneishih astrofizicheskih zakonomernostei. Privedennyi vyshe elementarnyi vyvod na osnove soobrazhenii analiza razmernostei pozvolyaet sootnoshenie massa - svetimost' zapisat' v vide

$\frac{L}{L_{\odot}} \approx \frac{30\mu^4}{\{\varkappa\}}\left(\frac{M}{M_{\odot}}\right)^3.$ (3.11)

Formula (3.11) udovletvoritel'no opisyvaet svetimost' Solnca i daet, po krainei mere kachestvennoe, soglasie s nablyudaemoi zavisimost'yu massa - svetimost'. Kolichestvennye rashozhdeniya s nablyudaemoi zavisimost'yu, odnako, dostatochno zametny. Prichin dlya etogo neskol'ko. Pri vyvode etoi formuly predpolagaetsya, chto koefficient neprozrachnosti postoyanen po vsei zvezde i odinakov u zvezd raznyh mass. Na samom dele eto vypolnyaetsya tol'ko v tom sluchae, esli neprozrachnost' ob'yasnyaetsya tomsonovskim rasseyaniem. Togda, deistvitel'no, L ∼ M³. Drugie mehanizmy poglosheniya sveta privodyat k sushestvennoi zavisimosti ϰ ot plotnosti i osobenno ot temperatury. Eto privodit k bolee slozhnoi zavisimosti svetimosti ot massy, kotoraya budet poluchena v sleduyushei glave.

Krome togo, sootnoshenie massa - svetimost' zavisit, hotya i slabee, ot zakona vydeleniya energii. Tem ne menee formula (3.11) sohranyaet svoe metodicheskoe znachenie prezhde vsego v silu svoei elementarnosti. Ee obsuzhdenie pozvolyaet prosto ob'yasnit' mnogie yavleniya fiziki zvezd (sm. izlozhenie v [1]).

<< § 2.3 Harakternye parametry tverdyh planet | Oglavlenie | § 3.2 Ravsnovesie i ustoichivost' zvezd >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce