Astronet > Razmernosti i podobie astrofizicheskih velichin

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 3.2 Ravsnovesie i ustoichivost' zvezd | Oglavlenie | § 3.4 Harakternye vremena otdel'nyh etapov evolyucii zvezd >>

§ 3.3 Belye karliki, neitronnye zvezdy i "chernye dyry"

Drugim primerom zvezd s odnoznachnoi zavisimost'yu davleniya ot plotnosti yavlyayutsya zvezdy, sostoyashie iz vyrozhdennogo gaza. Eti zvezdy takzhe udobno izuchat' metodom teorii razmernostei.

Napomnim fiziku etogo yavleniya. Rassmotrim gaz iz svobodnyh elektronov. (V silu principa Pauli v odnom kvantovomehanicheskom sostoyanii (bez ucheta spina), t.e. v odnoi kvantovoi yacheike fazovogo prostranstva, mozhet nahodit'sya ne bolee dvuh elektronov. Pri bol'shoi prostranstvennoi plotnosti elektronov na odin elektron prihoditsya malyi geometricheskii ob'em i, sledovatel'no, bol'shoi ob'em prostranstva impul'sov. Inymi slovami, pri bol'shoi plotnosti impul'sy svobodnyh elektronov dolzhny byt' veliki, dazhe esli ih temperatura ravna nulyu. Gaz svobodnyh elektronov pri bol'shih ih koncentraciyah n_e, imeet vysokoe davlenie i pri T = 0. Yasno, chto eto davlenie vyrozhdennogo elektronnogo gaza mozhet protivostoyat' sile tyagoteniya i tem samym obespechit' sushestvovanie osobogo tipa zvezd. Takie zvezdy deistvitel'no byli otkryty bolee 50 let nazad i ih nazyvayut belymi karlikami (ili "chernymi" karlikami, esli u nih T → 0).

Uravneniya sostoyaniya vyrozhdennogo elektronnogo gaza vyvodyatsya v ramkah kvantovoi statisticheskoi fiziki i ego mozhno naiti vo mnogih uchebnikah. No okazyvaetsya, chto eti zhe uravneniya mogut byt' polucheny elementarneishim obrazom metodom teorii analiza razmernostei bez ispol'zovaniya slozhnogo apparata kvantovoi mehaniki.

Zapishem opredelyayushie parametry zadachi. Dva iz nih ochevidny - davlenie p i elektronnaya koncentraciya n_e. Poskol'ku samo yavlenie vyrozhdeniya elektronnogo gaza svyazano s kvantovymi svoistvami, to v chislo opredelyayushih parametrov dolzhna vhodit' postoyannaya Planka ħ. Pri bol'shih plotnostyah elektrony mogut stat' relyativistskimi - uchtem v opredelyayushih parametrah i skorost' sveta c. Sam elektron harakterizuetsya massoi m_e i zaryadom e, no esli kulonovskim ottalkivaniem mezhdu elektronami mozhno prenebrech', to ostanetsya lish' parametr m_e. Temperaturu gaza budem schitat' ravnoi nulyu, a sledovatel'no, i davleniem ionnoi komponenty takzhe mozhno prenebrech'.

Sostavim matricu razmernosti dlya privedennyh vyshe parametrov:

$\begin{matrix} \, & [p] & [n_e] & [\hbar] & [c] & [m_e] \\ \mbox{g}&1&0&1&1&1 \\ \mbox{sm}&-1&-3&2&1&0 \\ \mbox{sek}&-2&0&-1&-1&0\\ \end{matrix}$

Rang matricy raven trem i, sledovatel'no, zdes' est' dva nezavisimyh bezrazmernyh kompleksa. Vyberem ih tak, chtoby v odin iz nih byla by vklyuchena massa m_e, no opushena skorost' sveta c, a v drugom, naoborot, sohranena c, no opushena m_e. Poluchim

$\Pi_1 = pm_e\hbar^{-2}n_e^{-5/3} ;$ (3.36)

$\Pi_2 = p\hbar^{-1}c^{-1}n_e^{-4/3} .$ (3.37)

Poskol'ku imeyutsya dva bezrazmernyh kompleksa, to polnoe uravnenie sostoyaniya vyrozhdennogo elektronnogo gaza pri nulevoi temperature mozhno zapisat' kak

$f(\Pi_1, \Pi_2) = 0,$ (3.38)

gde funkciya ƒ(P₁, P₂) iz soobrazhenii analiza razmernostei ne opredelyaetsya. Tochnoe vychislenie na osnove kvantovoi mehaniki s uchetom effektov teorii otnositel'nosti daet sleduyushee slozhnoe vyrazhenie:

$y - \frac{\arcsin x}{x^4} - \frac{(2x^2 - 3)\sqrt{x^2 +1}}{3x^3} = 0,$ (3.39)

gde cherez h i u oboznacheny sleduyushie kombinacii:

$x = \sqrt[3]{3\pi^2}\frac{\Pi_2}{\Pi_1}, \quad y = \frac{8\pi^2\Pi_2}{3(3\pi^2)^{\frac{4}{3}}}.$ (3.40)

Uravnenie sostoyaniya (3.39) - (3.40) - polnoe, uchityvayushee kak relyativistskie, tak i nerelyativistskie elektrony. V predel'nyh sluchayah otnositel'no nebol'shoi ili ochen' bol'shoi elektronnoi koncentracii mozhno poluchit' uravnenie sostoyaniya i ne pribegaya k opredeleniyu funkcii (3.38).

V sluchae otnositel'no maloi koncentracii elektronov dazhe naibolee bystrye iz nih imeyut skorosti, sushestvenno men'shie, chem skorost' sveta. Inymi slovami, v etom sluchae s ne yavlyaetsya opredelyayushim parametrom ili, chto odno i to zhe, mozhno schitat' P₂ << 1.

Iz soobrazhenii analiza razmernostei sleduet, chto v sluchae nerelyativistskogo vyrozhdennogo elektronnogo gaza uravnenie sostoyaniya opredelyaetsya formuloi (3.36) pri P₁=const. Kvantovaya mehanika daet znachenie P₁ kotoroe mozhno takzhe poluchit' iz (3.39) i (3.40), esli pereiti k predelu P₂ → 0. V rezul'tate poluchaem

$p = \frac{(3\pi^2)^{2/3}}{5}\frac{\hbar^2}{m_e}n_e^{5/3},$ (3.41)

t.e. P₁ = 1,95.

V sluchae ochen' bol'shoi elektronnoi plotnosti skorosti bol'shei chasti elektronov blizki k skorosti sveta i P₂ ne maló . No zato v etom sluchae mozhno prenebrech' kompleksom P₁. V samom dele, massa pokoya relyativistskih chastic sushestvennogo znacheniya ne imeet i, po sushestvu, m_e ne est' opredelyayushii parametr. Schitan P₁ << 1, iz soobrazhenii teorii analiza razmernostei poluchaem uravnenie sostoyaniya (3.37) pri P₂ = const. S uchetom chislennogo mnozhitelya, kotoryi mozhno poluchit' i iz (3.39) pri razlozhenii po P₁ << 1, imeem uravnenie sostoyaniya relyativistskogo vyrozhdennogo elektronnogo gaza:

$p = \frac{(3\pi^2)^{1/3}}{4}\hbar cn_e^{4/3}.$ (3.42)

V etom sluchae bezrazmernyi kompleks P₂ = 0,78 - t. e. tozhe ochen' blizok k edinice. Poetomu, dazhe sovsem ne ispol'zuya kvantovuyu mehaniku (t. e. ne znaya chislennyh znachenii P₁ i P₂), mozhno poluchit' uravnenie sostoyaniya s bol'shoi tochnost'yu tol'ko iz odnih soobrazhenii teorii analiza razmernostei.

Esli vklyuchit' v chislo opredelyayushih parametrov i temperaturu, to mozhno poluchit' kriterii vyrozhdeniya. Bolee polnye uravneniya s uchetom temperaturnyh effektov sostoyaniya budut privedeny v sleduyushei glave.

Veshestvo v celom dolzhno byt' elektricheski neitral'no. Poetomu koncentraciya elektronov opredelyaet i koncentraciyu tyazhelyh chastic. Oboznachim cherez re molekulyarnyi ves tyazhelyh chastic, prihodyashihsya na odin elektron. U belyh karlikov razlichnogo himicheskogo sostava velichina μ_e obychno lish' nemnogo prevyshaet dvoiku. Otsyuda dlya plotnosti veshestva belyh karlikov imeem

$\rho = n_e m_p \mu_e,$ (3.43)

gde m_p - massa protona. Teper' oba uravneniya sostoyaniya primut vid

$p = \frac{(3\pi^2)^{\frac{2}{3}}}{5}\frac{\hbar^2}{m_e} \left(\frac{\rho}{\mu_e m_p}\right)^{\frac{5}{3}} = K_{5/3}\rho^{5/3}$ (3.44)

dlya nerelyativistskogo gaza, i

$p = \frac{(3\pi^2)^{\frac{1}{3}}}{4} \hbar c \left(\frac{\rho}{\mu_e m_p}\right)^{\frac{4}{3}} = K_{4/3}\rho^{4/3}$ (3.45)

dlya relyativistskogo elektronnogo gaza. (V oboih predel'nyh sluchayah my poluchim politropnye sootnosheniya s pokazatelyami γ = 5/3 i γ = 4/3 sootvetstvenno.

Privedennyi zdes' vyvod uravnenii sostoyaniya vyrozhdennogo elektronnogo gaza naglyadno illyustriruet vozmozhnosti metoda analiza razmernostei. Ispol'zuya sootnosheniya (3.44) i (3.45), mozhno teper' ocenit' parametry belyh karlikov. V sluchae zvezd maloi massy, kogda dazhe v centre belyh karlikov net relyativistskih elektronov, mozhno ispol'zovat' dlya davleniya formulu (3.44). Tak kak zdes' γ = 5/3, to iz (3.17) sleduet dlya radiusa zvezdy:

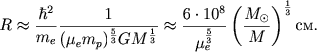
$R \approx \frac{\hbar^2}{m_e} \frac{1}{(\mu_e m_p)^{\frac{5}{3}} GM^{\frac{1}{3}}} \approx \frac{6 \cdot 10^8}{\mu_e^{\frac{5}{3}}} \left(\frac{M_{\odot}}{M}\right)^{\frac{1}{3}} \mbox{sm}.$ (3.46)

Zdes' opusheny chislennye mnozhiteli, kotorye bolee tochno budut opredeleny v sleduyushei glave.

Formula (3.46) spravedliva lish' dlya zvezd malyh mass (M < 0,5 M_☉). S uvelicheniem massy uvelichivaetsya i central'naya plotnost' belyh karlikov (umen'shaetsya radius). Iz-za etogo v ih centrah uvelichivaetsya stepen' relyativizacii i nado postepenno perehodit' k uravneniyu sostoyaniya (3.45), tochnee, nado stroit' modeli s polnym uravneniem sostoyaniya (3.39) - (3.40).

Odnako v predele naibol'shih plotnostei pochti dlya vsei massy belogo karlika spravedlivo uravnenie sostoyaniya (3.45) i takoi belyi karlik opisyvaetsya politropoi s γ = 4/3. Iz (3.19) sleduet, chto u podobnoi zvezdy fiksirovana lish' massa. Soglasno (3.19), opuskaya mnozhiteli poryadka edinicy, imeem

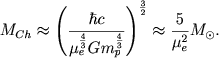
$M_{Ch} \approx \left(\frac{\hbar c}{\mu_e^{\frac{4}{3}}G m_p^{\frac{4}{3}}}\right)^{\frac{3}{2}} \approx \frac{5}{\mu_e^2}M_{\odot}.$ (3.47)

Velichina (3.47) (ee tochnoe vyrazhenie budet privedeno v gl. 4) nazyvaetsya chandrasekarovskim predelom. Massa belyh karlikov ne mozhet byt' bol'she etoi velichiny.

Radius politropy s γ = 4/3 ne opredelen. No poskol'ku elektronnyi gaz v belyh karlikah dazhe s ochen' bol'shoi central'noi plotnost'yu vse zhe ostaetsya nerelyativistskim v ego poverhnostnyh sloyah, to zdes' net "chistoi" politropy γ = 4/3. Srednee "effektivnoe" γ nemnogo bol'she i poetomu sohranyaetsya zavisimost' - umen'shenie (radiusa s uvelicheniem massy. Eto oznachaet, chto po mere priblizheniya massy belogo karlika k chandraoekarovskomu predelu ego radius umen'shaetsya i stremitsya k nulyu po mere dostizheniya etogo predela. Raschety s uravneniem sostoyaniya (3.39) - (3.40) podtverzhdayut etot vyvod (sm. podrobnee [3]).

Vazhnoi osobennost'yu zvezd tipa belyh karlikov yavlyaetsya odnoznachnaya zavisimost' mezhdu ego radiusom, massoi i elektronnym molekulyarnym vesom, kotoraya legko vidna uzhe iz (3.46). Elektronnyi molekulyarnyi ves menyaetsya v nebol'shih predelah, i u vseh belyh karlikov dolzhen byt' blizok k dvum. Poetomu v pervom priblizhenii radius belogo karlika bolee ili menee odnoznachno opredelyaetsya ego massoi. Etot teoreticheskii vyvod v principe mozhno ispol'zovat' dlya opredeleniya mass belyh karlikov. Naprimer, gravitacionnoe krasnoe smeshenie v spektrah belyh karlikov,

$\frac{\Delta\nu}{\nu} = \frac{2GM}{c^2 R} \sim M^{4/3},$ (3.48)

Ne sovsem yasen vklad atmosfery belogo karlika, net uverennogo metoda vydeleniya gravitacionnoi chasti iz obshego smesheniya spektral'nyh linii i t. p. Po-prezhnemu massy belyh karlikov opredelyayutsya pochti isklyuchitel'no po ih orbital'nomu dvizheniyu v dvoinyh sistemah, a izmerenie gravitacionnogo krasnogo smesheniya ispol'zuetsya lish' dlya sopostavleniya s teoreticheskoi zavisimost'yu mezhdu M i R. Nablyudatel'nyi material ochen' nebogat, no kachestvennoe soglasie teorii i nablyudenii imeetsya.

Bolee podrobno teoriyu belyh karlikov my budem obsuzhdat' v sleduyushei glave. Pri ochen' bol'shih plotnostyah stanovitsya neustoichivym sostoyanie gaza, v kotorom imeyutsya atomnye yadra i vyrozhdennye elektrony. Zdes' elektrony kak by "vdavlivayutsya" v yadra, prevrashaya protony v neitrony. Yadra raspadayutsya, v veshestve poyavlyaetsya primes' svobodnyh neitronov, a pri eshe bol'shih plotnostyah veshestvo prevrashaetsya v neitronnyi gaz.

Neitronnyi gaz takzhe okazyvaetsya vyrozhdennym. Sostoyashie iz takogo veshestva zvezdy i est' neitronnye zvezdy, stavshie v poslednee vremya ochen' populyarnymi v svyazi s otkrytiem pul'sarov i rentgenovskih istochnikov. Raschety modelei neitronnyh zvezd provodilis' neodnokratno. Trudnosti zdes' v tom, chto neizvestno bolee ili menee tochnoe uravnenie sostoyaniya neitronnogo gaza.

No dlya prostyh ocenok my mozhem ispol'zovat' uzhe izvestnye sootnosheniya. Formuly, poluchennye vyshe iz soobrazhenii analiza razmernostei, spravedlivy, razumeetsya, i v tom sluchae, esli my vmesto elektronov budem ponimat' neitrony. Vsya raznica v tom, chto m_e i m_p sleduet zamenit' na m_n - massu neitrona, a μ_e schitat' ravnoi edinice.

Uravnenie sostoyaniya nerelyativistskogo vyrozhdennogo neitronnogo gaza est'

$p \approx \frac{\hbar^2}{m_n} n_n^{\frac{5}{3}} \approx \frac{\hbar^2}{m_n^{\frac{8}{3}}} \rho^{\frac{5}{3}},$ (3.49)

gde n_n - koncentraciya neitronov. Chislennogo mnozhitelya zdes' net iz-za otsutstviya tochnoi teorii.

Dlya relyativistskogo vyrozhdennogo neitronnogo gaza

$p \approx \hbar c n_n^{4/3}.$ (3.50)

U neitronnoi zvezdy, sostoyashei iz nerelyativistskogo vyrozhdennogo neitronnogo gaza, takzhe est' odnoznachnaya zavisimost' mezhdu massoi i radiusom, analogichnaya (3.46):

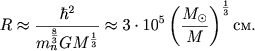
$R \approx \frac{\hbar^2}{m_n^{\frac{8}{3}}GM^{\frac{1}{3}}} \approx 3 \cdot 10^5 \left(\frac{M_{\odot}}{M}\right)^{\frac{1}{3}} \mbox{sm}.$ (3.51)

S tochnost'yu do chislennyh mnozhitelei, kotorye mozhno poluchit' tol'ko iz tochnoi teorii, radius neitronnoi zvezdy men'she radiusa belogo karlika na mnozhitel', ravnyi otnosheniyu massy elektrona k masse neitrona.

S uvelicheniem massy zvezdy plotnost' neitronnogo gaza uvelichivaetsya i on stanovitsya relyativistskim. Proishodit priblizhenie k politrope γ = 4/3, v rezul'tate chego i neitronnye zvezdy imeyut predel massy (predel Oppengeimera - Volkova), po poryadku velichiny blizkii k (3.47):

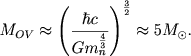
$M_{OV} \approx \left(\frac{\hbar c}{G m_n^{\frac{4}{3}}}\right)^{\frac{3}{2}} \approx 5M_{\odot}.$ (3.52)

Na samom dele chislennoe znachenie nedostatochno tochno, poskol'ku zdes' est' eshe mnozhiteli poryadka edinicy, tochnoe znachenie kotoryh poka ne izvestno. Razlichnye modeli dayut dlya verhnego predela massy neitronnyh zvezd velichinu okolo 2-3 mass Solnca.

Mozhno poluchit' eshe odin sposob ocenki verhnego predela massy stacionarnyh neitronnyh zvezd. Radius lyubogo stacionarnogo tela dolzhen byt' bol'she ego gravitacionnogo radiusa R_g=2GM/c². Uchityvaya (3.51), imeem

$\frac{\hbar^2}{m_n^{\frac{8}{3}}GM^{\frac{1}{3}}} > \frac{2GM}{c^2}.$ (3.53)

Otsyuda, s tochnost'yu do mnozhitelya 2^-4/3, takzhe sleduet predel (3.52).

Radius neitronnyh zvezd obychno vsego v neskol'ko raz prevyshaet ih gravitacionnyi radius, poetomu effekt obshei teorii otnositel'nosti ves'ma sushestven. Eshe vazhnee on dlya zvezd s massoi, bol'shei predela (3.52). V etom sluchae nikakoe davlenie veshestva ne v sostoyanii protivostoyat' sile gravitacionnogo prityazheniya i podobnye zvezdy dolzhny szhimat'sya, uhodya pod svoyu "poverhnost' Shvarcshil'da" - sferu s radiusom, ravnym gravitacionnomu radiusu. Obrazuyutsya tak nazyvaemye "chernye dyry" ili "zastyvshie zvezdy". Sobstvennoe izluchenie s poverhnosti etih zvezd ne vyhodit, no oni blagodarya svoemu moshnomu gravitacionnomu polyu prityagivayut veshestvo (akkreciya), kotoroe pri padenii na podobnoe telo razogrevaetsya i izluchaet v rentgenovskom diapazone (sm. gl. 2).

Moshnost' izlucheniya mozhno opredelit' po skorosti akkrecii, dlya kotoroi sootvetstvuyushie formuly byli polucheny iz soobrazhenii analiza razmernostei (sm. (2.30) - (2.31)). Naibol'shii razogrev i, sledovatel'no, naibol'shaya moshnost' izlucheniya akkreciruyushego gaza idet iz oblasti, okruzhayushei "chernuyu dyru" primerno na rasstoyanii treh gravitacionnyh radiusov. Nado takzhe imet' v vidu, chto chasto eta akkreciya imeet nesimmetrichnyi harakter. V teh sluchayah, kogda "chernaya dyra" vhodit v sostav tesnoi dvoinoi sistemy (zdes' obychno akkreciya naibol'shaya), gaz, prityagivaemyi k "chernoi dyre", obrazuet snachala disk i tol'ko potom vypadaet na "dyru". Vliyaet na akkreciyu i magnitnoe pole. Dlya gruboi ocenki mozhno schitat', chto "ploshad' akkrecii" poryadka $R_g^2$ . Poskol'ku na rasstoyanii 3R_g skorost' dvizheniya okolo $1/\sqrt{3}$ skorosti sveta, to energiya, vydelyaemaya pri akkrecii gaza za edinicu vremeni,

$L \approx \frac{c^2}{10}\frac{dM}{dt} \approx \frac{2\pi c^2 (GM)^2 \rho}{10 v^3} \approx \frac{1}{2}R_g^2\rho c^3,$ (3.54)

gde ρ - plotnost' akkreciruyushego veshestva vblizi tela; prinyato takzhe $v \approx c/\sqrt{3}$ . No svetimost' lyubogo ob'ekta ne mozhet byt' bol'she eddingtonovskogo predela (3.34) - (3.45), kotoryi mozhno zapisat' v vide

$L \lesssim \frac{m_p c^3}{r_0^2}R_g,$ (3.55)

gde, napominaem, r₀ est' klassicheskii radius elektrona. Otsyuda stacionarnaya akkreciya vozmozhna lish' pri

$\rho \lesssim \frac{2m_p}{r_0^2 R_g} \lesssim 2 \cdot 10^4 \frac{M_\odot}{M}\frac{\mbox{g}}{\mbox{sm}^3}.$ (3.56)

Legko ubedit'sya, chto moshnoe izluchenie pri akkrecii na "chernye dyry" sosredotocheno v rentgenovskom diapazone. V samom dele, potok izlucheniya s edinicy poverhnosti raven

$\frac{L}{4\pi R^2} \lesssim \frac{m_p c^3}{4\pi r_0^2} \frac{R_g}{R^2} \approx 10^{-2} \frac{m_p c^3}{r_0^2 R_g}.$ (3.57)

Zdes' predpolagaetsya, chto izluchenie idet s poverhnosti, radius kotoroi v tri raza bol'she gravitacionnogo radiusa. Yarkostnaya temperatura etogo izlucheniya

$T \approx \sqrt[4]{\frac{L}{4\pi R^2 \sigma}} \approx \frac{1}{3}\sqrt[4]{\frac{m_p c^3}{r_0^2 R_g}} \approx 10^7 \mbox{grad},$ (3.58)

chto i sootvetstvuet rentgenovskomu diapazonu (dlina volny λ ≈ 1 - 10 Å). Rentgenovskie istochniki v tesnyh dvoinyh sistemah, gde mozhno ozhidat' sushestvennoi akkrecii za schet peretekaniya veshestva ot odnoi zvezdy k drugoi, i est' naibolee veroyatnoe proyavlenie sushestvovaniya "chernyh dyr" (ob'ekt Lebed' H-1). Massa etogo ob'ekta poryadka 10-12 mass Solnca, t. e. mnogo bol'she massy stacionarnyh zvezd, sostoyashih iz vyrozhdennogo gaza.

<< § 3.2 Ravsnovesie i ustoichivost' zvezd | Oglavlenie | § 3.4 Harakternye vremena otdel'nyh etapov evolyucii zvezd >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

$\Pi_1 = pm_e\hbar^{-2}n_e^{-5/3} ;$	(3.36)
$\Pi_2 = p\hbar^{-1}c^{-1}n_e^{-4/3} .$	(3.37)