po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 3.5 Vyrazhenie massy i svetimosti zvezd cherez mirovye postoyannye | Oglavlenie | § 4.2 Politropnye i konvektivnye zvezdy >>

Glava IV. Princip podobiya v chislennom modelirovanii stacionarnyh zvezd

V nastoyashei glave my prodolzhim analiz svoistv zvezd uzhe na osnove principa podobiya. Eto pozvolit poluchit' bolee detal'nye harakteristiki, v chastnosti, opredelit' i chislennye znacheniya bezrazmernyh kompleksov.

Razumeetsya, nastoyashaya glava ne pretenduet na skol'ko-nibud' polnoe izlozhenie teorii vnutrennego stroeniya zvezd. Osnovnoe vnimanie udelyaetsya usloviyam podobiya zvezdnyh modelei.

Ves' analiz struktury i evolyucii zvezd osnovan na chislennom modelirovanii. Uravneniya vnutrennego stroeniya zvezd otnositel'no prosty i poetomu ih chislennoe reshenie bylo netrudno poluchit' eshe do nastupleniya "ery EVM". Sozdanie bystrodeistvuyushih EVM dalo vozmozhnost' postroit' bol'shoe chislo zvezdnyh modelei, analiz i sravnenie s nablyudeniyami kotoryh pozvolili daleko prodvinut'sya v ponimanii zvezdnoi evolyucii.

Sopostavlenie teorii s nablyudeniyami osnovano na sravnenii teoreticheskih zavisimostei mezhdu osnovnymi parametrami zvezd (massa M, svetimost' L, radius R) i podobnymi zhe statisticheskimi dannymi, poluchennymi na osnove nablyudenii bol'shogo chisla zvezd. V chastnosti, osoboe znachenie imeet statisticheskii analiz grupp zvezd, svyazannyh obshnost'yu proishozhdeniya, naprimer, vhodyashih v galakticheskie skopleniya. Pravda, takie sopostavleniya ne vsegda dostatochno kritichny, poskol'ku teoreticheskie zavisimosti mezhdu M, L i R v nekotoryh sluchayah slabo zavisyat ot vybora teoreticheskih modelei. Uzhe otmechalos', chto sootnoshenie massa - svetimost' pochti ne zavisit ot vybora zakona vydeleniya energii. No tem ne menee vazhno podcherknut', chto teoreticheskie i nablyudaemye zavisimosti mezhdu M, L i R, kak pravilo, horosho soglasuyutsya mezhdu soboi.

Est' dve bolee neposredstvennye nablyudatel'nye proverki teorii stroeniya zvezd: po dvizheniyu linii apsid v tesnyh dvoinyh sistemah i po neitrinnomu izlucheniyu Solnca. Metod opredeleniya stepeni neodnorodnosti modeli (koncentracii plotnosti k centru) po dvizheniyu linii apsid podrobno opisan, naprimer, v knige Shvarcshil'da [1]. Zdes' takzhe teoriya okazalas' v horoshem soglasii s nablyudeniyami, no i etot metod sravneniya nedostatochno kritichen. Krome togo, ego udalos' poka primenit' k ochen' nebol'shomu chislu zvezd tol'ko verhnei chasti glavnoi posledovatel'nosti. Bolee interesna proverka po neitrinnomu izlucheniyu, hotya ona, po krainei mere poka, mozhet byt' ispol'zovana tol'ko dlya analiza modelei Solnca. Izmeryaya potok neitrino ot Solnca, mozhno neposredstvenno sudit' ob usloviyah v ego central'nyh chastyah. Kak horosho izvestno, eksperimenty Devisa priveli k zametnomu rashozhdeniyu teorii i nablyudenii (poslednii obzor vsei etoi problemy izlozhen v rabotah [2, 3]). Poka (1975 g.) ne yasno, kak udastsya preodolet' etu trudnost', sohraniv nashi osnovnye predstavleniya o haraktere i roli razlichnyh termoyadernyh reakcii v zvezdah i ob ih stroenii i evolyucii. No my v dal'neishem budem schitat' eti predstavleniya pravil'nymi.

Analiz chislennyh modelei stroeniya zvezd dal ochen' mnogoe i bylo by ves'ma nerazumno otkazyvat'sya ot etogo bol'shogo ob'ema informacii tol'ko iz-za togo, chto my ne mozhem preodolet' nekotorye trudnosti.

Razvitie teorii chislennogo modelirovaniya zvezd proshlo neskol'ko etapov. Na pervyh porah shiroko ispol'zovalsya princip podobiya - predpolagalos', chto zvezdy s raznymi znacheniyami osnovnyh parametrov mogut imet' podobnoe stroenie, opisyvaemoe odnimi i temi zhe bezrazmernymi uravneniyami s odnimi i temi zhe znacheniyami bezrazmernyh kompleksov. Takoe predpolozhenie pozvolilo srazu zhe poluchit' teoreticheskie zavisimosti mezhdu M, L i R, t. e. imenno to, chto i podlezhit sravneniyu s nablyudeniyami v pervuyu ochered'.

Odnako primenenie principa podobiya nalagaet opredelennye ogranicheniya na sootnosheniya, opisyvayushie fizicheskie processy v nedrah zvezd. K sozhaleniyu, pri primenenii principa podobiya v teorii stroeniya i evolyucii zvezd mozhno ispol'zovat' tol'ko priblizhennye formuly, opisyvayushie neprozrachnost' i moshnost' vydeleniya energii. Poetomu po mere razvitiya teorii vse bol'she i bol'she poyavlyalos' rabot po raschetam konkretnyh modelei. Inymi slovami, dlya kazhdogo zadannogo znacheniya M, L i R i predpolozhennogo himicheskogo sostava rasschityvalas' svoya model'. Zavisimosti mezhdu etimi parametrami teper' uzhe opredelyayutsya na osnove analiza sovokupnosti etih modelei. Ispol'zovanie moshnyh EVM sdelalo raschet bol'shogo chisla konkretnyh modelei ne slishkom trudoemkoi rabotoi. Razumeetsya, takoi analiz bol'shogo chisla konkretnyh modelei daet bolee dostovernye dannye (v ramkah sdelannyh dopushenii), chem rezul'taty primeneniya principa podobiya, osnovannye na uproshennyh sootnosheniyah. Tem ne menee, a osobenno uchityvaya i nekotoruyu imeyushuyusya neuverennost' v ishodnyh predposylkah, predstavlyaet opredelennyi interes i analiz vyvodov, osnovannyh na metode podobiya. Oni bolee naglyadny, poluchayutsya bolee prostym putem i pozvolyayut yasnee ponyat', v chem mogut zaklyuchat'sya te ili inye trudnosti. Zdes' my dadim obzor rezul'tatov, poluchennyh v teorii vnutrennego stroeniya i evolyucii zvezd putem primeneniya principa podobiya.

§ 4.1 Osnovnye uravneniya teorii vnutrennego stroeniya zvezd

Osnovnye uravneniya, opisyvayushie vnutrennee stroenie zvezd, privodilis' mnogokratno v special'nyh monografiyah [1, 4, 5] i uchebnikah [6, 7]. Kachestvennoe izlozhenie fizicheskogo smysla uravnenii izlagalos' i v nauchno-populyarnoi literature (sm. [8]). Nado takzhe otmetit', chto byl opublikovan ryad sbornikov [9-11], gde eti uravneniya takzhe podrobno opisyvalis'. Zdes' my ogranichimsya lish' kratkim poyasneniem.

Vo-pervyh, predpolozhim sfericheskuyu simmetrichnost' zvezdy. Dlya bol'shinstva zvezd eto uslovie vypolneno s ogromnoi tochnost'yu. Dazhe bystro vrashayushiesya zvezdy pochti sfericheski-simmetrichny. Bolee zametny otkloneniya ot sfericheskoi simmetrii u zvezd, vhodyashih v tesnye dvoinye sistemy. No eto osobyi sluchai, poskol'ku nel'zya rassmatrivat' stroenie odnoi zvezdy, ne obrashaya vnimaniya na ee komponentu.

Vo-vtoryh, my budem prenebregat' vliyaniem magnitnogo polya na strukturu zvezdy. Eto otdel'naya i, k sozhaleniyu, ves'ma neopredelennaya problema, poskol'ku nikakih dannyh o magnitnyh polyah v nedrah zvezd u nas net. Nekotorye kachestvennye soobrazheniya na osnove teorii razmernostei budut privedeny v sleduyushei glave.

V-tret'ih, my budem schitat' zvezdy stacionarnymi ili, po krainei mere, kvazistacionarnymi ob'ektami. V deistvitel'nosti lyubaya zvezda evolyucioniruet, no esli svyazannye s etim izmeneniya proishodyat medlenno, to v uravneniyah zvezdnoi struktury mozhno opustit' chleny, yavno opisyvayushie izmenenie parametrov so vremenem.

Teper' zapishem sami uravneniya. V stacionarnoi zvezde imeet mesto gidrostaticheskoe ravnovesie, opisyvaemoe sootnosheniem

$\frac{dp}{dr} = -\frac{GM(r)}{r^2}\rho.$ (4.1)

Zdes' r - polnoe davlenie veshestva i izlucheniya, ρ - plotnost' veshestva, M(r) - massa, zaklyuchennaya vnutri sfery s radiusom r (rasstoyaniem ot centra), G - postoyannaya tyagoteniya. Velichina M(r) mozhet byt' opredelena integral'nym ili differencial'nym sootnosheniem

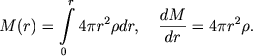
$M(r) = \int\limits_0^r 4\pi r^2 \rho dr, \quad \frac{dM}{dr} = 4\pi r^2 \rho.$ (4.2)

Vnutri zvezd otklonenie ot termodinamicheskogo ravnovesiya ochen' malo i poetomu davlenie veshestva i izlucheniya opredelyaetsya plotnost'yu ρ, temperaturoi gaza i ravnovesnogo (chernotel'nogo) izlucheniya T. Dlya zvezd, postroennyh iz obychnogo gaza, t. e. takih, gde net vyrozhdeniya elektronnogo gaza, polnoe davlenie skladyvaetsya iz davleniya ideal'nogo gaza i davleniya izlucheniya:

$p = \frac{\mathfrak{R}}{\mu}\rho T + \frac{1}{3}aT^4,$ (4.3)

gde ℜ - universal'naya gazovaya postoyannaya, μ - molekulyarnyi ves (atomnyi ves, prihodyashiisya na odnu chasticu), a - postoyannaya plotnosti izlucheniya ( $a = 4\sigma /c = \pi^2k^4/15\, (\hbar c)^3$ ). V nedrah zvezd vodorod, gelii i drugie ne slishkom tyazhelye elementy ionizovany pochti polnost'yu i poetomu dlya molekulyarnogo vesa imeem

$\mu = \frac{1}{2X + \frac{3}{4}Y + \frac{1}{2}Z} \approx \frac{4}{3+5X},$ (4.4)

gde X - dolya vodoroda, U - dolya geliya, Z - dolya vseh ostal'nyh elementov (po vesu). Tak kak X + U + Z = 1 i obychno Z << l, to mozhno pol'zovat'sya vtoroi formuloi (4.4).

V belyh karlikah, a takzhe v central'nyh chastyah drugih zvezd elektronnyi gaz mozhet byt' vyrozhdennym. Vyrazhenie dlya davleniya nerelyativistskogo elektronnogo vyrozhdennogo gaza v sluchae, kogda ego temperatura blizka k nulyu, bylo dano formuloi (3.44). Teper' privedem sootvetstvuyushuyu formulu s uchetom temperaturnoi popravki:

$p = \frac{(3\pi^2)^{2/3}\hbar^2}{5m_e m_p^{5/3}}\left(\frac{\rho}{\mu_e}\right)^{5/3} + \frac{(3\pi^2)^{1/3}m_e}{9\hbar^2 m_p^{1/3}}\left(\frac{\rho}{\mu_e}\right)^{1/3} (kT)^2.$ (4.5)

Pri sil'nom vyrozhdenii elektronnogo gaza eta formula okazyvaetsya spravedlivoi i pri dostatochno vysokoi temperature. Analogichnaya formula dlya relyativistskogo vyrozhdennogo gaza imeet vid

$p = \frac{(3\pi^2)^{2/3}\hbar c}{4 m_p^{4/3}}\left(\frac{\rho}{\mu_e}\right)^{4/3} + \frac{(3\pi^2)^{2/3}}{18\hbar c m_p^{2/3}}\left(\frac{\rho}{\mu_e}\right)^{2/3} (kT)^2.$ (4.6)

Zdes' μ_e - molekulyarnyi ves, prihodyashiisya na odin elektron. Imeem

$\mu_e = \frac{1}{X + \frac{1}{2}(Y+Z)} \approx \frac{2}{1+X}.$ (4.7)

Nado takzhe uchityvat' i davlenie gaza, sostoyashego iz atomnyh yader. Ego mozhno opisat' obychnym uravneniem Klapeirona. Pervye chleny sootnoshenii (4.5) i (4.6), kak my uzhe znaem, yavlyayutsya chastnym sluchaem uzhe horosho izvestnoi politropnoi zavisimosti mezhdu davleniem i plotnost'yu:

$p(\rho) = K_{\gamma}\rho^{\gamma} = K_\gamma\rho^{1+\frac{1}{n}}.$

Politropnoe uravnenie sostoyaniya okazyvaetsya ochen' poleznym v primenenii metoda podobiya. No, kak sleduet iz privedennyh vyshe formul, v real'nyh usloviyah zvezdnogo veshestva strogoe politropnoe sootnoshenie vstrechaetsya redko. Odnako okazyvaetsya, chto po krainei mere v nekotoryh zadachah mozhno sohranit' princip podobiya, ispol'zovav sootnoshenie

$p(\rho) = K_{\gamma}\rho^{\gamma} + K_\alpha\rho^\alpha,$ (4.8)

gde &K_α i α tozhe nekotorye postoyannye. Naprimer, v osnovnoi oblasti vyrozhdennogo gaza v belyh karlikah ili v izotermicheskih vyrozhdennyh yadrah zvezd-gigantov temperatura pochti odinakova po vsei oblasti. Zdes' vpolne mozhno ispol'zovat' (4.8) pri α = 1/3 v sluchae (4.5) i α = 2/3 v sluchae (4.6).

Perehod ot nerelyativistskogo k relyativistskomu vyrozhdennomu elektronnomu gazu mozhno opisat' izmeneniem pokazatelya politropy. Naprimer, postepennaya relyativizaciya elektronov po mere uvelicheniya plotnosti mozhet byt' uchtena zamenoi pokazatelya 5/3 v (4.5) na velichinu

$\gamma = \frac{5}{3} \left[1 - \frac{1}{7}\left(\frac{\hbar}{m_e c}\right)^2 \left(\frac{3\pi^2\rho}{\mu_e m_p }\right)^{2/3} + ...\right].$ (4.9)

Analogichnym obrazom mozhet byt' uchtena i nepolnaya relyativizaciya elektronov v (4.6) putem zameny 4/3 pa pokazatel'

$\gamma = \frac{4}{3} \left[1 + \frac{3}{4}\left(\frac{m_e c}{\hbar}\right)^2 \left(\frac{\mu_e m_p }{3\pi^2\rho}\right)^{2/3} + ...\right].$ (4.10)

Razumeetsya, formuly (4.9) i (4.10) spravedlivy, poka vtorye chleny v skobkah zametno men'she edinicy.

Konkretno, ispol'zovanie sootnoshenii (4.9) i (4.10) mozhet svodit'sya k sleduyushemu. Rasschityvayutsya podobnye modeli s fiksirovannym, no neopredelennym zaranee γ , a zatem podbiraetsya velichina etogo pokazatelya tak, chtoby ego znachenie sootvetstvovalo by harakternoi ploskosti vyrozhdennogo yadra zvezdy.

Temperatura gaza i izlucheniya, vhodyashaya v uravnenie (4.3), opredelyaetsya usloviyami perenosa energii. Kak pravilo, istochniki energii deistvuyut v central'nyh chastyah zvezdy, i perenos ee naruzhu okazyvaetsya sushestvennym dlya opredeleniya vsei struktury zvezdy. Izvestno neskol'ko mehanizmov perenosa energii: konvektivnyi, luchistyi, elektronnoi teploprovodnost'yu. Naibolee effektiven mehanizm konvektivnogo perenosa energii, no on ne vsegda vozmozhen.

Privedem nekotorye osnovnye dannye ob adiabaticheskom konvektivnom perenose energii, kotorye ponadobyatsya v etoi glave. V glubokih sloyah zvezdy konvekciya imeet adiabaticheskii harakter. Element massy gaza, sluchaino okazavshiisya bolee nagretym, podnimaetsya vverh i rasshiryaetsya po adiabaticheskomu zakonu. Drugie elementy, bolee holodnye, opuskayutsya vniz, szhimayas' takzhe po adiabaticheskomu zakonu. Vysota pod'ema ili opuskaniya konvektivnyh elementov, nazyvaemaya dlinoi peremeshivaniya, obychno poryadka ekvivalentnoi vysoty raspredeleniya plotnosti ili davleniya.

Poskol'ku dvizhenie gaza opredelyaetsya adiabaticheskoi zavisimost'yu, to v oblasti konvektivnogo perenosa raspredelenie plotnosti i davleniya takzhe dolzhno opredelyat'sya adiabaticheskimi izmeneniyami, a imenno zdes' imeet mesto politropnoe sootnoshenie, gde teper' pokazatel' γ est' otnoshenie teploemkosti pri postoyannom davlenii k teploemkosti pri postoyannom ob'eme.

Znachenie pokazatelya γ zavisit ot stepeni ionizacii gaza i ot roli luchevogo davleniya. Tam, gde ionizaciya pochti polnaya (glubokie sloi zvezdy) i gde gaz mozhno schitat' odioatomnym, pokazatel' γ raven (sm. [5])

$\gamma_1 = \left(\frac{\partial \ln p}{\partial \ln \rho}\right)_{\mbox{ad}} = \frac{32 - 24\beta - 3\beta^2}{3(8 - 7\beta)} \approx \frac{5}{3}\beta,$ (4.11)

gde β - otnoshenie gazovogo davleniya k polnomu, t. e.

$\beta = \frac{p_g}{p} = \frac{1}{1 + \frac{a\mu m_p}{3k}\frac{T^3}{\rho}}.$ (4.12)

Uslovie $\gamma_1 \approx \frac{5}{3}\beta$ spravedlivo pri 1 - β ≪ 1. Takim obrazom, v oblasti perenosa energii konvekciei davlenie i plotnost' svyazany politropnoi zavisimost'yu, gde pokazatel', odnako, tozhe mozhet menyat'sya pri izmenenii β s glubinoi. Uslovie politropnoi zavisimosti opredelyaet i gradient temperatury v etoi oblasti. Luchshe zapisat' srazu vyrazhenie dlya logarifmicheskogo adiabaticheskogo gradienta temperatury po davleniyu:

$\nabla_{\mbox{ad}} = \left(\frac{\partial \ln T}{\partial \ln \rho}\right)_{\mbox{ad}} = \frac{p}{T}\frac{\partial T}{\partial p} = \frac{\gamma_2 - 1}{\gamma_2} = \frac{2(4-3\beta)}{32 - 24\beta - 3\beta^2} = \frac{2}{5}(3\beta - 2) + ...,$ (4.13)

gde pokazatel' γ₂ otlichaetsya ot γ₁ v sluchae bol'shoi roli izlucheniya:

$\gamma_2 = \frac{32 - 24\beta - 3\beta^2}{24 - 18\beta - 3\beta^2} = \frac{5}{3}(2\beta - 1) + ...$

Ochevidno, chto γ₁ = γ₂ = 5/3 v sluchae β = 1. Razlichie mezhdu γ₁ i γ₂ svyazano s tem, chto pri β ≠ 1 veshestvo zvezdy predstavlyaet soboi gaz s dvumya politropami, kak, naprimer, v formule (4.8) s raznymi pokazatelyami (γ = 5/3, α = 4/3). Formuly (4.14) i (4.13) opredelyayut "effektivnye politropnye pokazateli" polnogo izmeneniya sostoyaniya pri adiabaticheskih izmeneniyah.

S glubinoi velichina β menyaetsya (esli isklyuchit' sluchai ρ ∼ T³), kak eto sleduet iz (4.13). No eto izmenenie otnositel'no neveliko i, krome togo, v real'nyh zvezdah vsegda β sravnitel'no blizko k edinice. Takim obrazom, konvektivnyi perenos energii tozhe opisyvaetsya politropoi s medlenno menyayushimsya pokazatelem. Bolee togo, effektivnaya velichina γ menyaetsya i blagodarya izmeneniyu sostoyaniya ionizacii veshestva. Pravda, v glubokih sloyah zvezd, gde vodorod, gelii i drugie legkie elementy ionizovany pochti polnost'yu, etim effektom mozhno prenebrech', no on ves'ma sushestven pri analize konvekcii v sloyah zvezd vblizi poverhnosti. No zdes' vazhno uchityvat' i otkloneniya ot adiabatichnosti. V sleduyushei glave budet neskol'ko podrobnee obsuzhdat'sya sluchai konvekcii vo vneshnih sloyah zvezd.

Po formule (4.13) mozhno opredelyat' gradient temperatury tol'ko v tom sluchae, kogda molekulyarnyi ves ne menyaetsya. Esli uchest' i etot effekt, to k ∇_ad v (4.13) dobavlyaetsya eshe odno slagaemoe:

$\nabla_\mu = \frac{\beta}{4-3\beta}\frac{d \ln\mu}{d \ln p}.$

Formula (4.13) vmeste s formuloi (4.1) opredelyaet i gradient temperatury po glubine, t. e. velichinu dT/dr v oblasti perenosa energii adiabaticheskimi konvektivnymi dvizheniyami.

Perenos energii elektronnoi teploprovodnost'yu okazyvaetsya sushestvennym lish' v oblastyah, gde veliko vyrozhdenie elektronnogo gaza. K etomu voprosu my vernemsya, kogda budem rassmatrivat' podobnye ob'ekty.

Pereidem, nakonec, k luchistomu perenosu energii, kotoryi igraet ochen' vazhnuyu rol' v opredelenii struktury podavlyayushego bol'shinstva zvezd, i k analizu istochnikov energii. Kak pravilo, uravnenie luchistogo perenosa zapisyvaetsya v diffuzionnom priblizhenii:

$D_r = \frac{d}{dr}(aT^4) = -\frac{L(r)}{4\pi r^2}.$ (4.14)

Zdes' D_r - koefficient diffuzii energii izlucheniya, velichina L(r) est' kolichestvo energii, generiruemoi vnutri sfery radiusa r. Po opredeleniyu,

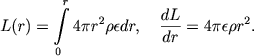
$L(r) = \int\limits_0^r 4\pi r^2 \rho\epsilon dr, \quad \frac{dL}{dr} = 4\pi \epsilon\rho r^2.$ (4.15)

Zdes' ε - kolichestvo energii, osvobozhdayusheisya v edinice massy za edinicu vremeni. Koefficient diffuzii luchistoi energii mozhno vyrazit' cherez dlinu svobodnogo probega kvantov l: D_r = 1/3 lc. Vmesto l udobno vvesti koefficient neprozrachnosti ϰ no formule l = 1/ϰr i perepisat' sootnoshenie (4.14) v takom vide:

$\frac{d}{dr}\left[\frac{1}{3} aT^4\right] = -\frac{\varkappa L(r)}{4\pi r^2c}\rho.$ (4.16)

Eta forma zapisi udobna i tem, chto 1/3 aT⁴ est' luchevoe davlenie, a formuly (4.16) i (4.1) imeyut analogichnyi vid.

Velichiny ϰ i ε , tochnee, ih zavisimosti ot parametrov sredy r i T i ot himicheskogo sostava, igrayut bol'shuyu rol' v teorii vnutrennego stroeniya zvezd. Ochen' mnogo vnimaniya udelyalos' vychisleniyu etih parametrov. Obsuzhdenie etih vychislenii i ih rezul'taty podrobno privodilis' v citirovannyh vyshe monografiyah po vnutrennemu stroeniyu zvezd i, v chastnosti, v stat'yah Rivsa i Koksa (sm. sbornik [9]). Koefficient neprozrachnosti teper' obychno zadaetsya v tablichnoi forme. Dlya sovremennyh raschetov na EVM prostye analiticheskie sootnosheniya uzhe okazyvayutsya nedostatochnymi. Velichiny ε - moshnosti istochnikov - eshe mogut byt' zapisany v analiticheskom vide. No i zdes' nekotorye popravochnye mnozhiteli zadayutsya v tablichnoi forme.

Dlya nashei zadachi - primenenie metoda podobiya k teorii stroeniya zvezd - neobhodimy analiticheskie formuly dlya velichin ϰ i ε . Bolee togo, eti formuly dolzhny byt' prostogo stepennogo vida.

Pervoe priblizhenie v teorii perenosa energii izlucheniem privodit k izvestnoi formule Kramersa, uzhe obsuzhdavsheisya v gl. 2:

$\varkappa = \varkappa_0\frac{\rho}{T^{7/2}},$ (4.17)

gde velichina ϰ₀ zavisit ot himicheskogo sostava i sostoyaniya ionizacii. Esli koncentraciya tyazhelyh elementov Z ne slishkom mala, to osnovnoi vklad v neprozrachnost' daet vzaimodeistvie elektronov s etimi elementami:

$\varkappa_0 \approx 10^{25}Z(1+X)\frac{\mbox{grad}^{7/2}}{\mbox{g}^2} \cdot \mbox{sm}^5.$ (4.18)

Zdes' mnozhitel' 1 + X opredelyaet otnositel'noe chislo svobodnyh elektronov. S drugoi storony, v veshestve, sostoyashem pochti isklyuchitel'no iz ionizovannyh vodoroda i geliya, osnovnym istochnikom poglosheniya yavlyaetsya tormozhenie elektronov v elektricheskom pole etih yader i

$\varkappa_0 \approx 3 \cdot 10^{22}(1+X)\frac{\mbox{grad}^{7/2}}{\mbox{g}^2} \cdot \mbox{sm}^5.$ (4.19)

Zdes' uchteno, chto H + U ≈ 1. Formula (4.19) ispol'zuetsya tol'ko pri Z ≲ 3 ⋅ 10^-3.

Kachestvennoe ob'yasnenie obshei zavisimosti (4.17) legko poluchit' iz sleduyushih soobrazhenii [4]. Ochevidno, chto dlina svobodnogo probega kvanta dolzhna byt', s odnoi storony, proporcional'na plotnosti izlucheniya, t. e. aT⁴, a s drugoi storony, dolzhna byt' obratno proporcional'na veroyatnosti poglosheniya kvanta. Poslednyaya tem bol'she, chem bol'she koncentraciya elektronov i ionov i teplovaya skorost' elektronov v_Te ∼ T^½. Otsyuda imeem

$l = \frac{1}{\varkappa\rho} \sim \frac{aT^4}{n_e n_p v_{Te}} \sim \frac{T^{7/2}}{\rho^2(1+X)}.$

Podstaviv eto vyrazhenie v opredelenie $\varkappa \sim 1/(\rho l)$ poluchaem formulu Kramersa.

Na samom dele koefficient poglosheniya zavisit ot himicheskogo sostava, plotnosti i temperatury bolee slozhnym obrazom, chem eto sleduet iz prostoi formuly Kramersa. Poetomu dlya bol'shei obshnosti pol'zuyutsya takim sootnosheniem

$\varkappa(X, Y, Z, \rho, T) \approx \varkappa_0\frac{\rho^\alpha}{T^\nu},$ (4.20)

gde ϰ₀(H, Y, Z), α i ν - nekotorye znacheniya parametrov, podbiraemye iz usloviya luchshego soglasiya tablichnyh dannyh s formuloi (4.20).

Obychno v osnovnoi chasti nedr zvezd parametry ν i α menyayutsya ne ochen' sil'no. S uvelicheniem temperatury os neskol'ko umen'shaetsya (primerno do α ≈ 0,9-0,8). Pokazatel' ν chasto blizok k 7/2, no umen'shaetsya s rostom plotnosti (do ν ≈ 2). Vse tri parametra zavisyat i ot himicheskogo sostava.

V ochen' goryachei plazme, gde imeet mesto polnaya ionizaciya, osnovnym mehanizmom neprozrachnosti yavlyaetsya rasseyanie sveta na svobodnyh elektronah. Zdes' neprozrachnost' opredelyaetsya ochen' prostoi formuloi, takzhe privedennoi ranee v gl. 2:

$\varkappa = \frac{8\pi}{3}\left(\frac{e^2}{m_e c^2}\right)\frac{\mu_e}{m_p} \approx 0,2(1+X) \frac{\mbox{sm}^2}{\mbox{g}}.$ (4.21)

Ochevidno, chto (4.21) mozhno schitat' chastnym sluchaem (4.20) pri α = ν = 0.

Formula Kramersa neprimenima i v sluchae ochen' nizkih temperatur, kogda stepen' ionizacii mala. V oblasti temperatur poryadka neskol'kih tysyach gradusov imeem sleduyushie zavisimosti (sm. stat'yu Steina v sbornike [10]). Dlya zvezd naseleniya pervogo tipa, dostatochno bogatyh geliem i tyazhelymi elementami (H=0,6, Y=0,38, Z=0,02), koefficient neprozrachnosti

$\varkappa \approx 2 \cdot 10^{-20}\rho^{0,7}T^{6,3} \frac{\mbox{sm}^2}{\mbox{g}}.$ (4.22)

S drugoi storony, u zvezd naseleniya vtorogo tipa, gde geliya i, osobenno, tyazhelyh elementov ochen' malo (H = 0,9, Y = 0,099, Z = 0,001), koefficient neprozrachnosti

$\varkappa \approx 3 \cdot 10^{-35}\rho^{0,6}T^{10,4} \frac{\mbox{sm}^2}{\mbox{g}}.$ (4.23)

Eti formuly takzhe mozhno rassmatrivat' kak chastnye sluchai zavisimosti (4.20), gde α ≈ 0,6-0,7, a parametr v okazalsya ochen' bol'shim po absolyutnoi velichine i, chto samoe glavnoe, otricatel'nym. Eshe raz napomnim, chto sootnosheniya (4.22) i (4.23) primenimy tol'ko pri nizkih temperaturah. Obshii hod koefficientov neprozrachnosti dan na ris. 1. Grubuyu ocenku maksimuma ϰ mozhno poluchit' iz peresecheniya krivyh (4.22) ili (4.23) s (4.17), a minimal'noe znachenie ϰ pri dostatochno vysokih temperaturah opredelyaetsya (4.21).

Pereidem teper' k opredeleniyu funkcii ε - moshnosti istochnikov energii. Podrobnoe izlozhenie teorii i svodki vseh ispol'zuemyh zdes' formul dany, naprimer, v stat'yah Rivsa v [9] i [10]. Zdes', kak i v sluchae koefficienta neprozrachnosti, my ogranichimsya zapis'yu osnovnyh priblizhennyh sootnoshenii.

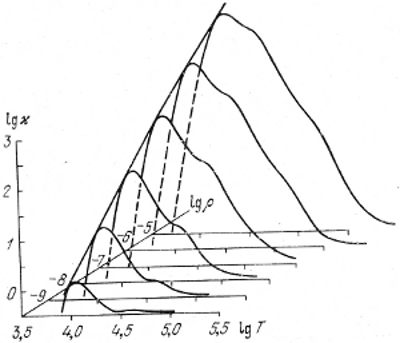
Ris. 1. Grafik zavisimosti koefficienta neprozrachnosti ot temperatury i plotnosti gaza.
Krutoi sklon sleva - oblast' nepolnoi ionizacii (formula (4.22)). Pravaya spadayushaya chast' krivyh - oblast' formuly Kramersa, asimptoty - oblast' tomsonovskogo rasseyaniya (4.21).

No prezhde o haraktere etih sootnoshenii. Veroyatnost' termoyadernyh reakcii opredelyaetsya v pervuyu ochered' proniknoveniem reagiruyushih yader cherez potencial'nyi bar'er. Sootvetstvuyushii chlen v vyrazhenii dlya e imeet slozhnuyu eksponencial'nuyu zavisimost' ot temperatury. Predeksponencial'nyi mnozhitel' takzhe zavisit ot temperatury, krome togo, zavisit ot plotnosti, ot nalichiya opredelennyh i ne vsegda izvestnyh rezonansov vzaimodeistviya yader i ot himicheskogo sostava. Eti zavisimosti ne vsegda udaetsya predstavit' v analiticheskom vide. Uslozhnyaet zadachu i neobhodimost' ucheta nekotoryh popravok. Tem ne menee i tut mozhno zapisat' dlya velichiny e priblizhennye formuly v vide stepennyh zavisimostei:

$\epsilon(X, Y, Z, \rho, T) = \epsilon_0\rho^mT^n.$ (4.24)

Zdes' ε₀ zavisit tol'ko ot himicheskogo sostava, m i n - nekotorye chisla, kotorye mogut slabo izmenyat'sya s temperaturoi. Zavisimost' ε₀ ot himicheskogo sostava opredelyaetsya ne tol'ko polnoi koncentraciei tyazhelyh elementov, no i otnositel'nym soderzhaniem razlichnyh yader, kak, naprimer, gelii-3, azot, uglerod i t. p. Poetomu my ne budem vypisyvat' yavnyh zavisimostei ε₀ ot himicheskogo sostava. Bolee togo, ne budem privodit' i chislennyh znachenii ε₀, otsylaya chitatelya za podrobnostyami k citirovannym stat'yam Rivsa. Zametim tol'ko, chto v opredelenii velichiny ε₀ eshe mnogo neodnoznachnostei.

Parametr m opredelyaetsya prosto. Esli osnovnaya reakciya v cepi predstavlyaet soboi stolknovenie dvuh yader, to m = 1. V sluchae reakcii, proishodyashei pri odnovremennom stolknovenii treh yader, m = 2. Parametr n opredelyaetsya prohozhdeniem yader cherez potencial'nyi bar'er. Dlya reakcii so stolknoveniem dvuh yader imeem dlya pokazatelya n sleduyushuyu zavisimost':

$\epsilon(X, Y, Z, \rho, T) = \epsilon_0\rho^mT^n.$ (4.25)

gde Z₁e i Z₂e - zaryady reagiruyushih yader, m₁₂ = m₁m₂/(m₁+m₂) - ih privedennaya massa. Vidno, chto pokazatel' n zavisit ot temperatury, no eta zavisimost' otnositel'no slabaya i v opredelennom intervale temperatur velichinu n mozhno schitat' postoyannoi.

Pri postroenii modelei na osnove principa podobiya parametry ε₀, m i n schitayutsya postoyannymi po vsei zvezde. Hotya v deistvitel'nosti eto i ne tak, no na samom dele voznikayushaya zdes' oshibka nevelika, poskol'ku vydelenie energii sosredotocheno v ochen' malyh oblastyah, gde izmeneniya etih parametrov sovsem ne sushestvenny (sm. nizhe).

Izvestno neskol'ko termoyadernyh reakcii, imeyushih sushestvennoe znachenie dlya energetiki zvezd. Nizhe my ih perechislim i privedem sootvetstvuyushie znacheniya parametrov m i n.

1. Proton-protonnyi cikl. Iz chetyreh protonov obrazuetsya yadro Ne⁴. V promezhutochnyh stadiyah poyavlyayutsya yadra N², Ne³, Li⁷, Be⁷ i Be⁸, a takzhe V⁸. Reakciya s berilliem i borom otvetstvenna za izluchenie neitrino Solncem. Osnovnaya reakciya cikla - obrazovanie deiteriya iz dvuh protonov. Zdes' m = 1 i

$n = \frac{11,3}{\sqrt[3]{T_6}} - \frac{2}{3}.$ (4.26)

Vyrazhenie T₆ oznachaet, chto temperatura zapisana v millionah gradusov. Reakciya proton-protonnogo cikla dominiruet pri otnositel'no nizkih temperaturah (T₆ ≈ 10-18). Zdes' n ≈ 4.

2. Uglerodno-azotno-kislorodnyi cikl. Iz chetyreh protonov takzhe obrazuetsya yadro geliya, po teper' v promezhutochnyh reakciyah prinimayut uchastie yadra S¹², S¹³, N¹³, N¹⁴, N¹⁵, O¹⁵, O¹⁶, O¹⁷, F¹⁷. Skorost' vydeleniya energii limitiruetsya reakciei soedineniya azota N¹⁴ i protona. Zdes', po-prezhnemu, m = 1, a

$n = \frac{50,8}{\sqrt[3]{T_6}} - \frac{2}{3}.$ (4.27)

Etot cikl sushestven pri bolee vysokih temperaturah (T₆ ≳ 18) i pokazatel' n ≈ 16.

Etimi dvumya ciklami ischerpyvaetsya prevrashenie vodoroda v gelii. Zatem, pri bolee vysokih temperaturah, nachinaetsya prevrashenie geliya v bolee tyazhelye elementy.

3. Esli primes' tyazhelyh elementov k obogashennomu geliem veshestvu mala, to proishodit process soedineniya treh yader geliya v odno yadro ugleroda S¹² pri troinom stolknovenii. Poetomu m = 2. Pokazatel' p opredelyaetsya proniknoveniem cherez bar'er slozhnoi sistemy treh yader. V rezul'tate poluchaem

$n = \frac{43,5}{\sqrt[3]{T_8}} - 3.$ (4.28)

gde T₈ - temperatura, vyrazhennaya v sotnyah millionov gradusov. Eta reakciya, kak i drugie gelievye reakcii, protekayut pri temperaturah, bol'shih 0,7 ⋅ 10⁸ gradusov.

4. Esli veliko soderzhanie ugleroda, to vozmozhno pogloshenie geliya ego yadrami s obrazovaniem kisloroda. Analogichno, yadra azota mogut takzhe pogloshat' yadra geliya s obrazovaniem ftora; yadra kisloroda, pogloshaya yadra geliya, obrazuyut yadra neona i t. d. Vo vseh podobnyh reakciyah m = 1 i parametr n pri T₈ ∼ 0,3-2

$n \approx \frac{23 \div 28}{\sqrt[3]{T_8}}.$ (4.29)

S rostom nomera yadra rastet i pokazatel' n . Dlya ochen' bol'shih temperatur T₈ ≥ 5 - 20 bol'shoi vklad vnosyat vysokie urovni vozbuzhdeniya yader i pokazatel' p obratno proporcionalen temperature, t. e. bystree umen'shaetsya s ee rostom.

5. Nakonec, pri ochen' vysokih temperaturah vstupayut v reakciyu mezhdu soboi i bolee tyazhelye elementy. Iz dvuh yader ugleroda obrazuetsya yadro magniya, iz dvuh yader kisloroda obrazuetsya yadro sery. Zdes', po-prezhnemu, m = 1, a pokazatel' p ochen' velik. Ves'ma priblizitel'no

$n \approx \frac{30 \div 45}{\sqrt[3]{T_9}}.$ (4.30)

Eshe raz otmetim, chto v stat'yah Rivsa (v sbornikah [9, 10]) dany bolee tochnye znacheniya etih parametrov.

Sil'naya zavisimost' moshnosti termoyadernyh istochnikov ot temperatury oznachaet, chto v real'nyh zvezdah vydelenie energii proishodit v otnositel'no nebol'shom ob'eme v centre zvezdy, libo v tonkom sloe, esli istochniki energii v centre zvezdy uzhe vygoreli. I v tom i v drugom sluchae v etih oblastyah temperatura menyaetsya neznachitel'no i poetomu mozhno schitat' parametr n postoyannym. Inymi slovami, rasschityvaya strukturu otdel'noi zvezdy, mozhno ishodit' iz formuly (4.24) s postoyannymi znacheniyami m in, no, perehodya ot odnoi zvezdy k drugoi, mozhno menyat' znachenie pokazatelya n v sootvetstvii s harakternoi temperaturoi toi oblasti, gde proishodit generaciya energii v etih zvezdah.

Imenno poetomu my priveli zdes' stol' podrobnye dannye o pokazatelyah n. Teper' u nas est' osnovnye uravneniya i ih parametry, opisyvayushie strukturu zvezdy. Pravda, eti uravneniya nado eshe napisat' v bolee udobnom vide i sformulirovat' granichnye usloviya. Eto budet sdelano v sleduyushih paragrafah pri rassmotrenii konkretnyh primerov.

<< § 3.5 Vyrazhenie massy i svetimosti zvezd cherez mirovye postoyannye | Oglavlenie | § 4.2 Politropnye i konvektivnye zvezdy >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce