Astronet > Razmernosti i podobie astrofizicheskih velichin

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 4.1 Osnovnye uravneniya teorii vnutrennego stroeniya zvezd | Oglavlenie | § 4.3 Belye karliki i neitronnye zvezdy >>

§ 4.2 Politropnye i konvektivnye zvezdy

Rassmotrim snachala bolee prostoi sluchai, kogda davlenie veshestva i ego plotnost' povsyudu vnutri zvezdy svyazany prostoi odnoznachnoi politropnoi zavisimost'yu. Kak uzhe otmechalos', priblizhenno takimi svoistvami obladayut libo te zvezdy, v kotoryh energiya celikom perenositsya konvekciei, libo zvezdy, davlenie v kotoryh svyazano v osnovnom s vyrozhdeniem elektronnogo ili neitronnogo gaza.

Pravda, v real'nyh zvezdah politropnaya zavisimost' s odnimi i temi zhe znacheniyami K_γ i γ ne mozhet opisyvat' vsei struktury. Naruzhnye sloi belyh karlikov sostoyat iz nevyrozhdennogo gaza, v ih central'nyh chastyah elektrony chastichno stanovyatsya relyativistskimi. Pokazatel' γ u konvektivnyh zvezd menyaetsya s glubinoi, da i malo veroyatno sushestvovanie zvezd, u kotoryh po vsei tolshe energiya perenositsya konvekciei - po krainei mere v ee atmosfernyh sloyah poyavlyaetsya i luchistyi perenos. Tem ne menee rassmotrenie politropnyh modelei s postoyannymi K_γ i γ okazyvaetsya ochen' poleznym. Ih mozhno schitat' pervym priblizheniem k zvezdnym modelyam i izuchat' na osnove politropnyh modelei nekotorye svoistva zvezd. Nakonec, zdes' naglyadnee vsego illyustriruetsya princip podobiya zvezdnyh modelei. V etom paragrafe budut rassmotreny obshie politropnye modeli. Zatem my obsudim ochen' prostoi sluchai polnost'yu konvektivnyh zvezd. Belye karliki i zvezdy budut rassmotreny v sleduyushem paragrafe.

Zapishem snova osnovnye uravneniya politropnoi modeli:

$\frac{dp}{dr} = -\frac{GM(r)}{r^2}\rho, \quad \frac{dM}{dr} = 4\pi\rho r^2, \quad p=K_\gamma\rho^\gamma.$ (4.31)

Etih uravnenii dostatochno dlya resheniya zadachi.

Sformuliruem teper' granichnye usloviya. V centre zvezdy pri r → 0 pervogo uravneniya imeetsya osobaya tochka; ochevidno, chto zdes' dolzhno byt' M(r) → 0. Krome togo, iz fizicheskih soobrazhenii mozhno potrebovat' ogranichennosti plotnosti i davleniya v centre zvezdy. Naruzhnuyu granicu zvezdy opredelim usloviem ρ = 0. Ochevidno, chto v etom sluchae soglasno (4.31) i davlenie dolzhno stremit'sya k nulyu.

Prezhde chem zanimat'sya resheniem uravnenii (4.31), vospol'zuemsya soobrazheniyami analiza razmernostei, uchityvaya osnovnye parametry zvezdy. Ochevidno, chto takovymi yavlyayutsya tol'ko polnaya massa M i radius R ob'ekta. Opredelyayushim parametrom takzhe yavlyaetsya i "politropnaya temperatura" K_γ. Iz chetyreh opredelyayushih parametrov: M, R, G i K_γ sostavlyaetsya odna bezrazmernaya kombinaciya, kotoruyu my uzhe opredelili v gl. 3 formuloi (3.17):

$\Pi_\gamma = K_\gamma C^{-1}M^{\gamma - 2}R^{4-3\gamma}.$ (4.32)

Chislennoe znachenie Π_γ iz soobrazhenii analiza razmernostei ne opredelyaetsya, poetomu v gl. 3 eta velichina ostalas' proizvol'noi. Teper' my ee naidem iz uravnenii (4.31). Privedem ih k bezrazmernomu vidu vvedeniem novyh bezrazmernyh peremennyh:

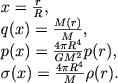
$\begin{array}{l} x=\frac{r}{R},\\ q(x) = \frac{M(r)}{M}, \\ p(x) = \frac{4\pi R^4}{GM^2}p(r), \\ \sigma(x) = \frac{4\pi R^4}{M}\rho(r). \end{array}$ (4.33)

Togda poluchim

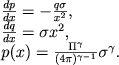
$\begin{array}{l} \frac{dp}{dx} = -\frac{q\sigma}{x^2},\\ \frac{dq}{dx} = \sigma x^2, \\ p(x) = \frac{\Pi^\gamma}{(4\pi)^{\gamma-1}}\sigma^{\gamma}. \end{array}$ (4.34)

gde Π_γ - tot zhe bezrazmernyi kompleks (4.32).

Sistema (4.34) dolzhna reshat'sya pri sleduyushih granichnyh usloviyah, zapisannyh v bezrazmernyh peremennyh:

$\begin{array}{l} x = 0, \, q = 0, \, p, \, \sigma - \mbox{ogranicheny},\\ x = 1, \, q = 1, \, p = \sigma = 0. \end{array}$ (4.35)

Ochevidno, chto uravneniya (4.34) i usloviya (4.35) yavlyayutsya tipichnoi zadachei na sobstvennye znacheniya. Reshenie etih uravnenii, udovletvoryayushih granichnym usloviyam (4.35), vozmozhno tol'ko pri opredelennom znachenii edinstvennogo chislennogo parametra Π_γ. Chislennoe reshenie sistemy (4.34) - (4.35) i pozvolyaet opredelyat' parametry Π_γ. Eti dannye privedeny v tabl. 1 (chislennye znacheniya kompleksov dlya drugih znachenii γ mozhno naiti v [5]):

Tablica 1

γ	3	2	5/3	3/2	4/3	5/4
$\Pi^\gamma$	2,270	0,637	0,424	0,365	0,364	0,477
$\frac{\sigma(0)}{3} = \frac{\rho_c}{\rho}$	1,836	3,290	5,991	11,043	54,183	622,408

V poslednei stroke tablicy privedeno otnoshenie central'noi plotnosti konfiguracii k ee srednei plotnosti - velichina, v tri raza men'shaya znacheniya bezrazmernoi funkcii σ(0) v centre konfiguracii.

To, chto my sdelali vyshe, i est' primenenie principa podobiya. Zvezdy s odinakovym indeksom politropy u imeyut odinakovoe stroenie, odinakovuyu koncentraciyu veshestva k centru. Radiusy zvezd raznyh mass, no postroennyh po odinakovoi politrope, opredelyayutsya po sootnosheniyu (4.32). Vazhno, chto primenenie principa podobiya pozvolilo opredelit' i chislennoe znachenie parametra Π_γ - v etom i proyavlyaetsya preimushestvo metoda podobiya pered prostym analizom razmernostei, primenimom v sluchae, kogda imeyutsya tochnye uravneniya, opisyvayushie samo yavlenie.

Svoistva politropnyh modelei neodnokratno issledovalis' samym obshim obrazom (sm., naprimer, rabotu [5]). Zdes' oni takzhe rassmatrivalis' v gl. 3, gde k poluchennym tam rezul'tatam mozhno teper' dobavit' znachenie chislennogo bezrazmernogo kompleksa Π_γ. V chastnosti, imeem sleduyushee tochnoe vyrazhenie dlya massy zvezdy s politropnym pokazatelem γ = 4/3 i dannoi politropnoi temperaturoi

$M_{4/3} = \left(\frac{K_{4/3}}{\Pi_{4/3}G}\right)^{3/2} = 4,6\left(\frac{K_{4/3}}{G}\right)^{3/2}.$ (4.36)

Iz chislennyh znachenii velichii Π_γ, privedennyh vyshe, sleduet, chto v oblasti γ ≈ 1,5 - 1,33 velichina Π_γ pochti ne menyaetsya pri izmenenii γ. Eto obstoyatel'stvo pozvolyaet sdelat' drugoi vazhnyi vyvod. Rassmotrim posledovatel'nost' politropnyh modelei, imeyushih odinakovuyu massu M₀, odinakovoe znachenie K_γ, no razlichnye znacheniya γ v nebol'shom intervale 1,35 < γ < 1,5. Zdes' pochti odinakovy i Π_γ. Takuyu posledovatel'nost' vsegda mozhno osushestvit', poskol'ku pri γ ≠ 4/3 massa politropnoi modeli mozhet byt' proizvol'noi. Posmotrim teper', kak menyaetsya radius u etoi posledovatel'nosti modelei pri umen'shenii γ . Iz (4.36) sleduet:

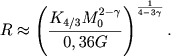
$R \approx \left(\frac{K_{4/3} M_0^{2-\gamma}}{0,36G}\right)^{\frac{1}{4-3\gamma}}.$ (4.37)

Budem teper' priblizhat' γ k 4/3. Pokazatel' 1/(4-2γ) stremitsya k -∞, a velichina v skobkah ostaetsya bol'shei edinicy, esli M₀ > M_4/3. Otsyuda sleduet, chto radiusy takih modelei stremyatsya k nulyu. Eto i est' dokazatel'stvo kollapsa zvezdnyh modelei s massoi, bol'shei predela (4.36), pri stremlenii pokazatelya γ k 4/3 sverhu.

Pereidem teper' k rassmotreniyu modelei polnost'yu konvektivnyh zvezd. Kak pravilo, konvektivnyi perenos energii imeet mesto v otnositel'no holodnyh zvezdah, gde β ≈ 1 i gde poetomu γ = 5/3. Eto uslovie budem schitat' vypolnennym. Velichina K_5/3 v politropnoi otnoshenii r=K_5/3ρ^5/3 zavisit ot entropii gaza, kotoraya schitaetsya postoyannoi po vsei masse zvezdy. Napomnim, chto my predpolagaem konvekciyu adiabaticheskoi. No luchshe parametr K_5/3 vyrazit' cherez central'nuyu temperaturu zvezdy T_c. Uchtem takzhe, chto central'naya plotnost' politropy s γ = 5/3 bol'she srednei v 5,991 raz. Imeem

$K_{5/3} = \frac{\Re}{\mu}\frac{T_c}{\rho_c^{5/3}} = 1,62\frac{\Re}{\mu}\frac{T_c R^2}{M^{2/3}}.$ (4.38)

Vozvrashayas' k osnovnomu sootnosheniyu (4.32), poluchaem svyaz' mezhdu tremya osnovnymi parametrami M, R i T:

$\frac{\Re T_c}{\mu}\frac{R}{GM} = 0,260.$ (4.39)

Esli schitat' massu zvezdy zadannoi, to odnogo sootnosheniya (4.39) nedostatochno dlya opredeleniya radiusa ili central'noi temperatury zvezdy. Neobhodimy dopolnitel'nye svyazi, kotorye dolzhny vklyuchat' i novye parametry, harakterizuyushie zvezdu.

Ochevidno, chto takim parametrom dolzhna byt' svetimost', takzhe harakterizuyushaya central'nuyu temperaturu zvezdy. Predpolozhim, chto istochniki energii opisyvayutsya obshim sootnosheniem (4.24). Raspredelenie plotnosti i temperatury v zvezde zadano usloviem konvektivnogo perenosa energii i poetomu dostatochno vychislit' prosto pervyi integral (4.15) pri r ≈ R. Perehodya k bezrazmernym peremennym (4.33) i uchityvaya, chto

$\frac{T}{T_c} = \left(\frac{\rho}{\rho_c}\right)^{2/3} = \left(\frac{\sigma}{\sigma(0)}\right)^{2/3},$

nahodim

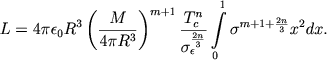
$L = 4\pi \epsilon_0 R^3 \left(\frac{M}{4\pi R^3}\right)^{m+1}\frac{T_c^n}{\sigma_{\epsilon}^{\frac{2n}{3}}}\int\limits_0^1 \sigma^{m+1+\frac{2n}{3}}x^2dx.$ (4.40)

Stepen' m + 1 + 2n/Z dostatochno velika u vseh tipov termoyadernyh reakcii. Poetomu vydelenie energii sosredotocheno tol'ko v nebol'shom ob'eme vblizi centra zvezdy. Eto oznachaet, chto mozhno vychislit' integral v (4.40), vospol'zovavshis' podhodyashei approksimaciei σ(h) pri x → 0. Udobnym sootnosheniem, spravedlivym dlya politropy s lyubym pokazatelem, yavlyaetsya formula

$\sigma = \sigma(0)e^{-\frac{x^2}{6}},$ (4.41)

kotoraya udovletvoryaet takzhe neobhodimomu usloviyu dσ/dx = 0 pri x=0. Podstavlyaya (4.41) v (4.40), nahodim okonchatel'no:

$L = \epsilon_0 \left(\frac{6\pi}{m+1+\frac{2n}{3}}\right)^{3/2} \left(\frac{\sigma(0)}{4\pi}\right)^{m+1} \frac{M^{m+1}}{R^{3m}}T_c^n.$ (4.42)

Eto i est' iskomoe vyrazhenie svetimosti cherez M, R i T_c. Isklyuchaya iz (4.42) i (4.39) central'nuyu temperaturu T_c, poluchim odno sootnoshenie mezhdu M, L i R. Eta formula imeet vid

$L = \epsilon_0 \left(\frac{6\pi}{m+1+\frac{2n}{3}}\right)^{3/2} \left(\frac{3}{2\pi}\right)^{m+1} (0,26)^n \left(\frac{G\mu}{\Re}\right)^{n} \frac{M^{m+n+1}}{R^{3m+n}}.$ (4.43)

U holodnyh zvezd s konvektivnym perenosom osnovnym istochnikom energii yavlyaetsya protonnaya reakciya pri n ≈ 6 i m = 1. Togda iz (4.43) imeem

$L \sum \frac{M^8}{R^9}.$

Vtoroe sootnoshenie, svyazyvayushee eti tri parametra, mozhet byt' polucheno iz analiza uslovii v zvezdnyh atmosferah. Priblizhenno eto sdelat' trudno, dazhe vypolnenie chislennyh raschetov na EVM svyazano s preodoleniem mnogih slozhnyh problem. Poetomu my zdes' ne budem etim zanimat'sya. Krome togo, predpolozhenie o polnost'yu konvektivnoi modeli yavlyaetsya daleko idushei idealizaciei. Teoreticheskie raschety dayut dlya holodnyh zvezd-karlikov zavisimost' L ∼ M^1,7, no u nih imeyutsya i oblasti s luchistym perenosom energii.

Neskol'ko bolee podrobno modeli zvezd, v tom chisle i teh iz nih, gde sushestvenna rol' konvektivnogo perenosa energii, obsuzhdayutsya v poslednem paragrafe etoi glavy.

<< § 4.1 Osnovnye uravneniya teorii vnutrennego stroeniya zvezd | Oglavlenie | § 4.3 Belye karliki i neitronnye zvezdy >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce