Astronet > Razmernosti i podobie astrofizicheskih velichin

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 4.2 Politropnye i konvektivnye zvezdy | Oglavlenie | § 4.4 Zvezdy s luchistym perenosom energii >>

§ 4.3 Belye karliki i neitronnye zvezdy

Rassmotrim teper' usloviya podobiya zvezd, postroennyh iz vyrozhdennogo elektronnogo gaza. Kak uzhe podcherkivalos', vse politropnye zvezdy s odinakovym indeksom politropy podobny po svoemu stroeniyu. Uravnenie sostoyaniya vyrozhdennogo elektronnogo gaza budet strogoi politropoi, esli, vo-pervyh, vtorye chleny v (4.9) ili (4.10) maly, t. e. v predele, kogda po vsemu ob'emu zvezdy vyrozhdennyi elektronnyi gaz yavlyaetsya polnost'yu nerelyativistskim libo polnost'yu relyativistskim, i, vo-vtoryh, temperaturnymi popravkami mozhno prenebrech', t. e. maly i vtorye chleny v (4.5) i v (4.6) pochti po vsei masse belogo karlika.

V predele polnost'yu nerelyativistskogo vyrozhdennogo elektronnogo gaza, t. e. pri uslovii

$\frac{3M}{4\pi R^3} = \bar\rho \ll \frac{7^{3/2}}{3\pi^2} \left(\frac{m_e c}{\hbar}\right)^{3} m_p \mu_e,$ (4.44)

sostoyanie gaza opisyvaetsya politropoi s γ = 5/3 i my poluchaem iz (4.32) bolee tochnoe vyrazhenie, chem (3.46):

$R = \frac{(3\pi)^{2/3}}{5 \cdot 0,424}\frac{\hbar^2}{m_e(\mu_e m_p)^{5/3}}\frac{1}{GM^{1/3}} = \frac{2,8 \cdot 10^9}{\mu_e^{5/3}}\left(\frac{M_\odot}{M}\right)^{1/3}\mbox{sm}.$ (4.45)

Iz (4.44) i (4.45) sleduet, chto nerelyativistskimi belymi karlikami yavlyayutsya zvezdy s otnositel'no nebol'shoi massoi (kak pokazyvayut ocenki, M≲ 2μ_e^-2M_☉ ≈ 0,5M_☉ ). Po mere uvelicheniya massy vyrozhdennyi elektronnyi gaz stanovitsya relyativistskim snachala v centrah konfiguracii, a zatem, po mere perehoda k bol'shim massam, relyativizaciya ohvatyvaet i zametnuyu chast' massy zvezdy. Struktura ee pri etom menyaetsya i postepenno perehodit k strukture politropy s γ = 4/3. Pri takom perehode kazhdoi masse sootvetstvuet svoya konfiguraciya (oni byli rasschitany Chandrasekarom [5]), no belye karliki s bol'shei relyativizaciei elektronov opyat' stanovyatsya podobnymi v sootvetstvii s politropoi γ = 4/3.

Uravnenie politropy relyativistskogo vyrozhdennogo elektronnogo gaza dano formuloi (4.6). Poetomu uslovie (4.36), opredelyayushee massu zvezdy s politropoi γ = 4/3, priobretaet vid

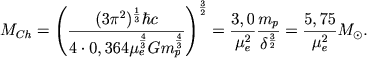
$M_{Ch} = \left(\frac{(3\pi^2)^{\frac{1}{3}}\hbar c}{4 \cdot 0,364 \mu_e^{\frac{4}{3}}G m_p^{\frac{4}{3}}}\right)^{\frac{3}{2}} = \frac{3,0}{\mu_e^2}\frac{m_p}{\delta^{\frac{3}{2}}} = \frac{5,75}{\mu_e^2}M_{\odot}.$ (4.46)

Itak, vse belye karliki, postroennye iz vyrozhdennogo relyativistskogo elektronnogo gaza, imeyut pochti odnu i tu zhe massu, podobnoe stroenie i ochen' malyi radius. Soglasno (4.10) i (4.37) radius belogo karlika umen'shaetsya s rostom central'noi plotnosti kak R ∼ exp(-const ⋅ ρ_c^2/3). Massa (4.46) est' predel'naya massa belogo karlika, tak nazyvaemyi chandrasekarovskii predel, kotoryi my uzhe obsuzhdali v gl. 3. Sleduet otmetit', chto sushestvovanie predela mass vyrozhdennyh zvezd bylo pokazano sovetskimi fizikami L. D. Landau i M. P. Bronshteinom v bolee rannih rabotah, chem eto bylo sdelano Chandrasekarom.

Razumeetsya, struktura belyh karlikov ne opredelyaetsya tol'ko prostymi politropnymi sootnosheniyami ili dazhe bolee obshim vyrazheniem dlya uravneniya sostoyaniya vyrozhdennogo elektronnogo gaza (3.39) - (3.40). Naprimer, struktura belyh karlikov s bol'shoi plotnost'yu dolzhna rasschityvat'sya s uchetom effektov obshei teorii otnositel'nosti. Sushestvennoe vliyanie pa ih strukturu okazyvaet bystroe vrashenie. Vazhnoe znachenie imeyut i kristallicheskie svoistva gaza atomnyh yader v nedrah belyh karlikov, kak eto vpervye bylo otmecheno D. A. Kirzhnicem. My ne budem obsuzhdat' vse eti svoistva belyh karlikov, dlya pas vazhna byla lish' ta chast' teorii, kotoraya rassmatrivaet podobie belyh karlikov po krainei mere v pervom priblizhenii. Obzor issledovanii po razlichnym effektam, vliyayushim pa strukturu i svoistva belyh karlikov, mozhno naiti v knigah Shacmana [12], G. S. Saakyana [13] i stat'e Mestela v sbornike [9].

Energetika belyh karlikov i ih svetimost' tesno svyazany s evolyuciei etih zvezd. K etomu zhe krugu voprosov otnosyatsya i issledovaniya nedavno obnaruzhennyh sil'nyh magnitnyh polei u nekotoryh belyh karlikov. V.se eti problemy, strogo govorya, vyhodyat za ramki nastoyashei knigi, no nekotorye raschety izmeneniya svetimosti so vremenem uzhe byli rassmotreny v gl. 3.

Princip podobiya mozhno primenit' k issledovaniyu stroeniya belyh karlikov i pri uchete temperaturnyh effektov, esli schitat', chto v osnovnoi masse vyrozhdennogo gaza temperatura T_d, pochti postoyanna. Eto bolee ili menee spravedlivo v silu ochen' horoshei teploprovodnosti vyrozhdennogo elektronnogo gaza. Esli podstavit' uravneniya sostoyaniya (4.5) ili (4.6) v pervye dva uravneniya (4.31) pri T = T_d = const, to poluchim pri preobrazovanii (4.33) takzhe pervye dva uravneniya (4.34). Izmenitsya tol'ko svyaz' mezhdu bezrazmernymi davleniem i plotnost'yu. Vmesto opredeleniya davleniya kak $p = \frac{\Pi_\gamma}{(4\pi)^{\gamma - 1}}\sigma^\gamma$ , teper' budem imet' sootnosheniya

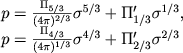
$\begin{array}{l} p = \frac{\Pi_{5/3}}{(4\pi)^{2/3}}\sigma^{5/3} + \Pi'_{1/3} \sigma^{1/3},\\ p = \frac{\Pi_{4/3}}{(4\pi)^{1/3}}\sigma^{4/3} + \Pi'_{2/3} \sigma^{2/3} \end{array}$ (4.47)

dlya nerelyativistskogo i relyativistskogo belyh karlikov sootvetstvenno. Zdes' P'_1/3 i P'_2/3 - novye bezrazmernye kompleksy, opredelennye vyrazheniyami

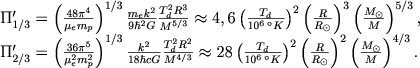
$\begin{array}{l} \Pi'_{1/3} = \left(\frac{48 \pi^4}{\mu_e m_p}\right)^{1/3} \frac{m_e k^2}{9\hbar^2 G} \frac{T_d^2 R^3}{M^{5/3}} \approx 4,6\left(\frac{T_d}{10^6 \,^\circ K}\right)^2 \left(\frac{R}{R_\odot}\right)^3 \left(\frac{M_\odot}{M}\right)^{5/3} ,\\ \Pi'_{2/3} = \left(\frac{36 \pi^5}{\mu_e^2 m_p^2}\right)^{1/3} \frac{k^2}{18\hbar c G} \frac{T_d^2 R^2}{M^{4/3}} \approx 28\left(\frac{T_d}{10^6 \,^\circ K}\right)^2 \left(\frac{R}{R_\odot}\right)^2 \left(\frac{M_\odot}{M}\right)^{4/3} . \end{array}$ (4.48)

Bezrazmernye kompleksy P_5/3 i P_4/3 po-prezhnemu opredelyayutsya formuloi (4.32), gde vmestoK_5/3 i K_4/3 sleduet podstavit' sootvetstvuyushie konstanty iz uravneniya sostoyaniya vyrozhdennogo elektronnogo gaza pri T → 0.

Temperaturnye dobavki v (4.5) ili (4.6) uchityvayut teplovoe dvizhenie elektronov. No nekotoryi vklad v polnoe davlenie vnosit i teplovoe dvizhenie nevyrozhdennyh yader. Ne budem vypisyvat' polnoe vyrazhenie dlya vseh popravok; privedem lish' formulu dlya sluchaya, kogda sushestvenno tol'ko davlenie vyrozhdennogo elektronnogo gaza i gaza atomnyh yader. Etot sluchai vstrechaetsya pri otnositel'no nizkih temperaturah, kogda ochen' maly temperaturnye dobavki v (4.5) ili (4.6), proporcional'nye T². Vyrazhenie dlya davleniya v bezrazmernyh peremennyh imeet vid

$p = \frac{\Pi_\gamma}{(4\pi)^{\gamma - 1}}\sigma^\gamma + \Pi'_1\sigma,$ (4.49)

gde P'₁ - novyi bezrazmernyi kompleks, ne zavisyashii ot usloviya relyativizacii elektronov:

$\Pi'_1 = \frac{k}{\mu_d m_p G}\frac{T_d R}{M} = \frac{0,043}{\mu_d}\frac{R}{R_\odot}\frac{M_\odot}{M} \frac{T_d}{10^6 \,^\circ K}.$ (4.50)

Nado takzhe imet' v vidu, chto, v otlichie ot (4.48), gde velichina μ_e est' molekulyarnyi ves, prihodyashiisya na odin elektron (poetomu μ_e blizko k dvum), μ_e v (4.50) est' atomnyi molekulyarnyi ves (dlya zheleznogo belogo karlika μ_e ≈ 56).

Esli temperatura vnutri belogo karlika poryadka desyatkov millionov .gradusov, to bezrazmernye kompleksy (4.48) i (4.50) mnogo men'she edinicy, poskol'ku radiusy belyh karlikov mnogo men'she radiusa Solnca. No pa nachal'nom etape ih evolyucii eti parametry mogut byt' i bol'shimi.

Dlya opredeleniya struktury belyh karlikov s uchetom temperaturnyh effektov (v predpolozhenii izotermichnosti) sleduet reshat' sistemu (4.34) sovmestno s (4.47) ili (4.49) pri teh zhe granichnyh usloviyah (4.35). Pravda, poslednie zdes' stanovyatsya netochnymi, poskol'ku uslovie izotermichnosti zavedomo nespravedlivo dlya naruzhnyh oblastei belyh karlikov. Ih mozhno vidoizmenit' tak, chtoby uchest' i padenie temperatury vo vneshnih sloyah.

Reshenie sistemy (4.34) teper' opredelyaet svyaz' mezhdu parami bezrazmernyh kompleksov: P_5/3 i P'_4/3; P_4/3 i P'_2/3; P_5/3 i P'₁; P_4/3 i P'₁. Eto oznachaet, chto v etom sluchae my nahodim svyaz' mezhdu tremya parametrami - massoi belogo karlika, ego radiusom i vnutrennei temperaturoi kak dlya sluchaya nerelyativistskogo belogo karlika, tak i dlya relyativistskogo s massoi vblizi verhnego predela, no eshe imeyushego konechnyi radius.

Chislennoe reshenie uravnenii (4.34) s uravneniyami sostoyaniya vyrozhdennogo gaza, uchityvayushimi temperaturnye effekty, bylo polucheno G. M. Zhislinym i V. I. Petruhinoi. Predpolagalas' izotermichnost' vplot' do sostoyaniya, gde temperaturnye chleny v tri raza men'she davleniya vyrozhdennogo gaza. V sloyah, blizkih k poverhnosti, davlenie approksimirovalos' stepennoi formuloi, uchityvayushei nepreryvnost' davleniya i plotnost'. Rezul'taty resheniya privedeny v tabl. 2.

Tablica 2

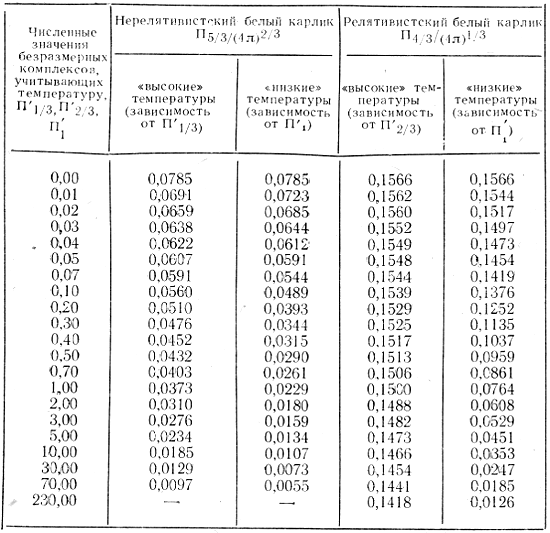
Zdes' uslovno sluchaem "vysokih temperatur" nazvano ispol'zovanie uravneniya sostoyaniya (4.47), a sluchaem "nizkih temperatur" - uravneniya sostoyaniya (4.49). Real'noe znachenie imeyut velichiny bezrazmernyh kompleksov P'_1/3, P'_2/3, P'₁ men'she edinicy, no raschety provedeny i dlya bol'shih' znachenii etih kompleksov dlya togo, chtoby prosledit' sootnoshenie mezhdu kompleksami na bol'shem intervale velichin.

Pol'zovat'sya etoi tablicei mozhno sleduyushim obrazom. Rassmotrim dlya primera nerelyativistskii belyi karlik s uravneniem sostoyaniya (4.47). Pervyi stolbec tablicy daet funkcional'nuyu zavisimost' $\Pi_{5/3} = \phi(\Pi'_{1/3})$ kotoruyu mozhno perepisat' v vide $\frac{A}{M^{1/3}R} = \phi\left(B\frac{R^3T_d^2}{M^{5/3}}\right)$ , gde A i V - postoyannye, vyrazhennye cherez parametry uravneniya sostoyaniya. Reshaya eto uravnenie (naprimer, graficheski), mozhno naiti, kak menyaetsya radius belogo karlika po mere izmeneniya ego vnutrennei temperatury.

Rassmatrivaya tablicu, mozhno ubedit'sya, chto poka P'_1/3 i P'₁ maly, izmeneniya radiusa belyh karlikov s temperaturoi neveliki. Uravneniya sostoyaniya (4.49) daet neskol'ko bol'shii effekt. Lyubopytno, chto uvelichenie temperatury umen'shaet radius belogo karlika. Eto svyazano s tem, chto dobavka teplovoi energii dolzhna v ramkah teoremy viriala uvelichit' absolyutnoe znachenie potencial'noi energii.

Pri znachenii bezrazmernyh kompleksov P'_1/3 i P'₁, sravnimyh s edinicei, izmeneniya radiusov stanovyatsya bolee zametnymi, hotya, konechno, predstavlenie real'nogo uravneniya sostoyaniya v vide politropy s malymi temperaturnymi dobavkami stanovitsya vse bolee grubym. No dlya polukachestvennyh ocenok mozhno ispol'zovat' i eti znacheniya bezrazmernyh kompleksov.

V sluchae relyativistskih belyh karlikov zavisimost' P_4/3 i P'₁ i osobenno ot P'_2/3 vyrazhena znachitel'no slabee. Poskol'ku zdes' P_4/3 opredelyaet tol'ko massu belogo karlika $m_{4/3} \sim \Pi_{4/3}^{3/2}$ , to uvelichenie T_d ekvivalentno uvelicheniyu predel'noi massy relyativistskogo belogo karlika. Teplovaya energiya trebuet uvelicheniya absolyutnogo znacheniya potencial'noi energii putem sootvetstvuyushego izmeneniya massy (takzhe v sootvetstvii s teoremoi viriala). Hotya sootvetstvuyushie izmeneniya massy i neveliki, no oni mogut sygrat' sushestvennuyu rol' v evolyucii zvezd vblizi chandrasekarovskogo predela.

Nakonec sformuliruem kriterii podobiya struktury belogo karlika s uchetom temperaturnyh effektov. Budem nazyvat' struktury belyh karlikov podobnymi, esli vse opredelyayushie kompleksy odinakovy. U nerelyativistskih belyh karlikov kriterii podobiya trebuet vypolneniya uslovii: $RM^{1/3} = const$ , $T^2_d R^3 M^{-5/3} = const$ , libo $T_d R M^{-1} = const$ , otkuda takzhe sleduet $T_d M^{-4/3} = const$ kak dlya uravnenii sostoyaniya (4.47), tak i dlya (4.49)). V sluchae relyativistskih belyh karlikov usloviya podobiya drugie. Massa fiksirovana znacheniem P_4/3, a iz (4.48) i (4.50) sleduet, chto podobny struktury belyh karlikov s temperaturnymi popravkami, esli $T_d R = const$ .

Nakonec, rassmotrim sluchai konfiguracii, sostoyashih iz vyrozhdennogo neitronnogo gaza. V pervom priblizhenii neitronnye zvezdy podobny belym karlikam, poskol'ku uravneniya sostoyaniya razlichayutsya lish' raznymi znacheniyami velichiny K_γ.

Esli dopustit', chto zvezda sostoit tol'ko iz nerelyativistskogo neitronnogo gaza i prenebrech' silami yadernogo vzaimodeistviya mezhdu neitronami, to vse razlichie so sluchaem nerelyativistskih belyh karlikov svodilos' by k zamene m_e i m_p na massu neitrona m_n i usloviyu μ_e = 1. Naprimer, soglasno (3.45) radius neitronnoi zvezdy men'she radiusa belogo karlika na mnozhitel', ravnyi otnosheniyu massy elektrona k masse neitrona, t. e.

$R = \frac{(3\pi^2)^{2/3}}{5 \cdot 0,424}\frac{\hbar^2}{Gm_n^{8/3}M^{1/3}} = 15 \left(\frac{M_\odot}{M}\right)^{1/3} \mbox{km},$ (4.51)

a predel'naya massa relyativistskoi neitronnoi zvezdy ravnyalas' by 5,75 M_☉.

Real'naya kartina, odnako, slozhnee. Vo-pervyh, neobhodim uchet vzaimodeistviya mezhdu neitronami. Vo-vtoryh, vsegda v neitronnom gaze imeetsya primes' protonov i elektronov, kotoryh obychno ne men'she 4-5%. V-tret'ih, blizkie k poverhnosti sloi neitron noi zvezdy sostoyat iz obychnogo veshestva, t. e. iz elektronov i atomnyh yader. Chastichno eto veshestvo nahoditsya v kristallicheskom sostoyanii, a chastichno predstavlyaet soboi plazmu. Atomnyi ves yader etogo veshestva menyaetsya, uvelichivaetsya po mere pogruzheniya v glub' neitronnoi zvezdy i lish' postepenno proishodit perehod k preimushestvenno neitronnomu sostoyaniyu. V central'nyh chastyah bolee massivnyh neitronnyh zvezd imeyutsya i giperony.

Takim obrazom, politropnaya zavisimost' mozhet rassmatrivat'sya tol'ko kak pervoe, ochen' gruboe priblizhenie k real'nomu uravneniyu sostoyaniya neitronnogo gaza. Bylo provedeno neskol'ko raschetov uravnenii sostoyaniya holodnogo (t. e. pri T = 0) neitronnogo gaza. Odno iz nih, poluchennoe Kanuto [14], privedeno na ris. 2. Kasatel'naya sootvetstvuet zavisimosti r ∼ ρ^5/3. Mozhno otmetit' sleduyushie osobennosti. Esli isklyuchit' oblast' otnositel'no nizkih plotnostei, gde primes' neitronov mala, v oblasti umerennyh i bol'shih plotnostei zavisimost' r ∼ ρ^5/3 v pervom priblizhenii vypolnyaetsya. Dazhe v oblasti plotnostei, bol'shih yadernoi, r ≳ 10¹⁵ g\sm³, ne vidno perehoda k relyativistskoi zavisimosti r ∼ ρ^4/3. Zdes' tol'ko umen'shaetsya parametr K_5/3. Velichina etogo parametra dlya neitronnyh zvezd s tipichnoi srednei plotnost'yu poryadka 10¹⁰-10¹⁴ g/sm³

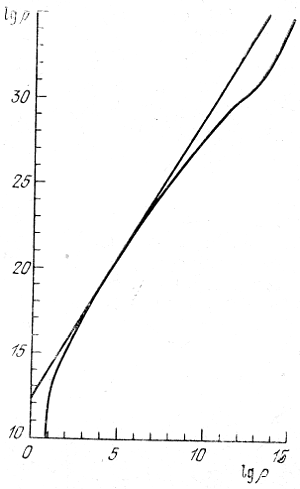
Ris. 2. Uravnenie sostoyaniya neitronnogo gaza soglasno Kanuto. Kasatel'naya pryamaya sootvetstvuet zavisimosti r ∼ ρ^5/3.

blizka k $K_{5/3} \approx 10^{10} \frac{\mbox{din}}{\mbox{sm}^2} \cdot \frac{\mbox{sm}^5}{\mbox{g}^{3/5}}$ . Podstavlyaya eto znachenie v sootnoshenie (4.32), nahodim dlya radiusa neitronnyh zvezd:

$R = \frac{10^{10}}{0,424G}\frac{1}{M^{1/3}} \approx 28\left(\frac{M_\odot}{M}\right)^{1/3} \mbox{km},$ (4.52)

t. e. vsego v dva raza bol'she, chem v idealizirovannom sluchae (4.51). U neitronnyh zvezd s maloi massoi radius mozhet byt', veroyatno, mnogo bol'she. Zdes', s odnoi storony, uvelichivaetsya mnozhitel' M^-1/3, a s drugoi storony, vozrastaet i parametr K_5/3, poskol'ku men'she srednie plotnosti. Krome togo, velik i vklad sloev, sostoyashih iz obychnogo veshestva. V poslednee vremya bylo provedeno neskol'ko raschetov konkretnyh modelei neitronnyh zvezd. My ne budem ih obsuzhdat', poskol'ku nas v osnovnom interesuyut voprosy podobiya modelei. Estestvenno, chto utochnennye raschety dayut slozhnuyu zavisimost' R(M), kotoraya k tomu zhe eshe ne poluchena s dostatochnoi uverennost'yu.

Kak otmechalos' v gl. 3, verhnii predel massy neitronnyh zvezd opredelyalsya iz usloviya relyativistskogo vyrozhdeniya neitronnogo gaza (predel Oppengeimera - Volkova). Iz ris. 2 sleduet, chto etot predel sootvetstvuet perehodu k ochen' bol'shim plotnostyam, poka nedostupnym dlya bolee ili menee strogogo teoreticheskogo rascheta uravneniya sostoyaniya. Poetomu luchshe ocenit' verhnii predel massy neitronnoi zvezdy tak, kak eto sdelano v formule (3.53), potrebovav, chtoby radius neitronnoi zvezdy ne prevyshal gravitacionnogo radiusa. Dlya modeli ideal'nogo neitronnogo gaza, ispol'zuya opredelenie (4.51), nahodim

$M \lesssim 5^{3/4}M_\odot \simeq 3M_\odot.$

Uchet real'nogo uravneniya sostoyaniya neskol'ko uvelichivaet etot predel. Ispol'zuya podobnym obrazom formulu (4.52), poluchaem dlya. predela massy neitronnyh zvezd:

$28\left(\frac{M_\odot}{M}\right)^{1/3} \ge \frac{2GM}{c^2} = 3\frac{M}{M_\odot}, \quad M \le 5,2M_\odot.$ (4.53)

Esli potrebovat', chtoby radius neitronnoi zvezdy byl bol'she, naprimer, 3R_g, to predel massy budet nizhe na mnozhitel' 3^3/4 ≈ 2,2.

Pri raschete ochen' plotnyh konfiguracii uravneniya gidrostaticheskogo ravnovesiya v n'yutonovskoi forme stanovyatsya neprimenimymi. V ramkah obshei teorii otnositel'nosti uravnenie gidrostaticheskogo ravnovesiya imeet vid (3.53), potrebovav, chtoby radius neitronnoi zvezdy ne prevyshal gravitacionnogo radiusa. Dlya modeli ideal'nogo neitronnogo gaza, ispol'zuya opredelenie (4.51), nahodim

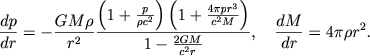
$\frac{dp}{dr} = -\frac{GM\rho}{r^2}\frac{\left(1+\frac{p}{\rho c^2}\right)\left(1+\frac{4\pi p r^3}{c^2 M}\right)}{1-\frac{2GM}{c^2 r}}, \quad \frac{dM}{dr} = 4\pi\rho r^2.$

V takom vide k etomu uravneniyu uzhe trudno (hotya i vozmozhno) primenyat' metody analiza razmernostei i podobiya. Zdes' my etogo delat' ne budem, no otmetim odno lyubopytnoe svoistvo etogo uravneniya (sm. [15]). Esli schitat' vse vtorye chleny v skobkah malymi po sravneniyu s edinicei, to poluchim

$\frac{dp}{dr} = \frac{GM\rho}{r^2}\left\{1 + \left( \frac{p}{\rho c^2} + \frac{4\pi p r^3}{c^2 M} + \frac{2GM}{c^2 r} + ...\right)\right\}.$

Kazhdyi iz chlenov v krugloi skobke zametno menyaetsya na protyazhenii vsego radiusa konfiguracii, no ih summa menyaetsya sushestvenno medlennee. V centre konfiguracii kruglaya skobka vsegda ravna 4r_s/ρ_ss², gde r_s i ρ_s - central'nye davlenie i plotnost'. Po mere perehoda k poverhnosti velichina krugloi skobki menyaetsya vsegda na neskol'ko desyatkov procentov dazhe v sluchae konfiguracii s ochen' bol'shoi koncentraciei k centru. Otsyuda sleduet metod, predlozhennyi v rabote [15] dlya ucheta effektov obshei teorii otnositel'nosti: mozhno rasschityvat' stroenie plotnoi zvezdy, pol'zuyas' n'yutonovskimi uravneniyami gidrostaticheskogo ravnovesiya, no zamenyaya postoyannuyu N'yutona G na "effektivnuyu velichinu gravitacionnogo vzaimodeistviya"

$G' = G\left(1+\frac{4p_c}{\rho_c c^2}\right).$

Dlya verhnei tochki grafika ris. 2 poluchaem G' = 1,4G. Predel massy neitronnyh zvezd proporcionalen G^-3/2, poetomu uchet effektov obshei teorii otnositel'nosti ponizhaet etot predel kak $\left(1+\frac{4p_c}{\rho_c c^2}\right)^{-3/2}$ . Dlya maksimal'noi plotnosti na grafike ris. 2 poluchim umen'shenie predel'noi massy do znacheniya M ≤ 3,ZM_☉, ili eshe men'she, esli R > 3R_☉. Vozmozhno, chto verhnii predel mass neitronnyh zvezd ne bol'she 2M_☉.

<< § 4.2 Politropnye i konvektivnye zvezdy | Oglavlenie | § 4.4 Zvezdy s luchistym perenosom energii >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce