Astronet > Razmernosti i podobie astrofizicheskih velichin

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 4.3 Belye karliki i neitronnye zvezdy | Oglavlenie | § 4.5 Chislennoe modelirovanie evolyucii zvezd >>

§ 4.4 Zvezdy s luchistym perenosom energii

Luchistyi perenos energii opredelyaet osnovnye svoistva i strukturu bol'shinstva zvezd. Pravda, veroyatno, voobshe net zvezd, v kotoryh po vsei ih masse energiya perenosilas' by tol'ko izlucheniem. V real'nyh usloviyah est' sloi i s luchistym i s konvektivnym perenosom. V otlichie ot konvekcii, potok energii, perenosimyi luchistoi teploprovodnost'yu, limitiruetsya velichinoi koefficienta neprozrachnosti. Poetomu zvezda kak by prisposablivaetsya k usloviyam perenosa energii izlucheniem, i ee struktura opredelyaetsya v pervuyu ochered' potokom luchistoi energii v teh sloyah, gde net konvekcii.

Zadacha zaklyuchaetsya v tom, chtoby, ispol'zuya etu osobennost' stroeniya zvezd, naiti kriterii podobiya i opredelit' svyazi mezhdu osnovnymi parametrami zvezdy. Razumeetsya, my ne budem rassmatrivat' v detalyah teoriyu vnutrennego stroeniya zvezd. V sootvetstvii s osnovnoi temoi knigi osnovnoe vnimanie udelyaetsya kriteriyam podobiya.

Voobshe govorya, nachalo razvitiya teorii vnutrennego stroeniya zvezd tozhe bylo svyazano s principom podobiya. Eshe v 1921 g. Eddington predpolozhil, chto vse zvezdy postroeny po odnoi, nazvannoi im standartnoi, modeli, opisyvaemoi politropoi s indeksom n=3. Schitalos', chto parametr β iz (4.12) odinakov po vsei zvezde, t.e. r ∼ T⁴ ∼ ρ^4/3, a koefficient neprozrachnosti i moshnost' istochnikov energii podbiralis' tak, chtoby udovletvorit' etomu usloviyu. Itak, po standartnoi modeli vse zvezdy podobny, a razlichie ih mass i svetimostei opredelyaetsya razlichiem v znachenii parametra β - otnosheniya luchevogo davleniya k polnomu. Radius zvezdy v etoi modeli teoreticheski ne opredelen, poskol'ku, kak izvestno, v politrope s n = 3 radius ne zavisit ot massy. Iz formuly (4.12) pri zadannom β mozhno naiti velichinu K_4/3 dlya sootnosheniya r = K_4/3ρ^4/3, a sledovatel'no, po (4.36), i massu zvezdy s dannym β Okonchatel'nyi rezul'tat takov (sm., naprimer, [5]):

$M = \frac{8}{G^{3/2}}\left(\frac{\Re}{\mu}\right)^2\left[\frac{1-\beta}{a\beta}\right]^{1/2} = \frac{9,6}{\mu^2}\frac{(1-\beta)^{1/2}}{\beta^2}M_\odot.$ (4.54)

Sluchai β = ½ , gde M ≈ 50M_☉/μ², byl rassmotren v gl. 3, gde eta velichina prinimalas' blizkoi k verhnemu predelu mass. U zvezd maloi massy β blizko k edinice.

Na osnove etoi standartnoi modeli Eddingtonom bylo obnaruzheno i issledovano sootnoshenie massa - svetimost', a Stremgrenom bylo dano ob'yasnenie glavnoi posledovatel'nosti na diagramme Ressela - Gercshprunga. Ispol'zovanie standartnoi modeli bylo opravdano tem, chto v to vremya ne bylo nikakih dannyh ob istochnikah energii v zvezdah. Do sozdaniya teorii termoyadernyh istochnikov energii byli predlozheny i drugie modeli zvezd, takzhe osnovannye na principe podobiya. V chastnosti, sleduet otmetit' model' Koulinga, uchityvayushuyu v yavnom vide zakon poglosheniya Kramersa i predpolagayushuyu, chto istochniki energii raspolozheny v centre zvezdy. V etoi modeli imeetsya konvektivnoe yadro v centre s radiusom 16,9% i s massoi 14,5% ot radiusa i massy zvezdy. Kak my uvidim nizhe, eta model' s konvektivnym yadrom okazalas' dovol'no blizkoi k real'nym modelyam s termoyadernymi istochnikami energii.

Bolee polnyi analiz podobiya zvezdnyh modelei, osnovannyi na primenenii principa podobiya, poyavilsya uzhe posle sozdaniya teorii termoyadernyh istochnikov energii. Odnim iz pervyh bylo issledovanie L. I. Sedova ([16, 17]). Izlozhenie podobnogo analiza dano takzhe v knigah [1, 4]. Raschet struktury podobnyh modelei zvezd dan V. S. Imshennikom i D. K. Nadezhinym [18]. Sleduyushee nizhe izlozhenie osnovano na etih rabotah.

Zapishem eshe raz polnuyu sistemu uravnenii vnutrennego stroeniya zvezdy s uchetom vseh izvestnyh nam uslovii, predpolagaya luchistyi perenos energii:

$\left. \begin{array}{l} \frac{dp}{dr} = -\frac{GM(r)}{r^2}\rho, \quad \frac{dM}{dr} = 4\pi r^2\rho, \\ \\ \frac{d}{dr}\left[\frac{1}{3} aT^4\right] = -\frac{\varkappa L(r)}{4\pi r^2c}\rho, \, \frac{dL}{dr} = 4\pi r^2\rho\epsilon, \\ \\ p = \frac{\Re}{\mu}\rho T + \frac{1}{3}aT^4, \quad \mu = \mu(X, Y, Z),\\ \\ \varkappa = \varkappa_0\frac{\rho^{\alpha}}{T^\nu}, \quad \epsilon = \epsilon_0\rho^mT^n. \end{array} \right\}$ (4.55)

Esli zadany velichiny μ, ϰ₀ i ε₀, a takzhe osnovnye parametry zvezdy M, L i R, to eta sistema mozhet byt' reshena polnost'yu pri sleduyushih granichnyh usloviyah:

$\begin{array}{l} r = 0, \, M = 0, \, p, \, \rho - \mbox{konechny},\\ r = R, \, p = \rho = 0. \end{array}$ (4.56)

Sistema (4.55) - (4.56) spravedliva, esli ni v yadre zvezdy, ni vblizi ee poverhnosti net zon, v kotoryh energiya perenositsya konvekciei. Etot sluchai i rassmatrivalsya L. I. Sedovym ([17, 18]). Privedem zdes' sootnosheniya, poluchennye im iz soobrazhenii razmernosti i principa podobiya (no v drugih oboznacheniyah).

V zvezde s luchistym perenosom energii net peremeshivaniya veshestva i poetomu mozhno ozhidat', chto himicheskii sostav veshestva menyaetsya vdol' radiusa. V vyrazheniyah dlya ε i ϰ eto mozhno uchest' nekotorym izmeneniem pokazatelei α , ν , m i n, schitaya velichiny ϰ₀ i ε₀ postoyannymi, a v vyrazhenii dlya molekulyarnogo vesa mozhno predpolozhit' sushestvovanie zavisimosti

$\mu = \mu_0\rho^{1-\xi}T^{1-\eta},$ (4.57)

gde ξ i η - nekotorye postoyannye chisla. Vvedem teper' novye bezrazmernye peremennye pri pomoshi preobrazovaniya, obobshayushego (4.33):

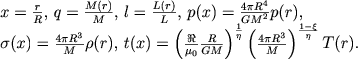
$\begin{array}{l} x = \frac{r}{R}, \, q = \frac{M(r)}{M}, \, l=\frac{L(r)}{L}, \, p(x) = \frac{4\pi R^4}{GM^2}p(r),\\ \sigma(x) = \frac{4\pi R^3}{M}\rho(r), \, t(x) = \left(\frac{\Re}{\mu_0}\frac{R}{GM}\right)^{\frac{1}{\eta}}\left(\frac{4\pi R^3}{M}\right)^{\frac{1-\xi}{\eta}}T(r). \end{array}$ (4.58)

Bolee slozhnoe preobrazovanie dlya temperatury opredelyaetsya neobhodimost'yu ucheta sootnosheniya (4.57). V drugih rabotah obychno prenebregaetsya izmeneniem molekulyarnogo vesa, i togda mozhno schitat' ξ = η = 1. Formula dlya perehoda ot T(r) k t(x) okazyvaetsya bolee prostoi.

Teper' zapishem uravneniya (4.55) v bezrazmernom vide:

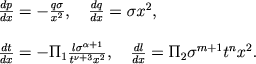
$\begin{array}{l} \frac{dp}{dx} = -\frac{q\sigma}{x^2}, \quad \frac{dq}{dx} = \sigma x^2,\\ \\ \frac{dt}{dx} = -\Pi_1\frac{l\sigma^{\alpha + 1}}{t^{\nu + 3}x^2},\quad \frac{dl}{dx} = \Pi_2\sigma^{m+1}t^n x^2. \end{array}$ (4.59)

Zdes' poyavilis' dva bezrazmernyh kompleksa:

$\Pi_1 = \frac{3\varkappa_0 L}{16\pi caR^2}\left(\frac{M}{4\pi R^3}\right)^{\alpha + 1 -\frac{\nu+3}{\eta}(1-\xi)} \left(\frac{\Re}{\mu_0}\frac{R}{GM}\right)^{\frac{\nu+3}{\eta}},$ (4.60)

$\Pi_2 = \frac{4\pi\epsilon_0 M}{L}\left(\frac{M}{4\pi R^3}\right)^{m + 1 + \frac{n}{\eta}(1-\xi)} \left(\frac{\mu_0}{\Re}\frac{GM}{R}\right)^{\frac{n}{\eta}},$ (4.61)

i vyrazhenie dlya polnogo davleniya, zapisannoe v bezrazmernom vide:

$p = \sigma^{\xi}t^{\eta} + \Pi_3t^4,$ (4.62)

gde eshe odin bezrazmernyi kompleks:

$\Pi_3 = \frac{a}{3}\left(\frac{\mu}{\Re}\frac{GM}{R}\right)^{\frac{4}{\eta}} \left(\frac{M}{4\pi R^3}\right)^{4\frac{1-\xi}{\eta}}\frac{4\pi R^4}{GM^2}.$ (4.63)

V chastnom sluchae postoyannogo molekulyarnogo vesa (ξ = η = 1) bezrazmernyi kompleks Π₃ zavisit tol'ko ot massy zvezdy:

$\Pi_3 = \frac{4\pi a}{3}\left(\frac{\mu_0}{\Re}\right)^4 G^3M^2 = \frac{4\pi^3}{45}\frac{\mu^4M^2}{m_p^2}\delta^2 = 0,78\mu_0^4\left(\frac{M}{M_\odot}\right)^2,$ (4.64)

gde, po-prezhnemu, δ = Gm_p²/ħc. Ochevidno, chto Π₃ harakterizuet otnositel'nuyu rol' luchevogo davleniya.

Nakonec, bezrazmernye granichnye usloviya budut imet' takoi vid:

$\begin{array}{l} x = 0, \, q = 0, \, l = 0, \, p, \, \sigma, \, t - \mbox{konechny},\\ x = 1, \, q = l = 1, \, p = \sigma = 0. \end{array}$ (4.65)

Takim obrazom, zadacha svelas' k resheniyu bezrazmernyh uravnenii (4.59) i (4.62) s granichnymi usloviyami (4.65). Reshenie harakterizuetsya tremya bezrazmernymi kompleksami: Π₁, Π₂, Π₃. Ochevidno, chto eti kompleksy mogli byt' polucheny i iz prostyh soobrazhenii razmernosti putem postroeniya matricy razmernosti dlya razmernyh opredelyayushih parametrov M, L, R, G, a, μ₀m_p/k, ϰ₀ i ε₀, harakterizuyushih zvezdu s luchistym perenosom energii i luchevym davleniem.

Odin iz treh kompleksov, naprimer, Π₃, dolzhen zadavat'sya proizvedeniem [h0M. Chislennye znacheniya kompleksov Π₁ i Π₂ togda budut polucheny pri reshenii sistemy (4.59) kak ee sobstvennye znacheniya. V rezul'tate mozhno naiti sootnosheniya Π₁ = ƒ(Π₃) i Π₂ = ƒ(Π₃), a sledovatel'no, i dve zavisimosti, naprimer, svetimosti zvezdy i radiusa zvezdy ot ee massy pri zadannyh znacheniyah razmernyh i bezrazmernyh (pokazateli stepeni) opredelyayushih parametrov.

V sluchae, kogda rol' luchevogo davleniya mala, t. e. otnositel'no mala massa zvezdy, mozhno prenebrech' luchevym davleniem, i togda bezrazmernye kompleksy Π₁ i Π₂ okazyvayutsya ne zavisyashimi ot Π₃. Pravda, bez resheniya sistemy (4.59) nam ne udastsya opredelit' ih chislennoe znachenie, no mozhno utverzhdat', chto oba eti kompleksa yavlyayutsya konstantami. Otsyuda i sleduyut dve zavisimosti svetimosti i radiusa zvezdy ot znacheniya ee massy, vpervye poluchennye L. I. Sedovym. Udobnee zapisat' eti sootnosheniya v logarifmicheskom vide (sm. [17]):

$\lg R = \frac{(2+\alpha+m)\eta-(4+\nu-n)(2-\xi)}{(4+3\alpha+3m)\eta+(4+\nu-n)(3\xi - 4)} \lg M + const,$ (4.66)

$\lg L = \left[1+m+\frac{2-\xi}{\eta}n+\frac{[(2+\alpha + m)\eta - (4+\nu - n)(2-\xi)][(3\xi - 4)n - 3m\eta]}{\eta[(4+3\alpha + 3m)\eta + (4+\nu -n)(3\xi-4)]}\right]\lg M + const.$ (4.67)

Chislennye znacheniya bezrazmernyh kompleksov Π₁ i Π₂ v rabotah [16, 17] ne opredelyalis', poetomu velichiny konstant v (4.66) i (4.67) ostalis' neizvestnymi.

Zadavayas' opredelennym vyborom parametrov α i ν , n i m, ξ i η, mozhno poluchit' stepennye zavisimosti L i R kak funkcii ot M. V prosteishem sluchae α = 1, ν = 7/2 (zakon Kramersa), m = 1, n = 4 (protonnyi cikl) i ξ = η = 1 imeem

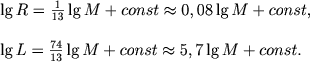
$\begin{array}{l} \lg R = \frac{1}{13}\lg M + const \approx 0,08 \lg M +const, \\ \\ \lg L = \frac{74}{13}\lg M + const \approx 5,7 \lg M +const. \end{array}$ (4.68)

To zhe samoe, no dlya uglerodnogo cikla (n=16) daet

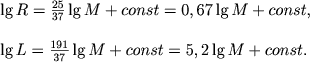
$\begin{array}{l} \lg R = \frac{25}{37}\lg M + const = 0,67 \lg M +const, \\ \\ \lg L = \frac{191}{37}\lg M + const = 5,2 \lg M +const. \end{array}$ (4.69)

Lyubopytno, chto sootnoshenie svetimost' - massa ochen' slabo zavisit ot harakteristik termoyadernyh reakcii. Kak uzhe podcherkivalos', eto svyazano s tem, chto struktura i svoistva zvezdy v pervuyu ochered' opredelyayutsya zakonom perenosi energii. No radius zvezdy sushestvenno zavisit ot vybora zakona vydeleniya energii. Dlya illyustracii rassmotrim i sluchai, kogda neprozrachnost' opredelyaetsya rasseyaniem na elektronah (sootnoshenie (4.21), t. e. α = ν = 0). Prenebregaya opyat' izmeneniem molekulyarnogo vesa, poluchim dlya vodorodnogo cikla (n=4):

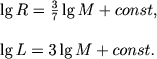
$\begin{array}{l} \lg R = \frac{3}{7}\lg M + const, \\ \\ \lg L = 3\lg M + const. \end{array}$ (4.70)

i dlya uglerodnogo cikla (n=16):

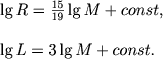
$\begin{array}{l} \lg R = \frac{15}{19}\lg M + const, \\ \\ \lg L = 3\lg M + const. \end{array}$ (4.71)

Zdes' istochniki energii voobshe ne vliyayut na sootnoshenie massa - svetimost'. Zametim, chto v etom sluchae my vernulis' k sootnosheniyu massa - svetimost' L ∼ M³, poluchennomu iz prostyh soobrazhenii razmernosti v gl. 3 (formuly (3.8) i (3.11)), takzhe v predpolozhenii nezavisimosti koefficienta neprozrachnosti ot plotnosti i temperatury.

Sravnenie s nablyudeniyami my provedem v sleduyushem paragrafe, gde rassmotrim rezul'taty chislennogo rascheta. Krome togo, nado podcherknut', chto v sootnosheniyah (4.66) - (4.71) ne uchteno vliyanie luchevogo davleniya.

Polnoe reshenie sistemy (4.59) - (4.65) dlya sluchaya odnorodnogo molekulyarnogo vesa (ξ = η = 1), no s uchetom luchevogo davleniya i konvektivnogo perenosa, bylo dano V. S. Imshennikom i D. K. Nadezhinym [18]. Eto reshenie pozvolilo opredelit' znacheniya bezrazmernyh kompleksov Π₁ i Π₂ dlya raznyh vyborov Π₃. Inymi slovami, v sootnosheniyah (4.66) i (4.67) byli polucheny znacheniya konstant i, bolee togo, byla opredelena zavisimost' etih konstant ot luchevogo davleniya. Eto oznachaet, chto, voobshe govorya, sootnoshenie svetimost' - massa opredelyaetsya ne tol'ko mnozhitelem pered lg M, v (4.67), no i zavisimost'yu konstanty ot massy, poyavlyayusheisya iz-za zavisimosti Π₂ ot Π₃.

Pri raschetah chislennyh znachenii bezrazmernyh kompleksov vazhno uchest' i vozmozhnost' obrazovaniya konvektivnyh yader v central'nyh oblastyah zvezd. Eto delaetsya sleduyushim obrazom. Tret'e uravnenie (4.59), opredelyayushee temperaturnyi gradient dt/dx spravedlivo tol'ko do teh por, poka velichina etogo gradienta ostaetsya men'she, chem adiabaticheskii gradient temperatury, naidennyi iz (4.13). Kak tol'ko gradient stanovitsya bol'shim, nastupaet konvekciya i tret'e uravnenie (4.59) stanovitsya neprimenimym. Vmesto etogo uravneniya teper' sleduet iz (4.13) i (4.1) opredelit' gradient temperatury v nedrah zvezdy pri perenose energii adiabaticheskoi konvekciei. Imeem

$\frac{dT}{dr} = \frac{\partial T}{\partial p}\frac{\partial p}{\partial r} = -\frac{\gamma - 1}{\gamma}\frac{GM\rho T}{pr^2}.$ (4.72)

V bezrazmernyh peremennyh (4.58)

$\frac{dt}{dx} = -\frac{2(4 - 3\beta)}{32 - 24\beta - 3\beta^2}\frac{q\sigma t}{px^2},$ (4.73)

gde velichina β (s sohraneniem peremennosti molekulyarnogo vesa)

$\beta = \frac{\sigma^\xi t^{\eta}}{\sigma^\xi t^{\eta} + \Pi_3 t^4} = \frac{1}{1+\Pi_3 t^{4-\eta}\sigma^{-\xi}}.$ (4.74)

Ochevidno, chto uchet konvektivnyh zon ne izmenit haraktera samoi zadachi nahozhdeniya sobstvennyh znachenii Π₁ i Π₂ pri zadannom Π₃. Ot nalichiya konvektivnyh zon zavisit tol'ko velichina chislennyh znachenii kompleksov. Poetomu sootnosheniya (4.66) - (4.71) s neopredelennymi znacheniyami postoyannyh spravedlivy kak dlya modelei bez konvektivnyh yader, tak i dlya modelei s konvektivnymi yadrami.

Itak, osnovnaya zadacha zaklyuchaetsya v nahozhdenii sobstvennyh znachenii sistemy uravnenii (4.59), gde v oblasti konvektivnogo yadra tret'e uravnenie (dlya dt/dx) zamenyaetsya na uravneniya (4.73) - (4.74). Granichnye usloviya dayutsya sootnosheniem (4.65).

Razumeetsya, analiticheskogo resheniya etoi zadachi net, mozhno poluchit' lish' chislennye resheniya. Izvestnoi trudnost'yu yavlyaetsya bol'shoe kolichestvo raznyh parametrov: α, ν , n, m, ξ i η i poetomu veliko chislo raznyh variantov resheniya.

V rabote V. S. Imshennika i D. K. Nadezhina [18] bylo rassmotreno neskol'ko variantov modelei s postoyannym po vsei zvezde molekulyarnym vesom, t. e. bylo prinyato uslovie ξ = η = 1.

V tabl. 3 privedeny harakteristiki nekotoryh iz rasschitannyh v [18] modelei. Zadavalos' znachenie kompleksa Π₃, kotoryi soglasno (4.64) zavisit tol'ko ot kombinacii μ₀M². Reshenie sistemy na sobstvennye znacheniya daet togda velichiny Π₁ i Π₂. Krome togo, v tablice privedeny otnositel'nye znacheniya radiusa (h_k) i massy (q_k) konvektivnogo yadra.

Tablica 3

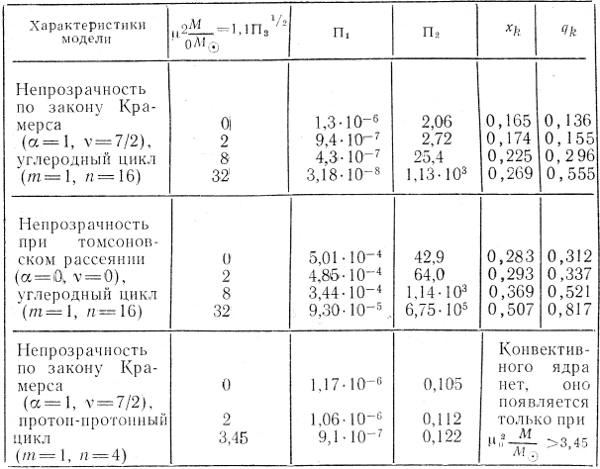
Iz etoi tablicy srazu sleduet, chto kompleks Π₁ uchityvayushii rol' koefficienta neprozrachnosti, otnositel'no slabo zavisit ot vybora Π₃, hotya i bolee sushestvenno zavisit ot vybora zakona neprozrachnosti. Kompleks Π₂ ochen' sil'no menyaetsya s izmeneniem roli luchevogo davleniya. Takzhe zametno menyayutsya razmery i massa konvektivnogo yadra.

V rabote [18] bylo rassmotreno eshe neskol'ko modelei. Naprimer, rassmatrivalis' zvezdy s uglerodnoi reakciei pri vysokih temperaturah, kogda n = 13, i zvezdy s gelievoi reakciei, gde m=2, n ≈ 30. Zdes' perenos energii svyazan s rasseyaniem na svobodnyh elektronah, t.e. α = 0, ν = 0. Okazalos', chto harakteristiki takih modelei malo otlichayutsya ot analogichnoi modeli v tabl. 3. V chastnosti, kompleksy Π₁ ostayutsya pochti takimi zhe po svoemu chislennomu znacheniyu. Malo izmenyayutsya i parametry konvektivnogo yadra. Tol'ko kompleks Π₂ okazalsya sushestvenno otlichnym. Dlya modelei s μ₀²M/M_☉ = 32 on raven 3,45 ⋅ 10⁴ v sluchae goryachei zvezdy s uglerodnym ciklom i 1,09 ⋅ 10⁷ - v sluchae modeli s gelievoi reakciei.

Analiz reshenii uravnenii etoi zadachi pri ξ ≠ 1 byl proveden V. I. Petruhinoi. Okazalos', chto i zdes' bezrazmernyi kompleks Π₁ pochti ne menyaetsya v intervale izmeneniya ξ ot 0,6 do 1,5. Dazhe kompleks Π₂ v etoi zadache menyaetsya vsego na neskol'ko procentov. Parametry konvektivnogo yadra takzhe pochti ne chuvstvuyut izmeneniya molekulyarnogo vesa.

Itak, rezyumiruya dannye analiza uravneniya stroeniya zvezd s tochki zreniya principa podobiya, mozhno utverzhdat' sleduyushee. V shirokom intervale vozmozhnyh znachenii shesti pokazatelei α, ν , n, m, ξ i η velichina bezrazmernogo kompleksa Π₁ mozhet schitat'sya pochti postoyannoi. Vse zvezdy podobny po bezrazmernomu kriteriyu (4.60).

S tochki zreniya fiziki zvezd etot rezul'tat eshe raz podcherkivaet universal'nost' sootnosheniya massa - svetimost', osnovannogo na bezrazmernom komplekse Π₁

Pravda, uchet luchevogo davleniya (t. e. kompleksa Π₃) vse zhe privodit k zametnym izmeneniyam kompleksa Π₁ Uchityvaya eti izmeneniya, V. S. Imshennik i D. K Nadezhin nahodyat, chto v oblasti bol'shih mass pri neprozrachnosti iz-za tomsonovskogo rasseyaniya vmesto (4.71) luchshe podhodit sootnoshenie

$\lg L = 2,5\lg M + const.$ (4.75)

Formula (4.67) (v kotoroi dlya togo, chtoby ubrat' postoyannuyu, luchshe vyrazit' svetimost' i massu v edinicah svetimosti i massy Solnca) horosho opisyvaet sootnoshenie massa - svetimost' pri vseh vozmozhnyh variantah, parametrov, no pri ne slishkom bol'shih massah.

Razumeetsya, vse skazannoe otnositsya tol'ko k teoreticheskomu vyvodu kriteriya podobiya, a otnyud' ne k rezul'tatam sravneniya teorii i nablyudenii. Nakonec, nuzhno otmetit' i to, chto hotya pri uchete luchevogo davleniya dlya kazhdoi konkretnoi massy zvezdy est' svoya model' - i v etom smysle zvezdy raznyh mass ne podobny drug drugu,- vse zhe stroenie ih priblizitel'no odinakovo i poetomu sushestvuet ogranichennoe podobie stroeniya zvezd raznyh mass s konvektivnymi yadrami v centrah.

Pri postroenii rassmotrennyh vyshe modelei ne uchityvalas' vozmozhnost' obrazovaniya konvektivnyh zon vblizi poverhnosti zvezdy. Poetomu takie modeli primenimy tol'ko dlya zvezd rannih spektral'nyh klassov, gde vodorod i gelii ionizovany do samoi poverhnosti i gde poetomu ne voznikayut poverhnostnye zony ionizacii. U zvezd pozdnih spektral'nyh klassov poverhnostnaya temperatura nizka, v okolopoverhnostnyh sloyah vodorod, a tem bolee gelii ne ionizovany, chto privodit k rezkomu uvelicheniyu neprozrachnosti. Krome togo, v zonah ionizacii vodoroda i geliya sushestvenno umen'shaetsya i pokazatel' adiabaty. Vse eto privodit k vozbuzhdeniyu konvekcii, i v pripoverhnostnyh sloyah zvezd pozdnih spektral'nyh klassov energiya perenositsya konvekciei. Zato zdes' ne obrazuetsya konvektivnyh yader. Poskol'ku spektral'nyi klass zvezdy svyazan s ee massoi, to otsyuda sleduet, chto u zvezd malyh mass est' konvektivnaya poverhnostnaya zona (kotoraya mozhet doiti i do centra u zvezd ochen' malyh mass), a u zvezd bol'shih mass est' konvektivnoe yadro (ris. 3).

Strogo govorya, obrazovanie konvektivnoi zony vblizi poverhnosti dolzhno sledovat' iz resheniya osnovnoi sistemy uravnenii, esli v nei uchest' vse izmeneniya koefficientov neprozrachnosti i pokazatelei adiabaty. No eto sdelat' trudno i poetomu luchshe uchest' obrazovanie poverhnostnyh konvektivnyh zon v granichnyh usloviyah.

Kak izvestno, v konvektivnoi zone imeet mesto politropnyi zakon r = K_γρ^γ Pokazatel' γ vblizi poverhnostnyh sloev zametno otlichen ot 5/3 (naprimer, v konvektivnoi zone Solnca vblizi fotosfery γ ≈ 1,16). No po mere pogruzheniya v glub' konvektivnoi zony velichina γ bystro priblizhaetsya k znacheniyu 5/3. Poetomu mozhno schitat', chto uzhe na nekotoroi nebol'shoi glubine (gde, skazhem, q ≈ 0,95-0,98) plotnost', temperatura ' davlenie veshestva svyazany usloviyami

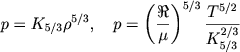
$p = K_{5/3}\rho^{5/3}, \quad p = \left(\frac{\Re}{\mu}\right)^{5/3}\frac{T^{5/2}}{K_{5/3}^{2/3}}$ (4.76)

Zdes' parametr K_5/3 dolzhen byt' opredelen iz teorii zvezdnyh atmosfer, uchityvayushei neadiabaticheskuyu konvekciyu. K sozhaleniyu, poka nadezhnyh opredelenii parametra K_5/3 Dlya etogo sluchaya net. Mozhno lish' poluchit' grubye ocenki.

Formula (4.76) v bezrazmernyh peremennyh (4.58) imeet vid

$p = \Pi_4 t^{\frac{5\eta}{5-3\xi}}$ (4.77)

gde novyi bezrazmernyi kompleks

$\Pi_4 = \left[4\pi\left(\frac{GM^{1/3}R}{K_{5/3}}\right)^{3/2}\right]^{\frac{2\xi}{5-3\xi}}.$ (4.78)

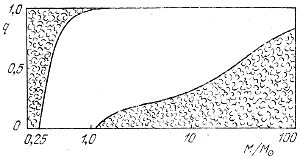
Ris. 3. Oblast' konvektivnyh zon i konvektivnyh yader u zvezd raznyh mass.

My ne uchli vozmozhnuyu zavisimost' parametra K_5/3 ot molekulyarnogo vesa, kotoryi v preobrazovanii (4.58) schitaetsya menyayushimsya. Vprochem, do sih por pri rassmotrenii modelei zvezd i poverhnostnymi konvektivnymi zonami ne uchityvalas' zavisimost' molekulyarnogo vesa ot plotnosti i temperatury, t. e. prinimalos' ξ = η. Pri etom (4.78) zapisyvaetsya v vide

$p = \Pi_4 t^{\frac{5}{2}}.$ (4.79)

gde bezrazmernyi kompleks Π₄, obychno oboznachaemyi cherez E, mozhno zapisat' cherez bezrazmernyi kompleks Π_5/3 konfiguracii, v kotoroi uravnenie sostoyaniya r ∼ ρ^5/3 imeet mesto po vsei masse:

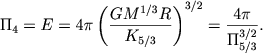
$\Pi_4 = E = 4\pi\left(\frac{GM^{1/3}R}{K_{5/3}}\right)^{3/2} = \frac{4\pi}{\Pi_{5/3}^{3/2}}.$ (4.80)

Otsyuda srazu sleduet, chto v polnost'yu konvektivnoi zvezde, gde Π_5/3 = 0,424, znachenie parametra E ravno 4π/(0,424)^3/2 = 45,5. Esli v (4.78) Π_5/3 < 45,5, to konvektivnaya zona zanimaet tol'ko chast' radiusa.

Teper' postanovka zadachi po postroeniyu modeli zvezdy s konvektivnoi zonoi zaklyuchaetsya v sleduyushem. Sistema uravnenii (4.59) (s uchetom (4.72) v zone konvekcii) i vyrazheniya (4.60) - (4.71) dlya bezrazmernyh kompleksov ostayutsya prezhnimi. V uslovii (4.62) luchevym davleniem mozhno prenebrech', poskol'ku v nizkotemperaturnyh zvezdah s poverhnostnoi konvektivnoi zonoi ono malo, t. e. mozhno prinyat' Π₃ = 0. Granichnoe uslovie v centre ostaetsya prezhnim (t. e. pri x = 0 imeem q = l = 0, r i t - konechny). Granichnoe uslovie na poverhnosti menyaetsya. Teper' sleduet schitat', chto pri x = 1

$q = 1, \quad l = 1, \quad \sigma = 0, p = Et^{5/2}.$ (4.81)

Zavisimost' r = Et^5/2 prodolzhaetsya v glub' do teh por, poka luchistyi gradient temperatury, opredelennyi v sisteme (4.59), ne stanet men'shim adiabaticheskogo gradienta (4.73).

I v etom sluchae velichiny Π₁ i Π₂ yavlyayutsya sobstvennymi znacheniyami sistemy uravnenii, no teper' oni zavisyat ot vybrannogo znacheniya bezrazmernogo kompleksa Π₄ = E. Podobnymi yavlyayutsya modeli s odinakovymi znacheniyami parametra E. Inymi slovami, podobnymi yavlyayutsya zvezdy, u kotoryh velichina K_5/3 = r/ρ^5/3 proporcional'na M^1/3R. K sozhaleniyu, kak uzhe otmechalos', trudno nadezhno opredelit' velichinu K_5/3 na osnovanii teorii zvezdnyh atmosfer.

Podobnye modeli zvezd s poverhnostnymi konvektivnymi zonami byli rasschitany Shvarcshil'dom i Osterbrokom (sm. izlozhenie v [1]) dlya sluchaya poglosheniya po zakonu Kramersa i proton-protonnogo cikla. Uchityvaya bol'shuyu plotnost' gaza i men'shuyu temperaturu v nedrah takih zvezd, byli prinyaty sleduyushie znacheniya pokazatelei: α = 0,75 i α = 0,50; ν = 7/2 v zakone poglosheniya i m = 1, n = 4,5 v sootnoshenii dlya moshnosti generacii energii. Rezul'taty opredeleniya bezrazmernyh kompleksov Π₁ i Π₂, a takzhe nizhnei granicy konvektivnoi zony x_k i doli massy v luchistom yadre privedeny v tabl. 4.

Tablica 4

Harakteristiki modeli	Π₄	Π₁	Π₂	x_k	q_k
Model' zvezdy tipa zheltogo karlika (α = 0,75, ν = 7/2, m=1, n = 4,5)	44,83	3,7 ⋅ 10^-6	7,8	0,413	0,310
	19,66	1,95 ⋅ 10^-6	1,19	0,698	0,914
	5,70	2,42 ⋅ 10^-6	0,198	0,801	0,991
	1,68	2,88 ⋅ 10^-6	0,074	0,871	0,999
Model' zvezdy tipa krasnogo karlika (α = 0,50, ν = 7/2, m=1, n = 4,5)	37,67	5,86 ⋅ 10^-6	4,92	0,558	0,636
	16,82	5,86 ⋅ 10^-6	0,074	0,676	0,913
	8,02	6,35 ⋅ 10^-6	0,0155	0,723	0,971

Kak i sledovalo ozhidat', umen'shenie bezrazmernogo kompleksa Π₄ umen'shaet massu i tolshinu konvektivnoi zony. Chislennye znacheniya bezrazmernyh kompleksov Π₁ i Π₂ togo zhe harakternogo poryadka, chto i u zvezd s konvektivnym yadrom, hotya oni, konechno, i zametno razlichayutsya.

U Solnca, prinadlezhashego k zvezdam tipa zheltogo karlika, velichina parametra E nevelika (nahoditsya, po-vidimomu, mezhdu edinicei i desyat'yu), poetomu konvektivnaya zona neglubokaya.

Ochen' protyazhennye konvektivnye zony imeyutsya u krasnyh gigantov. Zdes' velichina parametra E dostigaet obychno 25. Odnako slozhnaya struktura etih zvezd, sostoyashih iz chastichno vyrozhdennyh izotermicheskih yader, topkih sloevyh istochnikov energii, zon luchistogo i zon konvektivnogo perenosa, zatrudnyaet issledovaniya podobiya modelei etogo tipa zvezd. Obychno dlya rascheta takih modelei delayut kakie-libo predpolozheniya, ne pozvolyayushie opredelit' ih podobie v yavnom vide. Naprimer, v izvestnyh raschetah Shvarcshil'da (sm. [1]) vmesto nahozhdeniya bezrazmernogo kompleksa Π₂ prosto zadavalas' temperatura gaza v sloevom istochnike energii (T = 2 ⋅ 10^-7 gradusov). Sushestvennaya neopredelennost' svyazana i s opredeleniem radiusa zvezd s ochen' protyazhennymi konvektivnymi obolochkami.

Rol' konvekcii velika i u szhimayushihsya protozvezd. Pervonachal'no predpolagalos', chto v szhimayushihsya protozvezdah energiya perenositsya izlucheniem. Osnovaniem dlya takogo predpolozheniya byla sravnitel'no slabaya zavisimost' moshnosti vydeleniya energii ot temperatury i plotnosti pri gravitacionnom szhatii. V pervom priblizhenii pri gomologicheskom (odnorodnom) szhatii imeem

$\epsilon = \epsilon_0 T,$ (4.82)

t. e. m = 0 i n = 1. Takaya slabaya zavisimost' ε ot T umen'shaet gradient temperatury, a sledovatel'no, privodit k konvektivnoi ustoichivosti. Odnako veshestvo protozvezd pri nizkoi ionizacii i nalichii molekul, po-vidimomu, obladaet nizkoi prozrachnost'yu i poetomu mozhno ozhidat', chto zdes' energiya vse zhe perenositsya konvekciei. Soglasno predpolozheniyu Hayashi ([19]) prinyato schitat', chto v szhimayushihsya protozvezdah energiya v osnovnom perenositsya konvekciei i tol'ko na bolee pozdnih stadiyah szhatiya bolee massivnyh protozvezd v ih central'nyh chastyah obrazuyutsya luchistye yadra.

Uslovie podobiya dlya protozvezdy, v kotoroi energiya perenositsya tol'ko izlucheniem, netrudno poluchit' opisannym vyshe metodom s ispol'zovaniem formuly (4.82). V prenebrezhenii luchevym davleniem (Π₃ = 0) i konvektivnym perenosam v poverhnostnyh sloyah (Π₄ = 0) mozhno naiti znachenie bezrazmernyh kompleksov Π₁ i Π₂ (sm. [1]):

$\Pi_1 = 1,88 \cdot 10^{-6}, \quad \Pi_2 = 1,19.$ (4.83)

Tak zhe sravnitel'no prosto rasschityvayutsya metodom predydushego paragrafa polnost'yu konvektivnye szhimayushiesya protozvezdy. Zdes' Π₄ = E = 45,5. Velichina K_5/3 dolzhna byt' opredelena iz polnoi svetimosti protozvezdy i analiza uslovii na ee poverhnosti. Eto sdelat' ochen' slozhno, poskol'ku temperatura poverhnostei protozvezd nizka i vychislenie neprozrachnosti dovol'no neopredelenno. Szhimayushiesya modeli s konvektivnymi obolochkami i yadrami s luchistym perenosom energii byli rasschitany Hayashi i ego sotrudnikami (sm. [19] i stat'yu Hayashi v [10]).

<< § 4.3 Belye karliki i neitronnye zvezdy | Oglavlenie | § 4.5 Chislennoe modelirovanie evolyucii zvezd >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

$\lg R = \frac{(2+\alpha+m)\eta-(4+\nu-n)(2-\xi)}{(4+3\alpha+3m)\eta+(4+\nu-n)(3\xi - 4)} \lg M + const,$	(4.66)
$\lg L = \left[1+m+\frac{2-\xi}{\eta}n+\frac{[(2+\alpha + m)\eta - (4+\nu - n)(2-\xi)][(3\xi - 4)n - 3m\eta]}{\eta[(4+3\alpha + 3m)\eta + (4+\nu -n)(3\xi-4)]}\right]\lg M + const.$	(4.67)