po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 4.5 Chislennoe modelirovanie evolyucii zvezd | Oglavlenie | § 5.2 Vrashenie i magnitnye polya zvezd >>

Glava V. Stacionarnye dvizheniya v zvezdah

Obsheizvestno vyskazyvanie Eddigtona o tom, chto "net nichego proshe zvezdy". Odnako esli eto i spravedlivo, to tol'ko do teh por, poka my ne rassmatrivaem dvizheniya v zvezdah. Uchet vrasheniya i magnitnyh polei srazu vnosit sushestvennyi element neopredelennosti v teoriyu, poskol'ku raspredelenie skorostei vrasheniya i napryazhennosti magnitnyh polei vnutri zvezdy ostaetsya ne izvestnym. Neskol'ko luchshe obstoit delo s teoriei pul'sacii zvezd, gde mozhno schitat' ponyatnymi osnovnye cherty yavleniya. Pri issledovanii dvizhenii v zvezdah chasto trudno poluchit' bolee ili menee polnye uravneniya, kotorye mozhno bylo by reshit' odnoznachno. Zdes' soobrazheniya teorii razmernostei inogda ostayutsya edinstvenno vozmozhnymi.

V nastoyashei glave my rassmotrim s tochki zreniya teorii razmernostei i podobiya stacionarnye dvizheniya - pul'sacii zvezd, ih vrasheniya i magnitnye polya, a takzhe usloviya konvekcii i turbulentnosti v zvezdah, mezhzvezdnom prostranstve i atmosferah planet. V sleduyushei glave my rassmotrim nestacionarnye dvizheniya avtomodel'nogo tipa v zvezdah i mezhzvezdnom prostranstve.

§ 5.1 Pul'saciya peremennyh zvezd

Zvezdnye pul'sacii, t. e. periodicheskie szhatiya i rasshireniya zvezd s otnositel'no nebol'shoi amplitudoi, ochen' podrobno issledovalis' razlichnymi astrofizicheskimi metodami (sm. sbornik statei [1]). Ochen' mnogo rabot bylo posvyasheno i teoreticheskoi interpretacii etogo yavleniya. Mozhno otmetit' knigu Rosselanda [2], stat'i S. A. Zhevakina v sbornike [1] i ego obzor [3], a takzhe stat'i Bekkera, Koksa i Kristi v sbornike [4] i Kristi v sbornike [5].

V nastoyashee vremya teoreticheskii analiz yavleniya zvezdnoi peremennosti osnovan pochti isklyuchitel'no na chislennyh raschetah. No poskol'ku osnovnaya nasha cel' - nahozhdenie kriteriev podobiya v astrofizicheskih yavleniyah, to my rassmotrim zdes', hotya i priblizhenno, no zato s dostatochnoi obshnost'yu, analiticheskoe reshenie zadachi o vychislenii parametrov zvezdnyh pul'sacii.

Uravneniya struktury stacionarnyh zvezd, zapisannye v predydushei glave, ne uchityvayut dvizhenii gaza. Vnesem teper' v eti uravneniya chleny, opisyvayushie radial'nye pul'sacii zvezd. Obshaya teoriya uchityvaet i neradial'nye pul'sacii, odnako my eto delat' ne budem.

Uravneniya pul'sacii zvezd udobnee zapisyvat' v lagranzhevoi sisteme koordinat, rassmatrivaya v kachestve nezavisimoi peremennoi ne radius r, a massu, zaklyuchennuyu vnutri sfery radiusa r, t. e. velichinu, oboznachennuyu ran'she cherez M(r), a teper' oboznachaemuyu cherez M_r. V lagranzhevoi sisteme koordinat polozhenie dannogo elementa massy gaza est' r(M_r, t), t. e. yavlyaetsya funkciei massy vnutri sfery r i vremeni t kak nezavisimyh peremennyh. Iz usloviya nepreryvnosti sleduet pervoe uravnenie:

$\frac{\partial r}{\partial M_r} = \frac{1}{4\pi\rho r^2}.$ (5.1)

Uravnenie dvizheniya elementa massy pod deistviem kak gravitacionnoi sily, tak i gradienta davleniya, imeet vid

$\rho\frac{\partial^2 r}{\partial t^2} = -\frac{GM_r}{r^2}\rho - \frac{\partial p}{\partial r}$ (5.2)

ili, v lagranzhevyh peremennyh,

$\frac{\partial^2 r}{\partial t^2} = -\frac{GM_r}{r^2} - 4\pi r^2\frac{\partial p}{\partial M_r}.$ (5.3)

Uravnenie luchistoi teploprovodnosti v lagranzhevyh peremennyh zapishetsya v vide

$L_r = -\frac{64\pi^2 acr^4T^3}{3\varkappa}\frac{\partial T}{\partial M_r}.$ (5.4)

Zdes' L_r - kolichestvo energii, generiruemoe za sekundu vnutri sfery radiusa r, ili, inymi slovami, v oblasti, zanyatoi massoi M_r. Temperatura, kak i drugie parametry, zavisit ot M_r i t.

V uravnenii generacii energii teper' nuzhno uchest' i izmenenie teplovoi energii so vremenem pri pul'saciyah, a takzhe rabotu, sovershaemuyu pri szhatiyah i razrezheniyah. V lagranzhevyh koordinatah eto uravnenie imeet vid

$\frac{\partial L_r}{\partial M_r} = \epsilon - \left[\frac{\partial}{\partial t}(c_v T) - p\frac{\partial}{\partial t}\left(\frac{1}{\rho}\right) \right],$ (5.5)

gde ε - po-prezhnemu, moshnost' energii, vydelyaemoi v odnom gramme veshestva pri termoyadernyh reakciyah, c_vT - vnutrennyaya energiya edinicy massy gaza. Teploemkost' pri postoyannom ob'eme c_v mozhet byt' zapisana cherez harakternyi pokazatel' adiabaty dlya smesi gaza i izlucheniya Γ:

$c_v = \frac{1}{\Gamma - 1}\frac{\Re}{\mu},$ (5.6)

gde Γ est' funkciya β - otnosheniya gazovogo davleniya k polnomu:

$\beta = \frac{1}{1 + \frac{\mu aT^3}{3\Re\rho}}.$ (5.7)

S usloviem (5.6) uravnenie (5.5) prinimaet vid

$\frac{\partial L_r}{\partial M_r} = \epsilon + \frac{p}{\rho}\frac{\partial}{\partial t}\ln\left(\frac{\rho}{T^{\frac{1}{\Gamma - 1}}}\right).$ (5.8)

Zdes' pod ∂/∂ t - sleduet, voobshe govorya, ponimat' polnuyu proizvodnuyu po vremeni, t. e. s uchetom i chlena $v\frac{\partial}{\partial r}$ , gde v - skorost'.

Sistema uravnenii (5.1), (5.3), (5.4) i (5.8) sovmestno s opredeleniem funkcii ϰ , ε i μ , predstavlyaet soboi polnuyu sistemu uravnenii radial'nyh zvezdnyh pul'sacii. My primem dlya etih funkcii stepennye zavisimosti, vvedennye v predydushei glave.

Zdes' nuzhno sdelat' odno sushestvennoe zamechanie. V real'nyh pul'siruyushih zvezdah naibol'shie kolebaniya proishodyat vo vneshnih sloyah zvezd, v chastnosti, v zonah ionizacii vodoroda i geliya. Tam koefficient neprozrachnosti vedet sebya ochen' slozhnym obrazom, i lyubaya stepennaya zavisimost' okazyvaetsya nedostatochno tochnoi. Poetomu analiz, osnovannyi na stepennom predstavlenii koefficienta neprozrachnosti (chto neobhodimo dlya primeneniya metoda podobiya), mozhet rassmatrivat'sya lish' kak kachestvenno pravil'nyi. Bolee ili menee tochnaya kolichestvennaya teoriya zvezdnyh pul'sacii mozhet byt' postroena tol'ko na osnove chislennogo modelirovaniya s uchetom tablichnyh dannyh dlya koefficienta neprozrachnosti. Kratkoe opisanie chislennogo modelirovaniya pul'sacii my privedem nizhe.

Vozvratimsya k sisteme uravnenii, zapisannoi vyshe, i pereidem v nei k bezrazmernym peremennym, vvedennym v predydushei glave, a imenno:

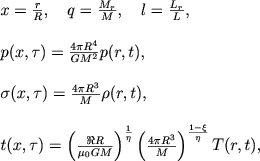
$\begin{array}{l} x = \frac{r}{R}, \quad q = \frac{M_r}{M}, \quad l = \frac{L_r}{L}, \\ \\ p(x, \tau) = \frac{4\pi R^4}{GM^2}p(r, t), \\ \\ \sigma(x, \tau) = \frac{4\pi R^3}{M}\rho(r, t), \\ \\ t(x, \tau) = \left(\frac{\Re R}{\mu_0 GM}\right)^{\frac{1}{\eta}} \left(\frac{4\pi R^3}{M}\right)^{\frac{1 - \xi}{\eta}}T(r, t), \end{array}$ (5.9)

gde t(h, τ) - bezrazmernaya temperatura. Krome togo, vvedem bezrazmernoe vremya po formule

$\tau = t\sqrt{\frac{GM}{R^3}},$ (5.10)

gde t - razmernoe vremya. Sistema uravnenii pul'sacii v bezrazmernom vide zapishetsya tak (teper' q i τ est' nezavisimye peremennye):

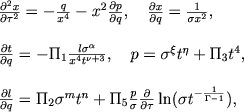
$\begin{array}{l} \frac{\partial^2 x}{\partial \tau^2} = - \frac{q}{x^4} - x^2\frac{\partial p}{\partial q}, \quad \frac{\partial x}{\partial q} = \frac{1}{\sigma x^2}, \\ \\ \frac{\partial t}{\partial q} = -\Pi_1\frac{l\sigma^\alpha}{x^4t^{\nu+3}}, \quad p = \sigma^\xi t^\eta + \Pi_3 t^4, \\ \\ \frac{\partial l}{\partial q} = \Pi_2 \sigma^m t^n + \Pi_5\frac{p}{\sigma} \frac{\partial}{\partial \tau}\ln(\sigma t^{-\frac{1}{\Gamma - 1}}), \end{array}$ (5.11)

gde Π₁, Π₂, Π₃ - bezrazmernye kompleksy, opredelennye v predydushei glave:

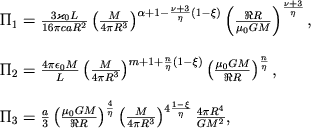
$\begin{array}{l} \Pi_1 = \frac{3\varkappa_0 L}{16\pi caR^2}\left(\frac{M}{4\pi R^3}\right)^{\alpha + 1 - \frac{\nu+3}{\eta}(1-\xi)} \left(\frac{\Re R}{\mu_0 GM}\right)^{\frac{\nu+3}{\eta}},\\ \\ \Pi_2 = \frac{4\pi\epsilon_0 M}{L}\left(\frac{M}{4\pi R^3}\right)^{m + 1 + \frac{n}{\eta}(1-\xi)} \left(\frac{\mu_0 GM}{\Re R}\right)^{\frac{n}{\eta}},\\ \\ \Pi_3 = \frac{a}{3}\left(\frac{\mu_0 GM}{\Re R}\right)^{\frac{4}{\eta}}\left(\frac{M}{4\pi R^3}\right)^{4\frac{1-\xi}{\eta}} \frac{4\pi R^4}{GM^2}, \end{array}$ (5.12)

a Π₅ est' novyi bezrazmernyi kompleks:

$\Pi_5 = \frac{1}{GL}\left(\frac{GM}{R}\right)^{5/2}.$ (5.13)

Pul'sacii zvezd, kak pravilo, maly po amplitude. Naibol'shaya velichina amplitudy pul'sacii, dostigaemaya u poverhnosti zvezdy, redko prevyshaet 5%. V glubokih sloyah zvezdy amplituda pul'sacii poryadka 10^-3. Hotya pul'sacii ne vsegda mozhno schitat' lineinymi, no v pervom priblizhenii my ogranichimsya lineinoi zadachei. Poputno otmetim, chto chastnyi sluchai nelineinyh, no adiabaticheskih pul'sacii gazovogo shara, dopuskayushii analiticheskoe reshenie, byl ukazan L. I. Sedovym.

Linearizuem sistemu uravnenii (5.11). Dlya etogo proizvedem zamenu iskomyh funkcii p → p(1+p'), x → x(1+x')... i t. d., gde shtrihovannye velichiny est' bezrazmernye funkcii argumentov q i τ, a neshtrihovannye zavisyat tol'ko ot q i opisyvayut stacionarnoe ravnovesnoe sostoyanie. Budem schitat', chto vse shtrihovannye velichiny mnogo men'she edinicy. V nulevom priblizhenii neshtrihovannye velichiny udovletvoryayut uravneniyam ravnovesiya, a v sleduyushem, pervom priblizhenii poluchaem lineinye uravneniya dlya shtrihovannyh velichin:

$\begin{array}{l} \frac{\partial p'}{\partial q} + \frac{1}{xp}\frac{\partial^2 p'}{\partial \tau^2} = \frac{q}{x^4p}(p' + 4x'), \\ \\ \frac{\partial x'}{\partial q} = -\frac{\sigma' + 3x'}{x^3\sigma}, \\ \\ \frac{\partial t'}{\partial q} = -\Pi_1 \frac{l\sigma^{\alpha}}{x^4t^{\nu+4}}[l' + \alpha\sigma' - (\nu + 4)t' - 4x'], \\ \\ \frac{\partial l'}{\partial q} = \Pi_2 \frac{\sigma^mt^n}{l}(m\sigma' + nt' - t) + \Pi_5\frac{p}{\sigma l}\left(\frac{\partial \sigma'}{\partial \tau} - \frac{1}{\Gamma - 1}\frac{\partial t'}{\partial \tau}\right), \\ \\ p' = \frac{\sigma^\xi t^\eta}{p}(\xi\sigma' + \eta t') + 4\Pi_3\frac{t^4}{p}t'. \end{array}$ (5.14)

V etoi sisteme uravnenii neshtrihovannye velichiny opredelyayutsya sistemoi uravnenii (4.59), kotoruyu mozhno perepisat' v koordinatah Lagranzha:

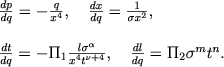
$\begin{array}{l} \frac{dp}{dq} = -\frac{q}{x^4}, \quad \frac{dx}{dq} = \frac{1}{\sigma x^2}, \\ \\ \frac{dt}{dq} = -\Pi_1 \frac{l\sigma^{\alpha}}{x^4t^{\nu+4}}, \quad \frac{dl}{dq} = \Pi_2 \sigma^m t^n . \end{array}$ (5.15)

Reshenie etoi sistemy my budem schitat' izvestnym.

Ochevidno, chto sistema (5.14) opisyvaet pul'sacii (est' vtoraya proizvodnaya $\frac{\partial^2 x}{\partial \tau^2}$ No nalichie proizvodnyh po q oznachaet, chto imeet mesto svoeobraznaya dispersiya. Pri issledovanii pul'sacii v plazme analogichnoe yavlenie nazyvaetsya prostranstvennoi dispersiei. Zdes' etu osobennost' sistemy mozhno nazvat' dispersiei po lagranzhevoi koordinate.

Primenim teper' k sisteme (5.14) obychnye metody teorii malyh kolebanii. Vospol'zuemsya priblizheniem, ekvivalentnym metodu Ventcelya - Kramersa - Brillyuena, t. e. budem schitat', chto proizvodnye po q shtrihovannyh velichin mnogo bol'she, chem proizvodnye po q ne shtrihovannyh velichin.

Togda reshenie sistemy (5.14) mozhno iskat' v vide

$p',x',t',l' \sim e^{i(\omega\tau-Kq)},$ (5.16)

gde ω - bezrazmernaya chastota (vyrazhennaya v edinicah vremeni t soglasno (5.10)), a K - analog volnovogo chisla.

Podstavlyaya (5.16) v (5.14), poduchim sistemu:

$\begin{array}{l} -iKp' - \frac{\omega^2 x'}{xp} - \frac{q}{x^4p}(p' + 4x') = 0, \\ \\ -iKx^3\sigma x' + 3x' + \sigma' = 0, \\ \\ -iKx^4t^{\nu+4}t' + \Pi_1l\sigma^2[l' + \alpha\sigma' - (\nu + 4)t' - 4x'] = 0, \\ \\ -iKl' - \Pi_2 \frac{\sigma^mt^n}{l}(m\sigma' + nt' - t') + \Pi_5\frac{p}{\sigma l}i\omega\left(\sigma' - \frac{1}{\Gamma - 1}t'\right) = 0, \\ \\ p' - \frac{\sigma^\xi t^\eta}{p}(\xi\sigma' + \eta t') + 4\Pi_3\frac{t^4}{p}t' = 0. \end{array}$ (5.17)

Eto i est' sistema odnorodnyh uravnenii (no s peremennymi koefficientami). Isklyuchaya otsyuda vse shtrihovannye velichiny, mozhno poluchit' dispersionnoe sootnoshenie, opredelyayushee zavisimost' ω(K). V obshem vide dispersionnoe sootnoshenie poluchaetsya gromozdkim, poetomu ne budem ego vypisyvat'. Sushestvenno legche ponyat' vsyu kartinu, esli snachala maksimal'nym obrazom uprostit' sistemu (5.17), a potom posledovatel'no uchityvat' vse bolee slozhnye sluchai.

Naibolee prostoi sluchai - pul'sacii bez dispersii po lagranzhevoi koordinate, t. e. pri K = 0. Etot sluchai nazyvaetsya model'yu odnoi zony (sm. stat'yu Bekkera v [4]). V samom dele, zdes' kolebaniya kazhdogo sloya v zvezde proishodyat nezavisimo ot drugih sloev, hotya parametry pul'sacii raznyh sloev razlichny. Uprostim zadachu eshe dal'she. Poskol'ku pul'sacii obychno imeyut mesto v sloyah zvezdy vblizi ee poverhnosti, prenebrezhem rol'yu luchevogo davleniya (Π₃ = 0) i termoyadernymi reakciyami (Π₂ = 0). Togda dispersionnoe sootnoshenie okazyvaetsya sovsem prostym, iz nego vypadaet dazhe kompleks Π₅.

Pul'sacii v etom sluchae imeyut adiabaticheskii harakter (t' = (Γ - 1)σ') i chastota etih pul'sacii opredelyaetsya kubicheskim uravneniem

$\omega(\omega^2 - B\omega_q^2) = 0$ (5.18)

gde vvedeny novye oboznacheniya:

$\omega_q = \sqrt{\frac{q}{x^3}}, \quad B = 3(\Gamma - 1)\eta + 3\xi - 4.$ (5.19)

Iz uravneniya (5.18) sleduet sushestvovanie treh reshenii:

$\omega_{2,1} = \pm\omega_q\sqrt B, \quad \omega_3 = 0.$ (5.20)

Esli ot bezrazmernoi chastoty so pereiti k razmernym chastotam i periodam, to poluchim sleduyushee vyrazhenie dlya perioda kolebanii sloya na rasstoyanii s ot centra zvezdy:

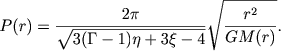
$P(r) = \frac{2\pi}{\sqrt{3(\Gamma - 1)\eta + 3\xi - 4}}\sqrt{\frac{r^2}{GM(r)}}.$ (5.21)

Pri η = ξ = 1 chislennyi mnozhitel' okazyvaetsya ravnym $2\pi/\sqrt{3\Gamma - 4}$ . Itak, pul'sacii sloya vozmozhny, esli B < 0 (ekvivalentno usloviyu Γ < 4/3 pri η = ξ = 1) i period kolebanii, kak i sledovalo ozhidat', obratno proporcionalen kornyu iz srednei plotnosti chasti zvezdy, ogranichennoi pul'siruyushim sloem. Eto i est' samyi prostoi sluchai. Budem teper' uslozhnyat' model'. Popytaemsya snachala uchest' vozmozhnuyu neadiabatichnost' kolebanii. Inymi slovami, dopustim, chto mezhdu raznymi pul'siruyushimi sloyami proishodit obmen energiei. No, po-prezhnemu, budem prenebregat' luchevym davleniem (Π₃ = 0) i termoyadernymi reakciyami (Π₂ = 0).

Pri neadiabaticheskih pul'saciyah $\sigma' \ne \frac{1}{\Gamma - 1}t'$ . Poetomu v chetvertom uravnenii sleduet sohranit' chlen iKl'. Eto i ochevidno, poskol'ku teper' iz-za obmena energiei poyavlyaetsya i dispersiya po lagranzhevoi koordinate. Esli sohranit' chleny s iK vo vseh uravneniyah sistemy (5.17), to dispersionnoe uravnenie opyat' okazhetsya gromozdkim.

No mozhno vospol'zovat'sya sleduyushimi rassuzhdeniyami. Dopustim, chto chastota pul'sacii kazhdogo sloya zvezdy opredelyaetsya tol'ko parametrami, sootvetstvuyushimi polozheniyu sloya vnutri zvezdy, a vzaimodeistvie mezhdu sloyami svoditsya lish' k poyavleniyu neadiabatich-nosti. Togda v uravneniyah (5.17) mozhno sohranit' lish' chlen iKl', a vse ostal'nye chleny s iK opustit'. V etom sluchae dispersionnoe uravnenie opyat' okazyvaetsya sravnitel'no prostym:

$\omega(\omega^2 - B\omega_q^2) + i\frac{K\sigma l}{p\Pi_5}(A\omega^2 - C\omega_q^2) = 0,$ (5.22)

gde novye koefficienty A i S sut':

$\begin{array}{l} A = (\Gamma - 1)(\nu +4), \\ C = (\Gamma - 1)[(3\alpha + 4)\eta + (\nu +4)(3\xi - 4)]. \end{array}$ (5.23)

Uravnenie (5.22) dlya sluchaya η = ξ = 1 bylo polucheno iz drugih soobrazhenii Bekkerom (sm. [4]).

Srazu iz (5.22) sleduet, chto uchet neadiabatichnosti privodit k poyavleniyu mnimyh chlenov v chastotah pul'sacii, t. e. k zatuhaniyu ili raskachke etih kolebanii. Uravnenie (5.22) mozhno legko reshit' dlya sluchaya, kogda mnozhitel' $\frac{K\sigma l}{p\Pi_5}$ mal. Vospol'zuemsya etim priblizheniem. Budem iskat' reshenie v vide

$\omega_{1,2} = \omega_q\sqrt B\left(\pm 1 + \frac{i}{s}\right),$ (5.24)

gde s ≫ l. Esli podstavit' (5.24) v (5.16), to poluchim

$p',x',l',t' \sim e^{i(\omega_q\sqrt{B}t - Kq)}e^{-\frac{\omega_q\sqrt{B}}{s}t}.$

Otsyuda sleduet, chto v sluchae s > l pul'sacii zatuhayut, prichem s est' chislo kolebanii pered tem, kak ih amplituda umen'shitsya v 2,7 raza. Velichina s nazyvaetsya dobrotnost'yu. Esli s < l, to kolebaniya raskachivayutsya i sistema okazyvaetsya neustoichivoi.

Podstavim (5.24) v (5.22), sohraniv tol'ko chleny pervogo poryadka po 1/s i schitaya, chto 1/s i $\frac{K\sigma l}{p\Pi_5}$ odnogo poryadka malosti. Togda poluchim

$s = \Pi_5\frac{2p}{\sigma lK}\frac{B^{3/2}}{AB - C}.$ (5.25)

Pereidem k razmernym velichinam, uchityvaya takzhe opredeleniya (5.21) i (5.23). Poluchim

$s = \frac{4\pi[3(\Gamma - 1)\eta + 3\xi - 4]^{\frac{3}{2}}}{(\Gamma - 1)\eta[3(\Gamma - 1)(\nu + 4) - 3\alpha - 4]} \frac{U_k(r)}{P(r)L(r)},$ (5.26)

gde

$U_k(r) = \frac{M\Re T(r)}{K\mu}.$ (5.27)

Bezrazmernoe volnovoe chislo K soglasno (5.16) est' harakteristika massy sloya s zametnym obmenom energiei. Mozhno priblizhenno schitat', chto K ≈ M/ΔM, gde ΔM - massa etogo sloya. V takom sluchae U_k(r) est', s tochnost'yu do chislennogo mnozhitelya, velichina teplovoi energii etogo sloya. Proizvedenie P(r)L(r) est' kolichestvo energii, prohodyashei cherez etot sloi za odin period pul'sacii. Ochevidno, chto velichina U_k(r)/P(r)L(r) mnogo bol'she edinicy. Zametim, chto s s tochnost'yu do chislennogo mnozhitelya sootvetstvuet obratnoi velichine kompleksa Π₂ v (1.21). Znak velichiny s opredelyaetsya znakom znamenatelya, poskol'ku pri pul'saciyah znak chislitelya vsegda polozhitelen. Pul'sacii zatuhayut, esli

$3(\Gamma - 1)(\nu + 4) - 3\alpha - 4 > 0,$ (5.28)

i raskachivayutsya v protivopolozhnom sluchae. Uslovie (5.28) nazyvaetsya usloviem kolebatel'noi ustoichivosti. Perepishem ego v neskol'ko drugom vide:

$4(\Gamma - 1) - [\alpha - (\Gamma - 1)\nu] - \frac{4}{3} > 0,$

Kazhdyi iz chlenov etogo sootnosheniya imeet opredelennyi fizicheskii smysl. Pervyi chlen 4(G - 1) opredelyaet poteryu mehanicheskoi energii pri szhatii i razrezhenii gaza - eta poterya vsegda privodit k zatuhaniyu kolebanii. V zone sushestvennoi ionizacii velichina G-1 mala i poetomu poterya mehanicheskoi energii nevelika. Tretii chlen 4/3 opisyvaet effekt sfericheskoi geometrii. V ploskom pul'siruyushem sloe velichinu 4/3 sleduet opustit'.

Osnovnym yavlyaetsya vtoroi chlen, kotoryi uchityvaet izmenenie neprozrachnosti za period pul'sacii. Uvelichenie plotnosti i temperatury pri szhatii mozhet i uvelichit' i umen'shit' neprozrachnost' v zavisimosti ot sootnosheniya mezhdu α i ν . Esli α - (G - 1)ν < 0 (kak eto imeet mesto, naprimer, v zakone Kramersa pri ne slishkom malyh G-1), to pogloshenie pri szhatii preobladaet nad pereizlucheniem pri rasshirenii i poetomu zdes' tozhe imeet mesto zatuhanie pul'sacii. Odnako v zonah ionizacii G-1 malo i, krome togo, pokazatel' ν pri nizkih temperaturah menyaet znak, tak chto velichina α - (G - 1)ν < 0 mozhet okazat'sya polozhitel'noi i dostatochno bol'shoi i vmesto zatuhaniya kolebanii poyavlyaetsya raskachka. Imenno takim putem podderzhivayutsya nezatuhayushie pul'sacii, kogda zatuhanie kolebaniya v odnih sloyah pri vypolnenii usloviya (5.28) kompensiruetsya "otricatel'noi dissipaciei" v drugih sloyah s obratnym znakom neravenstva (5.28). Kak pokazal S. A. Zhevakin eshe v 1953 g., zona vtorichnoi ionizacii geliya sluzhit istochnikom podderzhaniya pul'sacii peremennyh zvezd. Posleduyushie raschety (sm. nizhe) pokazali, chto i v zonah ionizacii vodoroda imeet mesto "otricatel'naya dissipaciya". K voprosu ob usloviyah podderzhaniya pul'sacii my vernemsya nizhe.

Tret'e reshenie uravneniya (5.23), sootvetstvuyushee resheniyu ω = 0 v uravnenii (5.18), mozhno iskat' srazu, polagaya ω v (5.22) maloi velichinoi (t. e. prenebregaya chlenami s ω²). Togda poluchim

$\omega_3 = -i\frac{\sigma l }{p\Pi_5} K\frac{C}{B}.$ (5.29)

Otsyuda nahodim uslovie tak nazyvaemoi vekovoi, ili sekulyarnoi, ustoichivosti zvezdy:

$\frac{C}{B} = \frac{(\Gamma - 1)[(3\alpha + 4)\eta + (\nu +4)(3\xi - 4)]}{3(\Gamma - 1)\eta + 3\xi - 4} < 0.$ (5.30)

Otsyuda, kstati, sleduet, chto v sluchae ξ < 1 i η < 1 zvezda stanovitsya bolee ustoichivoi, chem pri η = 1 i ξ = 1.

Vernemsya k obshei sisteme (5.17) i rassmotrim ee v drugom priblizhenii. Kak uzhe otmechalos', neadiabatichnost' kolebanii trebuet, chtoby t' ≠ (Γ - 1)σ'. Vyshe dlya ucheta neadiabatichnosti sohranyalsya chlen s iK. Ego mozhno opustit', no zato sohranit' chleny s Π₂. Poetomu rassmotrim sistemu (5.17) pri sleduyushih usloviyah. Polozhim K = 0, no sohranim chleny s Π₂, Π₅ i Π₃. Eto oznachaet, chto teper' my uchityvaem vozmozhnost' vydeleniya termoyadernoi energii v pul'siruyushem sloe, a takzhe uchityvaem vliyanie luchevogo davleniya. No zato opyat' ne uchityvaetsya vzaimodeistvie mezhdu pul'siruyushimi sloyami (odnosloinaya model').

V takoi postanovke sistema (5.17) mozhet opisyvat', naprimer, pul'sacii v sloevyh istochnikah goreniya vodoroda ili geliya, kotorye rassmatrivalis' v predydushei glave. No primenimost' etogo sluchaya dazhe shire. Ved' formula ε = ε₀ρ^mTⁿ mozhet opisyvat' ne tol'ko termoyadernye reakcii. Vsegda, kogda v veshestve est' neobratimoe vydelenie ili pogloshenie energii po kakomu-libo zakonu, mozhno ispol'zovat' etu formulu s sootvetstvuyushim podborom koefficientov e0, tip. V sluchae neobratimogo poglosheniya energii ε₀ < 0. Uslovie "neobratimosti" vydeleniya ili poglosheniya energii oznachaet, chto rassmatrivayutsya mehanizmy, vsegda deistvuyushie tol'ko v odnom napravlenii.

Uchet luchevogo davleniya (sohranenie parametra Π₃) provedem, ispol'zuya oboznachenie β - otnoshenie gazovogo davleniya k polnomu. Poskol'ku metod polucheniya dispersionnogo uravneniya dlya etogo sluchaya nichem ne otlichaetsya ot rassmotrennogo ranee, to my ogranichimsya lish' zapis'yu okonchatel'nyh formul. Iz tret'ego uravneniya (5.17) vidno, chto dispersionnoe sootnoshenie pri K=0 budet zaviset' ot otnosheniya Π₂/Π₅, a ne ot kazhdogo iz etih kompleksov po otdel'nosti. Poetomu udobnee rassmotret' predel'nye sluchai, kogda velichina

$Q = \frac{\Pi_2}{\Pi_5} = \frac{4\pi\epsilon_0 R^{5/2}}{(GM)^{3/2}}\left(\frac{M}{4\pi R^3}\right)^{m+1+\frac{n}{\eta}(1-\eta)}\left(\frac{\mu_0}{\Re}\frac{GM}{R}\right)^{\frac{n}{\eta}}$ (5.31)

mnogo bol'she libo mnogo men'she edinicy.

Kak i ran'she, isklyuchaya iz (5.17) vse shtrihovannye velichiny, poluchim dispersionnoe uravnenie, iz kotorogo, esli prenebrech' chlenom libo proporcional'nym Q, libo proporcional'nym 1/Q (v zavisimosti ot velichiny etogo kompleksa), sleduet tri resheniya. Odno iz nih vsegda sootvetstvuet nulevoi chastote, a dva drugih, razlichayushihsya tol'ko znakom (kak i v sluchae (5.20)), sootvetstvuet kolebaniyam s periodami

Vyrazhenie (5.32) perehodit v (5.21) pri β = 1. Eto i ochevidno, ibo uslovie Q ≪ 1 oznachaet, chto neobratimoe vydelenie energii otnositel'no malo. V sluchae, kogda moshnost' vydeleniya energii velika (t. e. Q ≫ 1),periody pul'sacii menyayutsya, no tol'ko za schet chislennogo mnozhitelya. Sravnivaya (5.32) i (5.33), ubezhdaemsya, chto oni perehodyat drug v druga, esli v (5.33) vvesti effektivnyi politropnyi pokazatel'

$P(r) = \frac{2\pi}{\sqrt{(\Gamma - 1)[\beta\eta + 4(1-\beta)] + 3\beta\xi - 4}}\sqrt{\frac{r^3}{GM(r)}},$ (5.32)

$P(r) = \frac{2\pi}{\sqrt{\frac{3\alpha + 4 + 3m}{\nu + 4 - n}[\beta\eta + 4(1-\beta)] + 3\beta\xi - 4}}\sqrt{\frac{r^3}{GM(r)}},$ (5.33)

Iz (5.33) takzhe .sleduet, chto pul'sacii vozmozhny, esli pokazatel' ne slishkom bol'shoi, inache podkorennoe vyrazhenie ili effektivnyi politropnyi indeks stanut otricatel'nymi.

Sleduyushee priblizhenie, t. e. sohranenie chlenov s Q ili 1/Q, pozvolit opredelit' uslovie raskachki ili zatuhanie pul'sacii. Ne budem privodit' zdes' formuly, analogichnye (5.26), no vypishem srazu kriterii zatuhaniya pul'sacii:

$3(\Gamma - 1)(\nu + 4 - n) - 3\alpha - 4 - 3m > 0.$ (5.34)

Eta formula spravedliva kak pri Q ≪ 1, tak i pri Q ≫ 1. Neravenstvo (5.34) perehodit v (5.28) pri n = m = 0, kak eto i sledovalo ozhidat'. Takzhe ochevidno, chto uchet neobratimogo vydeleniya energii vsegda oblegchaet raskachku pul'sacii - v kriterii (5.34) oba pokazatelya n i m vhodyat so znakom minus. Lyubopytno, chto kriterii raskachki ne zavisit ot roli luchevogo davleniya.

Kriterii vekovoi, ili sekulyarnoi, ustoichivosti v sluchae Q ≪ 1 imeet vid

$\frac{(3\alpha + 4 + 3m)[\beta\eta + 4(1-\beta)] + (\nu + 4 - n)(3\beta\xi - 4)}{3(\Gamma - 1)[\beta\eta + 4(1-\beta)] + 3\beta\xi - 4} < 0$ (5.35)

Eto uslovie obobshaet (5.30) na sluchai ucheta neobratimogo vydeleniya energii i luchevogo davleniya.

Rassmotrenie raznyh modelei pul'sacii mozhno bylo by prodolzhit', no my vernemsya k pervomu prostomu sluchayu, ibo imenno etot sluchai opisyvaet, konechno v grubom priblizhenii, real'nye pul'sacii peremennyh zvezd, gde vsegda pul'siruyut sloi, raspolozhennye vblizi poverhnosti.

Formula (5.21) opredelyaet period pul'sacii nekotorogo sloya, a formula (5.26) harakterizuet raskachku ili zatuhanie kolebanii v etom sloe (opredelennom zadannoi velichinoi K) - Soglasno metodu polucheniya resheniya bylo prinyato, chto v pul'siruyushem sloe vse parametry (t. e. nevozmushennye plotnost', temperatura, koefficienty α, ν, η, m i t. p.) postoyanny libo menyayutsya medlenno.

V real'noi pul'siruyushei zvezde polozhenie, konechno, sushestvenno slozhnee. Vo-pervyh, pul'siruet ne odin sloi, v kotorom parametry ne menyayutsya po tolshine, a dovol'no shirokaya zona, na protyazhenii kotoroi i nevozmushennye parametry i menyayushiesya so vremenem velichiny var'iruyutsya na poryadki. Bolee togo, i eto osnovnoe dlya ob'yasneniya pul'sacii, v odnoi chasti vsei etoi zony imeet mesto polozhitel'naya dissipaciya energii (vypolneno neravenstvo (5.28)), kotoraya dolzhna obyazatel'no kompensirovat'sya otricatel'noi dissipaciei v drugoi chasti zony, inache pul'sacii budut bystro zatuhat'. Inymi slovami, v pul'siruyushih zvezdah parametr s dolzhen menyat' znak na protyazhenii vsei pul'siruyushei zony. Uchet etogo effekta mozhno provesti, razbiv vsyu zonu na otdel'nye sloi, v predelah kotoryh mozhno schitat' postoyannymi otdel'nye parametry, i reshat' sistemu svyazannyh uravnenii, opisyvayushih kolebaniya vseh sloev.

Vo-vtoryh, v real'noi pul'siruyushei zvezde sushestvenny i nelineinye effekty. Szhatie i razrezhenie gaza pri pul'saciyah izmenyayut kak usloviya perenosa izlucheniya (poskol'ku, kak my videli, koefficient neprozrachnosti ochen' chuvstvitelen k variaciyam temperatury), tak i stepen' ionizacii: v zonah, gde proishodit ionizaciya vodoroda i geliya, dazhe nebol'shie izmeneniya temperatury privodyat k sushestvennomu izmeneniyu sostoyaniya ionizacii. Eto oznachaet, chto dazhe pri otnositel'no nebol'shih pul'saciyah neravenstva (5.28), kotorye mogut byt' vypolneny, naprimer, v moment naibol'shego szhatiya, mogut prevratit'sya v obratnye neravenstva v moment naibol'shego rasshireniya, ili naoborot. Inymi slovami, raskachka pul'sacii osnovana na takom tonkom balanse vseh velichin, chto pri ne ochen' bol'shih amplitudah parametr s nachinaet menyat' znak uzhe v techenie odnogo perioda. Sledovatel'no, pri bol'shih amplitudah raskachka pul'sacii prekrashaetsya.

Vozmozhny i drugie nelineinye effekty - obrazovanie udarnyh voln, vzaimodeistvie radial'nyh i neradial'nyh pul'sacii i t. d.

V-tret'ih, stepennoe predstavlenie koefficienta neprozrachnosti v vide ϰ = ϰ₀ρ^α/T^ν yavlyaetsya ochen' grubym priblizheniem, osobenno v oblasti ionizacionnyh zon, gde koefficient neprozrachnosti velik i menyaetsya s temperaturoi ochen' sushestvenno. Poetomu dlya analiza pul'sacii real'nyh zvezd prihoditsya pol'zovat'sya tablicami koefficienta neprozrachnosti.

V-chetvertyh, v zonah ionizacii bol'shuyu rol' igraet konvektivnyi perenos energii. Raskachka kolebanii svyazana s reakciei koefficienta neprozrachnosti na izmeneniya temperatury i plotnosti pri pul'saciyah i poetomu pri zamene luchistogo perenosa energii na konvektivnyi perenos ves' effekt voobshe ischezaet.

Vse skazannoe vyshe oznachaet, chto bolee ili menee adekvatnyi analiz yavleniya pul'sacii zvezd mozhno provesti lish' v ramkah chislennogo modelirovaniya vsego yavleniya putem chislennogo zhe resheniya osnovnoi sistemy uravnenii (5.1), (5.3), (5.4), (5.8) s ispol'zovaniem tablichnyh dannyh dlya koefficienta neprozrachnosti ϰ. Zdes' trudno naiti usloviya podobiya modelei pul'siruyushih zvezd, poskol'ku prihoditsya rasschityvat' otdel'nuyu model' dlya kazhdoi zvezdy s konkretno zadannymi parametrami (massa, svetimost', poverhnostnaya temperatura).

Takie raschety dlya razlichnyh zvezd provodilis' neodnokratno. S metodikoi rascheta mozhno poznakomit'sya po stat'yam Koksa i Kristi v [4, 5] i po rabote V.I.Aleshina [6]. Metod rascheta zaklyuchaetsya v sleduyushem. Snachala rasschityvaetsya model' stacionarnoi ravnovesnoi zvezdy. Zatem ei zadaetsya nekotoroe vozmushenie i proslezhivayutsya pul'sacii zvezdy na mnogo kolebanii do teh por, poka ustanavlivaetsya opredelennyi period i amplituda pul'sacii. Pri reshenii prihoditsya razbivat' zony ionizacii na bol'shoe chislo sloev.

Poskol'ku vnutrennyaya chast' zvezdy, v chastnosti, oblast', gde protekayut termoyadernye reakcii, pochti ne uchastvuet v pul'sacii (zdes' net raskachki, t. e. neravenstva (5.28) vsegda vypolneny), to mozhno schitat', chto na vnutrennei granice pul'siruyushei zony vse parametry i, v chastnosti, potok energii L_r, ostayutsya vse vremya postoyannymi. Ocenki pokazyvayut, chto amplituda kolebanii zdes' menee 10^-3 ot amplitudy pul'sacii na poverhnosti [5]. Na vneshnei granice davlenie i plotnost' obrashayutsya v nul', no pri etom temperatura gaza priravnivaetsya k effektivnoi temperature zvezdy.

Rezul'taty raschetov mozhno predstavit' v vide tablic i grafikov, illyustriruyushih izmenenie raznyh parametrov kak na poverhnosti zvezdy, tak i v glubokih sloyah. V kachestve primera privedem nekotorye rezul'taty rascheta Kristi [7, 8].

Vybrana model' zvezdy s parametrami M=0,4M_☉, L = 1,5 ⋅ 10³⁵ erg ⋅ sek^-1, T_eff = 6500°; K. Vneshnie sloi zvezdy razbivalis' na sorok sloev (numeraciya iz glubiny k poverhnosti) i proslezhivalos' dvizhenie kazhdogo sloya. Bylo zadano nekotoroe nachal'noe sinusoidal'noe vozmushenie v glubine i proschityvalas' dal'neishaya evolyuciya sistemy. Stacionarnoe znachenie perioda, ravnoe 5,7 ⋅ 10⁴ sek, ustanavlivaetsya ochen' bystro, vsego cherez neskol'ko kolebanii. Nachal'naya amplituda izmeneniya radiusa zvezdy byla prinyata ravnoi 10%. Stacionarnoe znachenie amplitudy okazalos' ravnym 18%. Amplituda kolebanii svetimosti vozrosla s 8% do 13% i tozhe ustanovilas' na etom urovne.

Na ris. 17 pokazano izmenenie skorosti dvizheniya sloev so vremenem i na raznyh glubinah. V bolee glubokih sloyah dvizheniya sinusoidal'ny, blizhe k poverhnosti amplituda kolebanii rastet, poyavlyayutsya vtorichnye maksimumy. Na ris. 18 pokazano izmenenie svetimosti na raznyh glubinah. Zdes' amplituda maksimal'na v zonah ionizacii, a blizhe k poverhnosti izmenenie svetimosti v techenie perioda opyat' umen'shaetsya. Krivaya svetimosti zametno nesinusoidal'na, s bolee krutym pod'emom i pologim umen'sheniem yarkosti.

Na ris. 19 dany diagrammy r - V(V = 1/r - udel'nyi ob'em) dlya raznyh zon. Ploshad' vnutri petli opredelyaet rabotu, vypolnennuyu gazom pri szhatii i razrezhenii v techenie odnogo perioda. Dissipaciya energii sootvetstvuet dvizheniyu vdol' cikla protiv chasovoi strelki, raskachka pul'sacii - dvizheniyu po chasovoi strelke (dvizhenie vdol' cikla ukazano strelkami). Na ris. 19 vidno, chto sloi 22 imeet polozhitel'nuyu dissipaciyu, no zdes' pul'sacii pochti adiabatichny (ploshad' petli mala). Etot sloi nahoditsya pod zonoi ionizacii geliya. V sloe 24 u osnovaniya zony chast' cikla imeet

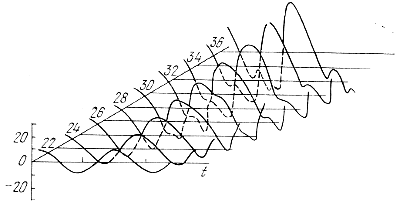
Ris. 17. Grafik izmeneniya skorosti dvizheniya sloev na raznyh glubinah v techenie odnogo perioda.
Chisla - nomera sloev (schet ot bolee glubokih sloev k poverhnosti). Amplituda maksimal'na vblizi poverhnosti.

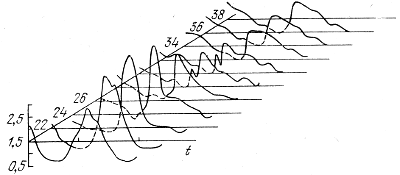
Ris. 18. Izmenenie svetimosti na raznyh glubinah v techenie odnogo perioda.
Amplituda izmenenii svetimosti maksimal'na na nekotoroi glubine.

polozhitel'nuyu dissipaciyu, chast' - otricatel'nuyu (eto sleduet iz perehlesta petli). V zonah ionizacii geliya (sloi 26 - 28) imeet mesto raskachka kolebanii otricatel'naya dissipaciya). V zone ionizacii vodoroda (sloi 32) takzhe proishodit raskachka kolebanii.

Podschet obshei ploshadi ciklov s raskachkoi pul'sacii pokazyvaet, chto 2/3 otricatel'noi dissipacii generiruetsya v zone ionizacii geliya, a odna tret' - v zone ionizacii vodoroda. Obe zony za odin period pul'sacii zabirayut iz potoka luchistoi energii, prohodyashei cherez eti sloi, 11 % energii. Iz etogo kolichestva 78% uhodit na pogashenie poter' energii pri kolebaniyah s polozhitel'noi dissipaciei bolee glubokih sloev (v samyh verhnih sloyah dissipaciya tozhe polozhitel'na, no ona mala), a 22% prevrashaetsya v kineticheskuyu energiyu. Takim obrazom, koefficient poleznogo deistviya pul'siruyushei zvezdy kak teplovoi mashiny raven 2,4% t. e. dostatochno mal.

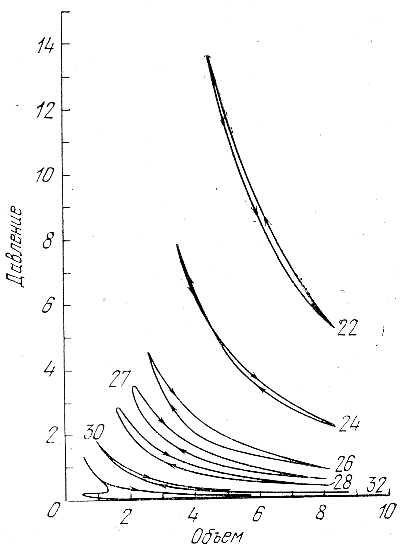
Ris. 19. Diagramma davlenie - ob'em dlya nekotoryh sloev v pul'siruyushei zvezde.
Ploshad' petli sootvetstvuet rabote za period. Dissipaciya energii - obhod protiv chasovoi strelki, raskachka kolebanii - obhod po chasovoi strelke. Shkala ordinat - davlenie v edinicah 10^-3 din/sm³, shkala absciss - ob'em sloya s sootvetstvuyushim nomerom v edinicah 10³³ g/ρ , gde ρ - plotnost' v etom sloe.

Hotya poka rasschitano eshe nemnogo modelei pul'sacii zvezd, mozhno sdelat' nekotorye kachestvennye i dazhe kolichestvennye vyvody o meste etih zvezd v obshem haraktere zvezdnoi evolyucii. Pul'siruyushie zvezdy prinadlezhat k vetvi krasnyh gigantov i zanimayut na diagramme Ressela - Gercshprunga dovol'no uzkuyu polosu. Po mere razvitiya krasnogo giganta iz goryachei zvezdy glavnoi posledovatel'nosti ee poverhnost' razduvaetsya i poverhnostnaya temperatura padaet. U goryachih zvezd vodorod i gelii ionizovany vplot' do samoi poverhnosti. Pri padenii poverhnostnoi temperatury obrazuyutsya ionizacionnye zony, kotorye pri dal'neishem ponizhenii T_eff okazyvayutsya pod ee poverhnost'yu. V etot moment sozdayutsya usloviya, blagopriyatnye dlya vozbuzhdeniya i podderzhaniya pul'sacii. Takim obrazom, pul'sirovat' zvezda nachinaet togda, kogda ee evolyucionnyi trek peresekaet oblast' na diagramme Ressela - Gercshprunga, v kotoroi zony ionizacii nahodyatsya nedaleko pod poverhnost'yu. Pri etom uskorenie sily tyazhesti zdes' dolzhno byt' otnositel'no neveliko.

Odnako vse chislennye raschety provodilis' dlya otdel'nyh konkretnyh modelei zvezd. Voznikaet vopros, mozhno li poluchit' kakie-libo kriterii podobiya, obshie sootnosheniya dlya parametrov pul'siruyushih zvezd? Ochevidno, chto pervym kriteriem podobiya sluzhit sootnoshenie (5.21), svyazyvayushee period so srednei plotnost'yu. Mozhno bylo by takzhe ozhidat', chto kriteriem podobiya yavlyaetsya i opredelenie (5.26) - pul'siruyushie zvezdy podobny, esli s u etih zvezd odinakovo. Velichina s zavisit ot dvuh harakteristik, kotorye legko opredelit', - perioda P i svetimosti L, i odnoi harakteristiki, kotoruyu trudnee ocenit', - teplovoi energii pul'siruyushego sloya U_k. V pervoi glave byl poluchen bezrazmernyi kompleks (formula (1.21)), kuda vhodila polnaya energiya zvezdy; tam bylo pokazano, chto etot kompleks sil'no menyaetsya u raznyh zvezd i poetomu ne mozhet byt' kriteriem podobiya. Veroyatno, i velichinu s iz (5.26) nel'zya rassmatrivat' kak kriterii podobiya. Po-vidimomu, eto svyazano s tem, chto v predelah vsei pul'siruyushei zony parametr s iz (5.26) menyaet znak i voobshe var'iruetsya v shirokih predelah.

Vprochem, v ryade rabot (sm. [3, 7]) predlagalsya kriterii podobiya vida

$\frac{LP}{M} = const,$ (5.36)

sleduyushii iz usloviya s = const, esli predpolozhit', chto otnositel'naya massa pul'siruyushego sloya bolee ili menee odinakova u vseh pul'siruyushih zvezd. Temperatura v zonah ionizacii tozhe odinakova i poetomu U_k ∼ ΔM ∼ M.

No v nastoyashee vremya usloviya podobiya pul'siruyushih zvezd obychno poluchayut putem obobsheniya rezul'tatov chislennyh raschetov. Naprimer, Iben [9] daet sleduyushuyu formulu, pozvolyayushuyu opredelit' period pul'sacii zvezd tipa RR Liry:

$\lg\left(\frac{P}{1 \mbox{sutki}}\right) = -0,340 + 0,825\left(\lg\frac{L}{L_\odot} - 1,7\right) - 0,63\left(\lg\frac{M}{M_\odot} + 0,19\right) - 3,34 \left(\lg\frac{T_{eff}}{10^4 K} + 0,15\right),$ (5.37)

gde T_eff - poverhnostnaya temperatura etih zvezd. V etom sootnoshenii mozhno pereiti ot T_eff k radiusu zvezdy, tak kak L = 4πσT⁴_effR², i vvesti srednyuyu plotnost'. Togda poluchim

$\lg P = -0,56\lg\bar\rho - 0,07\lg M - 0,01\lg L + const,$ (5.38)

v to vremya kak iz elementarnoi teorii podobiya sleduet $lg P = -0,5\lg\bar\rho + const$ . Itak, hotya nekotoraya zavisimost' kriteriya podobiya ot massy i svetimosti zvezdy est', no otkloneniya sravnitel'no neveliki.

Vtoroi kriterii podobiya, opredelyayushii usloviya raskachki i zatuhaniya pul'sacii, t. e. parametr s, dolzhen, voobshe govorya, svyazat' massu i svetimost' zvezd s himicheskim sostavom zon ionizacii, ibo imenno etot sostav i opredelyaet povedenie koefficienta poglosheniya. Iben [9] predlagaet sleduyushie formuly:

$\lg\frac{L}{L\odot} = 1,67 + 1,45(Y-0,3) - 0,081(\lg Z + 3) + 0,11 \left(0,8 - \frac{M}{M\odot}\right),$

$\lg\frac{M}{M\odot} = -0,194 + 0,073(Y-0,3) - 0,088(\lg Z + 3) + 0,04 \left(0,8 - \frac{M}{M\odot}\right),$

gde Y i Z - koncentracii geliya i tyazhelyh elementov sootvetstvenno. Pravda, Iben podcherkivaet, chto eti formuly mogut byt' ispol'zovany lish' dlya ochen' grubyh ocenok parametrov pul'siruyushih zvezd tipa RR Liry.

Voobshe nuzhno imet' v vidu, chto slozhnaya struktura real'nyh pul'siruyushih zvezd vryad li sposobstvuet nahozhdeniyu prostyh kriteriev podobiya dlya etih ob'ektov.

<< § 4.5 Chislennoe modelirovanie evolyucii zvezd | Oglavlenie | § 5.2 Vrashenie i magnitnye polya zvezd >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

$P(r) = \frac{2\pi}{\sqrt{(\Gamma - 1)[\beta\eta + 4(1-\beta)] + 3\beta\xi - 4}}\sqrt{\frac{r^3}{GM(r)}},$	(5.32)
$P(r) = \frac{2\pi}{\sqrt{\frac{3\alpha + 4 + 3m}{\nu + 4 - n}[\beta\eta + 4(1-\beta)] + 3\beta\xi - 4}}\sqrt{\frac{r^3}{GM(r)}},$	(5.33)