Astronet > Razmernosti i podobie astrofizicheskih velichin

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 5.2 Vrashenie i magnitnye polya zvezd | Oglavlenie | § 5.4 Cirkulyaciya v atmosferah planet >>

§ 5.3 Turbulentnost' i konvekciya

V fizike zvezd bol'shuyu rol' igraet yavlenie konvekcii. My uzhe videli v predydushei glave, chto konvektivnyi perenos energii sushestven kak v goryachih zvezdah (konvektivnye yadra), tak i v holodnyh (konvektivnye zony vblizi poverhnosti). Konvektivnye dvizheniya vblizi poverhnosti zvezd generiruyut zvukovye volny, nagrevayushie samye verhnie sloi atmosfery. Takim obrazom sozdayutsya hromosfera i korona Solnca i, po sushestvu, konvekciya nahoditsya v osnove vsego mnogoobraziya solnechnyh yavlenii.

K sozhaleniyu, yavlenie zvezdnoi konvekcii eshe daleko ot bolee ili menee polnogo teoreticheskogo ob'yasneniya. Delo v tom, chto zvezdnaya konvekciya v osnovnom imeet turbulentnyi harakter, a teoriya razvita preimushestvenno dlya sluchaya laminarnoi konvekcii. Tem ne menee udalos' poluchit' mnogo interesnyh rezul'tatov. Kak v teorii turbulentnosti, tak i v teorii konvekcii metody analiza razmernostei i teoriya podobiya igrayut ochen' bol'shuyu rol'. Poetomu kazhetsya umestnym dat' izlozhenie teh rezul'tatov teorii konvekcii i turbulentnosti, kotorye byli polucheny metodom analiza razmernostei ili teorii podobiya i kotorye mogut naiti ili uzhe nashli sebe primenenie v fizike zvezd i mezhzvezdnoi sredy. Snachala rassmotrim zakonomernosti turbulentnosti v obshem vide, ne specializiruya prichin, kotorye ee vyzyvayut.

Kak izvestno, turbulentnost'yu nazyvaetsya takoe sostoyanie sredy, pri kotorom vozbuzhdeny dvizheniya raznyh masshtabov, prichem imeet mesto perekachka energii mezhdu etimi dvizheniyami. V osnove yavleniya turbulentnosti lezhit stremlenie energii pereraspredelit'sya po bol'shomu chislu stepenei svobody. Dopustim, chto v nekotoroi srede bylo vozbuzhdeno dvizhenie veshestva bol'shogo masshtaba. Esli net vzaimodeistviya s dvizheniyami drugih masshtabov, to energiya etih krupnomasshtabnyh dvizhenii zatuhaet iz-za dissipativnyh processov, sohranyaya svoi harakternyi masshtab. No esli dvizheniya nelineinye, to energiya ot dvizhenii krupnyh masshtabov perehodit k dvizheniyam men'shih masshtabov, gde ona i dissipiruet v teplovuyu energiyu.

Razlichayut dva vida turbulentnosti - vihrevuyu i akusticheskuyu. V vihrevoi turbulentnosti, kak pokazyvaet samo nazvanie, dvizhenie veshestva imeet harakter vihrei razlichnogo masshtaba. Inymi slovami, v dvizheniyah vseh masshtabov

$rot v \ne 0.$ (5.82)

Mozhno vvesti harakternyi razmer vihrya l (ego diametr!) i sootvetstvuyushuyu skorost' vihrevogo dvizheniya v_l. Chasto vmesto masshtaba l vvodyat ponyatie o volnovom chisle vihrya k, kotoroe opredelyaetsya tak:

$k = \frac{2\pi}{l}.$ (5.83)

V akusticheskoi turbulentnosti dvizheniya imeyut harakter voln, t. e. eto dvizheniya potencial'nogo tipa. V strogo akusticheskoi turbulentnosti

$rot v = 0.$ (5.84)

Dvizhenie veshestva harakterizuetsya dlinoi voln ili volnovymi chislami, skorost'yu rasprostraneniya etih voln, kotoruyu my budem oboznachat' cherez v_s, a takzhe skorost'yu dvizheniya veshestva, kotoruyu budem oboznachat' cherez v_k. Esli volny imeyut lineinyi harakter (obychno pri v_k≪v_s), to vzaimodeistvie mezhdu volnami raznyh masshtabov nesushestvenno i akusticheskoi turbulentnosti ne voznikaet. Odnako pri bol'shoi amplitude voln (v_k ne slishkom malo po sravneniyu so skorost'yu zvuka) vzaimodeistvie mezhdu volnami raznyh masshtabov okazyvaetsya sushestvennym i energiya perekachivaetsya ot voln odnih masshtabov k volnam s drugimi masshtabami.

Osnovnoi harakteristikoi turbulentnosti yavlyaetsya se spektral'naya funkciya - raspredelenie energii po razlichnym masshtabam dvizheniya ili, chto odno i to zhe, zavisimost' skorosti dvizheniya ot masshtaba. Imenno dlya opredeleniya etih zavisimostei i mozhno ispol'zovat' metod analiza razmernostei.

V vihrevoi turbulentnosti imeet mesto horosho izvestnyi spektr Kolmogorova. Strogo govorya, etot spektr poluchen dlya chastnogo sluchaya izotropnoi i odnorodnoi turbulentnosti neszhimaemoi zhidkosti. No mnogochislennye eksperimenty pokazali ego universal'nost' i primenimost' k usloviyam, ves'ma dalekim, ot odnorodnosti i izotropnosti.

Spektr Kolmogorova osnovan na predpolozhenii, chto perekachka energii mezhdu vihryami razlichnyh masshtabov opredelyaetsya tol'ko odnim parametrom ε - potokom energii cherez vsyu ierarhiyu vihrei, ot samyh bol'shih k samym malym. Esli schitat', chto energiya krupnomasshtabnyh dvizhenii ne dissipiruet neposredstvenno v teplo, to velichina energii, peredavaemaya ot vihrei etogo masshtaba k vihryam men'shego masshtaba, postoyanna, t. e. ne zavisit ni ot masshtaba dvizhenii, ni ot sootvetstvuyushih skorostei. Razmernost' potoka energii, otnesennaya k edinice massy, est'

$rot v = 0.$ (5.85)

Predpolozhim, chto dvizhenie v nekotoryh masshtabah l ne zavisit ot drugih parametrov, krome ε . Togda zavisimost' v_l ot l mozhet byt' poluchena putem sostavleniya bezrazmernogo kompleksa iz velichin ε , l i v_l. Uchityvaya (5.85), srazu poluchaem s tochnost'yu do chislennogo mnozhitelya:

$v_l \sim (\epsilon l)^{1/3}.$ (5.86)

Opredelim spektral'nuyu funkciyu energii turbulentnogo dvizheniya W_k takim obrazom, chtoby energiya, zaklyuchennaya v dvizheniyah s volnovymi chislami v intervale ot k do k + dk, ravnyalas' W_kdk. Togda iz (5.86) sleduet

$W_k \sim \frac{\rho \epsilon^{2/3}}{k^{5/3}},$ (5.87)

gde ρ - plotnost' sredy. Sootnosheniya (5.86) i (5.87) i est' spektr Kolmogorova.

Spektr Kolmogorova nel'zya primenyat' neposredstvenno k dvizheniyam samyh bol'shih masshtabov - zdes' ε uzhe ne yavlyaetsya edinstvennym opredelyayushim parametrom. V chastnosti, skorosti dvizheniya v etih masshtabah zavisyat i ot geometrii sredy i ot toi prichiny, kotoraya vyzyvaet dvizheniya v samyh krupnyh masshtabah. So storony malyh masshtabov spektr Kolmogorova ogranichen vliyaniem vyazkosti ili drugih dissipativnyh processov. Pust' ν - kinematicheskii koefficient vyazkosti ili drugogo dissipativnogo processa, kotoryi mozhet vliyat' na harakter dvizheniya. Ego razmernost'

$[\nu] = \left[\frac{\eta}{\rho}\right] = \frac{\mbox{sm}^3}{\mbox{sek}}.$ (5.88)

Togda nizhnyaya granica kolmogorovskogo spektra l_ν opredelyaetsya sovmestnym deistviem ε i ν. Sostavlyaya bezrazmernuyu kombinaciyu iz etih velichin i masshtaba l_ν, poluchim

$l_\nu \sim \left(\frac{\nu^3}{\epsilon}\right)^{1/4}.$ (5.89)

Real'naya vihrevaya turbulentnost' v kosmicheskih usloviyah, konechno, ne yavlyaetsya ni izotropnoi, ni odnorodnoi, i imeet mesto v szhimaemom, gaze. Tem ne menee pse eti sootnosheniya, imeyushie razmernostnyi harakter, ostayutsya spravedlivymi.

Privedem neskol'ko konkretnyh primerov. Na ris. 20 privedena velichina energii dvizheniya mezhzvezdnoi sredy W(l) kak funkciya masshtaba dvizheniya l. Iz (5.87) sleduet sootnoshenie

$W(l) \approx \rho v_l^2 \approx \rho(\epsilon l)^{2/3},$

spravedlivoe dlya ne slishkom bol'shih masshtabov.

Nablyudaemaya zavisimost' okazalas' neskol'ko bolee krutoi, W(l) ∼ l^0,7, [14], no blizkoi k teoreticheskomu spektru Kolmogorova, hotya, konechno, dvizheniya mezhzvezdnogo gaza ne yavlyayutsya ni izotropnymi, ni odnorodnymi. Velichina l₀ ≈ 80 - 100 ps harakterizuet masshtab dvizhenii s maksimal'noi plotnost'yu energii. Dalee s rostom l plotnost' energii bystro spadaet.

Podobnye spektry byli polucheny i dlya dvizhenii v tumannosti Oriona [15]. Voobshe razlichnye issledovaniya povedeniya skorostei v turbulentnyh astrofizicheskih sredah pokazyvayut, chto po krainei mere ne v ochen' krupnyh masshtabah dvizhenii imeet mesto spektr Kolmogorova. K sozhaleniyu, postroenie spektrov dvizhenii gaza v kosmicheskih ob'ektah chasto zatrudneno tem, chto odnovremennye opredeleniya iz nablyudenii skorostei dvizheniya razlichnyh masshtabov ochen' slozhny.

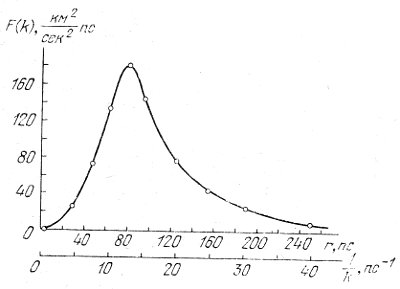
Ris. 20. Spektral'naya funkciya mezhzvezdnoi turbulentnosti.
Spektru Kolmogorova sootvetstvuet voshodyashaya chast' krivoi (do 80 ps).

Razmernostnoe sootnoshenie (5.86) okazyvaetsya ochen' poleznym i dlya ocenki dissipacii energii v turbulentnyh dvizheniyah v teh sluchayah, kogda mozhno opredelit' po dannym nablyudenii skorost' dvizhenii i masshtab. Dlya turbulentnosti mezhzvezdnoi sredy imeem v = 7 km ⋅ sek^-1 i l ≈ 100 ps ≈ 3 ⋅ 10²⁰ sm, otkuda poluchaem ε = 10^-3 erg ⋅ g^-1 ⋅ sek^-1. Takoe kolichestvo energii dolzhno postavlyat'sya istochnikami, vozbuzhdayushimi mezhzvezdnuyu turbulentnost'.

V kachestve drugogo primera ocenim harakternye velichiny krupnomasshtabnyh dvizhenii v zvezdnoi atmosfere, voznikayushih iz-za turbulentnoi konvekcii. Harakternyi razmer naibolee krupnomasshtabnogo vihrya ne mozhet zametno prevyshat' ekvivalentnuyu vysotu sloya - v protivnom, sluchae v odnom i tom zhe masshtabe dvizheniya proishodilo by ochen' sil'noe izmenenie plotnosti. Poetomu

$l_0 \approx \frac{\Re T}{\mu g},$ (5.90)

gde T - temperatura sloya i g - uskorenie sily tyazhesti. Skorost' dvizhenii v₀ opredelyaetsya potokom kineticheskoi energii, kotoruyu eti dvizheniya dolzhny perenosit', t. e. velichinoi

$F_{\mbox{kin}} = \frac{L}{4\pi R^2} \approx \rho v_0^3.$ (5.91)

Zdes' schitaetsya, chto v oblasti konvekcii zametnaya chast' polnogo potoka energii L/4πR² perenositsya gazodinamicheskimi dvizheniyami, skorosti kotoryh v₀, a plotnosti energii ρv₀² (nizhe budet privedena formula (5.154) dlya potoka teplovoi energii, perenosimoi konvekciei). Podstavlyaya l₀ iz (5.90) i v₀ iz (5.91) v sootnoshenie (5.86), opredelim dissipaciyu energii v sloyah zvezdy s sushestvennym konvektivnym perenosom energii:

$\epsilon \approx \frac{Lg\mu}{4\pi R^2\rho\Re} \approx \frac{GML}{4\pi R^4p},$ (5.92)

gde p - davlenie gaza v konvektivnoi zone. Na Solnce velichina ε poryadka 10¹² sm² ⋅ sek^-3, u sverhgigantov mnogo men'she, poryadka 10⁶ sm² ⋅ sek^-3. No u vspyhivayushih zvezd i krasnyh karlikov velichina e mozhet byt' i sushestvenno bol'she, poryadka 10¹⁴ sm² ⋅ sek^-3.

Pereidem teper' k sluchayu akusticheskoi turbulentnosti. Zdes', krome togo zhe osnovnogo parametra ε - dissipacii energii, est' eshe odin opredelyayushii parametr: v_s - skorost' rasprostraneniya zvukovyh voln. Iz chetyreh velichin s razmernostyami, zavisyashimi tol'ko ot dliny i vremeni:

$\begin{array}{l} [\epsilon] = \mbox{sm}^2 \cdot \mbox{sek}^{-3},\\ {[l]} = \mbox{sm} \\ {[v_s]} = [v_l] = \mbox{sm} \cdot \mbox{sek}^{-1}, \end{array}$ (5.93)

mozhno sostavit' dva bezrazmernyh kompleksa i, sledovatel'no, na osnovanii odnih soobrazhenii analiza razmernostei nel'zya poluchit' spektr akusticheskoi turbulentnosti. No eto mozhno vse zhe sdelat', ispol'zuya nekotorye dopolnitel'nye fizicheskie soobrazheniya.

Vo-pervyh, nado uchest', chto esli v vihrevoi turbulentnosti kazhdyi vihr' zhivet primerno stol'ko vremeni, skol'ko nuzhno veshestvu, chtoby sovershit' odin polnyi oborot (t. e. v vihrevoi turbulentnosti harakternoe vremya τ ∼ l/v_l), to v akusticheskoi turbulentnosti volna sushestvuet neskol'ko ili dazhe mnogo periodov. Inymi slovami, zdes' harakternoe vremya dvizheniya v masshtabe l dolzhno byt' mnogo bol'she velichiny "vremeni obrasheniya", t. e. velichiny l/v_l.

Vzaimodeistvie voln mezhdu soboi opredelyaetsya ih nelineinost'yu, t. e. velichinoi otnosheniya v_l/v_s. Budem, poetomu schitat', chto v pervom priblizhenii harakternoe vremya vzaimodeistviya τ bol'she vremeni obrasheniya na mnozhitel' poryadka bol'shoi velichiny otnosheniya v_s/v_l t. e.

$\tau \approx \frac{v_s}{v_l}\frac{l}{v_l} \approx \frac{v_s}{kv_k^2}.$ (5.94)

Potok energii cherez "ierarhiyu voln", rasschitannyi na edinicu massy, ochevidno, raven

$\epsilon \approx \frac{v_l^2}{\tau} \approx \frac{v_l^4}{v_s l} \approx \frac{kv_k^4}{v_s}.$ (5.95)

Po-prezhnemu budem schitat', chto turbulentnost' opredelyaetsya tol'ko peredachei energii ot odnih masshtabov k drugim i chto dissipaciya energii v teplo proishodit v samyh malyh masshtabah. Togda velichinu ε mozhno schitat' postoyannoi, i poetomu

$v_l \sim (\epsilon v_s l)^{1/4}.$ (5.96)

Spektral'naya funkciya akusticheskoi turbulentnosti [16]:

$v_l \sim (\epsilon v_s l)^{1/4}.$ (5.97)

Minimal'nyi masshtab (minimal'naya dlina volny) opredelyaetsya sootnosheniem (5.89).

Analiz spektrov akusticheskoi (mln magnitozvukovoi) turbulentnosti v astrofizicheskih usloviyah poka eshe ne provodilsya. Poetomu my ogranichimsya lish' nekotorymi kachestvennymi zamechaniyami. Sootnoshenie (5.96), tak zhe kak i (5.86), mozhno ispol'zovat' dlya ocenki energii turbulizacii. Sravnivaya eti formuly, vidim, chto v sluchae zvukovoi turbulentnosti neobhodim men'shii rashod energii na vozbuzhdenie dvizhenii s temi zhe skorostyami i v teh zhe masshtabah, chto i v sluchae vihrevoi turbulentnosti. Eto oznachaet, chto esli perenos energii v atmosfere zvezdy opredelyalsya by volnami, to velichina (5.92) byla by men'she na mnozhitel' v₀/v_s. Na Solnce deistvitel'no imeetsya perenos energii volnami, no nuzhno imet' v vidu, chto takim putem perenositsya lish' nebol'shaya chast' polnogo potoka energii Solnca, t. e. ta chast', kotoraya rashoduetsya na nagrev hromosfery i korony.

Zadavaya i v etom sluchae potok energii F_a (kotoryi teper' mnogo men'she velichiny L/4πR²), poluchim vmesto (5.91)

$F_{\mbox{voln}} \approx \rho v_0^2v_s,$ (5.98)

poskol'ku teper' energiya perenositsya so skorost'yu zvuka. Podstavlyaya (5.90) i (5.98) v (5.96), nahodim

$\epsilon \approx \frac{v_0^4}{v_s l_0} \approx \frac{F_a^2\mu g}{\rho v_s^3\Re T} \approx \frac{GMF_a^2}{v_s R^2 p^2}$ (5.99)

s tochnost'yu do mnozhitelei poryadka edinicy.

Iz sopostavleniya (5.92) i (5.99) mozhno sdelat' sleduyushee zaklyuchenie. Pust' u nas est' konvekciya v vide turbulentnosti vihrevogo tipa, kotoraya na nekotorom urovne prevrashaetsya v zvukovuyu turbulentnost'. Togda ochevidno, chto pa etom urovne velichiny (5.92) i (5.99) dolzhny byt' odnogo poryadka. Priravnivaya eti velichiny, nahodim potok energii, perenosimyi volnovoi turbulentnost'yu:

$F_{\mbox{voln}} \approx \left(\frac{v_s pL}{4\pi R^2}\right)^{1/2} \approx \left(\frac{\Re T}{\mu}\right)^{3/4} \left(\frac{\rho L}{4\pi R^2}\right)^{1/2}.$ (5.100)

Dlya solnechnoi atmosfery imeem F_a ≈ 10⁷ erg ⋅ sm^-2 ⋅ sek^-1 v udovletvoritel'nom kachestvennom soglasii s dannymi nablyudenii.

Hromosfery, nagrevaemye volnovoi turbulentnost'yu, veroyatno, est' i u drugih zvezd. Mozhno ocenit' parametry zvezdy, u kotoroi hromosfernaya svetimost' L_a budet poryadka fotosfernoi svetimosti. Imeem

$\frac{L_{\mbox{voln}}}{L} = \frac{4\pi F_a R^2}{L} \approx \left(\frac{4\pi R^2 v_s p}{L}\right)^{1/2} \approx \left(\frac{\Re T}{\mu}\right)^{3/4} \left(\frac{4\pi R^2 \rho}{L}\right)^{1/2}$ (5.101)

gde, po-prezhnemu, r i ρ - davlenie i plotnost' v oblasti generacii volnovoi turbulentnosti. Poetomu blagopriyatnymi yavlyayutsya usloviya v krasnyh karlikah, u kotoryh deistvitel'no obnaruzheny hromosfernye linii.

Svoistva turbulentnosti chasto opredelyayut chislom Reinol'dsa dlya dannogo masshtaba dvizhenii. Dlya vihrevoi i akusticheskoi turbulentnosti sootvetstvenno imeem

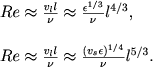
$\begin{array}{l} Re \approx \frac{v_l l}{\nu} \approx \frac{\epsilon^{1/3}}{\nu}l^{4/3}, \\ \\ Re \approx \frac{v_l l}{\nu} \approx \frac{(v_s \epsilon)^{1/4}}{\nu}l^{5/3}. \end{array}$

Velichina chisla Reinol'dsa est' otnoshenie vremeni dissipacii dvizhenii iz-za vyazkosti ∼ l²/v k harakternomu vremeni izmeneniya sostoyaniya dvizheniya v masshtabe l, t. e. velichine l/v_l ≈ l²/v_ll.

Chislo Reinol'dsa maksimal'no v oblasti dvizhenii osnovnogo masshtaba i minimal'no v oblasti masshtabov vyazkoi dissipacii energii. Esli formal'no v vyrazhenii dlya chisla Reinol'dsa podstavit' l iz (5.89), to poluchim, chto v oblasti masshtabov vyazkoi dissipacii Re ≈ 1. Odnako mnogochislennye eksperimental'nye dannye pokazali, chto dissipaciya energii turbulentnyh dvizhenii v teplovuyu iz-za deistviya vyazkosti nachinaetsya pri sushestvenno bol'shih masshtabah. Okazalos', chto v oblasti naibol'shei dissipacii chislo Reinol'dsa okolo 30-50. Otsyuda, vo-pervyh, sleduet, chto znachenie minimal'nogo masshtaba spektra Kolmogorova poryadka (15-25) (ν³/ε)^1/4. Vo-vtoryh, eto obstoyatel'stvo pozvolyaet poluchit' chislennuyu ocenku velichiny tak nazyvaemoi turbulentnoi vyazkosti. Eto yavlenie zaklyuchaetsya v sleduyushem.

Raspad dvizhenii osnovnogo masshtaba na bolee melkomasshtabnye dvizheniya mozhno opisat' s pomosh'yu dissipacii krupnomasshtabnyh dvizhenii pod deistviem turbulentnoi vyazkosti. Zdes' melkomasshtabnye dvizheniya igrayut rol' "molekul" s dlinoi svobodnogo probega l i skorost'yu dvizheniya v_l. Velichinu turbulentnoi vyazkosti ν_t vybirayut tak, chtoby chislo Reinol'dsa dlya turbulentnoi vyazkosti

$Re_t \approx \frac{v_0l_0}{v_t}$ (5.102)

tozhe bylo by okolo 30-50.

Esli turbulentnost' proishodit v elektroprovodyashei srede, gde est' hotya by slabye magnitnye polya, to ona okazyvaetsya tesno svyazannoi s magnitnym polem. V chastnosti, mnogo vnimaniya v astrofizike udelyalos' usileniyu magnitnogo polya turbulentnost'yu (turbulentnoe dinamo). Etoi probleme posvyashen, naprimer, obzor S. I. Vainshteina i Ya. B. Zel'dovicha [17]. Privedem lish' kratkuyu svodku poluchennyh v etom napravlenii rezul'tatov.

Prezhde vsego bylo pokazano, chto turbulentnye dvizheniya mogut usilivat' pervonachal'noe (zatravochnoe) magnitnoe pole, esli eta turbulentnost' girotropna, t. e. esli srednee znachenie skalyarnogo proizvedeniya skorosti na ee rotor ne ravno nulyu. Naglyadno etot effekt svoditsya k geometrii dvizhenii, kogda magnitnaya petlya "perehlestyvaetsya i skladyvaetsya", chto i privodit k rostu plotnosti magnitnyh silovyh linii.

Rost magnitnogo polya opredelyaetsya parametrom girotropnosti:

$\alpha_l = -\langle v_l \mathrm{rot} v_l\rangle\frac{\tau_l}{3} \ne 0,$ (5.103)

gde τ_l - harakternoe vremya korrelyacii dvizhenii (vremya raspada ili zatuhaniya dvizheniya v sootvetstvuyushem masshtabe). Magnitnoe pole usilivaetsya v teh masshtabah, gde parametr α_l ne mal po sravneniyu so skorost'yu v_l.

Naprimer, harakternoe vremya usileniya magnitnogo polya v akusticheskoi turbulentnosti:

$\alpha_l = -\langle v_l \mathrm{rot} v_l\rangle\frac{\tau_l}{3} \ne 0,$ (5.104)

t. e. bol'she vremeni perekachki energii mezhdu volnami raznyh masshtabov v (v_s/v_l)² raz.

V obzore [17] v osnovnom, rassmatrivaetsya sluchai, kogda dazhe usilennoe magnitnoe pole ostaetsya nastol'ko slabym, chto ne menyaet sushestvenno svoistva turbulentnosti.

Sluchai, kogda plotnosti kineticheskoi i magnitnoi energii v odnih i teh zhe masshtabah dvizheniya sravnimy, do sih por ne udalos' rassmotret' s neobhodimoi uverennost'yu v pravil'nosti poluchennyh rezul'tatov, nesmotrya na bol'shie usiliya, predprinyatye dlya resheniya etoi ochen' vazhnoi dlya astrofiziki problemy. Kachestvenno mozhno ukazat' na sleduyushie soobrazheniya. Esli magnitnoe pole V ochen' sil'noe, to vihrevye dvizheniya podavleny, i turbulentnost' togda mozhet vozniknut' lish' v vide sovokupnosti al'venovskih i magnitozvukovyh voln. Svoistva takoi turbulentnosti blizki k svoistvam akusticheskoi turbulentnosti i budut spravedlivy sootnosheniya (5.96) i (5.97), v kotoryh skorost' zvuka sleduet zamenit' na al'venovskuyu skorost' $B/\sqrt{4\pi\rho}$ . Poluchim dlya skorosti, sootvetstvuyushei amplitudam kolebanii gaza:

$v_l \sim \left(\frac{\epsilon B}{\sqrt{4\pi\rho}}l\right)^{1/4},$ (5.105)

i dlya spektral'noi plotnosti energii

$W_k \sim \rho^{3/4}\frac{(B\epsilon)^{1/2}}{k^{3/2}}.$ (5.106)

Esli zhe magnitnoe pole takovo, chto plotnost' ego energii v bol'shih masshtabah neskol'ko men'she, chem plotnost' kineticheskoi energii, to takoe magnitnoe pole kak by podavlyaet dvizhenie v melkih masshtabah i spektr stanovitsya bolee krutym, [14]. V rabote [17] iz evristicheskih soobrazhenii poluchen spektr dvizhenii

$W_k \sim \frac{const}{k^2}.$ (5.107)

Spektr takogo tipa poluchaetsya voobshe v teh sluchayah, kogda energiya dvizheniya krupnyh masshtabov ne perehodit v melkomasshtabnye dvizheniya, naprimer, esli ona dissipiruet v krupnomasshtabnyh udarnyh volnah (sm. [14] i [18]).

V knige B. B. Kadomceva [19] dano yasnoe i fizicheski naglyadnoe opisanie svoistv turbulentnosti v razlichnyh usloviyah.

Posle etogo obsuzhdeniya obshih svoistv turbulentnosti mozhno pereiti k analizu konvekcii.

Nam uzhe izvestno, chto konvekciya voznikaet togda,, kogda sloi gaza dolzhen perenesti dostatochno bol'shoi potok energii snizu vverh (protiv napravleniya uskoreniya sily tyazhesti), a luchistaya ili drugie vidy teploprovodnosti ne v sostoyanii etogo sdelat', naprimer, iz-za slishkom bol'shoi neprozrachnosti. Pri konvekcii vnizu etogo sloya obrazuyutsya bolee nagretye elementy gaza, kotorye vsplyvayut vverh, perenosya izbytok teplo-voi energii, otdayut ego v verhnei chasti sloya i zatem opuskayutsya vniz uzhe holodnymi elementami. Takim obrazom, konvekciyu mozhno oharakterizovat' skorost'yu konvektivnyh elementov i dlinoi ih probega. Eti dve velichiny pozvolyayut vychislit' chisla Reinol'dsa, - kak pravilo, v kosmicheskih usloviyah oni okazyvayutsya ochen' bol'shimi, dostigaya znachenii poryadka 10¹⁰ ili dazhe bol'she. Imenno poetomu mozhno ozhidat', chto astrofizicheskaya konvekciya v bol'shinstve sluchaev dolzhna byt' turbulentnoi. Snachala izbytok tepla v nizhnem sloe peredaetsya dvizheniyam tipa bol'shih vihrei, kotorye sushestvuyut ne bol'she, chem vremya dvizheniya gaza po okruzhnosti vihrya i poetomu ne uspevayut donesti izbytok tepla do verhnei granicy sloya. Krupnomasshtabnye vihri raspadayutsya na melkomasshtabnye, vsya oblast' turbulentnoi konvekcii sostoit iz bol'shogo chisla raznomasshtabnyh vihrei i potok tepla lish' posledovatel'no peredaetsya ot nizhnei granicy sloya k verhnei. Peli zhe chislo Reinol'dsa neveliko, to voznikaet laminarnaya konvekciya, kotoraya imeet drugoi harakter. Zdes' dvizhenie gaza bolee plavnoe, ono kontroliruetsya, s odnoi storony, vsplyvaniem konvektivnyh elementov iz-za izbytka tepla, a s drugoi storony, tormozheniem etogo dvizheniya iz-za vyazkosti i teploprovodnosti. V podobnoi konvekcii dvizhenie stacionarno, vmesto bol'shogo kolichestva raznomasshtabnyh vihrei obrazuyutsya bolee ili menee odinakovye, raspolozhennye pravil'nym, obrazom, konvektivnye yacheiki, vysota kotoryh ravna tolshine konvektivnoi zony, a ih gorizontal'nyi razmer svyazan s vysotoi opredelennym sootnosheniem. V predelah odnoi i toi zhe yacheiki gaz mozhet sovershit' mnogo oborotov prezhde, chem yacheika ischeznet. Mozhno schitat', chto v ideal'nom sluchae stacionarnyi sloi laminarnoi konvekcii sostoit iz stacionarnyh yacheek, v kotoryh gaz techet po zamknutym liniyam toka, nagrevayas' vnizu i ohlazhdayas' vverhu. Takie yacheiki imeyut pravil'nuyu formu, chashe vsego shestiugol'nyh prizm.

Teoriya laminarnoi konvekcii byla dostatochno polno razvita primenitel'no k konvekcii v odnorodnom sloe neszhimaemoi zhidkosti (sm. podrobnoe izlozhenie v knige Chandrasekara [20]), no eti rezul'taty mozhno ispol'zovat' i dlya analiza konvekcii v szhimaemom i neodnorodnom sloe gaza, esli tol'ko na vertikal'nom protyazhenii sloya plotnost' gaza ne menyaetsya sushestvennym obrazom. Eto sootvetstvuet sluchayu tak nazyvaemogo priblizheniya Bussineska. Rassmotrim etot sluchai bolee podrobno.

Laminarnaya konvekciya opisyvaetsya ryadom bezrazmernyh chisel, kotorye mozhno poluchit' i pz soobrazhenii analiza razmernostei. Razumeetsya, dlya nahozhdeniya sootnoshenii mezhdu bezrazmernymi parametrami odin analiz razmernostei nedostatochen i prihoditsya ispol'zovat' uravneniya dvizheniya. V sootvetstvii s cel'yu etoi knigi my poluchim bezrazmernye kompleksy laminarnoi konvekcii na osnove teorii razmernostei i podobiya, a zatem privedem i nekotorye sootnosheniya mezhdu razlichnymi bezrazmernymi kompleksami, harakterizuyushimi laminarnuyu konvekciyu.

Nachnem so sluchaya konvekcii v srede, gde net vrasheniya i magnitnogo polya, i gde kazhdyi konvektivnyi element gaza neprozrachen. Inymi slovami, budem schitat', chto obmen energiei mezhdu podnimayushimisya i opuskayushimisya potokami gaza proishodit preimushestvenno na poverhnosti razdela etih potokov. Vse eti ogranicheniya budem potom snimat' po ocheredi.

Naidem opredelyayushie parametry takoi zadachi. Dlya etogo napomnim fiziku konvektivnogo dvizheniya. Pust' est' nekotoryi gradient temperatury (temperatura padaet snizu vverh). Togda, esli kakoi-to element gaza podnimaetsya, to on, okazavshis' v sloe s men'shei temperaturoi, rasshiryaetsya iz-za umen'sheniya vneshnego davleniya i pri etom stanet menee plotnym. Okazavshis' legche okruzhayushih sloev, konvektivnyi element gaza prodolzhaet pod'em, poka on ne doidet do verhnei granicy konvektivnogo sloya, gde izbytok tepla budet otdan verhnim sloyam. Ochevidno, chto effekt perenosa energii opredelyaetsya sleduyushimi yavleniyami: teploprovodnost'yu; siloi, zastavlyayushei gaz dvigat'sya, t. e. siloi Arhimeda, i siloi, tormozyashei dvizhenie, t. e. vyazkost'yu. Eti soobrazheniya pozvolyayut naiti opredelyayushie parametry.

Sila Arhimeda est' proizvedenie uskoreniya sily tyazhesti na izmenenie plotnosti br nagretogo elementa gaza po sravneniyu s okruzhayushei sredoi. My budem otnosit' vse sily k edinice massy i poetomu otnositel'naya sila Arhimeda est' - g(δρ/ρ). Plotnost' gaza umen'shaetsya iz-za ego nagrevaniya i poetomu luchshe izmenenie plotnosti vyrazit' cherez izbytok temperatury δ T. Esli vvesti koefficient teplovogo rasshireniya a, to imeem δρ/ρ = -αδT. V ideal'nom gaze koefficient tep- lovogo rasshireniya opredelyaetsya ochen' prostoi formuloi: α = 1/T. Nakonec, izbytok temperatury δ T sleduet vyrazit' cherez tak nazyvaemyi sverhadiabaticheskii temperaturnyi gradient:

$\beta = \frac{dT}{dz}-\left(\frac{dT}{dz}\right)_{ad},$ (5.108)

gde dT/dz - srednii gradient temperatury v sloe, (dT/dz)_ad - adiabaticheskii gradient temperatury v podnimayushemsya elemente gaza. Konvekciya vozmozhna tol'ko esli β > 0. Imenno sverhadiabaticheskii gradient i opredelyaet otnositel'nuyu "legkost'" podnimayushihsya konvektivnyh elementov.

Takim obrazom, parametr, harakterizuyushii silu Arhimeda pri konvekcii, mozhno zapisat' v vide

$-g\frac{\delta\rho}{\rho} = g\alpha\delta T = g\alpha\beta l,$ (5.109)

gde l - tolshina konvektivnoi zony. Dva drugih opredelyayushih parametra - vyazkost' i teploprovodnost', - harakterizuyutsya koefficientami kineticheskoi vyazkosti ν i temperaturoprovodnosti χ . Oba koefficienta imeyut odinakovuyu razmernost'

$[\nu] = [\chi] = \mbox{sm}^2 \cdot \mbox{sek}^{-1}.$ (5.110)

Iz-za odinakovoi razmernosti sushestvuet nekotoraya neopredelennost' v ispol'zovanii etih koefficientov, no, kak okazalos', zdes' vse_opredelyaetsya ih srednim geometricheskim znacheniem $\sqrt{\nu\chi}$ . Opredelyayushim parametrom yavlyaetsya i tolshina konvektivnogo sloya. Itak, imeem sleduyushii nabor opredelyayushih parametrov:

$\begin{array}{l} [g\alpha\beta l] = \mbox{sm} \cdot \mbox{sek}^{-2},\\ {[\sqrt{\nu\chi}]} = \mbox{sm}^2 \cdot \mbox{sek}^{-1} \\ {[l]} = \mbox{sm}. \end{array}$ (5.111)

Otsyuda srazu nahodim bezrazmernyi kompleks - chislo Releya:

$R = \frac{g\alpha\beta l^4}{\nu\chi}.$ (5.112)

Legko ubedit'sya, chto chislo Releya est' obratnoe otnoshenie kvadratov harakternogo vremeni vsplyvannya i vremeni dissipacii.

Poetomu chislo Releya sootvetstvuet kvadratu chisla Reinol'dsa dlya konvektivnogo dvizheniya. Eto oznachaet, chto chislennoe znachenie (5.112) dlya sluchaya laminarnoi konvekcii dolzhno byt' poryadka 10³, poskol'ku sootvetstvuyushee chislo Reinol'dsa dlya dvizhenii opredelyaemyh vyazkost'yu, poryadka 30.

Zadachu o vychislenii chisla Releya mozhno reshit' tochno v prostom sluchae odnorodnoi neszhimaemoi zhidkosti. Privedem zdes' etot raschet, hotya, konechno, astrofizicheskie usloviya daleki ot sluchaya neszhimaemoi zhidkosti.

Budem rassmatrivat' stacionarnye dvizheniya podnimayushegosya elementa gaza. Uravneniya dvizheniya zapishutsya v vide:

$R = \frac{g\alpha\beta l^4}{\nu\chi}.$ (5.113)

Zdes' $\vec v$ - vektor skorosti, Δ - operator Laplasa, δp - izbytok davleniya v podnimayushemsya elemente gaza. Pervoe uravnenie est' obychnoe uravnenie dvizheniya s vyazkost'yu i arhimedovoi siloi, vtoroe uravnenie est' uravnenie temperaturoprovodnosti v dvizhusheisya srede.

Budem reshat' (5.113) posledovatel'nymi priblizheniyami. V pervom priblizhenii opustim vse chleny s $\vec v$ , δp i δρ. Pervoe uravnenie budet udovletvoreno avtomaticheski, vtoroe uravnenie, pri uslovii, chto temperatura zavisit tol'ko ot vertikal'noi koordinaty z, daet

$T = T_0 - \beta z,$ (5.114)

gde T₀ - temperatura na nizhnei granice sloya. Zdes' β est' nekotoraya postoyannaya, opredelyayushaya stacionarnyi gradient temperatury v sloe. Ochevidno, chto pri stacionarnoi konvekcii velichina β est' sverhadiabaticheskii temperaturnyi gradient (5.108). V sleduyushem priblizhenii uchtem v (5.114) izmenenie temperatury v podnimayushihsya i opuskayushihsya elementah, t. e. zapishem

$T = T_0 - \beta z + \delta T.$ (5.115)

Podstavim (5.115) vo vtoroe uravnenie (5.113) i poluchim, sohraniv lish' chleny pervogo poryadka malosti,

$v_z\beta + \chi\Delta(\delta T) = 0.$ (5.116)

V pervom uravnenii zamenim δρ/ρ na α(δT). Levaya chast' - vtorogo poryadka malosti, ee mozhno opustit' i v etom priblizhenii. Chtoby isklyuchit' chlen $\mathrm{grad}\left(\frac{\delta p}{\rho}\right)$ , primenim k etomu uravneniyu operaciyu rotora. Togda poluchim

$\nu\Delta\mathrm{rot}\,\vec v + \alpha\,\mathrm{rot}(\vec{g}\delta T) = 0.$ (5.117)

Eshe raz primenim k etomu uravneniyu operaciyu rotora i uchtem, chto v sluchae neszhimaemoi zhidkosti $\mathrm{rot}\,\mathrm{rot}\,\vec v = \mathrm{grad}\,\mathrm{div}\,\vec v - \Delta\vec v = -\Delta\vec v$ , tak kak zdes' $\mathrm{div}\vec v = 0$ . Togda poluchim vmesto (5.117)

$-\nu\Delta\Delta\vec v + \alpha\,\mathrm{rot}\,\mathrm{rot}(\vec g\delta T) = 0.$

V etom uravnenii predstavlyaet interes lish' vertikal'naya komponenta. Vychislyaya vtoroi chlen uravneniya, nahodim

$\nu\Delta\Delta v_z = -\alpha g\left[\left(\frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}\right)\delta T\right].$ (5.118)

Nakonec, podstavim v (5.118) velichinu v_z iz (5.116) i poluchim sleduyushee uravnenie dlya izbytka temperatury v podnimayushihsya i opuskayushihsya elementah gaza:

$\Delta\Delta\Delta\delta T = \left[\left(\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}\right)^3\delta T\right] = \frac{\alpha\rho g}{\chi\nu} \left[\left(\frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}\right)\delta T\right].$ (5.119)

Lyubopytno, chto zdes' ponadobilos' tri raza ispol'zovat' operator Laplasa.

Teper' ostalos' sformulirovat' granichnye usloviya. Zdes' vozmozhna razlichnaya postanovka zadach. Vo-pervyh, vo vseh sluchayah na granice dolzhno byt' v_z = 0, a sledovatel'no, i δ T = 0. Veshestvo ne mozhet proniknut' cherez granicy konvektivnoi zony. Esli granica zhestkaya, to v silu deistviya vyazkosti na granicah i v_y = v_x = 0, a iz usloviya $\mathrm{div}\vec v = 0$ otsyuda sleduet ∂v_z/∂z = 0. Iz (5.116) togda nahodim i ∂(δT)/∂z = 0. No na svobodnyh granicah vozmozhny gorizontal'nye dvizheniya veshestva. Zdes' granichnye usloviya trebuyut obrasheniya v nul' kasatel'nyh natyazhenii, t. e. velichin ∂v_y/∂z + ∂v_z/∂y i ∂v_x/∂z + ∂v_z/∂x otkuda sleduet granichnoe uslovie ∂²v_z/∂t² = 0. My budem issledovat' sluchai, kogda kak nizhnyuyu, tak i verhnyuyu granicy konvektivnoi oblasti mozhno rassmatrivat' kak svobodnye poverhnosti, a poetomu primem, chto na obeih granicah

$\delta T = 0, \quad \frac{\partial^2}{\partial t^2}(\delta T) = 0.$ (5.120)

Vernemsya k uravneniyu (5.119) i budem iskat' ego reshenie v vide

$\frac{d^6\Theta}{dz^6} - 3k^2 \frac{d^4\Theta}{dz^4} + 3k^4 \frac{d^2\Theta}{dz^2} - k\Theta + \frac{g\alpha\beta}{\varkappa\nu}k^2\Theta = 0,$ (5.122)

gde k² = k_x² + k_y², pri sleduyushih granichnyh usloviyah:

$\left. \begin{array}{l} \Theta = 0 \\ \frac{d^2\Theta}{dz^2} = 0 \end{array} \right\} \mbox{pri } z=0, z=l.$ (5.123)

No iz uravneniya (5.122) srazu sleduet, chto pri usloviyah (5.123) na granicah ravny nulyu voobshe vse proizvodnye chetnogo poryadka, t e.

$\frac{d^{(2m)}\Theta}{dz^{(2m)}} = 0 \quad \mbox{pri } z=0, z=l.$ (5.124)

Eto oznachaet, chto resheniem uravnenii (5.122), (5.123) mozhet byt' tol'ko vyrazhenie

$\Theta = A\sin(n\pi z), \quad n=1,2,3,...\infty,$ (5.125)

gde A - proizvol'naya postoyannaya. Podstavim (5.125) v (5.122) i, oboznachaya

$a = kl,$ (5.126)

poluchim otsyuda

$R = \frac{g\alpha\beta}{\chi\nu}l^4 = \frac{(n^2\pi^2 + a^2)^3}{a^2}.$ (5.127)

Obsudim teper' poluchennoe reshenie. Ochevidno, chto naibol'shemu masshtabu dvizheniya sootvetstvuet sluchai n = 1. Pri n > 1 vertikal'naya komponenta skorosti obrashaet znak vnutri sloya, t. e. zdes' dvizheniya imeyut masshtab l/n. Primem poetomu n = 1. Dalee legko opredelit', chto (5.127) minimal'no, esli a = π/√2. Togda

$R_{min} = \frac{27}{4}\pi^4 = 657,5.$ (5.128)

Takim obrazom, laminarnaya konvekciya nastupaet togda, kogda sverhadiabaticheskii gradient budet bol'she, chem

$\beta \ge \frac{\chi\nu}{g\alpha l^4}\frac{27}{4}\pi^4.$ (5.129)

Zdes' poyavlyayutsya pravil'nye yacheiki s gorizontal'nym razmerom

$l_{\mbox{gor}} \approx \frac{2\pi}{k} = \frac{2\pi l}{kl} = 2\sqrt 2 l,$ (5.130)

t. e. primerno v tri raza bol'shim, chem tolshina konvektivnogo sloya. Esli uvelichivat' sverhadiabaticheskii temperaturnyi gradient, to uvelichivaetsya i chislo Releya. Pri etom rastet a, t. e. umen'shayutsya gorizontal'nye razmery yacheiki, a zatem uvelichivayutsya i n. Eto i oznachaet perehod k turbulentnoi konvekcii.

Vyshe my poluchili reshenie dlya sluchaya svobodnyh granic. Esli granicy zhestkie, chislo Releya bol'she i ravno 1700 [20]. Takim obrazom, tochnaya teoriya laminarnoi konvekcii podtverzhdaet opytnye dannye o tom, chto chislo Reinol'dsa dlya naimen'shih vihrevyh dvizhenii ne mozhet byt' slishkom malym; ono poryadka $\sqrt{R_{min}}$ ≈ 25.

Analogichnym obrazom reshaetsya zadacha o raschete chisla Releya dlya konvekcii s uchetom vrasheniya i magnitnyh polei. Podrobno eti problemy takzhe rassmotreny Chandrasekarom [20]. My privedem zdes' tol'ko nekotorye okonchatel'nye formuly.

Predpolozhim, chto konvektivnyi sloi vrashaetsya otnositel'no vertikal'nogo napravleniya s uglovoi skorost'yu Ω;;;. Togda poyavlyaetsya eshe odin razmernyi opredelyayushii parametr s razmernost'yu [Ω;;;] = sek^-1 i, sledovatel'no, eshe odin bezrazmernyi kompleks, kotoryi mozhno vybrat' v vide

$T = \frac{4\Omega^2}{\nu^2}l^4.$ (5.131)

Velichina T nazyvaetsya chislom Teilora. Ochevidno, chto mezhdu chislami Releya i Teilora sushestvuet svyaz', kotoruyu takzhe mozhno poluchit' iz obshih uravnenii dvizheniya. Okazalos' [20], chto

$R = \frac{1}{a^2}[(\pi^2 + a^2)^3 + \pi^2 T].$ (5.132)

Itak, vrashenie uvelichivaet chislo Releya, i, sledovatel'no, zatrudnyaet nastuplenie konvekcii. Esli uglovaya skorost' vrasheniya ochen' velika, t. e. esli T ≫ 1, to

$\begin{array}{l} a \to \left(\frac{1}{2}\pi^2 T\right)^{1/6} = 1,30T^{1/6}, \\ R \to 3\pi^4\left(\frac{T}{2\pi^4}\right)^{2/3} = 8,70T^{2/3}. \end{array}$ (5.133)

Harakter dvizheniya chastic gaza v konvekcii vo vrashayushemsya sloe izobrazhen na ris. 21. Chem bol'she T, tem bol'she zakruchivanie spiralei, t. e. tem men'she rasstoyanie mezhdu sosednimi vitkami.

Uchet vliyaniya magnitnogo polya vnosit eshe dva parametra: magnitnuyu indukciyu B i magnitnuyu vyazkost' ν_m. Razmernost' magnitnoi vyazkosti sovpadaet s razmernost'yu obychnoi vyazkosti i poetomu nezavisimym po razmernosti yavlyaetsya tol'ko parametr [B]= g ⋅ sm^1/2 ⋅ sek^-1.

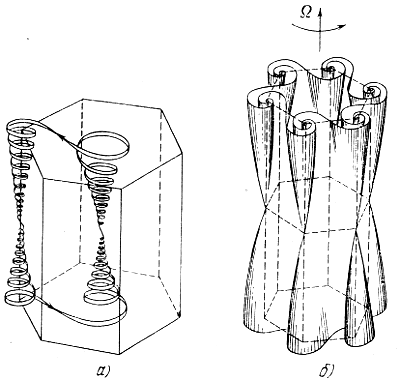
Ris. 21. Dvizhenie chastic (a) i struktura konvektivnyh shestiugol'nyh yacheek (b) v sluchae konvekcii v sloe neszhimaemoi zhidkosti, nahodyashemsya v bystrom vrashenii vokrug vertikal'noi osi (soglasno Chandrasekaru),

Poskol'ku poyavilas' razmernost' massy, vklyuchim v chislo opredelyayushih parametrov i plotnost' ρ , a tochnee, budem schitat' opredelyayushim parametrom kombinaciyu [B²/4πρ] = sm² ⋅ sek^-2. V rezul'tate obrazuetsya eshe odno bezrazmernoe chislo

$Q = \frac{B^2}{4\pi\rho\nu\nu_m},$ (5.134)

vvedennoe Chandrasekarom, no ostavsheesya bez nazvaniya.

Esli v konvektivnom sloe est' vertikal'noe magnitnoe pole, no net vrasheniya, to svyaz' mezhdu R i Q imeet vid

$R = \frac{\pi^2 + a^2}{a^2}[(\pi^2 + a^2) + \pi^2 Q].$ (5.135)

V ochen' sil'nyh magnitnyh polyah Q ≫ 1:

$a \to \left(\frac{1}{2}\pi^4 Q\right)^{1/6}, \quad R \to \pi^2 Q.$ (5.136)

Mozhno pokazat', chto gorizontal'noe magnitnoe pole ne vliyaet na konvekciyu, a sil'noe vertikal'noe pole, kak sleduet iz (5.136), zatrudnyaet nastuplenie konvekcii (rastet β) i privodit k tomu, chto konvektivnye elementy iz prizm so storonoi osnovaniya bol'she vysoty prevrashayutsya v tonkie stolby, kotorye v predele Q → ∞ stremyatsya k beskonechno tonkim nityam.

Sovmestnoe deistvie vrasheniya i magnitnogo polya privodit k sootnosheniyu

$R = \frac{(\pi^2 + a^2)\{[(\pi^2 + a^2) + \pi^2 Q]^2 + \pi^2(\pi^2 + a^2)T\}}{a^2[(\pi^2 + a^2) + \pi^2 Q]}$ (5.137)

Etot sluchai takzhe podrobno izuchen Chandrasekarom.

Nakonec, uchtem vliyanie prozrachnosti konvektivnyh elementov. Eto obobshenie na sluchai konvekcii bez magnitnogo polya bylo dano Shpigelem (sm. obzor [21]), a s uchetom vliyaniya magnitnogo polya - S. A. Kaplanom. Privedem osnovnye rezul'taty. Pust' τ_l est' opticheskaya tolsha vsego konvektivnogo sloya, t. e.

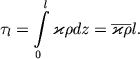
$\tau_l = \int\limits_0^l\varkappa\rho dz = \overline{\varkappa\rho}l.$ (5.138)

Togda, kak mozhno pokazat', uchet vozmozhnoi prozrachnosti konvektivnyh elementov privodit k zamene levoi chasti dlya chisla Releya (5.127) na velichinu

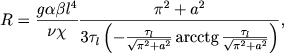
$R = \frac{g\alpha\beta l^4}{\nu\chi}\frac{\pi^2 + a^2}{3\tau_l\left(-\frac{\tau_l}{\sqrt{\pi^2 + a^2}} \arcctg\frac{\tau_l}{\sqrt{\pi^2 + a^2}} \right)},$ (5.139)

prichem pod χ teper' sleduet ponimat' luchistuyu temperaturoprovodnost', kotoraya svyazana s koefficientom neprozrachnosti ϰ sootnosheniem

$\chi = \frac{4\sigma T^3}{c_v\rho}\frac{c}{\varkappa\rho} \sim \frac{c}{\overline{\varkappa\rho}},$ (5.140)

gde c_v - teploemkost' pri postoyannom ob'eme, σ - postoyannaya zakona Stefana - Bol'cmana. Vtoroe sootnoshenie osnovano na predstavlenii, chto $1/\overline{\varkappa\rho}$ est' dlina svobodnogo probega kvanta, a s - ego skorost'.

Pravaya chast' R ravna lyubomu iz vyrazhenii (5.127), (5.132), (5.133), (5.135) - (5.137) v zavisimosti ot uslovii konvekcii. Iz opredeleniya (5.139) sleduet, chto v tom sluchae, kogda opticheskii razmer konvektivnogo elementa velik,

$\frac{\tau_l}{\sqrt{\pi^2 + a^2}} \gg 1,$ (5.141)

vtoroi mnozhitel' (5.139) blizok k edinice i konvekciya obladaet temi zhe svoistvami, chto p.v neprozrachnom sluchae. Odnako, esli imeet mesto obratnoe neravenstvo, kotoroe vozmozhno i pri bol'shoi opticheskoi tolshe sloya, t. e. τ_l ≫ 1 , esli tol'ko parametr a bol'shoi, a imenno, kogda

$\frac{\tau_l}{\sqrt{\pi^2 + a^2}} \approx \frac{\tau_l}{a} \ll 1,$ (5.142)

to vliyanie prozrachnosti sushestvenno. Zametim, chto velichina (5.142) est' opticheskii diametr konvektivnogo elementa. Yasno, chto esli etot element imeet vid tonkoi niti, kak v sluchae sil'nogo magnitnogo polya, to opticheskii diametr ϰρl/a mozhet byt' i men'she edinicy, hotya opticheskaya tolsha vsego konvektivnogo sloya $\overline{\varkappa\rho}l$ i mnogo bol'she edinicy.

V sluchae prozrachnoi konvekcii bez magnitnogo polya (t. e. pri priravnivanii (5.113) i (5.122)) i uslovii τ_l ≪ 1, poluchim

$a = \pi, \quad \frac{g\alpha\beta l^4}{\nu\chi} = 12\pi^2\tau_l.$ (5.143)

Zdes' konvektivnye elementy, po-prezhnemu, imeyut vid prizm, u kotoryh storona osnovaniya sravnima s vysotoi. Velichina sverhadiabaticheskogo gradienta okazyvaetsya mnogo men'she chem v neprozrachnom sloe (v $48\pi^2\tau_l^2/27$ raz).

Sil'noe vertikal'noe magnitnoe pole i zdes' vytyagivaet konvektivnye elementy. Q ≫ 1, to poluchim iz uslovii (5.139) i (5.135)

$a = (\pi^2 Q)^{1/4}.$ (5.144)

Uslovie prozrachnosti konvektivnyh elementov po diametru:

$\tau = \frac{\tau_l}{a} = \frac{\varkappa\rho l}{(\pi^2 Q)^{1/4}} \ll 1.$ (5.145)

Napomnim, chto opticheskaya tolsha vsego konvektivnogo sloya mozhet byt' i velika. Dlya sverhadiabaticheskogo gradienta takoi konvekcii budem imet':

$\frac{g\alpha\beta l^4}{\nu\chi} = 3\pi\tau^2_aQ^{1/2}$ (5.146)

ili, polagaya α = 1/T i $\chi = c/\overline{\varkappa\rho}$

$\beta = \frac{T}{d}\frac{3\pi c}{g}\frac{B}{\sqrt{4\pi\rho}}\left(\frac{\nu}{\nu_m}\right)^{1/2}\overline{\varkappa\rho}.$ (5.147)

Eto sootnoshenie spravedlivo tol'ko pri uslovii (5.145), t. e.

$\varkappa\rho(\nu\nu_m)^{1/4} \ll \left(\frac{\pi B}{d\sqrt{4\pi\rho}}\right)^{1/2}.$ (5.148)

Pri ochen' bol'shoi neprozrachnosti sloya i sil'nom magnitnom pole sverhadiabaticheskii gradient, soglasno (5.136),

$\beta = \frac{T}{d}\frac{\pi^2 c}{g}\frac{B^2}{\sqrt{4\pi\rho}}\frac{1}{\overline{\varkappa\rho}\nu_m l}.$ (5.149)

Uchet prozrachnosti konvektivnyh "nitei" pri sil'nom magnitnom pole oslablyaet podavlenie konvekcii magnitnym polem, v chastnosti, v prozrachnoi konvekcii β ∼ B, a v neprozrachnoi β ∼ B².

Dal'neishee obobshenie teorii svyazano s uchetom bolee bystrogo izmeneniya davleniya v konvektivnom sloe. Naprimer, esli schitat', chto davlenie v konvektivnom sloe padaet s vysotoi po barometricheskoi formule s ekvivalentnoi vysotoi N, to dlya chisla Releya poluchaetsya vyrazhenie [22]:

$R = \frac{\pi^2 + a^2 + (l/2H)^2}{a^2}\left[\left(\pi^2 + a^2 + \frac{l^2}{4H^2}\right)^2 - \frac{2}{3}\left(\frac{al}{H}\right)^2\right].$ (5.150)

Esli tolshina konvektivnogo sloya mnogo bol'she ekvivalentnoi vysoty (l ≫ H), to gorizontal'nyi razmer konvektivnyh yacheek i velichina sverhadiabaticheskogo gradienta opredelyayutsya tol'ko ekvivalentnoi vysotoi. Zdes'

$a \to 0,431\frac{l}{H}, \quad R \to 0,155 \left(\frac{l}{H}\right)^4,$ (5.151)

t. e. storona osnovaniya konvektivnyh prizm poryadka (2-3) N, a sverhadiabaticheskii gradient

$\beta = \frac{T}{H}0,155\frac{\nu\chi}{gH^3}.$ (5.152)

Vozmozhny i drugie obobsheniya.

Vyshe ochen' podrobno byl opisan sluchai laminarnoi konvekcii dlya sredy s odnorodnoi plotnost'yu Razumeetsya, s tochki zreniya astrofizicheskih primenenii teorii takoi sluchai yavlyaetsya daleko idushei idealizaciei. Naprimer, na Solnce konvekciya imeet mesto v sloe, plotnost' vnutri kotorogo menyaetsya na neskol'ko poryadkov velichin. Poetomu opisannaya vyshe teoriya k real'nym astrofizicheskim ob'ektam, strogo govorya, neprimenima. Tem ne menee i ona predstavlyaet dlya astrofiziki opredelennuyu cennost'. Vo-pervyh, harakternye chisla R, T, Q i τ_d polucheny iz soobrazhenii razmernosti i poetomu ih mozhno ispol'zovat' vo vseh sluchayah. Tochnye svyazi mezhdu etimi chislami zavisyat, konechno, ot idealizirovannoi postanovki zadachi, no kachestvennye harakteristiki i asimptoticheskoe povedenie imeyut bolee obshii harakter. Poetomu dlya ocenok effektov vliyaniya vrasheniya, magnitnogo polya, prozrachnosti vihrei na urovne konvekcii vsemi etimi sootnosheniyami vpolne mozhno pol'zovat'sya.

Vprochem, osnovnoi cel'yu stol' podrobnogo izlozheniya byla illyustraciya teh vozmozhnostei, kotorye daet teoriya analiza razmernostei i podobiya v etoi probleme.

Ved' vse poluchennye zdes' svyazi mezhdu bezrazmernymi kompleksami i est' sledstviya P-teoremy.

No vozvratimsya k real'noi astrofizicheskoi konvekcii. Kak uzhe bylo podrobno izlozheno v predydushei glave, konvekciya igraet ochen' bol'shuyu rol' v perenose energii v nedrah zvezd - v central'nyh konvektivnyh yadrah goryachih zvezd i v konvektivnyh zonah pod poverhnost'yu holodnyh zvezd. Zdes' konvekciya imeet preimushestvenno turbulentnyi harakter. Dostatochno udovletvoritel'noi teorii takoi konvekcii eshe net. Poetomu prihoditsya pribegat' k razlichnym polukachestvennym modelyam.

Mozhno ispol'zovat' i privedennye vyshe modeli stacionarnoi laminarnoi konvekcii, esli vmesto obychnoi vyazkosti podstavit' turbulentnuyu vyazkost'. Togda mozhno izuchit', naprimer, vliyanie magnitnyh polei i vrasheniya na velichinu sverhadiabaticheskogo gradienta. Velichina turbulentnoi vyazkosti podbiraetsya tak, chtoby chislo Reinol'dsa bylo by poryadka 30, a sledovatel'no, chislo Releya bez ucheta magnitnyh polei - okolo 10³.

Ochen' chasto ispol'zuetsya metod dliny peremeshivaniya. V etom metode zaranee zadaetsya vysota pod'ema konvektivnyh elementov l, nazyvaemaya dlinoi peremeshivaniya. Togda legko opredelit' skorost' pod'ema konvektivnogo elementa pod deistviem sily Arhimeda:

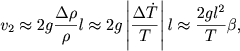
$v_2 \approx 2g\frac{\Delta\rho}{\rho}l \approx 2g\left|\frac{\Delta\dot T}{T}\right| l \approx \frac{2gl^2}{T}\beta,$ (5.153)

predpolagaya dvizhenie ravnouskorennym. Potok energii, perenosimyi konvekciei,

$F_{\mbox{konv}} \approx \rho c_p\delta T vl \approx \rho c_p vl\beta,$ (5.154)

gde c_p - teploemkost' pri postoyannom davlenii. Formula (5.154), v otlichie ot (5.91), opisyvaet potok teplovoi energii, perenosimoi konvekciei. K etim uravneniyam dobavlyaetsya takzhe uravnenie teploprovodnosti tipa (5.116), chto i pozvolyaet poluchit' sistemu uravnenii, opredelyayushih parametry konvektivnoi oblasti.

Pri raschetah zadaetsya F_konv i l. Velichina F_konv opredelyaetsya potokom energii, kotoryi dolzhen byt' perenesen v etoi zone, a velichinu l chasto vybirayut ravnoi ekvivalentnoi vysote sloya ili drugim parametram s razmernost'yu dliny.

Metod dliny peremeshivaniya dopuskaet tol'ko chislennoe reshenie. Bylo postroeno mnogo razlichnyh modelei, i v teorii vnutrennego stroeniya zvezd ili teorii konvektivnoi zony Solnca eti modeli igrayut ochen' bol'shuyu rol'. No s tochki zreniya teorii podobiya i analiza razmernostei eti modeli ne obsuzhdalis'. Eto trudno sdelat', poskol'ku zdes' net analiticheskih sootnoshenii.

Nakonec, v teorii turbulentnoi konvekcii ispol'zovalsya i metod postroeniya spektral'nyh uravnenii. Kak my uzhe otmechali, turbulentnost' opisyvaetsya spektral'noi funkciei W_k (sm. (5.87), (5.97), (5.107)). Mozhno popytat'sya srazu sostavit' uravneniya dlya etoi funkcii. Strogogo metoda polucheniya takih uravnenii net, no mozhno vospol'zovat'sya razlichnymi evristicheskimi soobrazheniyami, gde ne poslednyuyu rol' igrayut i soobrazheniya analiza razmernostei.

Naprimer, Ledu, Shvarcshil'd i Shpigel' [23] predlozhili sleduyushee integral'noe uravnenie dlya nahozhdeniya spektral'noi funkcii turbulentnoi konvekcii:

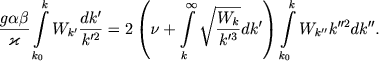
$\frac{g\alpha\beta}{\varkappa}\int\limits_{k_0}^k W_{k'}\frac{dk'}{k'^2} = 2\left(\nu + \int\limits_{k}^\infty \sqrt{\frac{W_k}{k'^3}} dk'\right) \int\limits_{k_0}^k W_{k^{\prime\prime}}k^{\prime\prime 2}dk^{\prime\prime}.$ (5.155)

Zdes' k₀ = 2π/l₀ - volnovoe chislo osnovnogo masshtaba konvektivnoi zony. V levoi chasti stoit velichina, opredelyayushaya silu vsplyvaniya, deistvuyushuyu na vse konvektivnye elementy s masshtabami bol'shimi, chem 2π/k. Pravaya chast' opredelyaet deistvie vyazkosti, v tom chisle i turbulentnoi, opisyvaemoi chlenom

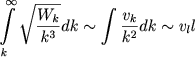
$\int\limits_{k}^\infty \sqrt{\frac{W_k}{k^3}} dk \sim \int\frac{v_k}{k^2}dk \sim v_l l$ (5.156)

soglasno predpolozheniyu Geizenberga.

V eto uravnenie mozhno vvesti i chleny, opisyvayushie deistvie magnitnogo polya na konvekciyu (sm. [17]).

Togda v pravoi chasti dobavitsya slagaemoe

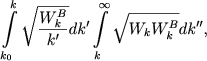
$\int\limits_{k_0}^k \sqrt{\frac{W_k^B}{k'}} dk' \int\limits_{k}^\infty\sqrt{W_k W_k^B}dk^{\prime\prime},$ (5.157)

gde $W_k^B$ - spektral'naya plotnost' magnitnoi energii, t. e. raspredelenie fluktuacii velichiny magnitnogo polya po raznym masshtabam. Takoi vid etogo chlena opredelyaetsya tem, chto pervyi mnozhitel' predstavlyaet soboi kak by "magnitnuyu vyazkost'" turbulentnogo dvizheniya. Razlichie mezhdu (5.156) i (5.157) zaklyuchaetsya v sleduyushem - turbulentnaya vyazkost' opredelyaetsya tem, chto melkomasshtabnye dvizheniya zabirayut energiyu ot krupnomasshtabnyh, a magnitnoe pole deistvuet naoborot - bolee sil'noe krupnomasshtabnoe pole podavlyaet dvizhenie melkomasshtabnyh polei. Vid vtorogo mnozhitelya opredelyaetsya soobrazheniyami analiza razmernostei i tem, chto magnitnaya sila vsegda proporcional'na $B^2 \sim W_k^B$ . Poskol'ku teper' est' dve neizvestnye spektral'nye funkcii, to sleduet zapisat' dva uravneniya vida (5.155). Vid vtorogo uravneniya zavisit ot togo, kak deistvuet arhimedova sila na magnitnoe pole. My seichas ne budem zanimat'sya obsuzhdeniem etogo metoda issledovaniya turbulentnoi konvekcii. Upomyanem tol'ko rezul'taty. V oblasti bol'shih masshtabov, sootvetstvuyushih tolshine konvektivnoi zony, spektral'naya funkciya

$W_k \sim k^{-7},$ (5.158)

chemu sootvetstvuet sootnoshenie $v_l \sim l^3$ . Eto oznachaet, chto pochti vsya energiya dvizheniya sosredotochena v oblasti samyh krupnyh masshtabov, chto kachestvenno sootvetstvuet opisannoi vyshe kartine laminarnoi konvekcii. V oblasti men'shih masshtabov, no bez ucheta magnitnogo polya,

$W_k \sim k^{5/3}, \quad v_l \sim l^{1/3},$ (5.159)

t. e. poyavilsya spektr Kolmogorova. Eta oblast' masshtabov opredelyaet turbulentnuyu vyazkost'. Nakonec, v toi oblasti spektra, gde sil'no vliyanie magnitnogo polya

$W_k^B \sim W_k \sim k^{-2}, \quad v_l \sim l^{1/2}.$ (5.160)

Zdes' spektr bolee krutoi, chem bez ucheta magnitnogo polya.

K sozhaleniyu, vse eti metody imeyut tot sushestvennyi nedostatok, chto, poskol'ku sami uravneniya sostavlyayutsya s izvestnoi dolei proizvola, to i resheniya ne imeyut sily dokazatel'stv. V luchshem sluchae ih mozhno rassmatrivat' tol'ko kak kachestvennuyu harakteristiku yavleniya.

Mozhno postroit' bolee stroguyu teoriyu, dlya konvekcii v ochen' sil'nom magnitnom pole. Zdes' gaz uzhe ne mozhet svobodno dvigat'sya po konvektivnoi oblasti i konvekciya stanovitsya kolebatel'noi. Model' takoi konvekcii rassmotrel Yu. D. Zhugzhda [24]. Esli imeetsya gradient temperatury vdol' magnitnyh silovyh linii, to teplovaya energiya mozhet perenosit'sya i pri kolebaniyah gaza v takom sil'nom magnitnom pole. Zadachu mozhno rassmotret' strogo, no prostyh analiticheskih sootnoshenii poluchit' ne udalos'. Eta teoriya pozvolila ob'yasnit' slozhnuyu strukturu teni i poluteni solnechnyh pyaten, a takzhe i nekotorye drugie yavleniya solnechnoi aktivnosti (sm. obzor [25]). Konvekciya v politropnoi atmosfere s magnitnym polem izuchalas' v rabote [26]. Zdes' takzhe udalos' poluchit' zavisimost' sverhadiabaticheskogo gradienta temperatury ot napryazhennosti magnitnogo polya.

V zaklyuchenie eshe raz podcherknem, chto v teorii turbulentnosti i teorii konvekcii metody analiza razmernostei i teorii podobiya okazalis' ves'ma effektivnymi, no, k sozhaleniyu, my eshe daleki ot sozdaniya takoi teorii, kotoraya udovletvoritel'no opisyvala by astrofizicheskie usloviya.

<< § 5.2 Vrashenie i magnitnye polya zvezd | Oglavlenie | § 5.4 Cirkulyaciya v atmosferah planet >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce