po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 5.4 Cirkulyaciya v atmosferah planet | Oglavlenie | § 6.2 Ionizacionnye fronty i udarnye volny vysvechivaniya v mezhzvezdnom prostranstve >>

Glava VI. Avtomodel'nye dvizheniya v zvezdah i mezhzvezdnom prostranstve

Issledovanie dvizheniya gaza v kosmicheskih usloviyah predstavlyaet soboi vazhnyi razdel sovremennoi astrofiziki. Mozhno ukazat' mnogo problem astrofiziki, kosmogonii, kosmologii i t. d., trebuyushih rascheta harakteristik dvizheniya gaza. Problema obrazovaniya zvezd, galaktik, skoplenii galaktik trebuet resheniya zadachi o kollapse gazovoi massy pod vliyaniem gravitacionnogo prityazheniya. Teoriya evolyucii zvezd, v chastnosti, poyavlenie vspyshek novyh i sverhnovyh, trebuet izucheniya obrazovaniya i dvizheniya udarnyh voln v zvezdah. Issledovanie tesnyh dvoinyh sistem potrebovalo rassmotreniya peretekaniya gazovyh potokov ot odnoi zvezdy k drugoi. Takih primerov mozhno ukazat' mnogo.

Vse eto privelo k tomu, chto voznikla novaya oblast' astrofiziki - kosmicheskaya gazodinamika (v tom chisle i ee razdel - mezhzvezdnaya gazodinamika). Uzhe poyavilos' mnogo obobshayushih issledovanii i knig po etoi probleme, neodnokratno sozyvalis' konferencii (sm. [1-6]).

Kosmicheskaya gazodinamika shiroko ispol'zuet metody teorii analiza razmernostei i podobiya. V etoi glave my rassmotrim lish' te zadachi kosmicheskoi gazodinamiki, gde eti metody yavlyayutsya osnovnymi. V silu obshirnosti problemy i ogranichennosti mesta my ne mozhem obsudit' vse zadachi kosmicheskoi gazodinamiki, kotorye mogut byt' rassmotreny metodami teorii analiza razmernostei i podobiya, i ogranichimsya poetomu lish' nekotorymi iz nih, kotorye po tem ili inym prichinam pokazalis' nam naibolee interesnymi.

Vazhno takzhe otmetit', chto primenenie metodov teorii analiza razmernostei i podobiya k nekotorym problemam kosmicheskoi gazodinamiki bylo dano takzhe v knigah L. I. Sedova [7] i K. P. Stanyukovicha [8], gde chitatel' mozhet naiti bol'she podrobnostei matematicheskogo analiza etih problem.

§ 6.1 Uravneniya avtomodel'nogo dvizheniya kosmicheskogo gaza

Ochen' prostym yavlyaetsya sluchai avtomodel'nogo (ili samopodobnogo) dvizheniya gaza. Zdes' mozhno iz soobrazhenii razmernosti poluchit' obshie harakteristiki dvizheniya, ne pribegaya k resheniyu slozhnyh uravnenii dvizheniya. S drugoi storony, rassmatrivaya avtomodel'nye dvizheniya, mozhno svesti gazodinamicheskie uravneniya v chastnyh proizvodnyh k sistemam bolee prostyh uravnenii v obyknovennyh proizvodnyh, dlya kotoryh k tomu zhe mogut byt' srazu opredeleny integraly dvizheniya. Avtomodel'nye dvizheniya, metody ih issledovaniya, sootvetstvuyushie sistemy obyknovennyh uravnenii i metody ih analiza podrobno izlozheny v knige L. I. Sedova [7] i poetomu ogranichimsya lish' nekotorym obshim obsuzhdeniem primenenii metoda avtomodel'nyh dvizhenii k problemam astrofiziki, a v posleduyushih paragrafah rassmotrim nekotorye konkretnye zadachi, ne zatronutye v [7, 8].

Kak eto chasto byvaet v fizike, naibolee prostymi s tochki zreniya teoreticheskogo analiza yavlyayutsya odnomernye dvizheniya - ploskie, cilindricheski- ili sfericheski-simmetrichnye. Pravda, metodami teorii avtomodel'nyh dvizhenii mozhno rassmotret' i bolee slozhnuyu geometriyu, naprimer, ne tol'ko cilindricheski-simmetrichnyi sluchai, no takzhe i dvizhenie s aksial'noi simmetriei. Odnako my zdes' ogranichimsya sluchaem odnomernyh dvizhenii.

Deistvitel'no, nesmotrya na slozhnost' dvizhenii v kosmicheskih usloviyah, real'naya geometriya v bol'shinstve astrofizicheskih zadach vse ravno ne mozhet byt' uchtena v ramkah toi tochnosti teorii i nablyudenii, kotoraya nam dostupna v nastoyashee vremya. Poetomu predpolozhenie o nekotoroi odnomernoi simmetrii dvizhenii ne ochen' meshaet obshnosti vyvodov i v to zhe vremya sushestvenno uproshaet matematicheskii analiz.

K tomu zhe avtomodel'nost' dvizheniya imeet mesto tol'ko togda, kogda eto dvizhenie harakterizuetsya ne bolee, chem dvumya opredelyayushimi parametrami s nezavisimymi razmernostyami. Poyasnim, chto eto znachit. Dvizhenie gaza opredelyaetsya kakimi-to vneshnimi ili vnutrennimi prichinami. Naprimer, ono mozhet byt' svyazano s nagrevaniem gaza izlucheniem - togda opredelyayushim parametrom yavlyaetsya potok luchistoi energii. Dvizhenie mozhet byt' vyzvano vnezapnym osvobozhdeniem bol'shogo kolichestva energii - vzryvom. Moshnost' vzryva togda tozhe yavlyaetsya opredelyayushim parametrom. Est' opredelyayushie parametry, harakterizuyushie nachal'noe sostoyanie gaza, naprimer, ego plotnost' i davlenie.

Estestvenno, chto dvizhenie kosmicheskogo gaza harakterizuetsya mnogimi opredelyayushimi parametrami. No chasto mozhno vydelit' dva osnovnyh, glavnyh parametra s nezavisimymi razmernostyami, kotorye opredelyayut osnovnye svoistva dvizheniya - v etom sluchae zadacha stanovitsya avtomodel'noi i ee mozhno issledovat' otnositel'no prosto. Oboznachim eti dva osnovnyh opredelyayushih parametra cherez A i V i, ne ogranichivaya obshnosti, mozhem prinyat' dlya ih razmernostei (sm. [7]):

$[A] = \mbox{g} \cdot (\mbox{sm})^{k_1} \cdot (\mbox{sek})^{k_2}, \quad [B] = (\mbox{sm})^{k_3} \cdot (\mbox{sek})^{k_4},$ (6.1)

gde k₁, k₂, k₃, k₄ - nekotorye racional'nye chisla, kotorye mogut byt' i ne celymi. Simmetrichnoe odnomernoe dvizhenie harakterizuetsya koordinatoi r i vremenem t. Iz chetyreh razmernyh velichin sostavlyaetsya odna bezrazmernaya kombinaciya, kotoruyu my zapishem v vide

$\lambda = B^{-1/k_4}rt^{k_3/k_4} = \frac{r}{B^{-1/k_4}t^\delta},$ (6.2)

gde δ = -k₃/k₄.

Drugie bezrazmernye kompleksy obrazuem iz parametrov A, V i harakteristik dvizheniya i sostoyaniya gaza: skorosti v, plotnosti ρ i davleniya r, a takzhe koordinaty r. Sostavlyaya matricu razmernosti s etimi parametrami, nahodim tri bezrazmernyh kompleksa:

$\Pi_1 = \frac{vr^{1/\delta - 1}}{B^{1/\delta}}, \quad \Pi_2 = \frac{\rho r^{k_1+ 3+k_2/\delta}}{AB^{k_2/\delta k_4}}, \quad \Pi_3 = \frac{pr^{k+1+(k_2+2)/\delta}}{AB^{(k_2+2)/\delta k_4}}.$ (6.3)

Znachenie etih kompleksov my obsudim nizhe.

Nakonec, privedem sami uravneniya avtomodel'nogo dvizheniya. Dlya etogo zapishem uravneniya simmetrichnogo dvizheniya politropnogo gaza v prosteishem sluchae, kogda mozhno prenebrech' gravitaciei, magnitnymi polyami i dissipativnymi effektami [7]:

$\frac{\partial v}{\partial t} + v\frac{\partial v}{\partial r} + \frac{1}{\rho}\frac{\partial p}{\partial r} = 0,$ (6.4)

$\frac{\partial \rho}{\partial t} + \frac{\partial}{\partial r}(\rho v) + (\nu - 1)\frac{\rho v}{r} = 0,$ (6.5)

$\frac{\partial}{\partial t}\left(\frac{p}{\rho^\gamma}\right) + v \frac{\partial}{\partial r}\left(\frac{p}{\rho^\gamma}\right) = 0.$ (6.6)

Zdes' γ - pokazatel' politropnogo sostoyaniya, indeks ν harakterizuet simmetriyu dvizheniya: ν = 1 dlya ploskih, ν = 2 dlya cilindricheski-simmetrichnyh i ν = 3 dlya sfericheski-simmetrichnyh dvizhenii. Zametim, chto sistema (6.4) - (6.6) vklyuchaet kak chastnyi sluchai i vazhnye dlya astrofiziki izotermicheskie dvizheniya [5], gde γ = 1.

Teper' pereidem v (6.4) - (6.6) k bezrazmernym funkciyam odnogo argumenta λ po formulam

$v = \frac{r}{t}V(\lambda), \quad \rho = \frac{A}{r^{k_1 + 3}t^{k_2}}R(\lambda), \quad p = \frac{A}{r^{k_1 + 1}t^{k_2 + 2}}P(\lambda);$ (6.7)

togda poluchitsya sistema treh uravnenii v obyknovennyh proizvodnyh po λ dlya funkcii V(λ), R(λ) i R(λ). My etu sistemu zapisyvat' ne budem, a srazu privedem ee v preobrazovannom vide, naibolee udobnom dlya resheniya:

$\begin{array}{ll} \frac{dZ}{dV} = &\frac{Z\{[2(V-1) + \nu(\gamma - 1)V](V-\delta)^2 - (\gamma - 1)V(V-1)(V-\delta)\}}{(V-\delta)[V(V-1)(V-\delta) + (\varkappa - \nu V)Z]} - \\ &-\frac{Z^2[2(V-1) + \varkappa(\gamma - 1)]}{(V-\delta)[V(V-1)(V-\delta) + (\varkappa - \nu V)Z]}, \end{array}$ (6.8)

$\begin{array}{l} (V-\delta)\frac{d\ln R}{d\ln\lambda} = \\ = [k_2 + (k_1 - \nu + 3)V] - \frac{V(V-1)(V-\delta) + (\varkappa - \nu V)Z}{Z - (V-\delta)^2}, \end{array}$ (6.9)

$\frac{d\ln \lambda}{dV} = \frac{Z - (V-\delta)^2}{V(V-1)(V-\delta) + (\varkappa - \nu V)Z},$ (6.10)

gde

$\varkappa = \frac{k_2 + 2 + \delta(k_1 + 1)}{\gamma},$ (6.11)

a novaya bezrazmernaya funkciya

$Z(\lambda) = \gamma\frac{P(\lambda)}{R(\lambda)}$ (6.12)

est' kvadrat bezrazmernoi skorosti zvuka (ili bezrazmernoi temperatury).

My vypisali sistemu uravnenii (6.8) - (6.12) vo vseh detalyah, poskol'ku v dal'neishem budet rassmatrivat'sya ee reshenie dlya nekotoryh chastnyh sluchaev. Kak uzhe otmechalos', sistema uravnenii (6.8) - (6.12) poluchena i podrobno issledovana v naibolee obshem vide L. I. Sedovym [7].

Srazu vidno, chto, po sushestvu, zdes' nado naiti reshenie odnogo uravneniya (6.8), t.e. naiti zavisimost' Z ot V. Posle etogo uravneniya (6.9) i (6.10) svodyatsya k kvadraturam. Eto osobenno prosto sdelat' dlya izotermicheskogo dvizheniya (γ = 1), kotoroe budet podrobno issledovano v sleduyushem paragrafe.

Teper' my mozhem vernut'sya k obshemu obsuzhdeniyu svoistv avtomodel'nogo dvizheniya. Sistema (6.8) - (6.12) opredelyaet odnoznachnuyu zavisimost' bezrazmernyh parametrov dvizheniya R, R, V i Z ot λ . Pust' v nekotoryi moment vremeni t = t₁ imeetsya opredelennoe raspredelenie etih parametrov v prostranstve, t. e. zavisimost' ot koordinaty r (a sledovatel'no, i ot parametra λ (6.2)). V drugoi moment vremeni t = t₁ eto raspredelenie budet drugim, no podobnym pervomu, poskol'ku zavisimost' ot λ ostalas' neizmennoi. Uslovie podobiya (ili avtomodel'nosti) mozhet byt' zapisano kak λ = const ili

$Z(\lambda) = \gamma\frac{P(\lambda)}{R(\lambda)}$ (6.13)

Takim obrazom, reshiv sistemu (6.8) - (6.12) pri sootvetstvuyushih granichnyh usloviyah, my poluchaem polnuyu kartinu dvizheniya gaza i raspredelenie kak v prostranstve, tak i vo vremeni velichin, harakterizuyushih eto dvizhenie (skorosti, plotnosti i t.p.). Dvizhenie ostaetsya podobnym samomu sebe i poetomu osobenno udobno prosledit' za peremesheniem kakoi-libo ekstremal'noi harakteristiki.

Naprimer, kak horosho izvestno, pri dvizhenii gaza chasto voznikayut razryvy - skachki plotnosti, skorosti, temperatury ili ionizacionnye razryvy v mezhzvezdnom prostranstve. Na takih skachkah terpyat razryvy i bezrazmernye funkcii R(λ), R(λ), V(λ) i Z(λ). Ochevidno, chto dlya sohraneniya avtomodel'nosti dvizheniya kazhdyi razryv dolzhen harakterizovat'sya opredelennym znacheniem parametra λ . Takim obrazom, my srazu poluchaem zakon peremesheniya lyubogo razryva v avtomodel'nom dvizhenii

$r_s = \lambda_s B^{1/k_4}t^\delta ,$ (6.14)

gde λ_s = const. Velichina Xs mozhet byt' opredelena pri polnom reshenii uravnenii (6.8) - (6.12). No dazhe i bez tochnogo chislennogo opredeleniya velichiny Xs odno uslovie λ_s = const daet vozmozhnost' izuchit' zavisimost' polozheniya fronta razryva ot vremeni. Sobstvenno, dlya astrofizicheskih primenenii znanie tochnogo znacheniya λ_s chasto i ne nuzhno voobshe, poskol'ku chislennye znacheniya opredelyayushih parametrov izvestny lish' priblizhenno, inogda dazhe s tochnost'yu do poryadka velichiny. V etih sluchayah mozhno prinyat' λ_s=1. No v drugih sluchayah vychislenie λ_s. neobhodimo. Takoi sluchai, v chastnosti, vazhen dlya rascheta dvizheniya ionizacionnyh razryvov v mezhzvezdnom prostranstve (sm. sleduyushii paragraf). Podrobno metody vychisleniya skachkov parametrov i uchet ih v ramkah teorii avtomodel'nogo dvizheniya takzhe izlozheny v [7].

Odnim iz pervyh uspehov teorii avtomodel'nogo dvizheniya bylo reshenie zadachi o sil'nom vzryve. Eto reshenie, poluchennoe L. I. Sedovym v 1945 g. i ispol'zovannoe im dlya rascheta rasshireniya ognennogo shara atomnogo vzryva, bylo zatem primeneno I. S. Shklovskim (sm. [9]) k analizu dvizheniya obolochki sverhnovoi II tipa v mezhzvezdnoi srede. Rassmotrim etot sluchai podrobnee.

Pust' v odnorodnoi po plotnosti mezhzvezdnoi srede raspolozhena zvezda, kotoraya v nachal'nyi moment t=0 vspyhivaet kak sverhnovaya. Ona sbrasyvaet obolochku, imeyushuyu nekotoruyu kineticheskuyu energiyu (s razmernost'yu erg = g ⋅ sm² ⋅ sek^-2). Budem schitat', chto eta obolochka sfericheski-simmetrichna. Rasshiryayas', obolochka sverhnovoi vovlekaet v dvizhenie mezhzvezdnyi gaz, peredavaya emu svoyu energiyu. Skorost' obolochki sverhnovoi na nachal'nom etape poryadka 3-6 tysyach km/sek, t. e. bol'she skorosti zvuka. Mezhzvezdnyi gaz, vovlekaemyi v dvizhenie, tormozit obolochku, no eshe dolgo skorost' gaza ostaetsya sverhzvukovoi. Eto oznachaet, chto perednii front oblasti dvizheniya gaza predstavlyaet soboi udarnuyu volnu, na kotoroi imeet mesto skachok plotnosti, temperatury i skorosti.

Voobshe govorya, harakter dvizheniya sushestvenno zavisit ot usloviya poter' energii gaza na izluchenie. Mezhzvezdnyi gaz, uvlekaemyi obolochkoi sverhnovoi, nagrevaetsya i poetomu izluchaet energiyu. Raschety pokazyvayut, chto osobenno intensivno eto izluchenie pri temperature gaza okolo 10⁵ gradusov. Pri bolee nizkih temperaturah mala moshnost' mehanizmov teplovogo izlucheniya gaza, a pri bolee vysokih temperaturah vodorod i gelii uzhe ionizovany i effektivnost' poter' energii opyat' umen'shaetsya. Pri temperaturah poryadka 10⁵ gradusov izluchayutsya ul'trafioletovye spektry osnovnyh elementov.

Dopustim teper', chto na perednem fronte dvizhusheisya oblasti mezhzvezdnogo gaza skachok temperatury nastol'ko velik, chto za etim frontom temperatura podnimaetsya mnogo vyshe 10⁵ gradusov. Togda izluchenie nagretogo gaza otnositel'no neveliko i mozhno schitat', chto pri dvizhenii mezhzvezdnogo gaza i obolochki sverhnovoi sohranyaetsya polnaya energiya vzryva E, raspredelennaya teper' mezhdu kineticheskoi energiei vovlechennogo v dvizhenie mezhzvezdnogo gaza i ego teplovoi energiei. Itak, odin iz opredelyayushih parametrov est' polnaya energiya E, vydelivshayasya pri vspyshke sverhnovoi.

Ostaetsya vybrat' eshe odin parametr. Ochevidno, im mozhet byt' tol'ko plotnost' nevozmushennogo mezhzvezdnogo gaza ρ . Davleniem nevozmushennogo mezhzvezdnogo gaza, a sledovatel'no, i ego temperaturoi pridetsya prenebrech'. Eto mozhno sdelat', poskol'ku, po usloviyu, temperatura za frontom mnogo bol'she 10⁵ gradusov, a temperatura mezhzvezdnogo gaza deistvitel'no mnogo men'she etoi velichiny. Uchet "protivodavleniya" (t. e. davleniya gaza pered frontom rasshiryayusheisya oblasti) lishaet rassmatrivaemuyu zadachu usloviya avtomodel'nosti. Teoriya sil'nogo vzryva s uchetom protivodavleniya podrobno rassmotrena v knigah [7] i [10]. K astrofizicheskim zadacham eta teoriya poka eshe ne primenyalas'.

Itak, poka temperatura gaza, vovlechennogo v dvizhenie, velika, zadacha o dvizhenii obolochki sverhnovoi zvezdy v mezhzvezdnoi srede imeet dva opredelyayushih parametra, kotorye my vyberem tak:

$[\rho] = \mbox{g} \cdot \mbox{sm}^{-3}, \quad \left[\frac{E}{\rho}\right] = \mbox{sm}^{5} \cdot \mbox{sek}^{-2}.$ (6.15)

Sravnivaya s izlozhennymi vyshe sootnosheniyami, my mozhem prinyat' A = ρ, t. e. k₁ = -3 i k₂ = 0, i V = E/ρ, t. e. k₃ = 5, k₄ = -2 i δ = 2/5.

Iz (6.15) srazu sleduet uravnenie rasprostraneniya perednego fronta oblasti mezhzvezdnogo gaza, szhatogo obolochkoi sverhnovoi:

$r_{\mbox{ud}} \approx \left(\frac{E}{\rho}\right)^{1/5}t^{2/5},$ (6.16)

gde dlya prostoty postoyannaya velichina λ_s , prinyata ravnoi edinice. Togda E - eto energiya vspyshki sverhnovoi s tochnost'yu do nekotorogo chislennogo mnozhitelya poryadka edinicy (dlya sluchaya sil'nogo vzryva v vozduhe etot mnozhitel' raven 0,85 [7]).

Skorost' dvizheniya fronta etoi oblasti

$v_{\mbox{ud}} = \frac{dr}{dt} = \frac{2}{5}\left(\frac{E}{\rho}\right)^{1/5}t^{-3/5} = \frac{2}{5}\left(\frac{E}{\rho}\right)^{1/2} r_{\mbox{ud}}^{-3/2}.$ (6.17)

K sozhaleniyu, my ne mozhem prosledit' za izmeneniem skorosti dvizheniya obolochki odnoi i toi zhe sverhnovoi s techeniem vremeni ili s uvelicheniem ee rasstoyaniya ot centra iz-za "nedostatka" vremeni. No mozhno proverit' primenimost' sootnosheniya (6.17) statisticheskim metodom.

Dlya primera privedem grafiki T. A. Lozinskoi [11], na kotoryh dlya ryada tumannostei - ostatkov sverhnovyh - naneseny zavisimosti velichin $v_{\mbox{ud}}\rho^{1/5} \sim v_{\mbox{ud}} n^{1/5}_e$ kak ot vremeni t (ris. 22, a), tak i ot velichiny $r_{\mbox{ud}}\rho^{-3/5} \sim rn^{-3/5}_e$ (ris. 22, b). Esli by vse vspyshki sverhnovyh byli svyazany s osvobozhdeniem odnoi i toi zhe energii E, to soglasno (6.17) vse harakternye tochki okazalis' by na odnoi pryamoi v sootvetstvii s usloviem v_udρ^1/5t^3/5 = const ili $v_{\mbox{ud}}\rho^{1/2}r_{\mbox{ud}}^{3/2}$ = const. Estestvenno, chto imeetsya razbros velichiny E, no iz etih grafikov vidno, chto vse zhe sushestvuet opredelennaya koncentraciya k dvum pryamym. Nalichie dvuh pryamyh otrazhaet sushestvovanie dvuh tipov sverhnovyh s razlichnym harakterom vzryvov. Harakternye velichiny energii vspyshek sleduyushie: dlya bolee moshnyh sverhnovyh (tak nazyvaemyh sverhnovyh II tipa, dayushih tumannosti vida Petli v Lebede ili istochnika Kassiopeya A) velichina E ≈ 10⁵¹ erg; u bolee slabyh sverhnovyh I tipa (davshei, naprimer, Krabovidnuyu tumannost') E ≈ 10⁴⁸ erg.

Eti ocenki takzhe poluchayutsya iz formuly (6.17), esli ee primenit' dlya otdel'nyh tumannostei s izvestnymi parametrami. Naprimer, dlya tumannosti Petlya v Lebede imeem v_ud ≈ 100 km ⋅ sek^-1, ρ = 10^-23 g ⋅ sm^-3, r_ud = 20 ps, otkuda i nahodim E ≈ 10⁵¹ erg. Kstati, etu zhe formulu mozhno ispol'zovat' i dlya ocenki vremeni sushestvovaniya tumannosti. Poluchaem t ≈ 3 ⋅ 10⁴ let.

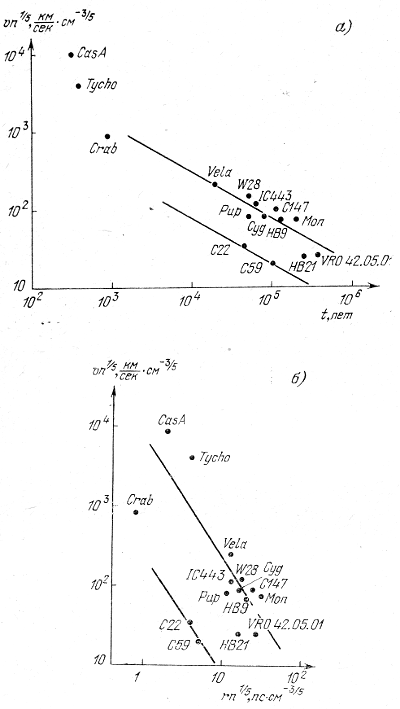
Ris. 22. Zavisimost' skorosti rasshireniya obolochki sverhnovyh ot vremeni (a) i ot razmera tumannosti - ostatka sverhnovoi (b) (soglasno T. A. Lozinskoi).

Teoriya sil'nogo vzryva mozhet ob'yasnit' i krivye bleska novyh (sm. [12]). Kak pokazyvayut nablyudeniya, posle maksimuma bleska svetimost' novoi padaet kak L ∼ t^-1. S drugoi storony, my znaem, chto svetimost' obolochki novoi proporcional'na ee ob'emu (t. e. r_ud³) i kvadratu koncentracii elektronov, t. e. ρ². Esli predpolozhit', chto massa obolochki novoi sohranyaetsya (poka net zametnogo "nagrebaniya" mezhzvezdnoi sredy), to mozhno prinyat' ρ ∼ r_ud^-3 , otkuda iz sootnosheniya (6.16) L ∼ ρ²r_ud³ ∼ r_ud^-3 ∼ t^-6/5, chto bolee ili menee soglasuetsya s nablyudaemoi zavisimost'yu.

Zametim, chto pri cilindricheskom i lineinom razlete obolochki svetimost' padala by znachitel'no medlennee, kak L ∼ t^-4/5 i L ∼ t^-2/5 sootvetstvenno. Poetomu obrazovanie volokon na bolee pozdnei stadii rasshireniya blagopriyatstvuet bolee dlitel'nomu sohraneniyu svecheniya; v etom, vozmozhno, i zaklyuchaetsya otvet na izvestnyi vopros G. A. Shaina - pochemu na nebe tak mnogo voloknistyh tumannostei?

Vernemsya k analizu avtomodel'noi zadachi. Reshenie uravnenii (6.8) - (6.12) dlya dannogo sluchaya pozvolyaet opredelit' raspredelenie temperatury i plotnosti za perednim frontom dvizhushegosya gaza. Tochnye resheniya dlya raznyh znachenii γ privedeny v [7]. My zdes' opishem ih tol'ko kachestvenno. Na fronte udarnoi volny dvizhushegosya gaza plotnost' skachkom vozrastaet do velichiny ρ₂, gde

$\frac{\rho_2}{\rho} = \frac{\gamma + 1}{\gamma -1}$ (6.18)

(pri γ = 5/3 - v chetyre raza). Temperatura gaza ravna

$T_2 = \frac{\mu}{\Re}\frac{2(\gamma - 1)}{(\gamma + 1)^2} v^2_{\mbox{ud}} = \frac{3}{100}\frac{\mu}{\Re}\frac{E}{\rho r_{\mbox{ud}}^3},$ (6.19)

gde μ molekulyarnyi ves, ℜ - universal'naya gazovaya postoyannaya, v_ud skorost' udarnoi volny. Vo vtorom ravenstve prinyato γ = 5/3 i ispol'zovana vtoraya formula (6.17). Srazu zhe za frontom udarnoi volny plotnost' gaza bystro spadaet, a temperatura rastet eshe bol'she, tak chto davlenie gaza snachala neskol'ko umen'shaetsya (primerno v dva raza), a potom ostaetsya postoyannym po vsei vnutrennei oblasti, ohvachennoi dvizheniem.

Poskol'ku intensivnost' izlucheniya nagretogo gaza pri T ≈ 10⁵ gradusov spadaet kak s umen'sheniem plotnosti, tak i s uvelicheniem temperatury, to eto oznachaet, chto elektromagnitnoe izluchenie (preimushestvenno v rentgenovskom i ul'trafioletovom diapazonah) generiruetsya tol'ko v ochen' uzkom sloe, prilegayushem k perednemu frontu dvizhushegosya gaza. Veroyatno, otnositel'naya tolshina izluchayushei oblasti poryadka 1/10 radiusa perednego fronta.

Po mere rasshireniya oblasti dvizhushegosya mezhzvezdnogo gaza temperatura T₂ padaet, i kogda ona okazhetsya men'shei 10⁵ gradusov, izluchenie stanet ves'ma effektivnym. Zdes' uzhe znachitel'naya - chast' energii teryaetsya na izluchenie i my ne mozhem bol'she schitat' polnuyu energiyu E sohranyayushimsya, a sledovatel'no, i opredelyayushim parametrom.

No ne tol'ko poteri energii na izluchenie ogranichivayut primenimost' etogo resheniya. Delo v tom, chto zdes' predpolagaetsya, chto udarnaya volna v mezhzvezdnoi srede obrazuetsya srazu zhe posle vzryva i nachala dvizheniya obolochki sverhnovoi. Na samom dele eto ne tak, poskol'ku v real'noi mezhzvezdnoi srede opredelennuyu rol' igrayut razlichnye dissipativnye koefficienty i obrazovanie udarnoi volny proishodit lish' cherez nekotoroe vremya posle nachala dvizheniya obolochki.

V rabote V. F. D'yachenko, V. S. Imshennika i V. V. Paleichika [13] bylo polucheno chislennoe reshenie sleduyushei zadachi. V vodorodnoi polnost'yu ionizovannoi plazme v nekotoryi moment vremeni nachinaet dvigat'sya s postoyannoi skorost'yu sfericheskii porshen'. Reshalas' sistema uravnenii, opisyvayushaya kak ionnuyu, tak i elektronnuyu komponentu plazmy s uchetom besstolknovitel'nyh processov, vyazkosti i teploprovodnosti oboih komponent i obmena energiei mezhdu nami.

Nachal'naya stadiya dvizheniya obolochki ne imeet gazodinamicheskogo haraktera i udarnaya volna obrazuetsya lish' cherez nekotoroe vremya, opredelennoe vyazkost'yu protonnoi komponenty plazmy. Kak bylo pokazano v rabote [13], udarnaya volna obrazuetsya cherez vremya t₀ posle vzryva, gde

$t_0 \approx (0,3-0,5)\frac{m_p^3}{e^4\Lambda}\frac{v_0^3}{\rho} \approx 10^{-35}\frac{v_0^3}{\rho}\mbox{sek}.$ (6.20)

Zdes' v₀ - nachal'naya skorost' obolochki, m_p i e - massa i zaryad protonov, Λ ≈ 30-70 - kulonovskii logarifm.

Nachal'nye skorosti obolochek sverhnovyh mogut dostigat' znacheniya ∼ 5 ⋅ 10³ km/sek. Pri plotnosti mezhzvezdnoi sredy ρ ≈ 10^-23 g/sm³ mozhno poluchit' iz (6.20) ocenku vremeni obrazovaniya udarnoi volny ∼ 3 ⋅ 10⁶ let. Mozhno postavit' vopros inache - kakaya dolzhna byt' skorost' obolochki, pri kotoroi udarnaya volna obrazuetsya, naprimer, cherez 10⁴ let posle vspyshki sverhnovoi? Delo zdes' v tom, chto, kak pokazyvayut nablyudeniya, obolochka sverhnovoi v Krabovidnoi tumannosti sovsem ne zatormozilas', hotya eta sverhnovaya vspyhnula uzhe 10³ let nazad. S drugoi storony, obolochka tumannosti Petli v Lebede zatormozilas' ochen' sil'no. Eta sverhnovaya vspyhnula, veroyatno, okolo 10⁵ let nazad. Polagaya v (6.20) v₀ ≈ 10⁴ let, nahodim t₀ 10³ km/sek.

Po-vidimomu, srazu posle vspyshki sverhnovoi obrazuetsya teplovaya volna v mezhzvezdnom gaze. Veroyatno, zdes' imeet mesto besstolknovitel'naya dissipaciya energii i obolochka tormozitsya ne gazodinamicheskim putem. Lish' posle togo kak skorost' obolochki umen'shitsya do v ∼ 10³ km/sek, nachnetsya tormozhenie putem obrazovaniya udarnoi volny i, nachinaya s etogo vremeni, mozhno primenyat' reshenie zadachi o sil'nom vzryve.

Neskol'ko luchshe obstoit delo v sluchae dvizheniya obolochek novyh zvezd v plotnoi mezhzvezdnoi srede. Zdes' vremya obrazovaniya udarnoi volny vsego neskol'ko desyatkov let.

Posle togo kak znachitel'naya dolya energii, kak obolochki, tak i nagretoi mezhzvezdnoi sredy, vysvetilas' iz-za izlucheniya v ul'trafioletovoi i rentgenovskoi oblasti spektra, rasshirenie ne ostanavlivaetsya.

Bolee togo, poslednie dannye o rentgenovskih istochnikah pokazyvayut, chto vokrug vidimyh v optike nekotoryh tumannostei, ostatkov sverhnovyh, nablyudayutsya bol'shie po razmeru oblasti dovol'no intensivnogo rentgenovskogo izlucheniya. Napomnim, chto grafiki ris. 22 postroeny po dannym opticheskih nablyudenii i, sledovatel'no, oni opredelyayut skorost' razleta bolee plotnyh, no nizkotemperaturnyh oblastei. Menee plotnye, no bolee nagretye oblasti szhatogo mezhzvezdnogo gaza rasshiritsya s bol'shei skorost'yu, nesmotrya na zametnuyu poteryu energii na izluchenie.

Pri intensivnom izluchenii rasshirenie obolochki i szhatoi oblasti mezhzvezdnogo gaza opredelyaetsya uzhe ne polnoi energiei vzryva, a kolichestvom dvizheniya obolochki. Iz uravnenii sfericheski-simmetrichnogo dvizheniya gaza mozhno poluchit' sleduyushii strogii zakon izmeneniya kolichestva dvizheniya:

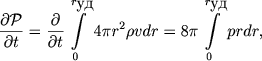
$\frac{\partial \mathcal{P}}{\partial t} = \frac{\partial}{\partial t}\int\limits_0^{r_{\mbox{ud}}}4\pi r^2\rho v dr = 8\pi \int\limits_0^{r_{\mbox{ud}}} prdr,$ (6.21)

gde $\mathcal{P}$ polnoe kolichestvo dvizheniya obolochki i mezhzvezdnogo gaza*). Esli iz-za vysvechivaniya davlenie gaza vnutri oblasti, ohvachennoi dvizheniem, ochen' bystro umen'shaetsya i padaet do nulya, to mozhno schitat' kolichestvo dvizheniya obolochki $\mathcal{P}$ sohranyayusheisya velichinoi i prinyat' $\mathcal{P}$ v kachestve opredelyayushego parametra vmesto energii vspyshki.

Togda zakon rasprostraneniya perednego fronta rasshiryayusheisya oblasti mezhzvezdnogo gaza imel by takoi vid:

$r_{\mbox{ud}} \approx \left(\frac{\mathcal{P}}{\rho}\right)^{1/4}t^{1/4}.$ (6.22)

Kak legko pokazat', esli povtorit' vse privedennye vyshe rassuzhdeniya i uchest', chto teper' v opredelyayushem parametre $B = \frac{\mathcal{P}}{\rho}$ , my imeem k₃ = 4, k₄ = -1.

Skorost' perednego fronta etoi oblasti

$v_{\mbox{ud}} = \frac{1}{4}\left(\frac{\mathcal{P}}{\rho}\right)^{1/4}t^{-3/4} \approx \frac{1}{4}\frac{\mathcal{P}}{\rho r_{\mbox{ud}}^3}.$

Kak i sledovalo ozhidat', zdes' tormozhenie bolee bystroe. Vprochem, veroyatno, eto reshenie imeet ochen' ogranichennuyu oblast' primeneniya, poskol'ku ono trebuet, kak uzhe otmechalos', obrasheniya v nul' pravoi chasti (6.21). Maloveroyatno, chtoby v real'nyh astrofizicheskih usloviyah vysvechivanie gaza bylo by nastol'ko sil'nym, chto davlenie mezhzvezdnoi sredy v oblasti vspyshki bylo by ochen' malym. Napomnim, chto, kak pokazyvayut nablyudeniya, pri vspyshkah sverhnovyh obrazuetsya bol'shoe kolichestvo relyativistskih elektronov, davlenie kotoryh otnyud' ne malo.

K avtomodel'nym dvizheniyam otnositsya sluchai razleta gaza v pustotu, kotoryi takzhe mozhet naiti primenenie v astrofizike. Predpolozhim, chto u ogranichennogo ob'ema gaza s ravnomernoi plotnost'yu i temperaturoi vnezapno udalili stenku. Togda po gazu vnutr' pobezhit volna razrezheniya, a s otkrytoi storony nachnetsya istechenie. Esli net protivodavleniya izvne, to opredelyayushimi parametrami budut plotnost' gaza ρ i skorost' zvuka $v_s = \sqrt{\gamma\frac{\Re T_0}{\mu}}$ gde T₀ - temperatura gaza do udaleniya stenki. Zdes' parametr V mozhno priravnyat' v i, sledovatel'no, dvizhenie opisyvaetsya sootnosheniem

$r = \lambda v_s t.$ (6.23)

Dlya perednego fronta razletayushegosya gaza v ploskom sluchae (odnomernom dvizhenii vdol' odnoi koordinaty) imeem λ = 2(γ - 1)^-1. Dlya cilindricheski- i sfericheski-simmetrichnyh dvizhenii prostyh analiticheskih formul poluchit' ne udavalos', no bylo pokazano, chto po krainei mere pri γ = 3 takzhe λ = 1 [8], tak chto mozhno schitat' uslovie dlya skorosti perednego fronta razletayushegosya gaza

$v \approx \frac{2v_s}{\gamma - 1} \approx 3v_s.$ (6.24)

dostatochno obshim. Predpolozhenie o tom, chto gaz razletaetsya v pustotu so skorost'yu v tri raza bol'shei skorosti zvuka v pokoyasheisya srede, chasto ispol'zuetsya v astrofizike.

Avtomodel'nyi metod byl primenen G. S. Bisnovatym-Koganom, Ya. B. Zel'dovichem i D. K. Nadezhinym [14] i dlya analiza obratnoi zadachi - akkrecii gaza na zvezdu. Esli schitat', chto massa akkreciruyushego gaza mnogo men'she massy samoi zvezdy, to ostayutsya dva opredelyayushih parametra - uskorenie sily tyazhesti g i nachal'naya plotnost' akkreciruyushego gaza. Pri nabeganii gaza na zvezdu na nekotorom rasstoyanii ot nee obrazuetsya udarnaya volna, uhodyashaya ot ee poverhnosti. Osnovnoi zadachei yavlyaetsya opredelenie skorosti dvizheniya etoi udarnoi volny. Zdes' bezrazmernyi argument

$\lambda = \frac{4r}{gt^2}.$ (6.25)

Na fronte udarnoi volny dolzhno byt' λ = λ_ud = const. Poetomu udarnaya volna uskoryaetsya po mere udaleniya ot poverhnosti zvezdy, na kotoruyu vypadaet akkreciruyushii gaz:

$v_{\mbox{ud}} = \frac{1}{2}\lambda_{\mbox{ud}}gt.$ (6.26)

Razumeetsya, eto formula spravedliva, poka g schitaetsya postoyannoi, t. e. poka udarnaya volna ne otoidet ot zvezdy na rasstoyanie, sravnimoe s ee radiusom. Velichinu λ_ud mozhno opredelit' tol'ko putem chislennogo resheniya avtomodel'nyh uravnenii dvizheniya. V rabote [14] byli polucheny znacheniya: λ_ud = 0,3154 pri γ = 5/3 i λ_ud = 0,1521 pri γ = 4/3. Massa gaza, zaklyuchennaya mezhdu poverhnost'yu zvezdy i udarnoi volnoi, uvelichivaetsya so vremenem kak ¼ξρgt, gde chislennoe znachenie mnozhitelya ξ = 2,256 pri γ = 5/3 i ξ = 2,075 pri γ = 4/3.

Avtory raboty [14] otmechayut, chto esli dopustit', chto akkreciruyushii gaz besprepyatstvenno provalivaetsya pod poverhnost' zvezdy ("chernaya dyra"), to ξ = 2.

*) Formula (6.21) poluchena V. S. Imshennikom.

<< § 5.4 Cirkulyaciya v atmosferah planet | Oglavlenie | § 6.2 Ionizacionnye fronty i udarnye volny vysvechivaniya v mezhzvezdnom prostranstve >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

$\frac{\partial v}{\partial t} + v\frac{\partial v}{\partial r} + \frac{1}{\rho}\frac{\partial p}{\partial r} = 0,$	(6.4)
$\frac{\partial \rho}{\partial t} + \frac{\partial}{\partial r}(\rho v) + (\nu - 1)\frac{\rho v}{r} = 0,$	(6.5)
$\frac{\partial}{\partial t}\left(\frac{p}{\rho^\gamma}\right) + v \frac{\partial}{\partial r}\left(\frac{p}{\rho^\gamma}\right) = 0.$	(6.6)