Astronet > Razmernosti i podobie astrofizicheskih velichin

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 6.1 Uravneniya avtomodel'nogo dvizheniya kosmicheskogo gaza | Oglavlenie | § 6.3 Avtomodel'nye dvizheniya v zvezdah i protozvezdah >>

§ 6.2 Ionizacionnye fronty i udarnye volny vysvechivaniya v mezhzvezdnom prostranstve

Ionizacionnye fronty predstavlyayut soboi specificheskoe yavlenie mezhzvezdnoi gazodinamiki, ne imeyushee analoga v zemnyh usloviyah. Napomnim fizicheskuyu kartinu etogo yavleniya. Pust' goryachaya zvezda s intensivnym potokom ul'trafioletovogo izlucheniya, sposobnogo ionizovat' vodorod, nahoditsya v oblasti, zapolnennoi mezhzvezdnym gazom. V okruzhayushei zvezdu oblasti vodorod ionizovan pochti polnost'yu - eto tak nazyvaemaya zona Stremgrena N II, rassmatrivaemaya eshe v gl. 1. Vdali ot goryachei zvezdy mezhzvezdnyi vodorod ostalsya neionizovannym - eto oblast' N I. Mozhno pokazat', chto granica mezhdu zonami N II i N I sravnitel'no uzkaya, ee tolshina sostavlyaet ne bolee neskol'kih procentov ot radiusa zony Stremgrena (sm., naprimer. [15]). Poetomu granicu mezhdu zonami N I i N II mozhno rassmatrivat' kak nekotoryi front, na kotorom temperatura i stepen' ionizacii menyayutsya skachkom. V zonah N I vodorod polnost'yu neitralen i, veroyatnee vsego, nahoditsya v molekulyarnom sostoyanii. Zdes' temperatura gaza poryadka ili men'she 100 œK v bolee plotnyh oblastyah i mozhet byt' neskol'ko vyshe, do 10³ œK, v razrezhennyh oblastyah. V zonah N II vodorod pochti polnost'yu ionizovan i temperatura gaza zdes' 8000 - 10 000œ.

Takim obrazom, po obe storony ionizacionnogo fronta davlenie gaza neodinakovo, chto dolzhno privodit' k dvizheniyu ionizacionnogo fronta v storonu zony N I. Krome togo, so storony goryachei zvezdy na ionizacionnyi front vse vremya padaet potok ionizuyushih kvantov. Eto oznachaet, chto cherez ionizacionnyi front vse vremya peretekaet gaz iz oblasti N I v oblast' N II. Issledovanie dinamiki etogo peretekaniya (ili, chto odno i to zhe, dvizheniya ionizacionnogo razryva v storonu N I) i sostavlyaet odin iz vazhnyh razdelov mezhzvezdnoi gazodinamiki. V chastnosti, zdes' nashli primenenie i metody teorii avtomodel'nogo dvizheniya. My ne budem rassmatrivat' vse voprosy teorii ionizacionnyh frontov (sm. [5, 15, 16]), a ogranichimsya lish' obsuzhdeniem primeneniya metodov teorii avtomodel'nogo dvizheniya. Odnako prezhde nam ponadobyatsya nekotorye sootnosheniya kak obshei teorii udarnyh voln s vysvechivaniem, tak i teorii ionizacionnyh frontov.

Nachnem s teorii udarnyh voln s vysvechivaniem (sm. [5]). Rassmotrim takuyu kartinu dvizheniya. Pust' v oblasti nepodvizhnogo holodnogo gaza s temperaturoi T₁ dvizhetsya sil'naya udarnaya volna, szhimayushaya gaz i nagrevayushaya ego do nekotoroi vysokoi temperatury T₂^*. Esli T₂^* poryadka (ili ne namnogo vyshe) temperatury 10³ gradusov, to v szhatoi i nagretoi oblasti udarnoi volny voznikaet sil'noe izluchenie, bystro ohlazhdayushee gaz. Iz-za etogo gaz v udarnoi volne prodolzhaet szhimat'sya, chto eshe bol'she ego ohlazhdaet. Nakonec, pri nekotoroi temperature T₂ intensivnoe izluchenie mozhet zametno umen'shit'sya i gaz opyat' pridet v nekotoroe, voobshe govorya, novoe sostoyanie teplovogo ravnovesiya. Temperatura T₂ mozhet byt' i ravna T₁, esli fizicheskoe sostoyanie gaza ne ochen' izmenilos' (naprimer, esli v udarnoi volne ne menyaetsya sostoyanie ionizacii i dissociacii molekul). Odnako obychno v udarnoi volne proishodyat neobratimye izmeneniya i poetomu novaya ravnovesnaya temperatury T₂ veroyatno, zametno bol'she T₁.

Predpolozhim, chto vsya kartina rassmotrennogo dvizheniya stacionarna. Togda iz usloviya sohraneniya massy i potoka impul'sa gaza pri protekanii ego cherez oblast' szhatiya i vysvechivaniya mozhno poluchit' dva sootnosheniya, svyazyvayushie izmenenie plotnosti gaza i ego skorosti po obe storony etoi oblasti. Napomnim, chto v silu vysvechivaniya potok energii ne sohranyaetsya.

Usloviya sohraneniya potoka massy i impul'sa imeyut vid

$\rho_1 v_1 = \rho_2 v_2,$ (6.27)

$\rho_1\left(v_1^2 + \frac{\Re T_1}{\mu_1}\right) = \rho_2\left(v_2^2 + \frac{\Re T_2}{\mu_2}\right),$ (6.28)

gde ρ₁ i ρ₂ - plotnost' gaza do i posle fronta volny, v₁ - skorost' vtekaniya gaza v oblast' szhatiya i vysvechivaniya, v₂ - skorost' ego vytekaniya iz etoi oblasti. Poskol'ku sostoyanie gaza menyaetsya, to molekulyarnye vesa μ₁ i μ₂ mogut byt' razlichnymi. Sleduet podcherknut', chto v etom paragrafe pod v vsegda ponimaetsya skorost' gaza po otnosheniyu k frontu razryva.

Esli schitat', chto udarnaya volna szhatiya i vysvechivaniya dvizhetsya v nepodvizhnom gaze i chto skorost' udarnoi volny zadana, to v (6.27) - (6.28) sleduet schitat' ρ₁, v₁, T₁/μ₁ i T₂/μ₂ zadannymi i togda eta sistema opredelyaet ρ₂ i v₂. Reshenie sistemy (6.27) - (6.28) ochevidno:

$\begin{array}{ll} \frac{\rho_1}{\rho_2} = \frac{v_2}{v_1} = &\frac{1}{2} \left[1 + \frac{\Re T_1}{\mu_1 v_1^2} \pm \sqrt{\left(1 + \frac{\Re T_1}{\mu_1 v_1^2}\right)^2 - \frac{4\Re T_2}{\mu_2 v_1^2}}\right] \approx \\ & \approx \frac{1}{2} \left(1 \pm \sqrt{1 - \frac{4\Re T_2}{\mu_2 v_1^2}} \right). \end{array}$ (6.29)

V poslednem ravenstve uchteno, chto v sil'nyh udarnyh volnah s vysvechivaniem skorost' udarnoi volny v₁ mnogo bol'she skorosti zvuka v pokoyashemsya gaze v_1s = (γT₁/μ₁)^½. Mozhno takzhe ubedit'sya, chto i chlen $\frac{4\Re T_2}{\mu_2 v_1^2}$ mal po sravneniyu s edinicei. V samom dele, maksimal'naya temperatura v oblasti szhatiya T₂^* poryadka kineticheskoi energii volny, otnesennoi k odnoi chastice, t. e. $T_2* \sim \frac{m_H}{\Re}v_1^2$ . Esli vysvechivanie zametno, to T₂ ≪ T₂^* i poetomu vmesto (6.29) mozhno napisat' dva resheniya v vide

$\frac{\rho_2}{\rho_1} = \frac{v_1}{v_2} \approx \frac{\mu_2 v_1^2}{\Re T_2},$ (6.30)

$\frac{\rho_2}{\rho_1} = \frac{v_1}{v_2} = 1 + \frac{\Re T_2}{\mu_2 v_1^2}.$ (6.31)

Vtoroe reshenie sootvetstvuet slaboi volne szhatiya s vysvechivaniem maloi amplitudy i v dal'neishem rassmatrivat'sya ne budet.

Reshenie (6.30) opisyvaet sil'nuyu volnu uplotneniya (ρ₂ ≫ ρ₁) s vysvechivaniem gaza. My ne budem rassmatrivat' strukturu udarnoi volny s vysvechivaniem (sm., naprimer, [5, 12, 13]), otmetim lish', chto podavlyayushaya chast' potoka kineticheskoi energii v sil'noi udarnoi volne

$F = \frac{1}{2}\rho_1 v_1^3$ (6.32)

prevrashaetsya v izluchenie i uhodit iz oblasti szhatiya. Po formule (6.32) mozhno srazu opredelit' potok polnogo (prointegrirovannogo po vsemu spektru) izlucheniya fronta udarnoi volny s vysvechivaniem.

Teper' pereidem k ionizacionnym frontam. Zdes' est' mnogo obshego s udarnymi volnami s vysvechivaniem, hotya struktury takoi udarnoi volny i ionizacionnogo fronta sushestvenno razlichayutsya. My obsudim eto razlichie podrobnee nizhe, a seichas ogranichimsya nekotorymi obshimi zamechaniyami. Neionizovannyi gaz, vtekaya v oblast' ionizacionnogo fronta, pogloshaet ionizuyushie kvanty, pri etom ionizuetsya i nagrevaetsya. Zatem nachinaetsya vysvechivanie teplovoi energii i temperatura opyat' padaet uzhe v oblasti pochti polnoi ionizacii. Okonchatel'naya temperatura za frontom ionizacionnogo fronta, dlya kotoroi my sohranim oboznachenie T₂, takzhe opredelena usloviem ravnovesiya s izlucheniem.

Eto oznachaet, chto sistema (6.27) i (6.28) spravedliva i dlya ionizacionnyh frontov s tem sushestvennym dopolneniem, chto potok massy cherez ionizacionnyi front teper' opredelen potokom ionizuyushih kvantov. V samom dele, chislo atomov vodoroda, peresekayushih ionizacionnyi front, dolzhno ravnyat'sya chislu ionizuyushih kvantov, popadayushih na etot front iz oblasti N II. Poetomu vmesto (6.27) teper' zapishem

$\rho_1 v_1 = \rho_2 v_2 = \mu_1 m_H J,$ (6.33)

gde m_H - massa atoma vodoroda, a J - potok ionizuyushih kvantov na edinicu poverhnosti ionizacionnogo fronta. Sistema uravnenii (6.28) i (6.33) opredelyaet svoistva ionizacionnyh frontov. Otlichie ot udarnoi volny s vysvechivaniem zaklyuchaetsya v tom, chto teper' skorost' v₁ dvizheniya ionizacionnogo fronta po neionizovannomu gazu opredelyaetsya potokom ionizuyushih kvantov:

$v_1 = \frac{\mu_1 m_H J}{\rho_1} = \frac{J}{n_H},$ (6.34)

gde n_H - koncentraciya atomov vodoroda v zone N I. Reshenie (6.29) ostaetsya spravedlivym i zdes', tol'ko teper' nel'zya schitat' velichiny $kT_1/\mu_1m_H v_1^2$ ili $kT_2/\mu_1 m_H v_2^2$ , malymi pri lyubyh usloviyah.

Iz trebovaniya veshestvennosti (6.29) sleduet ogranichenie

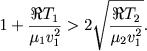
$1 + \frac{\Re T_1}{\mu_1 v_1^2} > 2\sqrt{\frac{\Re T_2}{\mu_2 v_1^2}}.$ (6.35)

Otsyuda sleduyut usloviya, nalagaemye na skorost' ionizacionnogo fronta otnositel'no gaza v N I. Iz (6.35) nahodim, chto neravenstvo vypolnyaetsya, esli

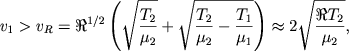
$v_1 > v_R = \Re^{1/2}\left(\sqrt{\frac{T_2}{\mu_2}} + \sqrt{\frac{T_2}{\mu_2} - \frac{T_1}{\mu_1}}\right) \approx 2\sqrt{\frac{\Re T_2}{\mu_2}},$ (6.36)

libo esli

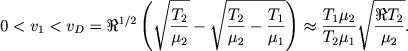
$0 < v_1 < v_D = \Re^{1/2}\left(\sqrt{\frac{T_2}{\mu_2}} - \sqrt{\frac{T_2}{\mu_2} - \frac{T_1}{\mu_1}}\right) \approx \frac{T_1\mu_2}{T_2\mu_1}\sqrt{\frac{\Re T_2}{\mu_2}}.$ (6.37)

Zdes' v_R i v_D - znacheniya skorostei ionizacionnyh frontov, ogranichivayushie raznye rezhimy techeniya gaza.

Kombiniruya neravenstva (6.36) i (6.37) s sootnosheniem (6.34), nahodim usloviya obrazovaniya ionizacionnyh frontov pri zadannom potoke ionizuyushih kvantov J i plotnosti gaza v zone N I. Eti usloviya otrazheny v klassifikacii ionizacionnyh frontov po Kanu [17].

1. Ionizacionnyi front R-tipa, rasprostranyayushiisya v razrezhennoi oblasti N I. Uslovie na plotnost' gaza imeet vid

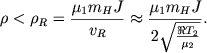
$\rho < \rho_R = \frac{\mu_1 m_H J}{v_R} \approx \frac{\mu_1 m_H J}{2\sqrt{\frac{\Re T_2}{\mu_2}}}.$ (6.38)

Pri etom iz (6.29) sleduet, chto vozmozhny dva tipa R-fronta. V odnom iz nih gaz v N I ottekaet ot fronta so sverhzvukovoi skorost'yu, t. e. $v_2 > \sqrt{\frac{\Re T_2}{\mu_2}}$ , a v drugom tipe R-fronta $v_2 < \sqrt{\frac{\Re T_2}{\mu_2}}$ . Prinyato nazyvat' pervyi sluchai sil'nym R-frontom, a vtoroi sluchai - slabym R-frontom. I v tom i v drugom sluchae plotnost' gaza pri prohozhdenii ionizacionnogo fronta uvelichivaetsya.

2. Kriticheskii ionizacionnyi front R-fronta, pri kotorom v₂ = v_R i neravenstvo (6.38) zamenyaetsya na ravenstvo. Za ionizacionnym frontom $v_2 = \sqrt{\frac{\Re T_2}{\mu_2}}$ - eto izvestnoe v gazodinamike uslovie tochki Zhuge. V kriticheskom ionizacionnom fronte R-tipa takzhe imeet mesto uplotnenie gaza. Zdes' vazhno to, chto ottok gaza v N II ot fronta proishodit s mestnoi izotermicheskoi skorost'yu zvuka, no zato etot front pri zadannom J mozhet rasprostranyat'sya tol'ko v srede s fiksirovannoi plotnost'yu ρ_R.

3. Ionizacionnyi front D-tipa, rasprostranyayushiisya v bolee plotnoi oblasti neionizovannogo gaza. Uslovie na plotnost' gaza v N I imeet vid

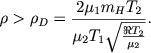
$\rho > \rho_D = \frac{2\mu_1 m_H T_2}{\mu_2 T_1\sqrt{\frac{\Re T_2}{\mu_2}}}.$ (6.39)

Zdes' takzhe imeyut mesto dva tipa D-frontov: sil'nyi front, v kotorom $v_2 > \sqrt{\frac{\Re T_2}{\mu_2}}$ i slabyi front s $v_2 < \sqrt{\frac{\Re T_2}{\mu_2}}$ . V oboih sluchayah na ionizacionnyh frontah D-tipa proishodit razrezhenie plotnogo gaza pri popadanii ego v oblast' N II.

4. Kriticheskii front D-tipa, pri kotorom v₂ = v_D i neravenstvo (6.39) prevrashaetsya v ravenstvo. Zdes' takzhe vypolneno uslovie tochki Zhuge: i $v_2 = \sqrt{\frac{\Re T_2}{\mu_2}}$ , i kriticheskie fronty D-tipa pri zadannom znachenii potoka ionizuyushih kvantov mogut rasprostranyat'sya lish' v oblasti N II s fiksirovannoi plotnost'yu ρ_D.

5. Ionizacionnye fronty M-tipa, kotorye rasprostranyayutsya v zone N I s plotnost'yu sredy

$\rho_R < \rho < \rho_D.$

Iz izlozhennogo vyshe yasno, chto ionizacionnye fronty M-tipa v chistom vide sushestvovat' ne mogut. Pered ionizacionnym frontom takogo tipa dvizhetsya libo volna uplotneniya, uvelichivayushaya plotnost' gaza v N I do ρ > ρ_D, libo volna razrezheniya, ponizhayushaya plotnost' gaza v N I do ρ < ρ_R.

Nado otmetit', chto po mere peremesheniya v odnorodnoi oblasti N I tip ionizacionnogo fronta mozhet izmenyat'sya, poskol'ku pri etom menyaetsya i velichina potoka ionizuyushih kvantov. Pri udalenii ot zvezdy potok umen'shaetsya kak J ∼ r², no velichina J mozhet menyat'sya i za schet evolyucii zvezdy - s techeniem vremeni menyayutsya svetimost' i poverhnostnaya temperatura. Krome togo, s udaleniem fronta rastet i pogloshenie etih kvantov. Po-vidimomu, pri vozgoranii goryachei zvezdy v oblasti neionizovannogo vodoroda snachala pri bol'shom J obrazuetsya blizkii k zvezde ionizacionnyi front sil'nogo R-tipa. Zatem on perehodit v kriticheskii front R-tipa. Zdes' zakanchivaetsya formirovanie obychnoi zony N II. Ee granica prodolzhaet rasshiryat'sya v oblasti N I, sozdavaya vperedi udarnuyu volnu, a zatem, po mere padeniya J, ionizacionnyi front priobretaet harakteristiki D-tipa [15].

Detal'naya struktura ionizacionnyh frontov rassmatrivalas' vo mnogih rabotah (obzor sm. v [16]). V chastnosti, v rabote [18] bylo polucheno uravnenie, opredelyayushee temperaturu T₂ po zadannoi temperature ionizuyushei zvezdy T_∗, esli schitat', chto spektral'noe raspredelenie potoka ionizuyushih kvantov J opisyvaetsya formuloi Planka s T = T_∗. Dlya T₂ v gradusah Kel'vina imeem uravnenie:

$\frac{3}{2} T_2 + \frac{T_2^{3/4}}{1600^{7/4}}(T_2 - 4000)^2 = T_*.$ (6.40)

Pri izmenenii T_∗ ot 20 do 80 tysyach gradusov velichina T₂ menyaetsya ot 6500 do 9400 œK.

Osnovnoi problemoi teorii ionizacionnyh frontov yavlyaetsya raschet ih dvizheniya v mezhzvezdnoi srede. V naibolee prostoi postanovke zadacha zaklyuchaetsya v sleduyushem. Pust' v odnorodnoi zone N I vspyhnula goryachaya zvezda. Snachala volna ionizacii rasprostranyaetsya bystro i net zametnyh gazodinamicheskih effektov. Cherez kakoe-to vremya na nekotorom rasstoyanii ot zvezdy obrazuetsya kvazistacionarnyi ionizacionnyi front, kotoryi zatem otnositel'no medlenno prodvigaetsya vnutr' oblasti N I. Eto dvizhenie my i budem rassmatrivat', ispol'zovav metody teorii avtomodel'nogo dvizheniya. Razumeetsya, eti metody dayut tol'ko ogranichennye rezul'taty, no, kak okazalos', oni kachestvenno soglasuyutsya i s rezul'tatami, poluchennymi pri bolee tochnyh chislennyh raschetah. Obzor razlichnyh metodov rascheta dvizheniya ionizacionnyh frontov dan v rabote [19].

Primenenie metoda avtomodel'nyh dvizhenii k ionizacionnym frontam bylo dano S. A. Kaplanom [5]. Eta zadacha takzhe rassmatrivalas' v rabotah [20-23]. Naibolee polnye chislennye resheniya dany v rabotah [23, 24].

Dlya avtomodel'nosti dvizheniya neobhodimo imet' tol'ko dva osnovnyh opredelyayushih parametra. Odin iz nih ocheviden - eto plotnost' gaza v oblasti N I, oboznachaemaya v dal'neishem kak ρ₁ Vtorym parametrom, voobshe govorya, mozhno vybrat' svetimost' zvezdy v diapazone chastot ionizuyushih kvantov. Tak i sdelano v rabotah [20, 21]. Odnako, poskol'ku pri etom potok pryamyh (t. e. idushih ot zvezdy) ionizuyushih kvantov padaet kak r^-2 po mere rasprostraneniya ionizovannogo fronta, to dlya sohraneniya avtomodel'nosti prihoditsya dopuskat' opredelennuyu zavisimost' plotnosti v N I ot rasstoyaniya do zvezdy i rassmatrivat' cilindricheski-simmetrichnuyu zadachu.

V rabote [22] sohranena sfericheskaya simmetriya i postoyannaya nachal'naya plotnost', no predpolozheno, chto ionizuyushaya svetimost' zvezdy rastet so vremenem kak t³.

Strogo govorya, u nas net osnovanii schitat' polnuyu moshnost' ionizuyushih kvantov, padayushih iznutri na ves' ionizacionnyi front, nekotoroi fiksirovannoi velichinoi - postoyannoi ili menyayusheisya so vremenem opredelennym obrazom. Krome pryamyh ionizuyushih kvantov ot zvezdy est' eshe i diffuznye ionizuyushie kvanty, kolichestvo kotoryh takzhe mozhet menyat'sya s izmeneniem geometrii zony NI ili so vremenem. Po nashemu mneniyu, bolee harakternym opredelyayushim parametrom yavlyaetsya temperatura T₂ na vnutrennei granice ionizacionnogo fronta, bolee ili menee odnoznachno, kak sleduet iz (6.40), opredelennaya poverhnostnoi temperaturoi ionizuyushei zvezdy T_∗.

S drugoi storony, potok ionizuyushih kvantov, po sushestvu, opredelyaet sam harakter ionizacionnogo fronta i ne uchityvat' etu velichinu pri analize dvizheniya ionizacionnogo fronta nel'zya. Eto oznachaet, chto v deistvitel'nosti issledovanie dvizheniya ionizacionnogo fronta ne svoditsya strogo k avtomodel'noi zadache. Tem ne menee my rassmotrim dvizhenie ionizacionnogo fronta kak avtomodel'nuyu zadachu, poskol'ku v etom sluchae mozhno poluchit' hotya i ne tochnye, no zato fizicheski naglyadnye resheniya.

V sootvetstvii s predpolozheniem ob avtomodel'nosti budem schitat' opredelyayushimi parametrami dve velichiny, postoyanstvo kotoryh vo vremeni naibolee chetko vyrazheno. Eto plotnost' gaza ρ i temperatura T_∗. Ochevidno, chto zadannymi mozhno schitat' plotnost' i temperaturu v nevozmushennoi zone N I, t. e. velichiny ρ₁ i T₁. Po usloviyu, mozhno schitat' zadannoi i temperaturu v zone N II, t. e. velichinu T₂ (opredelennuyu, naprimer, uravneniem (6.40)). No, krome togo, mozhno zadat' eshe nekotorye znacheniya parametrov v zone N II.

Ne ochen' yasno, naskol'ko mozhno trebovat' vypolneniya usloviya tochki Zhuge za ionizacionnym frontom (sm. [5]). Eto uslovie svoditsya k predpolozheniyu, chto ionizovannyi gaz ottekaet svobodno ot ionizacionnogo fronta, - t. e. ego dvizheniyu ne meshaet sama zona N II. Togda skorost' gaza po otnosheniyu k ionizacionnomu frontu ravna mestnoi skorosti zvuka, t. e. $v_2 = \sqrt{\frac{\Re T_2}{\mu_2}}$ , i ionizacionnaya volna okazyvaetsya kriticheskim frontom R- ili D-tipa. Pri etom odnoznachno opredeleny skorosti ionizacionnogo fronta otnositel'no gaza pered frontom, soglasno formulam (6.36) ili (6.37), a takzhe vse drugie parametry ionizacionnoi volny, kak, naprimer, skachok plotnosti.

No uslovie tochki Zhuge yavlyaetsya obyazatel'nym, esli ionizovannyi gaz ottekaet ot ionizacionnogo fronta v pustotu. Esli zhe vnutri zony N II uzhe imeetsya dostatochno ionizovannogo gaza, v kotorom skorost' zvuka ne mala (∼ 10 km/sek), to plotnost' gaza, a sledovatel'no, i davlenie vnutri zony N II uspevaet vyrovnyat'sya tak, chto gaz ottekaet ot ionizacionnogo fronta s nekotoroi men'shei skorost'yu, t. e. ionizacionnyi razryv mozhet byt' i sil'nogo i slabogo R- ili D-tipov. Uslozhnyaet zadachu i to, chto velichina J opredelyaetsya polnym potokom ionizuyushih kvantov, kak pryamyh idushih ot zvezdy, tak i diffuznyh, rasseyannyh v samoi zone II II i dostigayushih granicy etoi zony.

Razumnee vsego schitat', chto na vnutrennei storone ionizacionnogo fronta zadany plotnost' gaza ρ₂, temperatura T₂ i chto nam izvestna skorost' ottoka gaza v₂, opredelennaya po sootnosheniyu tipa (6.34):

$v_2 = \frac{\mu_1 m_H J}{\rho_2} = \frac{\mu_1 J}{\mu_2 n_p},$ (6.41)

gde J - potok ionizuyushih kvantov pa vnutrennei storone ionizacionnogo fronta i n_p - koncentraciya protonov (ili elektronov) v etoi oblasti. Esli vt est' skorost' ionizacionnogo fronta v prostranstve, to skorost' gaza za frontom etoi volny v nepodvizhnoi sisteme koordinat est' v₂ - v_i. Zametim, chto velichiny ρ₂, T₂ i v₂ - v_i mogut byt' v principe opredeleny nezavisimo drug ot druga po dannym nablyudenii.

Uravnenie dlya opredeleniya skachkov parametrov na fronte ionizacionnogo razryva tozhdestvenno s uravneniem (6.29), poskol'ku i zdes' ishodnaya sistema sovpadaet s (6.27) - (6.28). Napomnim, chto gee razlichie svoditsya k zadaniyu velichiny potoka ionizuyushih kvantov cherez etot front. Napomnim takzhe, chto skorosti v₁ i v₂est' skorosti gaza po otnosheniyu k frontu ionizacionnogo razryva (v₁ - v N I i v₂ v N II).

Teper' pereidem k formulirovke samoi avtomodel'noi zadachi dlya analiza dvizheniya ionizacionnogo fronta. Soglasno skazannomu vyshe opredelyayushimi parametrami budut:

$[A] = [\rho_2] = \mbox{g} \cdot \mbox{sm}^{-3}; \quad [B] = \left[\sqrt{\frac{\Re T_2}{\mu_2}}\right] = \mbox{sm} \cdot \mbox{sek}^{-1}.$ (6.42)

Sopostavlyaya (6.1) i (6.2), poluchaem znacheniya pokazatelei k₁ = -3, k₂ = 0, k₃ = 1, k₁ = -1, δ = 1. Parametr ϰ soglasno (6.11) raven nulyu. Poskol'ku temperatura schitaetsya opredelyayushim parametrom, to dvizhenie mozhno schitat' izotermicheskim, sledovatel'no, primem γ = 1. I deistvitel'no, kak v zonah N I, tak i v zonah N II sushestvennuyu rol' igraet vzaimodeistvie s izlucheniem i poetomu temperatura deistvitel'no opredelyaetsya v pervuyu ochered' balansov poglosheniya i izlucheniya luchistoi energii.

Pri etih usloviyah avtomodel'nye uravneniya dvizheniya (6.8) - (6.10) okazyvayutsya elementarno prostymi:

$\frac{d\ln Z}{d \ln\lambda} = 2, \quad \frac{d\ln V}{d \ln\lambda} = \frac{\nu Z - (V-1)^2}{Z - (V-1)^2}, \quad \frac{d\ln R}{d \ln\lambda} = \frac{(\nu - 1)V(V-1)}{Z - (V-1)^2},$ (6.43)

gde

$\frac{d\ln Z}{d \ln\lambda} = 2, \quad \frac{d\ln V}{d \ln\lambda} = \frac{\nu Z - (V-1)^2}{Z - (V-1)^2}, \quad \frac{d\ln R}{d \ln\lambda} = \frac{(\nu - 1)V(V-1)}{Z - (V-1)^2},$ (6.44)

Prezhde chem idti dal'she, sdelaem odno zamechanie. V obshih uravneniyah avtomodel'nyh dvizhenii (6.8) - (6.10) est' osobaya tochka, v kotoroi vypolnyaetsya uslovie Z = (V - δ)². V sluchae (6.43) uslovie osoboi tochki: Z = (V - 1)². Dlya strogo ploskogo dvizheniya (t. e. pri ν = 1) eta osobaya tochka prevrashaetsya v osoboe reshenie, poskol'ku zdes' i chisliteli vtorogo i tret'ego uravnenii (6.43) obrashayutsya v nul'. Reshenie Z = (V - 1)² issledovano v [5]. Odnako dlya neploskih dvizhenii uslovie Z = (V - 1)² uzhe ne yavlyaetsya osobym resheniem, a lish' osoboi tochkoi. Poskol'ku real'naya struktura ionizacionnogo fronta ne. opisyvaetsya strogo odnomernym resheniem, to eto osoboe reshenie est' vyrozhdennyi sluchai i vryad li osushestvlyaetsya v deistvitel'nosti. Zdes' eto reshenie rassmatrivat'sya ne budet.

Iz (6.43) sleduet, chto dlya ploskogo odnomernogo dvizheniya (ν = 1) neosoboe reshenie nahoditsya srazu:

$Z = \frac{const}{\lambda^2}, \quad R = const, \quad V = \frac{const}{\lambda},$ (6.45)

gde konstanty opredelyayutsya granichnymi usloviyami. Pri etom nuzhno imet' v vidu, chto (6.45) spravedlivo tol'ko dlya oblasti nepreryvnogo techeniya i chto na ionizacionnom razryve i na fronte udarnoi volny znacheniya konstant v (6.45) takzhe menyayutsya skachkom.

Oboznachim cherez λ_i znachenie parametra λ na fronte ionizacionnogo razryva, t. e. budem schitat' skorost' ionizacionnogo fronta v prostranstve ravnoi

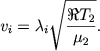
$v_i = \lambda_i\sqrt{\frac{\Re T_2}{\mu_2}}.$ (6.46)

Rassmotrim snachala prosteishuyu zadachu. Pust' po gazu v zone N I s plotnost'yu ρ₁ dvizhetsya odinochnyi ionizacionnyi razryv. Poskol'ku plotnost' v N II tozhe zadana, to izvesten skachok plotnosti

$\frac{\rho_1}{\rho_2} = R_1(\lambda_i).$ (6.47)

Soglasno usloviyu (6.41) my znaem i velichinu v₂, a sledovatel'no, i velichinu V₂(λ_i) dlya bezrazmernoi skorosti v nepodvizhnoi sisteme koordinat. Otsyuda imeem

$v_2 = v_i - \frac{r}{t}V_2(\lambda_i) = \sqrt{\frac{\Re T_2}{\mu_2}}\lambda_i [1-V_2(\lambda_i)],$ (6.48)

esli, konechno, opredelena velichina λ_i. Dlya ee nahozhdeniya vospol'zuemsya usloviem (6.29), kotoroe v bezrazmernyh peremennyh priobretaet vid

$R_1(\lambda_i) = 1 - V(\lambda_i) = \frac{1}{2}\left[1 + \frac{\mu_2 T_1}{\mu_1 T_2}\frac{1}{\lambda_i^2} \pm \sqrt{\left(1 + \frac{\mu_2 T_1}{\mu_1 T_2}\frac{1}{\lambda_i^2}\right)^2 - \frac{4}{\lambda_i^2}}\right].$ (6.49)

My imeem dva uravneniya, kazhdoe iz kotoryh nezavisimo opredelyaet V₂(λ_i) i λ_i. Yasno, chto poluchennye takim obrazom znacheniya velichin, kak pravilo, ne budut udovletvoryat' (6.48) dlya zadannogo znacheniya v₂. Zadacha okazalas' pereopredelennoi.

Vyhodov iz etogo zatrudneniya dva. Naprimer, mozhno bylo by schitat', chto parametry zony N II proizvol'ny, t. e. neizvestny po otdel'nosti ρ₂ i v₂ (no, po-prezhnemu, zadano ih proizvedenie (6.41)). Togda (6.49) sleduet rassmatrivat' kak dva uravneniya, opredelyayushie R₁(λ_i) i V₂(λ_i). Dlya nahozhdeniya λ_i zapishem (6.41) v bezrazmernom vide:

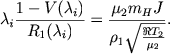
$\lambda_i\frac{1 - V(\lambda_i)}{R_1(\lambda_i)} = \frac{\mu_2 m_H J}{\rho_1 \sqrt{\frac{\Re T_2}{\mu_2}}} .$ (6.50)

Podstavlyaya syuda V(λ_i) i R₁(λ_i) iz (6.49), nahodim λ_i.

Odnako etot sluchai osushestvlyaetsya, veroyatno, redko. Bolee veroyaten vtoroi sluchai, kogda ionizacionnyi front sozdaet pered soboi udarnuyu volnu, szhimayushuyu gaz v zone N I tak, chtoby po nei uzhe mogla by rasprostranyat'sya ionizacionnaya volna s parametrami, opredelennymi ionizuyushei zvezdoi zadannogo tipa.

Zdes' mogut byt' razlichnye kombinacii dvizhenii, no my rassmotrim prostoi i ves'ma veroyatnyi sluchai, kogda ionizuyushaya zvezda sozdaet rasshiryayushuyusya obolochku v oblasti N I. Na perednem fronte etoi obolochki idet udarnaya volna, szhimayushaya gaz v N I, a ee zadnii front predstavlyaet soboi ionizacionnyi front D-tipa, na kotorom proishodit razrezhenie i ionizaciya gaza. Takie obolochki deistvitel'no chasto nablyudayutsya vokrug zon Stremgrena, sozdannyh ochen' goryachimi zvezdami. Struktura takih obolochek rassmatrivalas' v rabotah [5, 23, 24]. Dlya analiza etoi zadachi my i ispol'zuem opisannyi vyshe avtomodel'nyi metod.

Pust' polozheniyu udarnoi volny sootvetstvuet znachenie λ_s, t. e. ee skorost' dvizheniya po nepodvizhnomu gazu N I est'

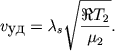
$v_{\mbox{ud}} = \lambda_s\sqrt{\frac{\Re T_2}{\mu_2}}.$ (6.51)

Ochevidno, chto λ_s > λ_i i oblast' λ_s - λ_i sootvetstvuet szhatoi dvizhusheisya obolochke gaza N I. Radi prostoty budem schitat', chto temperatura T'₁ v etoi obolochke ravna temperature T₁ v nevozmushennoi oblasti N I. Eto ogranichenie ne obyazatel'no i v knige [5] rassmotreno uslovie T'₁ > T₁. Shtrihovannymi velichinami budem oboznachat' znacheniya parametrov v dvizhusheisya obolochke N I. Esli λ_s = λ_i to tolshina obolochki ostaetsya neizmennoi, pri λ_s > λ_i obolochka rasshiryaetsya. Esli skorost' rasshireniya obolochki otnositel'no nevelika - uslovie, kotoroe chasto vstrechaetsya i kotoroe my budem schitat' vypolnennym, to

$\lambda_s - \lambda_i = \Delta\lambda \ll \lambda_i.$

Iz (6.29), schitaya, po-prezhnemu, zadannoi velichinu ρ₁/ρ₂ = R₁(λ_s) - otnoshenie zadannyh plotostei v zone N II i nevozmushennoi zone N I, nahodim uravneniya zavisimosti ot Xs dlya sleduyushih velichin: ρ'₂ = ρ₂R'₂(λ_s) - plotnosti gaza v obolochke srazu za frontom udarnoi volny i $V'_2(\lambda_s)\sqrt{\frac{\Re T_2}{\mu_2}}$ - skorosti dvizheniya gaza (v nepodvizhnoi sisteme koordinat) takzhe srazu za frontom udarnoi volny. Imeem

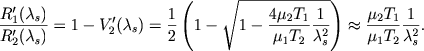
$\frac{R'_1(\lambda_s)}{R'_2(\lambda_s)} = 1 - V'_2(\lambda_s) = \frac{1}{2}\left(1 - \sqrt{1 - \frac{4\mu_2 T_1}{\mu_1 T_2}\frac{1}{\lambda_s^2}}\right) \approx \frac{\mu_2 T_1}{\mu_1 T_2}\frac{1}{\lambda_s^2}.$ (6.52)

Zdes' T₁ ≪ T₂ i λ_s ne maló po sravneniyu s edinicei, inymi slovami, skorost' obolochki bol'she skorosti zvuka v N I. Poslednee ravenstvo spravedlivo dlya sil'noi volny uplotneniya (plotnost' gaza v obolochke mnogo bol'she, chem v oblasti N I).

Usloviya na ionizacionnom fronte takzhe opredelyayutsya (6.29), no uzhe s drugimi oboznacheniyami parametrov. Zdes' neizvestny plotnost' na vnutrennei granice obolochki $\rho'_1 = \rho'_2 R'_2(\lambda_i)$ i sootvetstvuyushaya skorost' gaza $V'_1(\lambda_i)\sqrt{\frac{\Re T_2}{\mu_2}}$ . Teper' vazhno takzhe uchest', chto hotya T₁ i malo po sravneniyu s T₂, no skorost' vtekaniya gaza v oblast' fronta ionizacionnogo razryva

$v'_1(\lambda_i) = \lambda_i\sqrt{\frac{\Re T_2}{\mu_2}}[1 - V'_1(\lambda_i)]$ (6.53)

takzhe mala. Poetomu sleduet ispol'zovat' polnoe sootnoshenie (6.29):

$\begin{array}{l} R'_1(\lambda_i) = \frac{1 - V_2(\lambda_i)}{1 - V'_1(\lambda_i)} = \frac{1}{2}\left(1 + \frac{\mu_2 T_1}{\mu_1 T_2} \frac{1}{\lambda_i^2 [1 - V_i(\lambda_i)]^2} + \right.\\ \left.+ \sqrt{\left(1 + \frac{\mu_2 T_1}{\mu_1 T_2} \frac{1}{\lambda_i^2 [1 - V'_1(\lambda_i)]^2}\right)^2} - \frac{4}{\lambda_i^2 [1 - V'_1(\lambda_i)]^2} \right). \end{array}$ (6.54)

Krome togo, soglasno (6.48), velichina λ_i[1 - V₂(λ_i)] schitaetsya zadannoi usloviem (6.41). Itak, my poluchili eshe tri sootnosheniya dlya opredeleniya chetyreh velichin R'₁(λ_i), V'₁(λ_i), V₂(λ_i) i λ_i. Poskol'ku neobhodimo naiti svyaz' mezhdu λ_i i λ_s, nuzhny eshe dva usloviya. Ochevidno, chto oni sleduyut iz uravnenii avtomodel'nogo dvizheniya gaza v szhatoi obolochke N I.

Resheniya etih uravnenii ochen' prosty dlya ploskih ionizacionnyh frontov (t. e. v sluchae (6.45)). Takoe reshenie mozhno schitat' priblizhenno pravil'nym, esli otnositel'naya tolshina obolochki mala. Togda iz (6.45) imeem

$\begin{array}{l} R'_2(\lambda_s) = R'_1(\lambda_i), \\ V'_2(\lambda_s) = V'_1(\lambda_i)\frac{\lambda_i}{\lambda_s}. \end{array}$ (6.55)

Uravneniya (6.55) i zamykayut polnuyu sistemu uravnenii (6.48), (6.52), (6.54). Reshenie etoi sistemy i v obshem sluchae neslozhno, no ego mozhno eshe bolee uprostit', rassmotrev sluchai, kogda plotnost' gaza v szhatoi obolochke bol'she i plotnosti v H I i plotnosti v N II. Togda R'₂(λ_s) = R'₁(λ_i) ≫ 1 i sootnoshenie (6.54) uproshaetsya:

$R'_1(\lambda_i) = \frac{1 - V_2(\lambda_i)}{1 - V'_1(\lambda_i)} \approx \frac{\mu_2 T_1}{\mu_1 T_2}\frac{1}{\lambda_i^2 [1 - V'_1(\lambda_i)]^2}.$ (6.56)

Oboznachaya cherez A i α velichiny

$\begin{array}{l} A = \lambda_i [1 - V_2(\lambda_i)] \\ \alpha = \frac{\mu_2 T_1}{\mu_1 T_2} , \end{array}$ (6.57)

kotorye soglasno usloviyu schitayutsya zadannymi, i polagaya α ≪ 1, nahodim reshenie v bezrazmernyh peremennyh:

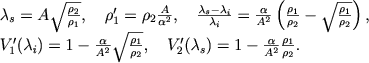
$\begin{array}{l} \lambda_s = A\sqrt{\frac{\rho_2}{\rho_1}}, \quad \rho'_1 = \rho_2 \frac{A}{\alpha^2}, \quad \frac{\lambda_s - \lambda_i}{\lambda_i} = \frac{\alpha}{A^2}\left(\frac{\rho_1}{\rho_2} - \sqrt{\frac{\rho_1}{\rho_2}}\right), \\ V'_1(\lambda_i) = 1 - \frac{\alpha}{A^2}\sqrt{\frac{\rho_1}{\rho_2}}, \quad V'_2(\lambda_s) = 1 - \frac{\alpha}{A^2}\frac{\rho_1}{\rho_2}. \end{array}$ (6.58)

Perehodya k razmernym peremennym, imeem dlya skorosti dvizheniya udarnoi volny v zone N I (po sushestvu, dlya skorosti dvizheniya vsei obolochki):

$v_{\mbox{ud}} \approx \frac{\mu_2 m_H J}{\sqrt{\rho_1\rho_2}}.$ (6.59)

Plotnost' gaza N I vnutri obolochki velika i opredelyaetsya kvadratom plotnosti potoka ionizuyushih kvantov:

$\rho'_1 \approx \frac{\mu_1\mu_2^2 m_H^2 J^2}{\rho_2\Re T_1}.$ (6.60)

Otnositel'naya tolshina obolochki sootvetstvenno mala:

$\frac{\lambda_s - \lambda_i}{\lambda_i} \approx \frac{\rho_2}{\rho_1}\left(\frac{\rho_1}{\rho_2} - \sqrt{\frac{\rho_1}{\rho_2}}\right).$ (6.61)

Eti prostye rezul'taty podtverzhdayutsya i chislennym raschetom bolee polnoi zadachi.

Dlya sravneniya privedem rezul'taty Laskera [24], poluchennye pri chislennom integrirovanii uravnenii dvizheniya (ris. 23). Vidny oblasti szhatoi obolochki s sil'noi udarnoi volnoi uplotneniya, za kotoroi sleduet ionizacionnaya volna razrezheniya. Tolshina szhatoi obolochki v zone N I, deistvitel'no, otnositel'no mala. Pravda, nablyudaemye tolshiny szhatyh obolochek obychno sushestvenno bol'she i mogut byt' sravnimy s ih radiusom. Vozmozhno, chto sushestvenna rol' magnitnogo polya [24], vliyanie kotorogo, kstati, mozhno uchest' takzhe v ramkah avtomodel'nogo metoda.

Ionizacionnye fronty sleduet otlichat' ot ionizuyushih udarnyh voln. U ionizacionnyh frontov menyaetsya sostoyanie ionizacii blagodarya prohozhdeniyu cherez sredu potoka vneshnih kvantov s energiei, bol'shei poroga ionizacii, a u ionizuyushih udarnyh voln vnutri fronta menyaetsya sostoyanie ionizacii prosto kak sledstvie nagrevaniya gaza za frontom udarnoi volny. Takie udarnye volny bol'shoi intensivnosti, rasprostranyayushiesya v neionizovannom gaze (naprimer, v zemnoi atmosfere), ostavlyayut za soboi oblast' zametnoi ionizacii. Hotya v astrofizike, veroyatno, vstrechayutsya podobnye ionizuyushie udarnye volny, no osobyi interes predstavlyaet issledovanie etih voln dlya prikladnyh zadach geofiziki i poetomu my zdes' eti volny rassmatrivat' ne budem.

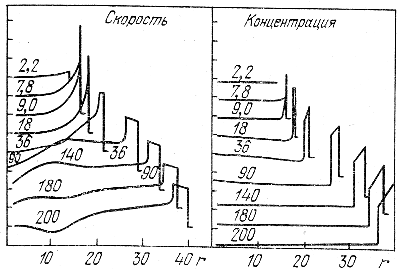
Ris. 23. Skorost' (sleva) i koncentraciya (sprava) v sluchae dvizhushegosya ionizacionnogo fronta, pered kotorym rasprostranyaetsya v zone N I udarnaya volna.
Razlichnye krivye sootvetstvuyut raznym momentam vremeni posle nachala rasshireniya. Chisla pokazyvayut eto vremya v edinicah 10⁴ let. Edinica skorosti - 3,2 km/sek, edinica koncentracii - 6,4 sm^-3 rasstoyanie v ps.

Upomyanem tol'ko o nekotoryh issledovaniyah dvizheniya ionizuyushih udarnyh voln v srede s magnitnym polem. Obychno v astrofizike prinimaetsya uslovie "vmorozhennosti" magnitnogo polya v veshestvo, kogda elektroprovodnost' gaza schitaetsya ochen' bol'shoi. Teoriya udarnyh voln s magnitnym polem v usloviyah polnoi "vmorozhennosti" magnitnogo polya v veshestvo izlagalas' primenitel'no k astrofizicheskim zadacham v knigah [4, 5].

Odnako uslovie "vmorozhennosti" magnitnyh silovyh linii mozhet narushat'sya v oblasti ionizacionnyh razryvov i ionizuyushih udarnyh voln. V chastnosti, esli schitat', chto gaz polnost'yu neitralen pered frontom ionizuyushei udarnoi volny i sil'no ionizovan za ee frontom, to na fronte takoi udarnoi volny imeet mesto skachok elektroprovodnosti ot nulya do ochen' bol'shoi velichiny. Sledovatel'no, na fronte takoi volny menyaetsya uslovie "vmorozhennosti" - ot ee polnogo otsutstviya do pochti polnoi "prikleennosti" magnitnyh silovyh linii k dvizheniyu veshestva.

Takie ionizuyushie udarnye volny so skachkom elektroprovodnosti byli rassmotreny v ryade rabot A. A. Barmina, A. G. Kulikovskogo, G. A. Lyubimova (sm. [25, 26]). Osnovnoe vnimanie udelyalos' issledovaniyu ustoichivosti podobnyh voln. V srede s magnitnym polem est' bol'shoe chislo razlichnyh voln i poetomu sleduet uchityvat' vozmozhnost' raspada razryva na lyubye kombinacii lineinyh voln. V rabote [26] rassmatrivalas' i avtomodel'naya zadacha o dvizhenii ionizuyushei udarnoi volny v parallel'nom frontu magnitnom pole pod deistviem porshnya, dvizhushegosya s postoyannoi skorost'yu.

V astrofizicheskih ionizacionnyh razryvah tozhe est' skachki elektroprovodnosti, no rol' etih skachkov ne tak velika. Delo v tom, chto dazhe v oblasti neionizovannogo vodoroda est' zametnaya koncentraciya elektronov ot ionizacii drugih elementov, i poetomu elektroprovodnost' dostatochno velika i pered ionizacionnym frontom. "Vmorozhennost'" magnitnyh silovyh linii imeet mesto kak pered ionizacionnym frontom, tak i za nim. Krome togo, v real'nyh ionizacionnyh razryvah v mezhzvezdnom prostranstve imeet mesto ne szhatie, a razrezhenie veshestva, i, sledovatel'no, ne usilenie, a, naoborot, oslablenie magnitnogo polya. Konechno, polnaya teoriya ionizacionnyh razryvov dolzhna uchityvat' rol' magnitnogo polya, no poka eto eshe ne sdelano.

Krome ionizuyushih udarnyh voln i ionizacionnyh razryvov vozmozhny i rekombinacionnye udarnye volny i razryvy. Zdes' dvizhushei siloi yavlyaetsya energiya, vydelyayushayasya pri rekombinacii gaza. Takie udarnye volny analogichny volnam goreniya, horosho izvestnym v gazodinamike. Svoistva rekombinacionnyh razryvov v astrofizike izuchalis', naprimer, v rabote [27]. No i ionizacionnye fronty po svoim svoistvam neskol'ko napominayut volny goreniya, poskol'ku i zdes' dvizhushei siloi yavlyaetsya vydelenie energii vnutri fronta volny.

<< § 6.1 Uravneniya avtomodel'nogo dvizheniya kosmicheskogo gaza | Oglavlenie | § 6.3 Avtomodel'nye dvizheniya v zvezdah i protozvezdah >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

$\rho_1 v_1 = \rho_2 v_2,$	(6.27)
$\rho_1\left(v_1^2 + \frac{\Re T_1}{\mu_1}\right) = \rho_2\left(v_2^2 + \frac{\Re T_2}{\mu_2}\right),$	(6.28)

$\frac{\rho_2}{\rho_1} = \frac{v_1}{v_2} \approx \frac{\mu_2 v_1^2}{\Re T_2},$	(6.30)
$\frac{\rho_2}{\rho_1} = \frac{v_1}{v_2} = 1 + \frac{\Re T_2}{\mu_2 v_1^2}.$	(6.31)