Astronet > Razmernosti i podobie astrofizicheskih velichin

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 7.1 Sistema uravnenii i parametry zvezdnyh siste | Oglavlenie | § 7.3 Volny plotnosti vo vrashayushihsya galaktikah >>

§ 7.2 Vremya relaksacii zvezdnyh sistem

Vazhneishei problemoi dinamiki zvezdnyh -sistem yavlyaetsya opredelenie ee harakternogo vremeni relaksaciya, kotoruyu my budem oboznachat' cherez t_E. Eto opredelenie svyazano s razlichiem mezhdu regulyarnymi i irregulyarnymi silami v zvezdnyh sistemah. Obshaya teoriya izlagalas' vo mnogih rabotah i knigah (sm., naprimer, [3]). Zdes' my ogranichimsya lish' prostoi traktovkoi, osnovannoi la teorii analiza razmernostei i kachestvennyh soobrazheniyah

Sily, deistvuyushie na dvizhenie zvezd v zvezdnyh sistemah, mozhno razdelit' na dva tipa. Regulyarnye sily voznikayut ot deistviya obshego, tak nazyvaemogo samosoglasovannogo, gravitacionnogo polya vsei sistemy. Pod deistviem etoi sily zvezda opisyvaet v sisteme nekotoruyu bolee ili menee pravil'nuyu orbitu. Naprimer, vo vrashayusheisya spiral'noi galaktike zvezdy opisyvayut pochti krugovye orbity pod deistviem regulyarnogo gravitacionnogo polya. V kvazisfericheokih zvezdnyh sistemah tozhe imeyutsya regulyarnye orbity, no oni mogut byt' sushestvenno bolee elliptichnymi. Harakternyi period dvizheniya zvezd pod deistviem regulyarnyh sil nazyvaetsya vremenem peresecheniya P v skopleniyah ili periodom obrasheniya 2π / Ω vo vrashayushihsya galaktikah. Soderzhanie predydushego paragrafa est', po sushestvu, opredelenie harakternogo vremeni regulyarnyh sil.

Regulyarnye sily opredelyayut harakternuyu velichinu regulyarnyh skorostei, primerno ravnuyu v_R ≈ R/P ili v_R = RΩ dlya skoplenii ili vrashayushihsya galaktik sootvetstvenno. Poetomu mozhno napisat'

$v_{R}^{2} = \frac{1}{\Pi} \frac{G \mathcal{M}}{R}$ (7.18)

esli vospl'zovat'sya opredeleniyami (7.8) i (7.9). Mozhno opredelit' i velichinu bezrazmernogo kompleksa Π, esli vospol'zovat'sya teoremoi viriala ili kakimi-nibud' drugimi soobrazheniyami. Naprimer, dlya strogo vrashatel'nogo dvizheniya sila gravitacionnogo prityazheniya na krayu sistemy $(G \mathcal{M} / R^{2})$ dolzhna ravnyat'sya cenrobezhnoi sile v_R² / R. Zdes' Π = 1. Odnako iz teoremy viriala parametr Π imeet bol'shee znachenie, strogo govorya zavisyashee ot geometrii sistemy. Dlya odnorodnyh sfericheskih sistem gravitacionnaya potencial'naya energiya

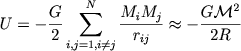
$U = -\frac{G}{2} \sum\limits_{i, j = 1, i \ne j}^{N} \frac{M_{i}M_{j}}{r_{ij}} \approx - \frac{G \mathcal{M}^{2}}{2R}$ (7.19)

i kineticheskaya energiya

$W = \sum\limits_{i=1}^{N} \frac{1}{2} M_{i} v_{i}^{2} \approx \frac{1}{2} \mathcal{M} v_{R}^{2}$ (7.20)

Iz teoremy viriala sleduet, chto &Pi = 2, t.e

$v_{R}^{2} = \frac{G \mathcal{M}}{2R}$ (7.21)

Etim sootnosheniem my i budem pol'zovat'sya

Teper' pereidem k analizu irregulyarnyh sil ,i skorostei. Oni svyazany so sblizheniyami otdel'nyh zvezd, pri kotoryh skorosti etih zvezd ispytyvayut znachitel'nye izmeneniya. Izmenenie skorosti pri sblizheniyah imeet stohasticheskii harakter i poetomu zameten lish' summarnyi effekt mnogih sblizhenii. Deistvie irregulyarnyh sil opisyvaetsya harakternym vremenem relaksacii t_E, t. e. promezhutkom vremeni, v techenie kotorogo zametno izmenitsya skorost' zvezdy pod deistviem stohasticheskih sblizhenii, libo sootvetstvuyushei dlinoi svobodnogo probega, oboznachaemoi v dal'neishem cherez l_E.

Elementarnoe opredelenie l_E mozhno poluchit' sleduyushim obrazom. Ochevidno, chto eta velichina ravna

$l_{E} \approx (\overline{n} \pi s^{2} \Lambda)^{-1}$ (7.22)

gde $\overline{n}$ , po-prezhnemu, koncentraciya zvezd, π s² - effektivnoe sechenie zvezdnyh sblizhenii, Λ - kulonovskii logarifm, uchityvayushii vklad dalekih sblizhenii. Dlya opredeleniya parametra s - pricel'nogo rasstoyaniya sblizheniya - postupim sleduyushim obrazom. Budem schitat' sblizhenie effektivnym, esli pri etom skorost' vozrastet ne menee, chem na nekotoruyu zadannuyu velichinu v_i. Priravnivaya prirashenie kineticheskoi energii zvezdy so srednei massoi $\frac{1}{2} \overline{M} v^{2}_{i}$ potencial'noi energii sblizheniya na pricel'nom rasstoyanii GM² / s poluchim

$s = \frac{2GM}{v_{i}^{2}}$ (7.23)

Podstavlyaya v (7.22) takzhe $n = \overline{n} = \frac{3N}{4 \pi R^{3}}$ i uchityvaya (7.21), gde $\mathcal{M} = N \overline{M}$ , poluchim

$l_{E} = \left( \frac{v_{i}}{v_{R}} \right)^{4} \frac{RN}{12 \Lambda}$ (7.24)

V kvazisfericheskih nevrashayushihsya sistemah irregulyarnye sily okazyvayut zametnoe deistvie togda, kogda skorosti v_i okazyvayutsya sravnimymi s v_R. Krome togo, kak pokazyvaet raschet, v takih sistemah s bol'shim chislom chastic kulonovskii logarifm v pervom priblizhenii raven Λ = ln N [3]. Takim obrazom,

$\frac{l_{E}}{R} \approx \frac{N}{12 \ln N}$ (7.25)

Chislennoyi koefficient 1 / 12 neskol'ko izmenyaetsya pri bolee rafinirovannom raschete.

V ploskih vrashayushihsya galaktikah effekt irregulyarnyh sil privodit k men'shemu izmeneniyu skorostei, chem velichina v_R, kotoraya zdes' sootvetstvuet lineinoi skorosti vrasheniya. Pod v_I, tut sleduet ponimat' dispersiyu pekulyarnyh skorostei zvezd. Nablyudatel'nye dannye pokazyvayut, chto v bystro vrashayushihsya ploskih galaktikah otnoshenie v_I / v_R ochen' malo, veroyatno, men'she 1/10. Poetomu dlya spiral'nyh galaktik otnoshenie l_E / R dolzhno byt' poryadka 10^-5 N / ln N. No eta velichina vse zhe na mnogo poryadkov bol'she edinicy, tak kak N ≈ 10¹⁰ - 10¹² .

Velichina dliny svobodnogo probega zametno umen'shaetsya pri uchete neodnorodnosti zvezdnoi sistemy. Eto mozhno uvidet' srazu zhe iz formul (7.22) i (7.23). Dopustim, chto v zvezdnoi sisteme est' bol'shie fluktuacii plotnosti chisla zvezd, t. e. sistema neodnorodna. Pust' massa kazhdoi fluktuacii poryadka M_f (M_f » $\overline{M}$ ) i primem, chto chislo takih fluktuacii na edinicu ob'ema est' n_f. Dlya ocenki dliny svobodnogo probega takzhe mozhno ispol'zovat' formulu (7.23), zameniv v nei $\overline{M}$ na M_f. V rezul'tate poluchim dlya dliny svobodnogo probega

$l_{E} = \frac{v_{I}^{4}}{4 \pi n_{\Phi}(GM_{\Phi})^{2}} \approx \frac{v_{I}^{4}}{4 \pi \overline{n}(G\overline{M})^{2}} \frac{\overline{M}}{M_{\Phi}}$ (7.26)

Zdes' prinyato, chto srednyaya plotnost' massy vo fluktuaciyah, t. e. velichina n_fM_f, ne slishkom sil'no otlichaetsya ot srednei plotnosti zvezd voobshe, t. e. ot velichiny $\overline{nM}$ . Krome togo, pri rasseyanii zvezd na bol'shih fluktuaciyah kulonovekii logarifm Λ poryadka edinicy. Iz (7.26) srazu vidno, chto v neodnorodnoi sisteme, v kotoroi zvezdy raspredeleny v vide sovokupnosti zvezdnyh oblakov, kazhdoe iz kotoryh soderzhit ochen' bol'shoe chislo zvezd (M_f » $\overline{M}$ ), dlina svobodnogo probega umen'shaetsya ochen' sil'no. Esli by vsya galaktika sostoyala yaz zvezdnyh skoplenii s massoi poryadka 10⁵ maos Solnca, to mozhno bylo by poluchit' dlinu svobodnogo probega, sravnimuyu s ee razmerom. Odnako na samom dele zvezdnyi fon v galaktikah sushestvenno odnorodnee i zdes' vsegda l_E » R.

Pri chislennom modelirovanii chasto rassmatrivayut ideal'no ploskuyu sistemu; schitaetsya, chto vse zvezdy dvizhutsya v odnoi ploskosti. Poetomu sootnoshenie mezhdu dlinoi svobodnogo probega i R okazyvaetsya sushestvenno drugim [4]. Vmesto (7.22) imeem

$l_{E} = (\overline{n_{S}}2s \Lambda)^{-1}$ (7.27)

poskol'ku effektivnoe sechenie vzaimodeistviya predstavlyaet soboi otrezok v ploskosti dvizheniya, ravnyi 2s, gde s po-prezhnemu, pricel'noe rasstoyanie. Polagaya $\overline{n_{s}} = \frac{N}{\pi R^{2}}$ i uchityvaya (7.23) i (7.21), poluchim

$l_{E} = \left( \frac{v_{I}}{v_{R}} \right)^{2} \frac{\pi R}{8 \Lambda} = \left( \frac{v_{I}}{v_{R}} \right)^{2} \frac{\pi R}{8 \ln N}$ (7.28)

Zdes' l_E « R, dazhe esli v_I sravnimo s v_R- Opredelenie (7.28) dlya dliny svobodnogo probega primenimo i k fizicheski real'nym sistemam, esli parametr s iz (7.23) sravnim ili men'she tolshiny sistemy (zdes' v_I - dispersiya skorostei v ploskosti dvizheniya).

Harakternoe vremya relaksacii opredelyaetsya kak otnoshenie dliny svobodnogo probega k srednei skorosti dvizheniya zvezd. Odnako my opredelim etu velichinu drugim sposobom, ispol'zuya soobrazheniya analiza razmernostei. Eto sdelano v knige [5], no my vospol'zuemsya drugim metodom.

Prezhde vsego vydelim osnovnye opredelyayushie parametry. Irregulyarnye sily, privodyashie k relaksacii sistemy, zavisyat ot postoyannoi G, maos otdel'nyh zvezd, t. e. $\overline{M}$ , koncentracii zvezd $\overline{n}$ i nekotoroi srednei skorosti chastic, kotoruyu my poka oboznachim cherez v ′. Iskomaya velichina t_E imeet razmernost' vremeni. Iz etih opredelyayushih parametrov sostavim matricu razmernosti

$\begin{matrix} \, & [G] & [\overline{M}] & [\overline{n}] & [v^{\prime}] & [t_{E}] \\ \mbox{g} & -1 & 1 & 0 & 0 & 0 \\ \mbox{sm} & 3 & 0 & -3 & 1 & 0 \\ \mbox{sek}&-2 & 0 & 0 & -1 &1 \end{matrix}$

Rang matricy raven trem, t. e. est' dva nezavisimyh bezrazmernyh kompleksa. Mozhno ih vybrat' proizvol'nym obrazom, ispol'zuya te ili inye fizicheskie soobrazheniya. Vo-pervyh, sostavim eti kompleksy tak, chtoby t_E vhodilo by v nih v pervoi stepeni. Vo-vtoryh, odin iz kompleksov sostavim bez skorosti v ′. Togda poluchim

$\Pi_{1} = t_{E} (G \overline{M} \overline{n})^{1/2}$ (7.29)

Vo vtorom komplekse ostavim vse opredelyayushie parametry, no potrebuem, chtoby velichina t_E byla by obratno proporcional'na koncentracii zvezd, inymi slovami, v etot kompleks vhodilo by proizvedenie $t_{E} \overline{n}$ . Togda imeem

$\Pi_{2} = t_{E} \overline{n} (G \overline{M})^{2} (v^{\prime})^{3}$ (7.30)

V takom opredelenii mozhet zaklyuchat'sya nekotoryi proizvol, no, kak my uvidim nizhe, etot vybor deistvitel'no opravdan. Sopostavim bezrazmernyi kompleks (7.29) s sootnosheniem (7.13). Otsyuda srazu sleduet, chto esli t_E poryadka vremeni peresecheniya P, to Π₁ - poryadka edinicy. No my uzhe znaem, chto u sistem s bol'shim chislom zvezd dlina svobodnogo probega mnogo bol'she harakternyh razmerov i, sledovatel'no, vremya relaksacii dolzhno byt' mnogo bol'she vremeni peresecheniya. Poetomu v takih sistemah Π₁ » 1, i etot bezrazmernyi kompleks ne mozhet harakterizovat' opredelenie vremeni relaksacii.

Ostaetsya bezrazmernyi kompleks (7.30), otkuda sleduet

$t_{E} \approx \frac{\Pi^{2} (v^{\prime})^{3}}{\overline{n}(G \overline{M})^{2}}$ (7.31)

gde Π₂ ne mozhet ochen' sil'no otlichat'sya ot edinicy. Kak uzhe otmechalos', zdes' est' nekotoryi proizvol, svyazannyi s tem, chto my schitali $t_{E} \sim \overline{n}^{-1}$ . No eto ochevidno, tak kak chem bol'she koncentraciya zvezd, tem men'she i vremya relaksacii. Krome togo, zdes' uchteno, chto relaksaciya proishodit pri vzaimodeistvii otdel'nyh zvezd, t. e. kak by pri ih "stolknoveniyah". Chastota stolknovenii vsegda obratno proporcional'na koncentracii.

Sopostavlyaya (7.31) s (7.24) i (7.25), a takzhe uchityvaya opredelenie vremeni peresecheniya (7.13), mozhno poluchit' sootnoshenie

$\frac{t_{E}}{P} \approx \frac{t_{E}}{R} \approx \frac{N}{12 \ln N}$ (7.32)

pri sootvetstvuyushem vybore chislennogo znacheniya bezrazmernogo kompleksa Π₂ (proporcional'nogo (ln N)^-1) i uslovii v ′ = v_R iz (7.21). Eto sootnoshenie my i primem za opredelenie harakternogo vremeni relaksacii dlya kvazisfericheskih nevrashayushihsya skoplenii.

Harakternoe vremya relaksacii v ploskih spiral'nyh galaktikah svyazano s dlinoi svobodnogo probega (7.26) podobnym sootnosheniem, esli schitat' skorost' v ′ v (7.31) ravnoi skorosti v_I v (7.24). Vmesto vremeni peresecheniya zdes' sleduet uchest' period obrasheniya. Poluchaem sleduyushuyu formulu, uchityvayushuyu takzhe nalichie fluktuacii massy:

$t_{E} \approx \left( \frac{v_{I}}{v_{R}} \right)^{3} \frac{N}{\Omega} \frac{\overline{M}}{M_{\Phi}}$ (7.33)

Zdes' pod v_I, sleduet ponimat' pekulyarnuyu skorost' zvezd, a v_R, est' lineinaya skorost' vrasheniya galaktiki. Esli syuda podstavit' v_R ≈ R Ω , a vmesto N vvesti srednyuyu poverhnostnuyu koncentraciyu zvezd $\overline{n}$ , to poluchim sleduyushee sootnoshenie

$t_{E} \approx \frac{v^{3}_{I} \overline{n_{S}}}{R \Omega^{4}} \frac{\overline{M}}{M_{\Phi}}$ (7.34)

Etu formulu mozhno primenyat' dlya ocenki relaksacii zvezd raznogo tipa v galaktikah.

Rezyumiruya vse skazannoe o vremeni relaksacii zvezdnyh sistem, mozhno sdelat' sleduyushii obshii vyvod. V kvazisfericheskih nevrashayushihsya zvezdnyh skopleniyah, sostoyashih iz soten (do tysyachi) zvezd, harakternoe vremya relaksacii sravnimo so vremenem peresecheniya zvezdoi diametra skopleniya. Takie sistemy bystro relaksiruyut i vse vremya nahodyatsya v kvaziravnozesnom sostoyanii. Kvazisfericheskie nevrashayushiesya sistemy, sostoyashie iz soten tysyach zvezd (sharovye skopleniya), imeyut bol'shoe vremya relaksacii, mnogo bol'shee, chem vremya peresecheniya. Vprochem, za dostatochno bol'shoi promezhutok vremeni i eti sistemy uspevayut dostignut' kvaziravnovesnogo sostoyaniya.

V spiral'nyh ploskih galaktikah, sostoyashih iz soten milliardov zvezd, vremya relaksacii pri sblizheniyah otdel'nyh zvezd ochen' veliko i ne mozhet privesti k zametnomu pereraspredeleniyu skorostei zvezd. Zdes' net poetomu i kvaziravnovesnogo sostoyaniya vsei sistemy. Odnako opredelennoe pereraspredelenie energii vse zhe imeet mesto blagodarya kollektivnym processam v takih sistemah.

Evolyuciya kvazisfericheskih nevrashayushihsya skoplenii s N ≈ 10²-10⁵ i ploskih spiral'nyh galaktik s N ≈ 10¹⁰-10¹² principial'no razlichna. V skopleniyah evolyuciya privodit k vyletu zvezd iz skopleniya, a v ploskih vrashayushihsya galaktikah evolyuciya svyazana s vozniknoveniem voln plotnosti - spiral'nyh rukavov.

Probleme vyleta zvezd iz skopleniya bylo posvyasheno mnogo rabot, nachinaya s pervoi raboty V. A. Ambarcumyayaa [6] (sm. takzhe [3]).

V naibolee prostoi postanovke zadacha rascheta skorosti vyleta zvezd iz skopleniya vyglyadit sleduyushim obrazom. Dopustim, chto za vremya, ravnoe vremeni relaksacii t_E, v zvezdnoi sisteme ustanavlivaetsya maksvellovskoe raspredelenie skorostei so srednei harakternoi skorost'yu (7.21). Pri etom nekotoraya chast' zvezd priobretaet skorost', bol'shuyu parabolicheskoi:

$v_{\infty}^{2} = \frac{2G \mathcal{M}}{R} = 4v_{M}^{2}$ (7.35)

Esli schitat', chto pri v > v_∞ raspredelenie skorostei maksvellovskoe, to otnositel'noe chislo zvezd so skorostyami, bol'shimi parabolicheskoi ravno [6]

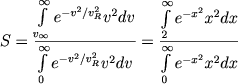
$S = \frac{\int\limits_{v_{\infty}}^{\infty} e^{-v^{2}/v_{R}^{2}}v^{2}dv}{\int\limits_{0}^{\infty} e^{-v^{2}/v_{R}^{2}}v^{2}dv} = \frac{\int\limits_{2}^{\infty} e^{-x^{2}}x^{2}dx}{\int\limits_{0}^{\infty} e^{-x^{2}}x^{2}dx}$ (7.36)

Zvezdy so skorostyami, bol'shimi parabolicheskoi, pokidayut skoplenie i poetomu mozhno schitat', chto za vremya odnoi relaksacii skoplenie teryaet 0,74% ot polnogo chisla zvezd.

Bolee podrobnyi analiz dolzhen uchityvat', chto harakternoe vremya relaksacii razlichno dlya zvezd raznoi massy, i poetomu skoplenie teryaet po-raznomu legkie i tyazhelye zvezdy. Chandracekarom [3] bylo pokazano, chto esli predpolozhit', chto zvezdy raznoi massy raspredeleny ravnomerno po ob'emu skopleniya, to v pervuyu ochered' vyletayut zvezdy s massoi okolo $0.4 \overline{M}$ , prichem za srednee vremya relaksacii vyletayut 3-4% ot polnogo chisla takih zvezd. Zvezdy s massoi okolo $0.1 \overline{M}$ vyletayut s takoi zhe skorost'yu, chto i zvezdy so srednei massoi $\overline{M}$ , t. e. ih vyletaet 0,74% za odno srednee vremya relaksacii. S drugoi storony, zvezdy ochen' malyh ( $0.05 \overline{M}$ ) ili bol'shih ( $1.4 \overline{M}$ ) mass vyletayut .medlenno - za odno vremya relaksacii teryaetsya 0,1-0,2% ot polnogo chisla takih zvezd.

Vprochem, predpolozhenie o ravnomernosti raspredeleniya zvezd po ob'emu skopleniya ili hotya by o podobnosti takogo raspredeleniya dlya zvezd raznyh mass, veroyatno, daleko ot real'nosti. Zvezdy bol'shih mass dolzhny koncentrirovat'sya k central'noi chasti skopleniya, a legkie zvezdy chashe vstrechayutsya na periferii. V rezul'tate skorosti poter' zvezd raznoi massy vyravnivayutsya. Ocenki etogo yavleniya, sdelannye raznymi avtorami [7, 8, 9], rashodyatsya i poetomu dlya prostoty mozhno ogranichit'sya pervym usloviem - skoplenie teryaet 0,7-0,8% ot polnogo chisla zvezd za odno vremya relaksacii.

Poskol'ku vyletayushie zvezdy unosyat s soboi polozhitel'nuyu energiyu, to absolyutnoe znachenie otricatel'noi polnoi energii skopleniya vse vremya rastet (primerno na 0,52% za vremya relaksacii) i skoplenie stanovitsya so vremenem plotnee i kompaktnee. Vozmozhno, chto pri etom proishodit nekotoroe obogashenie skopleniya tyazhelymi zvezdami.

<< § 7.1 Sistema uravnenii i parametry zvezdnyh siste | Oglavlenie | § 7.3 Volny plotnosti vo vrashayushihsya galaktikah >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce