Astronet > Razmernosti i podobie astrofizicheskih velichin

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 7.2 Vremya relaksacii zvezdnyh sistem | Oglavlenie | § 7.4 Chislennoe modelirovanie evolyucii zvezdnyh skoplenii >>

§ 7.3 Volny plotnosti vo vrashayushihsya galaktikah

V etoi glave my rassmatrivaem gravitiruyushie zvezdnye sistemy, sostoyashie iz nestalkivayushihsya mezhdu soboi material'nyh tochek - zvezd. No dlya togo chtoby poyasnit', chto takoe volny plotnosti v zvezdnyh sistemah, udobnee nachat' s sistemy, sostoyashei iz gravitiruyushego gaza.

Napomnim izvestnoe dispersionnoe sootnoshenie dlya zvukovyh voln:

$\omega = \frac{2 \pi v_{s}}{\lambda} = v_{s} k$ (7.37)

gde ω - chastota volny, v_s - skorost' zvuka, λ - dlina volny, k - volnovoe chislo. Zvukovaya volna sostoit iz razrezhenii i uplotnenii gaza. Kolebaniya gaza v volne opredelyayutsya tem, chto uprugaya sila edinicy ob'ema, ravnaya, po opredeleniyu, velichine ρ_gω²x, gde x - smeshenie chastic, ρ_g - srednyaya plotnost' gaza, sozdaet izbytok sily gazovogo davleniya v uplotneniyah volny. Etot izbytok proporcionalen velichine p (x / λ²), gde p ∼ ρ_gT ∼ρ_gv_s² - srednee davlenie. Formula (7.37) spravedliva lish' v sluchae zvuka s maloi dlinoi volny. Esli pereiti k volnam bol'shei dliny, to sleduet uchityvat' effekty samogravitacii. V oblasti szhatiya gaz uplotnyaetsya, chto privodit k poyavleniyu dopolnitel'noi sily vzaimnogo gravitacionnogo prityazheniya, prepyatstvuyushei posleduyushemu rasshireniyu. Eto v svoyu ochered' ekvivalentno poyavleniyu "otricatel'nogo" davleniya v volne. Velichinu sootvetstvuyushego vklada v upruguyu silu mozhno poluchit', sostaviv iz parametrov, harakterizuyushih effekt samogravitacii, t. e. velichin G, ρ i λ, velichinu s razmernost'yu ρ_gω². Netrudno ubedit'sya, chto takoi kombinaciei est' proizvedenie G ρ_g². Dobavlyaya syuda sleduyushii iz tochnoi teorii mnozhitel' 4π, poluchim dispersionnoe sootnoshenie, opredelyayushee chastotu voln "tyazhelogo zvuka", t. e. zvukovyh voln s uchetom samogravitacii

$\omega^{2} = v_{s}^{2}k^{2} - 4 \pi G \rho_{g}$ (7.38)

Iz etoi formuly bylo polucheno mnogo sledstvii. Naprimer, otsyuda sleduet izvestnyi kriterii neustoichivosti Dzhinsa. U voln "tyazhelogo zvuka" s bol'shoi dlinoi "otricatel'noe davlenie" samogravitacii bol'she obychnogo gazovogo davleniya, t. e. v_s²k² < 4 πG ρ_g. V etom sluchae fluktuacii plotnosti v volne okazyvayutsya neustoichivymi i budut neogranichenno szhimat'sya (chto sootvetstvuet usloviyu ω² < 0). Dlina volny neustoichivyh po Dzhinsu vozmushenii

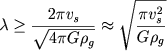
$\lambda \geq \frac{2 \pi v_{s}}{\sqrt{4 \pi G \rho_{g}}} \approx \sqrt{\frac{\pi v_{s}^{2}}{G \rho_{g}}}$ (7.39)

Sootvetstvenno dlya mass fluktuacii, na kotorye raspadaetsya neodnorodnaya sreda, imeem

$M \geq \rho_{g} \lambda^{3} \approx \frac{\pi^{3/2}v_{s}^{3}}{G^{3/2} \rho_{g}^{1/2}}$ (7.40)

K voprosu o sledstviyah neustoichivosti Dzhinsa my vernemsya v gl. 8. Zdes' zhe zametim, chto formula (7.40) mozhet byt' srazu poluchena iz soobrazhenii analiza razmernostei, poskol'ku neustoichivost' sredy po otnosheniyu k raspadu na fluktuacii massoi M dolzhna opredelyat'sya vsego chetyr'mya razmervostnymi opredelyayushimi parametrami, vhodyashimi v formulu (7.40).

A teper' pereidem .k odnorodnoi sisteme, sostoyashei iz zvezd. Zdes' tozhe mogli by voznikat' volny plotnosti, no net ekvivalenta gazovogo davleniya. Poetomu dlya voln plotnosti v odnorodnoi sisteme, sostoyashei iz zvezd, mozhno bylo by primenit' sootnoshenie (7.38) pri v_s = 0. No eto privedet k neustoichivosti vseh voln plotnosti, a sledovatel'no, i k neustoichivosti zvezdnoi sistemy voobshe. Odnako est' dve prichiny, snimayushie etu neustoichivost' i obrazuyushie volny plotnosti v zvezdnyh sistemah.

Vo-pervyh, rol' uprugosti gazovogo davleniya prinimaet na sebya vrashenie zvezdnoi sistemy kak celogo. Dlya poyasneniya etogo effekta budem rassuzhdat' tak, kak eto delaetsya pri analize ustoichivosti vrashatel'nogo dvizheniya zhidkosti (sm. [10]). Pust' zvezdy dvizhutsya vo vrashayusheisya zvezdnoi sisteme po priblizhenno krugovym orbitam. Volny plotnosti, voznikayushie v takoi sisteme, smeshayut ih so svoih orbit. Pust' smeshenie zvezdy otnositel'no ravnovesnoi orbity est' δr. Na ravnovesnoi orbite centrobezhnoe uskorenie v² / r = r Ω²(r) kompensirovalos' siloi prityazheniya etoi zhe zvezdy so storony vsei zvezdnoi sistemy. Posle smesheniya izmenitsya i centrobezhnaya sila, deistvuyushaya na etu zvezdu. Legko ubedit'sya v tom, chto vozniknet uprugaya sila, vozvrashayushaya zvezdu obratno na ravnovesnuyu orbitu, esli ee centrobezhnaya sila na novoi orbite men'she, chem centrobezhnaya sila na ravnovesnyh orbitah na tom zhe rasstoyanii.

Chtoby etot effekt vyrazit' matematicheski, zapishem velichinu centrobezhnoi sily, deistvuyushei na zvezdu, cherez sohranyayushuyusya pri smesheniyah velichinu momenta impul'sa:

$\mathfrak{R} = Mrv = Mr^{2} \Omega(r)$ (7.41)

Otsyuda dlya centrobezhnoi sily imeem

$F_{R} = Mr \Omega^{2} = \frac{\mathfrak{R}^{2}}{Mr^{3}}$ (7.42)

Posle smesheniya na novoi orbite centrobezhnaya sila ravna $\mathfrak{R}^{2}/M \cdot (r + \delta r)^{3}$ . No centrobezhnaya sila na rasstoyanii r + δ r ot centra vrasheniya est'

$F_{R}^{\prime} = \frac{[\mathfrak{R}(r + \delta r)]^{2}}{M(r + \delta r)^{3}} = M(r + \delta r)[\Omega(r + \delta r)]^{2}$ (7.43)

Uslovie ustoichivosti zvezdy na orbite est' F_R < F_R^′ ili

$\frac{\delta \mathfrak{R}^{2}}{Mr^{3}} = \frac{\delta(r^{4} \Omega^{2})}{r^{3}} > 0$ (7.44)

Eshe udobnee eto neravenstvo zapisat' v vide

$\chi^{2}(r) = \frac{1}{r^{3}} \frac{d}{dr} (r^{4} \Omega^{2}) > 0$ (7.45)

Parametr χ(r) nazyvaetsya epiciklicheskoi chastotoi, poskol'ku smeshenie zvezd s krugovyh orbit nazyvayut epiciklami.

Eliciklichnost' dvizheniya zvezd vo vrashayushihsya zvezdnyh sistemah i est' ta uprugaya sila, kotoraya delaet vozmozhnym sushestvovanie voln plotnosti, poskol'ku ono igraet rol' davleniya. Vmesto uravneniya (7.38) teper' poluchaem

$\omega^{2} = \chi^{2} - 4 \pi G \rho_{*}$ (7.46)

gde ρ_* - plotnost' raspredeleniya zvezd. Pravda, iz (7.46) na pervyi vzglyad sleduet, chto voln plotnosti zdes', sobstvenno govorya, net, poskol'ku v pravoi chasti etogo sootnosheniya net dliny volny. Inymi slovami, (7.46) opredelyaet tol'ko nekotoruyu harakternuyu chastotu kolebanii koncentracii zvezd. Na samom dele zavisimost' chastoty a ot dliny volny zdes' est'.

Delo v tom, chto effekt samogravitacii voln plotnosti sushestvenno zavisit ot dispersii skorostei zvezd. Ochevidno, chto esli pekulyarnye skorosti zvezd veliki, to zvezdy bystro ubegayut iz oblasti szhatiya, v volne plotnosti i poetomu effekt samogravitacii voln plotnosti ne uspevaet proyavit'sya. Kriteriem yavlyaetsya sravnenie pekulyarnyh skorostei zvezd, oboznachaemyh cherez v_I, s fazovoi skorost'yu voln plotnosti ω / k. Zamenyaya zdes' ω na χ, poluchim neravenstvo, pri kotorom volny plotnosti sushestvuyut:

$v_{I} \leq \frac{\omega}{k} \approx \frac{\chi}{2 \pi} \lambda$ (7.47)

Bolee strogoe rassmotrenie pozvolyaet zapisat' dispersionnoe sootnoshenie (7.46) v vide

$\omega^{2} = \chi^{2} - 4 \pi G \rho_{*} f \left( \frac{v_{I}k}{\chi} \right)$ (7.48)

gde ρ_* - po-prezhnemu zvezdnaya plotnost', a faktor redukcii f bystro spadaet s rostom argumenta. Pri ne slishkom bol'shih znacheniyah etoi velichiny imeem f ∼ exp(-(v_Ik / χ)²). Takim obrazom, vo vrashayusheisya zvezdnoi sisteme takzhe imeyutsya volny plotnosti, ustoichivye pri malyh dlinah voln (bol'shih k), esli tol'ko dispersiya pekulyarnyh skorostei zvezd ne slishkom mala. Volny s bol'shoi dlinoi mogut byt' neustoichivymi (tipa neustoichivosti Dzhinsa), no zdes' vse volny plotnosti mogut byt' ustoichivymi, esli tol'ko epiciklicheskaya chastota dostatochno velika, tochnee, esli

$\frac{1}{r^{4}} \frac{d}{dr} (r^{4} \Omega^{2}) > 4 \pi G \rho_{*}$ (7.49)

Do sih por my ne uchityvali, chto vrashayushiesya zvezdnye sistemy, kak pravilo, imeyut geometriyu ploskogo diska. V etom sluchae privedennye vyshe sootnosheniya spravedlivy tol'ko do teh por, poka dlina volny plotnosti mnogo men'she tolshiny ploskogo diska galaktiki. Esli zhe rassmatrivayutsya volny plotnosti s dlinoi volny, mnogo bol'shei tolshiny sloya, to vo vseh privedennyh sootnosheniyah sleduet velichinu ρ_*. zamenit' na (1/2)ρ_Sk = (π ρ_S) / λ, gde ρ_S - poverhnostnaya plotnost' zvezd, a k - gorizontal'noe (t. e. raspolozhennoe v ploskosti diska) volnovoe chislo.

Dispersionnoe sootnoshenie dlya koncentricheskih volya plotnosti vo vrashayushemsya diske galaktiki zapisyvaetsya v vide

$\omega^{2} = \chi^{2} - 2 \pi G |k| \rho_{*} f \left( \frac{v_{I}k}{\chi} \right)$ (7.50)

gde faktor f opisyvaetsya slozhnoi funkciei s asimptoticheskimi vyrazheniyami:

$f \left( \frac{v_{I}k}{\chi} \right) = \exp \left( - \frac{v_{I}^{2}k^{2}}{\chi^{2}} \right) \quad (v_{I}k \ll \chi)$ (7.51)

$f \left( \frac{v_{I}k}{\chi} \right) = \left( \frac{2}{\pi} \right)^{1/2} \left( \frac{\chi^{2}}{v_{I}^{2}k^{2}} \right)^{3/2} \quad (v_{I}k \gg \chi)$

Volny plotnosti, opisyvaemye etimi vyrazheniyami, sostoyat iz koncentricheskih kolec razrezhenii i szhatii gaza po vsemu secheniyu diska, rasprostranyayushihsya ot centra galaktiki, esli k > 0, i styagivayushihsya k centru pri k < 0.

Iz formuly (7.50) vytekaet uslovie ustoichivosti zvezdnogo diska po otnosheniyu k volnam plotnosti (sm. [11]). V samom dele, dlya ustoichivosti diska neobhodimo, chtoby dlya vseh vozmozhnyh voln (t. e. dlya lyubyh k] chastota voln plotnosti byla by deistvitel'noi, t. e. ω² > 0. Otsyuda uslovie ustoichivosti

$\chi^{2} > \max \left[ 2 \pi G \rho_{S} |k| f \left( \frac{v_{I}k}{\chi} \right) \right]$ (7.52)

Esli dlya faktora f prinyat' pervuyu formulu (7.51), to uslovie (7.52) ekvivalentno neravenstvu'

$v_{I} > \sqrt{\frac{2}{e}} \frac{\pi G \rho_{S}}{\chi (r)} = 0.85 \frac{\pi G \rho_{S}}{\chi (r)}$ (7.53)

Bolee tochnyi raschet, uchityvayushii tochnoe vyrazhenie funkcii f, daet chislennyi .mnozhitel', ravnyi 0,34. Takim obrazom, zvezdnyi disk mozhet sushestvovat' tol'ko v tom sluchae, esli dispersiya skorostei zvezd bol'she opredelennogo predela, kotoryi zdes' igraet rol' skorosti zvuka v neustoichivosti Dzhinsa. Esli kriterii (7.53) ne vypolnen, to vrashayushiisya zvezdnyi disk raspadaetsya na otdel'nye sgusheniya.

Esli podstavit' v_I iz (7.53) v opredelenie vremeni relaksacii odnorodnogo zvezdnogo diska ((7.34) pri $\overline{M} = M_{\Phi}$ ), to poluchim:

$t_{E} \gtrsim \frac{G^{3} \rho_{S}^{4}}{RM \Omega^{4}}$ (7.54)

gde takzhe prinyato χ ∼ Ω.

Odnako osnovnoe znachenie voln plotnosti v zvezdnom diske zaklyuchaetsya v tom, chto pri ih pomoshi mozhno ob'yasnit' spiral'nuyu strukturu galaktik - v etom zaklyuchaetsya osnovnaya ideya teorii spiral'noi struktury Lina - Shu (sm. [12-15]). Formula (7.50) opisyvaet volny plotnosti v vide koncentricheskih krugov, a dispersionnoe sootnoshenie

$[\omega - m \Omega (r)]^{2} = \chi^{2} - 2 \pi \rho_{S} |k| G f$ (7.55)

opisyvaet takzhe volny plotnosti, no imeyushie formu spiralei, zakruchivayushihsya pri k < 0 i raskruchivayushihsya pri k > 0. Zdes' m - celoe chislo, opredelyayushee kolichestvo cpiral'nyh rukavov.

Vsya spiral'naya struktura vrashaetsya s uglovoi skorost'yu

$\Omega_{p} = \frac{\omega}{m}$ (7.56)

gde ω opredelyaetsya uravneniem (7.55). Obychno v galaktikah imeetsya dva spiral'nyh rukava, t. e. m=2. Rasstoyanie mezhdu sosednimi vitkami spirali ravno λ / m. Spiral'naya struktura zanimaet ie ves' vrashayushiisya disk, a tol'ko polosu, v kotoroi vypolneno uslovie

$\Omega (r) - \frac{\chi (r)}{m} < \Omega_{p} < \Omega (r) + \frac{\chi (r)}{m}$ (7.57)

Chem bol'she chislo rukavov, tem uzhe zanimaemaya imya oblast'.

Spiral'nye volny plotnosti ne tol'ko vrashayutsya s opredelennoi uglovoi skorost'yu, no takzhe i peremeshayutsya vdol' radiusa s gruppovoi skorost'yu [16]

$v_{g} = \frac{d \omega}{dk} \approx - \frac{\pi G \rho_{S}}{\Omega_{p}/m}$ (7.58)

Eto privodit k tomu, chto spiral'nye volny plotnosti vse vremya styagivayutsya k centru galaktiki i trebuetsya ih postoyannaya "podkachka" dlya sohraneniya vsei spiral'noi kartiny v techenie dostatochno dolgogo promezhutka vremeni.

Sopostavlenie nablyudenii i teorii (sm. [13, 14]) daet v obshem soglasovannuyu kartinu, ob'yasnyayushuyu real'nuyu strukturu nashei Galaktiki i neskol'kih sosednih galaktik. Mnogo problem teorii spiral'noi struktury ostaetsya nereshennymi, iz nih naibolee trudnaya - problema vozbuzhdeniya spiral'nyh voln plotnosti. V svyazi s etim bol'shoe vnimanie udelyalos' chislennomu modelirovaniyu zvezdnyh sistem. Etomu voprosu budet posvyashen razdel 5.

<< § 7.2 Vremya relaksacii zvezdnyh sistem | Oglavlenie | § 7.4 Chislennoe modelirovanie evolyucii zvezdnyh skoplenii >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

$f \left( \frac{v_{I}k}{\chi} \right) = \exp \left( - \frac{v_{I}^{2}k^{2}}{\chi^{2}} \right) \quad (v_{I}k \ll \chi)$	(7.51)
$f \left( \frac{v_{I}k}{\chi} \right) = \left( \frac{2}{\pi} \right)^{1/2} \left( \frac{\chi^{2}}{v_{I}^{2}k^{2}} \right)^{3/2} \quad (v_{I}k \gg \chi)$