Astronet > Razmernosti i podobie astrofizicheskih velichin

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 7.3 Volny plotnosti vo vrashayushihsya galaktikah | Oglavlenie | § 7.5 Chislennoe modelirovanie ploskih vrashayushihsya galaktik >>

§ 7.4 Chislennoe modelirovanie evolyucii zvezdnyh skoplenii

Razvitie vychislitel'noi tehniki dalo vozmozhnost' postavit' zadachu o neposredstvennom chislennom eksperimente s model'yu zvezdnoi sistemy, sostoyashei iz bol'shogo chisla material'nyh tochek, vzaimodeistvuyushih mezhdu soboi po zakonu N'yutona. Reshenie etoi zadachi v principe zaklyuchaetsya v pryamom chislennom reshenii sistemy (7.1) pri nekotoryh zadannyh granichnyh usloviyah. Takim putem mozhno prosledit' evolyuciyu zvezdnoi sistemy, poluchit' takuyu ee harakteristiku, kak raspredelenie koncentracii zvezd vnutri sistemy, opredelit' chislo vyletevshih zvezd. Nakonec, v principe mozhno bylo by izuchit' povedenie zvezdnoi sistemy v zavisimosti ot vybora nachal'nyh uslovii.

K sozhaleniyu, prakticheskoe vypolnenie etoi programmy natalkivaetsya na mnogo trudnostei. Prezhde vsego sleduet otmetit', chto ob'em vychislenii ochen' bystro rastet s uvelicheniem chisla zvezd N, primerno kak N⁴. Pravda, est' special'nye metody, uproshayushie schet, no privodyashie k potere tochnosti i obshnosti.

Poetomu pervye raboty rassmatrivali skopleniya iz nebol'shogo chisla zvezd. V rabotah Hornera [17] rassmatrivalis' zvezdnye skopleniya, sostoyashie iz 16 i 25 zvezd (sm. takzhe [18]). Putem chislennogo resheniya sistemy (7.1) opredelyalos' raspredelenie koncentracii zvezd v zavisimosti ot rasstoyaniya r do centra skopleniya, ustanovivsheesya cherez neskol'ko vremen relaksacii. V etih rabotah effekt vyleta zvezd iz skoplenii special'no ne izuchalsya. V rabotah [17, 18] na osnovanii chislennyh eksperimentov, a takzhe analiticheskih ocenok, bylo polucheno, chto po istechenii neskol'kih vremen relaksacii v zvezdnom skoplenii obrazuetsya bolee plotnoe szhimayusheesya yadro s raspredeleniem koncentracii zvezd n ∼ r^-12/5 i otnositel'no protyazhennoe galo s raspredeleniem n ∼ r^-15/4. V etih raschetah takzhe poluchilos', chto primerno za 20 vremen relaksacii (pri N = 25) yadro stanovitsya ochen' plotnym - teoreticheski stremitsya k beskonechnosti kak n ∼ (t-t₀)^-4/3, a iz chislennogo eksperimenta poluchilos' n ∼ (t-t₀)^-1.5. gde t₀ - nekotoroe harakternoe vremya kollapsa yadra. Pri etom yadro teryaet zvezdy kak N_yad ∼ (t-t₀)^1/3. V chislennyh raschetah prinimalos', chto evolyuciya skopleniya zakanchivalas', kogda v yadre skopleniya ostavalos' tri zvezdy.

V rabote [18] Horner proslezhivaet evolyuciyu yadra skoplenii vplot' do momenta vremeni, kogda zvezdy nachinayut stalkivat'sya, t. e. togda, kogda nuzhno uchityvat' i konechnyi radius zvezdy. Stolknovenie zvezd v plotnyh yadrah galaktik privlekalos' dlya ob'yasneniya yavlenii kvazarov.

Vazhnym etapom v razvitii chislennogo modelirovaniya sistem byla programma, provedennaya po iniciative Lekara [19]. Sut' etoi programmy zaklyuchalas' v sleduyushem.

Rassmatrivaetsya zvezdnoe skoplenie iz 25 zvezd odinakovoi massy. Zadayutsya nachal'nye koordinaty zvezd v skoplenii (s 16 znachashimi ciframi). Nachal'nye skorosti ravny nulyu. Tem samym opredelyaetsya nachal'naya potencial'naya energiya skopleniya. Dalee po sisteme uravnenii (7.1) rasschityvaetsya dal'neishaya evolyuciya skopleniya. Smysl vsei programmy byl v tom, chtoby na razlichnyh EVM v raznyh institutah po svoim programmam rasschityvalas' by evolyuciya odnogo p togo zhe skopleniya s odnimi i temi zhe nachal'nymi usloviyami. Sravnenie poluchennyh rezul'tatov pozvolyaet sudit', naskol'ko odnoznachny vyvody, poluchennye iz chislennyh eksperimentov so zvezdnymi skopleniyami. V rabote [19] i provoditsya takoe sopostavlenie.

Chislenno reshalas' bezrazmernaya sistema (7.12) pri Π = 1, q_i = 1, N = 25. V bezrazmernyh edinicah nachal'naya potencial'naya energiya skopleniya U = -0.2. Eta velichina dolzhna ostavat'sya i polnoi energiei skopleniya E do teh por, poka vylety zvezd ee ne izmenyat. Harakternoe vremya peresecheniya

$P = G \mathcal{M}^{5/2} / (2U)^{3/2}$ (7.59)

v bezrazmernyh edinicah ravno 4. Vremya relaksacii (7.32) v bezrazmernyh edinicah ravno 2,5 (v [19] ispol'zovana drugaya formula dlya vremeni relaksacii, otlichayushayasya ot (7.32) zamenoi 12 v znamenatele na 2 π, tak chto tam prinyato vremya relaksacii ravnym 4,9).

V nachal'nom sostoyanii vse skoplenie imeet radius 2,75 v bezrazmernyh edinicah.

Po standartnoi programme Lekara bylo provedeno 11 nezavisimyh raschetov. Rezul'taty ih takovy. Vnachale imeet mesto kollaps skopleniya. Za vremya τ = 5,4 v bezrazmernyh edinicah (t. e. za 1,6 vremen peresecheniya) radius skopleniya umen'shaetsya do 1,25, t. e. srednyaya plotnost' rastet v 10,6 raza. Pri etom obrazuetsya central'noe plotnoe yadro. Plotnost' sfery, soderzhashei 10 blizhaishih k centru zvezd, uvelichivaetsya v 345 raz. Takoi nachal'nyi kollaps skopleniya poluchilsya bolee ili menee odinakovym vo vseh nezavisimyh raschetah. No posleduyushaya evolyuciya skopleniya okazalas' ochen' razlichnoi v raznyh raschetah.

Na ris. 27 pokazan hod virial'nogo koefficienta, t. e. otnosheniya udvoennoi kineticheskoi energii k potencial'noi energii skopleniya

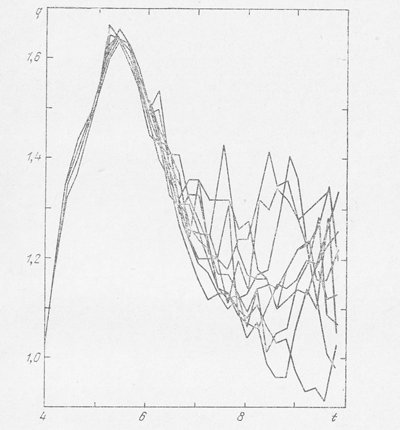
Ris. 27. Izmenenie so vremenem virial'nogo koefficienta (7.60) v standartnoi zadache 25 tel.

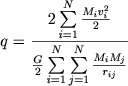
$q = \frac{2 \sum\limits_{i=1}^{N} \frac{M_{i}v_{i}^{2}}{2}}{\frac{G}{2} \sum\limits_{i=1}^{N} \sum\limits_{j=1}^{N} \frac{M_{i} M_{j}}{r_{ij}}}$ (7.60)

v zavisimosti ot vremeni. Srazu vidno, chto esli nachal'nyi kollaps protekaet odinakovo vo vseh raschetah, to posleduyushee rasshirenie (umen'shenie q), a zatem i pul'sacii zvezdnogo skopleniya razlichayutsya v raznyh raschetah bolee chem vdvoe. Zametim, chto v kvaziravnovesnom sostoyanii virial'nyi koefficient dolzhen byt' blizok k edinice.

Srednie znacheniya dispersii radial'nyh i tangencial'nyh komponent skorosti v bezrazmernyh edinicah dany na ris. 28. Zdes' takzhe imeetsya bol'shoi razbros znachenii. Sleduet eshe 'Otmetit', chto mgnovennye znacheniya dispersii skorostei zametno fluktuiruyut s techeniem vremeni, no srednie po vremeni dispersii bolee ili menee postoyanny.

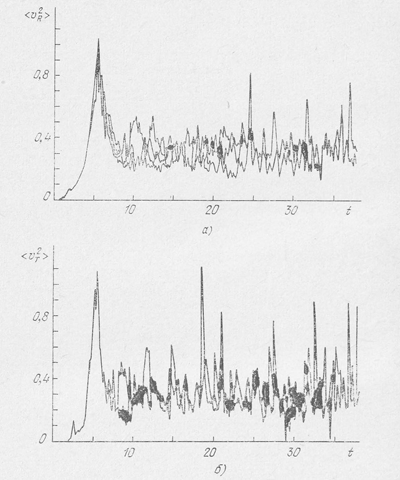
Ris. 28.

Osoboe vnimanie v rabote Lekara udelyalos' analizu processa vyleta zvezd iz skopleniya. K sozhaleniyu, i zdes' raznye raschety davali razlichnoe chislo vyletevshih zvezd - ot 1 do 5. Esli usrednit' rezul'taty vseh raschetov, to za vremya, ravnoe dvum harakternym vremenam relaksacii, otschityvaemym ot nachala rascheta, skoplenie poteryalo tri zvezdy ili 6% ot polnogo chisla zvezd za odno vremya relaksacii. Eta velichina na poryadok bol'she, chem sleduet iz teorii (0,74%). Nado takzhe otmetit', chto v raznyh raschetah vyletali raznye zvezdy i ne bylo ni odnogo sluchaya, chtoby odna konkretnaya zvezda vyletela by v kazhdom raschete. Chashe vsego vyletala konkretnaya zvezda za nomerom 25 (v vos'mi raschetah iz 11), zvezdy za nomerami 18 i 6 vyleteli v shespi raschetah iz 11. Est' zvezdy, kotorye vyleteli tol'ko v odnom iz 11 raschetov.

Ob'yasnenie vseh etih rashozhdenii, po krainei mere otchasti, mozhet byt' svyazano s vyborom nachal'nyh uslovii, privodyashih k bystromu kollapsu skopleniya. V samom dele, srazu zhe posle nachala scheta iz-za nulevyh nachal'nyh skorostei skoplenie bystro szhimaetsya i skorosti zvezd stol' zhe bystro uvelichivayutsya. Eto i otrazhaetsya na rezkom uvelichenii virial'nogo koefficienta. Bystroe uvelichenie skorostei zvezd delaet bolee veroyatnym vylet zvezd iz skoplenii. Krome togo, uplotnenie skopleniya yaa nachal'nom etape uvelichivaet obmen energiei mezhdu zvezdami, chto takzhe povyshaet veroyatnost' vyleta zvezd. Nakonec, rezkoe izmenenie sostoyaniya skopleniya na nachal'nom etape, po-vidimomu, uvelichivaet i oshibki scheta. Dlya polucheniya bolee soglasovannyh rezul'tatov sledovalo by povtorit' podobnuyu programmu odnovremennogo rascheta, no s drugim vyborom nachal'nogo sostoyaniya tak, chtoby izbezhat' etogo kollapsa.

Ochen' ser'eznoi trudnost'yu chislennogo eksperimenta v probleme N gravitiruyushih tel yavlyaetsya to, chto v uravneniyah sistemy (7.1) imeyutsya osobye tochki r_ij → 0. Pri sblizheniyah lyuboi pary zvezd sootvetstvuyushii chlen v uravneniyah (7.1) bystro rastet. Eto v svoyu ochered' bystro uvelichivaet oshibki scheta. Dlya sohraneniya tochnosti prihoditsya umen'shat' shag scheta kak po koordinate, tak i po vremeni. Eto zamedlyaet chislennoe integrirovanie i privodit k bol'shei neodnoznachnosti. Ukazannyi effekt takzhe ob'yasnyaet rashodimost' rezul'tatov scheta v standartnoi probleme 25 tel.

Vyhodom iz etogo zatrudneniya mozhet byt' modifikaciya potenciala gravitacionnogo vzaimodeistviya na malyh rasstoyaniyah. V chastnosti, v rabote V. I. Aleshina i S. A. Kaplayaa [20] vmesto obychnogo vyrazheniya dlya potencial'noi energii zvezd vida GM_iM_j / r_ij bylo prinyato vyrazhenie

$V_{ij} = - \frac{GM_{i}M_{j}}{r_{ij}} \left( 1 - \frac{\epsilon}{r_{ij}^{2}} \right)$ (7.61)

gde ε - nekotoraya postoyannaya, vybrannaya iz soobrazhenii udobstva scheta. Nekotorye fizicheskie soobrazheniya v pol'zu takogo vybora obsuzhdayutsya v rabote [20]. Zdes' zhe zametim, chto ispol'zovanie potenciala (7.61) umen'shaet veroyatnost' tesnyh sblizhenii, a sledovatel'no, i nachal'noe szhatie.

V rabote [20] bylo provedeno chislennoe .modelirovanie evolyucii skopleniya iz 25 tel pri teh zhe nachal'nyh usloviyah, chto i v standartnoi programme Lekara. Blagodarya otsutstviyu tesnyh sblizhenii raschet evolyucii skopleniya mozhno provesti gorazdo dal'she po vremeni. Esli v obychnoi programme Lekara naibolee dlinnyi raschet zanimal 10 vremen peresechenii, to v raschete [20] byla proslezhena evolyuciya skopleniya za 30 vremen peresechenii. Rezul'taty rascheta [20] v obshem soglasuyutsya s raschetami [19]. Eto pokazyvaet, chto zamena deistvitel'nogo potenciala gravitacionnogo vzaimodeistviya na vyrazhenie (7.61) ne privodit k kardinal'nym izmeneniyam. Na ris. 29 priveden hod virialshogo koefficienta. Sushestvennyh otlichii ot ris. 27 net.

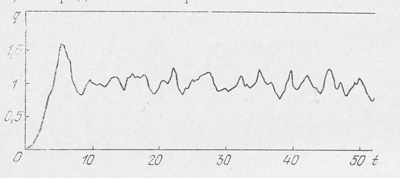
Ris. 29. Virial'nyi koefficient v zadache 25 tel s potencialom vzaimodestviya, imeyushim vid (7.61)

Na ris. 30 privedeny dispersiya radial'nyh i tangencial'nyh komponent skorostei zvezd. V principe etot risunok malo otlichaetsya ot ris. 28. Zdes' takzhe tangencial'nye skorosti pokazyvayut bol'shie fluktuacii, chem radial'nye skorosti.

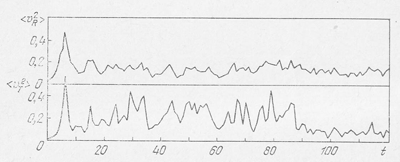
Ris. 30. Dispersiya radial'nyh (vverhu) i tangencial'nyh (vnizu) skorostei zvezd v zadache 25 tel s potencialom vzaimodestviya, imeyushim vid (7.61)

V raschete [20] na stadii, neposredstvenno sleduyushei za pervonachal'nym kollapsom, vyletalo dve zvezdy, v tom chisle za nomerom 25, t. e. ta zvezda, kotoraya chashe vsego vyletala i v raschetah [19]. Vse eto proishodilo za pervye dva vremeni relaksacii. V techenie posleduyushih primerno 20 vremen relaksaciei vyletalo tri zvezdy. Sledovatel'no, za odno vremya relaksacii kvazistacionarnogo sostoyaniya vyletaegt 0,6% ot polnogo chisla zvezd. Eto uzhe blizhe k teoreticheskim ocenkam. Poluchivsheesya dazhe bolee nizkoe, chem v teorii, znachenie legko ob'yasnit' tem, chto vvedenie parametra k v (7.61) zametno umen'shaet veroyatnost' sblizhenii, a sledovatel'no, i vozmozhnost' priobreteniya bol'shih skorostei zvezdami skopleniya.

Teper' rassmotrim raboty, posvyashennye chislennomu modelirovaniyu zvezdnyh skoplenii s bol'shim chislom zvezd (N ≈100-250).

Aarset [21] issledoval evolyuciyu skopleniya iz 250 zvezd metodom chislennogo eksperimenta, ispol'zuya vyrazhenie dlya potencial'noi energii gravitacionnogo vzaimodeistviya dvuh zvezd v vide

$V_{ij} = - \frac{GM_{i}M_{j}}{(r_{ij}^{2}+\epsilon)^{1/2}}$ (7.62)

gde ε - takzhe nekotoraya postoyannaya velichina. Drugoe otlichie etoi raboty ot opisannyh vyshe v tom, chto zdes' predpolagalos' razlichie mass zvezd. Ispol'zovana sleduyushaya funkciya raspredeleniya zvezd po massam (tabl. 12):

Tablica 12

Raschet evolyucii takogo skopleniya byl proslezhen v techenie 28 vremen peresecheniya. Sushestvennoi osobennost'yu evolyucii etogo skopleniya yavlyaetsya obrazovanie dvoinyh sistem, naprimer, dve samye tyazhelye zvezdy s massami 25 edinic bystro obrazuyut dvoinuyu sistemu v centre skopleniya. Sushestvovanie etoi pary sil'no menyaet ves' harakter evolyucii, v chastnosti, privodit k bolee bystromu vyletu zvezd iz skopleniya.

V rezul'tate evolyucii v skoplenii ustanavlivaetsya nekotoroe kvaziravnovesnoe raspredelenie koncentracii zvezd v zavisimosti ot rasstoyaniya do centra skopleniya. Otnositel'noe umen'shenie zvezd v central'noi oblasti- skopleniya ob'yasnyaetsya bol'shoi rol'yu vyleta zvezd iz etoi oblasti, takzhe obyazannoi vliyaniyu central'noi massivnoi pary. V srednem po skopleniyu n ∼ r^-3, vo vneshnei chasti (galo) luchshe podhodit zavisimost' n ∼ r^-4, chto v obshem horosho soglasuetsya s rezul'tatami [18]

V rabote [21] podrobno izuchalas' ya osnovnaya zadacha chislennogo eksperimenta so skopleniyami - opredelenie chisla vyletevshih zvezd za odno vremya relaksacii. Rezul'taty chislennogo eksperimenta [21] pokazali, chto v srednem za odno vremya relaksacii vyletaet 3,4% polnogo chisla zvezd. Opredelena takzhe zavisimost' zvezd ot ih massy. V chastnosti, za odno vremya relaksacii vyletaet 2,5% ot chisla zvezd samyh malyh mass. Interesno, chto esli za pervuyu polovinu proschitannogo vremeni evolyucii vyletelo 44 zvezdy, to za vtoruyu polovinu etogo vremeni vyletelo vsego 24 zvezdy. Nachal'naya bystraya poterya zvezd mozhet byt' ob'yasnena szhatiem skopleniya, zatem znachitel'noe chislo zvezd vyletaet v to vremya, kogda obrazovavshayasya v centre skopleniya para zvezd s massami v 25 edinic eshe imeet bol'shoe rasstoyanie mezhdu komponentami. Otdavaya energiyu drugim zvezdam skopleniya, eta para stanovitsya bolee tesnoi, a te zvezdy, s kotorymi eta para vzaimodeistvuet, poluchiv bol'shuyu energiyu, vyletayut iz skopleniya. Posle togo kak central'naya tyazhelaya para stanovitsya dostatochno tesnoi, ee vzaimodeistvie s ostal'nymi zvezdami stanovitsya menee effektivnym i vylet zvezd zamedlyaetsya. Ekstrapolyaciya raschetov pokazyvaet, chto skoplenie dolzhno poteryat' polovinu zvezd primerno za 60 periodov peresecheniya.

Kak uzhe otmechalos', v dannom chislennom eksperimente poluchilas' slishkom bol'shaya skorost' vyleta zvezd po sravneniyu s teoreticheskim raschetom (3,4% vmesto 0,74%). Analiz chislennogo scheta pokazyvaet, chto iz 68 vyletevshih zvezd 45 priobreli parabolicheskuyu skorost' neposredstvenno vblizi central'noi pary, eshe 16 zvezd uskorilis' v raione central'nogo yadra (pri g < 1).. Eto oznachaet, chto process vyleta zvezd v dannom sluchae opredelyaetsya glavnym obrazom tyazheloi central'noi paroi i poetomu poluchennoe vysokoe znachenie dlya skorosti vyleta netipichno dlya skopleniya bez takih central'nyh par.

Problema vyleta zvezd iz skopleniya na osnove metoda chislennogo integrirovaniya rassmatrivalas' takzhe Vilenom [22]. Izuchalas' evolyuciya skopleniya iz 100 zvezd, no rassmatrivalis' raznye modeli. Vo vseh modelyah, krome odnoi, uchityvalas' neodinakovost' mass so sleduyushei funkciei raspredeleniya (tabl. 13)

Tablica 13

Predpolagalis' razlichnye nachal'nye usloviya, uchityvalos' vrashenie skopleniya i vliyanie vneshnego gravitacionnogo polya galaktiki. V etoi rabote reshalas' sistema uravnenii (7.1) v ee chistom vide (t. e. s potencialom, imeyushim osobennosti pri r_ij → 0), i poetomu evolyuciya kazhdoi modeli byla proslezhena vsego na 5-12 vremen peresecheniya. Chtoby poluchit' bolee uverennye statisticheskie dannye o vylete zvezd, v rabote summirovalos' vremya evolyucii modelei. Naprimer, v treh modelyah s raznymi massami zvezd za summarnoe vremya evolyucii, ravnoe 30 vremenam peresecheniya, vyletelo 23 zvezdy. Eto znachenie bolee ili menee sootvetstvuet teoreticheskim ocenkam [3, 6, 7]. Odnako raschet modeli s ravnymi massami pri prochih odinakovyh usloviyah, proslezhennyi na 9,6 vremen peresecheniya, ne privel k vyletu hotya by odnoi zvezdy. Ekstrapoliruya dannye o modeli s raznymi massami i uchityvaya teoreticheskie ocenki, mozhno bylo by ozhidat', chto za eto vremya vyletit sem' zvezd. Veroyatnost' togo, chto sluchaino ne vyletelo ni odnoi zvezdy, ochen' mala, vsego okolo 6 × 10^-4

Drugoe rashozhdenie s teoriei svyazano s raspredeleniem vyletevshih zvezd po massam. Teoreticheski zvezdy malyh mass vyletayut zametno chashe, chem zvezdy srednih mass, a v chislennom eksperimente [22] poluchilos', chto raspredelenie vyletevshih zvezd po massam primerno sootvetstvuet ih raspredeleniyu v samom skoplenii. Naprimer, zvezd s massoi 0,55 v modeli skopleniya v 2,6 raza bol'she, chem zvezd so srednei massoi 1,1; vyletelo zvezd s maloi massoi v 2,5 raza bol'she, chem zvezd so srednei massoi, a teoreticheski skoplenie dolzhno poteryat' zvezd s massoi 0,55 primerno v 15 raz bol'she, chem zvezd s massoi 1,1.

V rabote [22] obsuzhdayutsya prichiny takih rashozhdenii s teoriei, no nado otmetit', chto i teoreticheskie ocenki chisla i raspredeleniya mass vyletevshih zvezd takzhe neodnoznachny. Avtor raboty [22] schitaet, chto ego rezul'taty luchshe soglasuyutsya s rabotoi [8]. V rabote [22] rassmatrivalsya takzhe sluchai, kogda v processe evolyucii dve samye massivnye zvezdy (s massami 4,4) vnezapno teryali svoyu massu i prevrashalis' v malye zvezdy s massami 0,55. Eto privodilo k zametnomu uskoreniyu vyleta zvezd.

Privedem kolichestvennye rezul'taty. Rassmatrivalos' skoplenie, kotoroe za pervye 10 vremen peresechenii, poka massy zvezd 4,4 ostavalis' neizmennymi, poteryalo shest' zvezd. Zatem srazu zhe posle vnezapnogo umen'sheniya massy dvuh tyazhelyh zvezd eto skoplenie prakticheski mgnovenno poteryalo eshe tri zvezdy, a za posleduyushie pyat' vremen peresechenii ono poteryalo eshe sem' zvezd.

Rezul'taty chislennogo eksperimenta Videna [22] naglyadno pokazyvayut, chto eshe mnogo predstoit vyyasnit' s cel'yu soglasovaniya teorii i chislennogo eksperimenta.

Kak uzhe otmechalos', osnovnoi prichinoi oshibok scheta i glavnoi trudnost'yu v postroenii chislennyh modelei zvezdnyh skoplenii 'yavlyayutsya osobye tochki v uravneniyah sistemy (7.1), poyavlyayushiesya pri r_ij → 0, t. e. pri tesnyh sblizheniyah zvezd. Dlya preodoleniya etoi trudnosti v chislennyh raschetah eshe v 1903 g. Levi-Chivita predlozhil metod regulyarizacii. Etot metod byl obobshen Kustanheimo i Shtifelem [23], a primenitel'no k zvezdnym skopleniyam metod obsuzhdalsya v [24 - 26]. Metod regulyarizacii udobnee poyasnit' na primere odnomernogo dvizheniya (lobovogo stolknoveniya dvuh material'nyh tochek). Zdes' uravnenie dvizheniya:

$\frac{d^{2}x}{dt^{2}} = - \frac{GM}{x^{2}}$ (7.63)

gde h - rasstoyanie mezhdu tochkami i M - privedennaya massa. Iz (7.63) sleduet integral energii

$\frac{1}{2} \left( \frac{dx}{dt} \right)^{2} - \frac{GM}{x} = -W$ (7.64)

gde W - polnaya enerpiya, otnesennaya k edinice massy. Pri chislennom reshenii (7.63) s zadannoi tochnost'yu prihoditsya vse vremya umen'shat' shag po vremeni po mere umen'sheniya x, i pri x → 0 shag po vremeni stanovitsya beskonechno malym. Dlya togo chtoby izbezhat' etogo, v metode Levi-Chivita vvoditsya reducirovannoe vremya τ,

$d \tau = \frac{dt}{x}$ (7.65)

s tem, chtoby odnovremennoe umen'shenie shaga po t i x ostavlyalo shag po τ konechnym. S zamenoi (7.65) uravneniya (7.63) i (7.64) priobretut vid

$\frac{d^{2}x}{d \tau^{2}} = GM -2xW$ (7.66)

$\frac{1}{2} \left( \frac{dx}{d \tau} \right)^{2} - GMx + Wx^{2} = 0$ (7.67)

Zdes' uzhe net osobennosti v nulevoi tochke, i chislennoe integrirovanie (7.66) provoditsya bez zatrudnenii. Sobstvenno, netrudno poluchit' i analiticheskoe reshenie (7.66), no nasha cel' - pokazat', kak ustranyaetsya osobennost'.

Obobshenie Kustanheimo i Shtifelya na trehmernyi sluchai zaklyuchaetsya vo vvedenii ne tol'ko reducirovannogo vremeni

$d \tau = \frac{dt}{r}$ (7.68)

no i reducirovannyh koordinat u₁, u₂, u₃ i u₄.

$x = u_{1}^{2} - u_{2}^{2} - u_{3}^{2} + u_{4}^{2}$

$y = 2(u_{1}u_{2} - u_{3}u_{4})$

$z = 2(u_{1}u_{3} + u_{2}u_{4})$

$r^{2} = u_{1}^{2} + u_{2}^{2} + u_{3}^{2} + u_{4}^{2}$ (7.69)

V peremennyh (7.68) - (7.69) sistema uravnenii dlya trehmernogo dvizheniya dvuh tel imeet vid

$\frac{d^{2}u_{i}}{d \tau^{2}} = - \frac{1}{2} W u_{i} \quad i=\overline{1,4}$ (7.70)

gde W - po-prezhnemu velichina polnoi energii otnositel'nogo dvizheniya, rasschitannaya na edinicu massy. V staryh i novyh peremennyh

$W = \frac{1}{2} \left( \frac{dr}{dt} \right)^{2} - \frac{GM}{r} = \frac{1}{r} \left[ 2 \sum\limits_{i=1}^{4} \left( \frac{du_{i}}{d \tau} \right)^{2} -GM \right]$ (7.71)

Sistema (7.70) takzhe ne imeet osobennostei v nulevoi tochke i ne predstavlyaet trudnostei dlya chislennogo integrirovaniya.

Nakonec, obobshenie metoda regulyarizacii na sluchai zadachi mnogih tel svoditsya k vvedeniyu reducirovannogo vremeni po formule

$d \tau = \sum\limits_{i=1}^{N} \sum\limits_{i=1}^{N} \frac{M_{i}M_{j}}{r_{ij}} dt$ (7.72)

gde, po-prezhnemu, r_ij - rasstoyanie mezhdu zvezdami M_i, M_j. Reducirovannye koordinaty vvodyatsya analogichno (7.69)

Zdes' takzhe ischezayut osobennosti v nulevyh tochkah, no sistema uravnenii dvizheniya zvezd v skopleniyah stanovitsya ochen' gromozdkoi. Vozmozhno imenno poetomu opisannyi metod regulyarizacii eshe ne nashel shirokogo primeneniya v chislennyh eksperimentah so zvezdnymi skopleniyami. Chashe vse zhe upotreblyayutsya prostye vidoizmeneniya potenciala gravitacionnogo vzaimodeistviya (7.61) ili (7.62).

Drugoi uproshennyi metod chislennogo eksperimenta so zvezdnymi skopleniyami predlozhili T. A. Agekyan i A. S. Baranov [27, 28]. V etom metode uravneniya sistemy (7.1) reshayutsya dlya nebol'shogo chisla zvezd, naprimer, dlya N = 5. Zatem srednyaya koncentraciya zvezd v skoplenii v nekotorom ob'eme na zadannom rasstoyanii ot centra opredelyaetsya dlya vremeni, provodimogo vsemi zvezdami v etom ob'eme. Kazhdaya iz N zvezd pobyvaet v kazhdom dannom ob'eme mnogo raz i esli vremya scheta dostatochno veliko, to opredelennaya podobnym obrazom srednyaya koncentraciya statisticheski dostoverna. Takim zhe obrazom mozhno opredelit' i srednie skorosti i dispersii skorostei. Razumeetsya, etot metod ne pozvolyaet izuchat' vylet zvezd iz skopleniya, hotya i zdes' dlya ocenok mozhno opredelit' dolyu vremeni, provodimogo zvezdami na dalekih rasstoyaniyah ot skopleniya. Etim metodom v rabotah [27, 28] .issledovany struktura i raspredelenie skorostei v kvazistacionarnyh skopleniyah zvezd s odinakovymi i raznymi massami. Pri reshenii sistemy (7.1) prinyato N = 5.

V zaklyuchenie etogo paragrafa otmetim, chto v rabotah [29, 30] rassmatrivalsya chislennyi eksperiment so skopleniyami gravitiruyushih po zakonu N'yutona tel, no s uchetom izmeneniya ih mass. V rabote [29] predpolagalos', chto sistema tel pogruzhena v plotnoe tazo-pylevoe oblako i chto imeet mesto akkreciya veshestva na eti tela. Opredelyalis' funkcii raspredeleniya mass. Rezul'taty chislennogo eksperimenta pokazali, chto medlennye zvezdy skopleniya bystree nabirayut massu, chto v svoyu ochered' privodit k eshe bol'shemu ih zamedleniyu i k eshe bolee bystromu rostu massy. Eto oznachaet, chto v podobnyh skopleniyah zvezd s akkreciei bolee veroyatno obrazovanie nebol'shogo chisla zvezd s bol'shei massoi, chem ravnoraspredelenie massy po bol'shemu chislu zvezd.

V rabote [30] metodom chislennogo eksperimenta rassmotreno skoplenie bol'shogo chisla tel, dvizhushihsya pod deistviem vzaimnogo gravitacionnogo prityazheniya i okazavshihsya vblizi drug ot druga. Takoi raschet mozhet modelirovat' obrazovanie planet i ih sputnikov iz protoplanetnoi sredy. Zdes' takzhe okazalos', chto proishodit preimushestvennoe obrazovanie odnogo ili neskol'kih tel bol'shoi massy, u kotoryh mogut okazat'sya zahvachennymi sputniki -tela, ostavshiesya s maloi massoi.

<< § 7.3 Volny plotnosti vo vrashayushihsya galaktikah | Oglavlenie | § 7.5 Chislennoe modelirovanie ploskih vrashayushihsya galaktik >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce