Astronet > Razmernosti i podobie astrofizicheskih velichin

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 7.4 Chislennoe modelirovanie evolyucii zvezdnyh skoplenii | Oglavlenie | § 8.1 Struktura kvazarov i yader galaktik >>

§ 7.5 Chislennoe modelirovanie ploskih vrashayushihsya galaktik

Dlya chislennogo modelirovaniya sistem, sostoyashih iz 10¹⁰ - 10¹² zvezd, neobhodimo reshat' sistemy tipa (7.1) dlya ochen' bol'shogo chisla tel, kak, naprimer, N ≈ 10⁴ - 10⁵. Razumeetsya, pryamoe chislennoe integrirovanie (7.1) s pomosh'yu sovremennyh EVM dlya etogo sluchaya poka nevozmozhno. Poetomu ispol'zuetsya drugoi metod, kotoryi my seichas i opishem.

Vyrazim uskorenie i-i zvezdy cherez velichinu potenciala vsei zvezdnoi sistemy v tochke nahozhdeniya etoi zvezdy

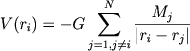
$V(r_{i}) = - G \sum\limits_{j=1, j \ne i}^{N} \frac{M_{j}}{|r_{i}-r_{j}|}$ (7.73)

Uravneniya dvizheniya budut imet' vid

$\frac{d^{2}r_{i}}{dt^{2}} = - \mbox{grad} V(r_{i})$ (7.74)

Posledovatel'nost' vychislenii v etom metode zaklyuchaetsya v sleduyushem. Razob'em prostranstvo na setku yacheek i zadadimsya nekotorym raspredeleniem zvezd v etom prostranstve. Po etomu raspredeleniyu vychislim znacheniya potencialov v kazhdoi yacheike (naprimer, v centrah). Zatem, v sootvetstvii s uravneniem (7.74), vychislim uskorenie dannoi zvezdy, chto pozvolit opredelit' skorost' i novoe polozhenie kazhdoi zvezdy cherez odin shag po vremeni. Poluchaem novoe raspredelenie zvezd v prostranstve. Zatem snova vychislyaem potencial po novomu raspredeleniyu zvezd, opyat' nahodim uskorenie vseh zvezd i t. d. Trudnostei s uchetom zvezdnyh sblizhenii zdes' net blagodarya tomu, chto, vychislyaya Potencial v centrah kazhdoi yacheiki, my uchityvaem tol'ko vklad ot teh zvezd, kotorye raspolozheny v drugih yacheikah. Summirovanie pri vychislenii potenciala po 'bol'shomu chislu zvezd takzhe mozhet byt' uprosheno, esli otnesti polozhenie vseh zvezd, okazavshihsya v dannoi yacheike, k ee centru. Nakonec i raschet dvizheniya zvezd mozhet byt' uproshen tem, chto mozhno schitat' peremesheniya diskretnymi, proishodyashimi putem perehodov iz centra odnoi yacheiki v centr drugoi yacheiki. Poetomu takim metodom udaetsya pri zatrate otnositel'no nebol'shogo mashinnogo vremeni rasschitat' zvezdnye sistemy, sostoyashie iz soten tysyach zvezd.

Dlya vychisleniya potenciala mozhno ispol'zovat' preobrazovanie Fur'e - eto v neskol'ko raz uskoryaet schet, hotya i trebuet bol'shei mashinnoi pamyati. Poka etot metod primenyalsya dlya modelirovaniya ploskih (dvumernyh) zvezdnyh sistem, imitiruyushih spiral'nye galaktiki. Cel'yu takih chislennyh eksperimentov i bylo vyyasnenie voprosa o neustoichivosti ploskih vrashayushihsya zvezdnyh diskov, o vozmozhnom poyavlenii zdes' spiral'noi struktury.

V ploskoi zvezdnoi sisteme potencial vyrazhaetsya cherez poverhnostnuyu plotnost' zvezd ρ^(s)(x, y)

$V(x, y) = - G \int\int \frac{\rho^{(s)}(x^{\prime}, y^{\prime}) dx^{\prime} dy^{\prime}}{\sqrt{(x-x^{\prime})^{2}+(y-y^{\prime})^{2}}}$ (7.75)

Razbivaya ploskost' zvezdnogo diska na setku s kvadratnymi yacheikami (chislo yacheek oboznachim cherez N₁ × N₂) i schitaya, chto teper' ρ^(s)_ik oznachaet chislo zvezd edinichnoi massy v yacheike s nomerami i i k po osyam koordinat, imeem dlya potenciala v yacheike

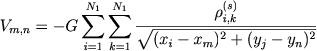
$V_{m, n} = - G \sum\limits_{i=1}^{N_{1}} \sum\limits_{k=1}^{N_{1}} \frac{\rho_{i,k}^{(s)}}{\sqrt{(x_{i}-x_{m})^{2}+(y_{j}-y_{n})^{2}}}$ (7.76)

gde x_m i y_n - koordinaty centrov yacheek. Komponenty uskoreniya v centrah yacheek:

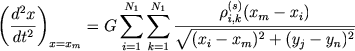
$\left( \frac{d^{2}x}{dt^{2}} \right)_{x=x_{m}} = G \sum\limits_{i=1}^{N_{1}} \sum\limits_{k=1}^{N_{1}} \frac{\rho_{i,k}^{(s)}(x_{m}-x_{i})}{\sqrt{(x_{i}-x_{m})^{2}+(y_{j}-y_{n})^{2}}}$

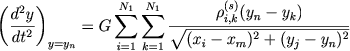
$\left( \frac{d^{2}y}{dt^{2}} \right)_{y=y_{n}} = G \sum\limits_{i=1}^{N_{1}} \sum\limits_{k=1}^{N_{1}} \frac{\rho_{i,k}^{(s)}(y_{n}-y_{k})}{\sqrt{(x_{i}-x_{m})^{2}+(y_{j}-y_{n})^{2}}}$ (7.77)

Mozhno opredelyat' uskorenie zvezd i po raznosti potencialov v sosednih yacheikah, ispol'zuya podhodyashie interpolyacionnye formuly.

Dlya sokrasheniya vremeni chislennogo scheta udobno vospol'zovat'sya preobrazovaniem Fur'e. Dlya etogo sleduet pereiti v (7.76) k celochislennym koordinatam, vybiraya za edinicu dliny storonu yacheiki. Togda zapishem (7.76) v bezrazmernom vide:

$V_{m, n} = - G \sum\limits_{i=1}^{N_{1}} \sum\limits_{k=1}^{N_{1}} H_{m-i, n-k} \rho_{i,k}^{(s)}$ (7.78)

gde ρ_{i, k}^(s) - polnaya massa zvezd v yacheike s koordinatami x_i = ia y_k = ka, a H_ij est' funkciya Grina dlya n'yutonovskogo potenciala:

$H_{ij}=\frac{1}{\sqrt{i^{2}+j^{2}}}$ (7.79)

Preobrazovanie Fur'e osvobozhdaet nas ot dvuhkratnogo summirovaniya v (7.78), zamenyaya etu formulu na prostoe sootnoshenie

$\tilde V_{m, n} = \tilde H_{m-i, n-k} \tilde \rho_{i,k}^{(s)}$ (7.80)

kuda vhodyat fur'e-obrazy sootvetstvuyushih velichin, a imenno

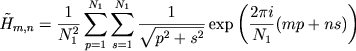
$\tilde H_{m, n} = \frac{1}{N_{1}^{2}} \sum\limits_{p=1}^{N_{1}} \sum\limits_{s=1}^{N_{1}} \frac{1}{\sqrt{p^{2}+s^{2}}} \exp \left(\frac{2 \pi i}{N_1{}} (mp+ns)\right)$ (7.81)

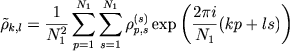
$\tilde \rho_{k, l} = \frac{1}{N_{1}^{2}} \sum\limits_{p=1}^{N_{1}} \sum\limits_{s=1}^{N_{1}} \rho_{p, s}^{(s)} \exp \left(\frac{2 \pi i}{N_1{}} (kp+ls)\right)$ (7.82)

i analogichno dlya $\tilde V_{m, n}$ . Fur'e-obraz funkcii Grina (7.81) hranitsya v pamyati EVM, a dlya vychisleniya $\tilde \rho_{k, l}^{(s)}$ i obratnogo preobrazovaniya Fur'e dlya opredeleniya V_{m, n} po $\tilde V_{m, n}$ , p, naidennogo iz (7.80), sushestvuyut standartnye programmy. Imenno po etoi metodike, hotya i razlichayusheisya v detalyah, provodilos' chislennoe modelirovanie ploskih vrashayushihsya galaktik.

Seriyu chislennyh eksperimentov po issledovaniyu ustoichivosti vrashayushegosya ploskogo diska proveli Hol' i Hoknei [31-34]. Modeli, prinyatye v etoi serii issledovanii, sostoyali iz 50000 ili 200000 zvezd, nahodyashihsya v ploskosti diska. Disk byl razdelen na setku iz 64 × 64 ili 128 × 128 yacheek (v raznyh variantah). V sootvetstvii s opisannym vyshe metodom opredelyalsya potencial v centrah yacheek pri pomoshi preobrazovaniya Fur'e i rasschityvalos' dvizhenie zvezd po dvoinym interpolyacionnym formulam, uchityvayushim znachenie potenciala v chetyreh sosednih yacheikah. Nahodilos' novoe raspredelenie plotnosti i vychislenie potenciala povtoryalos'. Shag po vremeni vybiralsya tak, chto disk zvezd sovershal polnyi oborot za 200 ili 400 shagov po vremeni. Okazalos', chto harakter evolyucii modeli slabo zavisit ot vybora chisla yacheek, chisla zvezd ili velichiny shaga po vremeni v ukazannyh vyshe predelah. Podrobno metod, primenennyi Holem i Hoknei, opisan v rabote [32]

Rezul'taty chislennogo eksperimenta mozhno summirovat' sleduyushim obrazom. V rabote [34] izuchalas' ustoichivost' zvezdnogo diska v zavisimosti ot vybora dispersii skorostei zvezd v predpolozhenii, chto vrashenie diska imeet tverdotel'nyi harakter, t. e. proishodit s postoyannoi uglovoi skorost'yu po krainei mere v nachal'nyi moment vremeni. Tverdotel'noe vrashenie imeet mesto, esli raspredelenie poverhnostnoi plotnosti zvezd opisyvaetsya formuloi:

$\rho^{(s)} (r) = \rho_{0}^{(s)} \sqrt{1-r^{2}/R^{2}}$ (7.83)

Uglovaya skorost' vrasheniya vyrazhaetsya cherez plotnost' v centre diska ρ₀^(s) formuloi

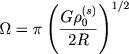
$\Omega = \pi \left( \frac{G\rho_{0}^{(s)}}{2R} \right)^{1/2}$ (7.84)

gde R - polnyi radius diska. Rassmatrivalos' neskol'ko variantov, otlichayushihsya drug ot druga raznym zadaniem nachal'noi dispersii skorostei zvezd, prichem schitalos', chto v nachal'nyi moment dispersiya skorostei zvezd v dannom meste sostavlyaet opredelennyi procent ot kvadrata lineinoi skorosti vrasheniya diska v tom zhe meste.

Na ris. 31 pokazana evolyuciya diska zvezd, poluchennaya v etih modelyah dlya sluchaya, kogda nachal'noi dispersii skorostei net voobshe. Vremya vyrazheno v periodah vrasheniya. Vidno, chto uzhe za odnu tret' oborota v diske obrazovalis' chetko vyrazhennye sgusheniya i k koncu odnogo oborota disk polnost'yu raspalsya, v polnom soglasii s rezul'tatami Tumre (sm. § 2 etoi glavy i [11]), t. e. vrashayushiisya ploskii disk galaktiki neustoichiv dlya vozmushenii s maloi dlinoi volny. Zatem na ris. 32-35 pokazana evolyuciya vrashayushegosya diska pri dispersii skorostei 6,8; 13,6; 20,4 i 27,2 % sootvetstvenno ot krugovoi skorosti. Vidno, kak s uvelicheniem dispersii skorostei disk stanovitsya vse menee podverzhennym raspadu na sgusheniya i v poslednem sluchae okazalsya ustoichivym, takzhe v polnom soglasii s teoreticheskimi vyvodami, t. e. s sootnosheniem (7.52) ili (7.53).

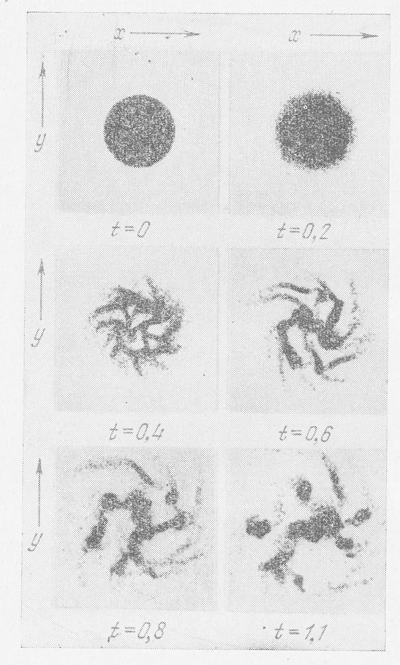
Ris. 31. Evolyuciya vrashayushegosya diska zvezd, v kotorom nachal'naya dispersiya skorostei zvezd ravna nulyu..

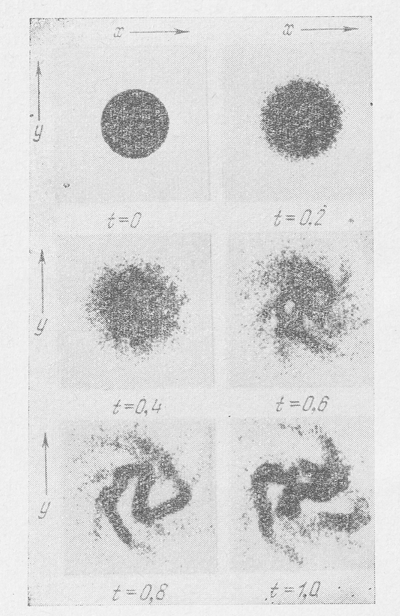
Ris. 32. To zhe, chto i na Ris. 31, no s nachal'noi dispersiei skorostei, ravnoi 6.8 % ot krugovoi skorosti na krayu diska...

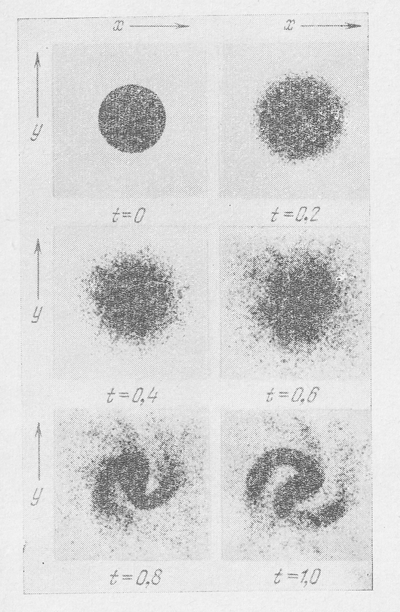
Ris. 33. To zhe, chto i na Ris. 31, no s nachal'noi dispersiei skorostei, ravnoi 13.6 % ot krugovoi skorosti na krayu diska...

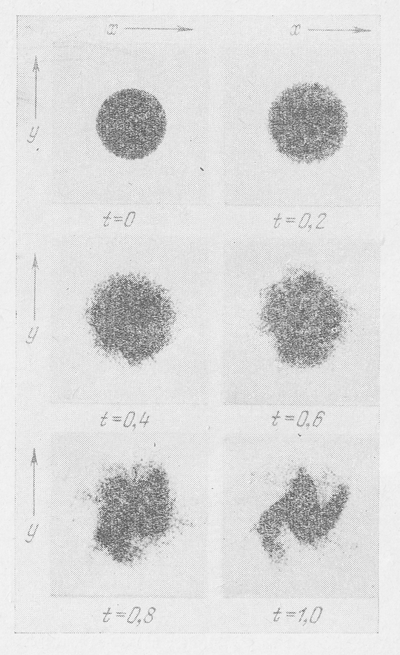
Ris. 34. To zhe, chto i na Ris. 31, no s nachal'noi dispersiei skorostei, ravnoi 20.4 % ot krugovoi skorosti na krayu diska...

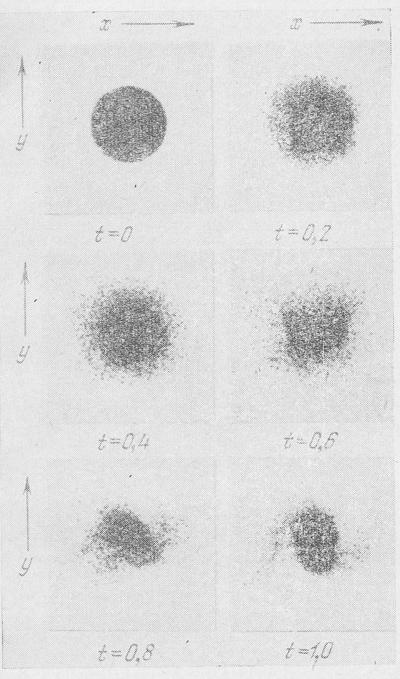
Ris. 35. To zhe, chto i na Ris. 31, no s nachal'noi dispersiei skorostei, ravnoi 27.2 % ot krugovoi skorosti na krayu diska. V etom sluchae kriterii neustoichivosti Tumre udovletvoryaetsya...

V rabote [32] rassmatrivalis' podobnye zhe modeli, no bylo prinyato drugoe raspredelenie poverhnostnoi plotnosti. Izuchalos' gaussovo ρ^(s) ∼ exp (-const r²) i eksponencial'noe ρ^(s) ∼ exp (-const r) raspredeleniya poverhnostnoi plotnosti. Kartina v obshem analogichna. Bez dispersii skorostei zvezd ili pri maloi dispersii disk okazyvaetsya neustoichivym, a vvedenie dostatochno bol'shoi dispersii skorostei sta'biliziruet disk.

Pravil'nye spiral'nye rukava poluchalis' v etih modelyah tol'ko dlya sluchaya, kogda v sisteme imelos' zametnoe central'noe uplotnenie, v kotorom sosredotochena bol'shaya chast' massy galaktiki. Odno i to zhe zvezdnoe uplotnenie mozhno bylo prosledit' v techenie vos'mi oborotov.

V rabote [32] izuchalas' takzhe puchkovaya neustoichivost' gravitacionnyh sistem. Dopustim, chto dva potoka zvezd s odinakovoi zvezdnoi plotnost'yu i odinakovoi dispersiei skorostei v_I, pronikayut drug cherez druga, dvigayas' s otnositel'noi skorost'yu v_R. Togda, kak izvestno iz teorii, oba potoka dolzhny raspast'sya na otdel'nye sgusheniya i prekratit' svoe sushestvovanie, esli tol'ko otnositel'naya skorost' potokov men'she dispersii skorostei zvezd v kazhdom potoke, t. e. esli v_R < v_I

Chislennyi eksperiment pokazal, chto deistvitel'no pri -maloi otnositel'noi skorosti potokov sistema zvezd raspadaetsya na otdel'nye sgusheniya.

Pri bol'shih otnositel'nyh skorostyah, t. e. pri bol'shih znacheniyah v_R / v_I, neustoichivost' takzhe proyavlyaetsya, no u nee teper' drugoi vid - vmesto otdel'nyh besporyadochnyh sgushenii poyavlyaetsya nechto vrode voloknistoi struktury, vytyanutoi vdol' osi dvizheniya potokov.

Lyubopytno napomnit', chto otkrytie asimmetrii dispersiya skorostei zvezd eshe v konce proshlogo veka privelo k poyavleniyu dvuh predstavlenii o dvizhenii zvezd v Galaktike. Soglasno odnomu iz nih, teper' obsheprinyatomu, imeetsya centroid zvezd, obrashayushiisya vokrug centra Galaktiki, i po otnosheniyu k etomu centroidu pekulyarnye skorosti zvezd raspredeleny soglasno neizotropnomu, ellipsoidal'nomu shvarcshil'dovskomu raspredeleniyu. Soglasno drugomu predstavleniyu, ranee ochen' populyarnomu, v Galaktike imeetsya dva vzaimopronikayushih potoka zvezd, i nablyudaemaya funkciya raspredeleniya skorostei sootvetstvuet nalozheniyu dvuh maksvellovskih raspredelenii. Teper' yasno, chto takaya sistema neustoichiva i dolzhna raspast'sya.

Eshe odno zamechanie po etomu povodu. Chasto rassmatrivalos' "stolknovenie" galaktik i pri etom utverzhdalos', chto v silu togo, chto zvezdnaya plotnost' ochen' mala, dve stolknuvshiesya galaktiki proidut drug cherez druga pochti bez vozmushenii, esli tol'ko ne uchityvyat' vzaimodeistvie mezhzvezdnoi sredy v etih galaktikah. Teper' my znaem, chto effekt puchkovoi neustoichivosti privedet k polnomu razrusheniyu obeih stolknuvshihsya galaktik, dazhe esli ih zvezdnaya plotnost' i ochen' mala, a mezhzvezdnogo gaza net sovsem.

Vtoraya gruppa issledovatelei, zanimavshayasya ploskimi zvezdnymi sistemami, osnovnoe vnimanie udelila modelirovaniyu spiral'nyh rukavov v diske Galaktiki [35-38]. Model' stroilas' sleduyushim obrazom. Ploskost' diska razbivalas' setkoi na 256 × 256 yacheek (v naibolee polnoi modeli). V otlichie ot predydushei gruppy issledovatelei, zdes' i prostranstvo skorostei razbivalos' na diskretnye yacheiki (vsego 63 × 63 yacheiki), prichem dvizhenie zvezd rassmatrivalos' kak perehody mezhdu centrami vseh yacheek soglasno opredelennym pravilam "igry", uchityvayushei dvizhenie chastic pod deistviem gravitacionnogo potenciala. Kak i ranee, gravitacionnyi potencial opredelyalsya metodom fur'e-preobrazovaliya po zadannomu ili opredelennomu v processe scheta raspredeleniyu poverhnostnoi plotnosti. V naibolee polnoi modeli bylo 115659 material'nyh tochek, kotorye vse imeli odinakovuyu massu.

Metod chislennogo modelirovaniya zdes' takoi zhe, kak opisannyi vyshe. V pervyh zhe raschetah avtory poluchili ochen' bystroe nagrevanie zvezdnoi sistemy. Dispersiya skorostei bystro uvelichivalas', sami zvezdy raspredelyalis' po bol'shomu ob'emu v ploskosti diska, obrazuya bystro vrashayusheesya plotnoe yadro i raspredelennoe galo. Nikakoi spiral'noi struktury v takoi sisteme ne poyavlyalos'.

Poetomu avtory prishli k vyvodu, chto dlya togo, chtoby smodelirovat' obrazovanie spiral'nyh rukavov v zvezdnoi sisteme s proizvol'nym, naprimer, odnorodnym raspredeleniem zvezdnoi plotnosti, neobhodimo kak by "ohlazhdat'" sistemu, umen'shat' dispersiyu skorostei material'nyh tochek.

Dlya etogo byla rassmotrena sleduyushaya model'. Predpolagalos', chto sistema sostoit iz zvezd i gazovyh oblakov. I te i drugie dvizhutsya v pole gravitacionnogo potenciala, rasschitannogo po raspredeleniyu polnoi plotnosti v sootvetstvii s deistvuyushimi na nih n'yutonovskimi silami. No pri rassmotrenii dvizheniya gazovyh oblakov uchityvalas' eshe odna osobennost'. Esli v processe dvizhenii v odnoi prostranstvennoi yacheike okazhutsya dva ili neskol'ko gazovyh oblakov odnovremenno (no pri etom oni raspredeleny po raznym yacheikam prostranstva skorostei), to schitaetsya, chto oblaka zdes' neuprugo stalkivayutsya i teryayut svoyu anergiyu. Inymi slovami, skorosti oblakov posle etogo shaga vychislyayutsya s usloviem sohraneniya impul'sa i momenta impul'sa, no s poterei energii na vnutrennie stepeni svobody oblaka (predpolagaetsya, chto eta energiya zatem vysvechivaetsya). Etot effekt privodit k sushestvennomu ohlazhdeniyu sistemy.

Uchityvalas' takzhe vozmozhnost' prevrasheniya gazovyh oblakov v zvezdy. Predpolagalos', chto chislo vnov' obrazovavshihsya zvezd v dannoi fazovoi yacheike proporcional'no kvadratu chisla gazovyh oblakov v etoi yacheike. Koefficient proporcional'nosti vybiralsya malym, ot 1/1000 do 1/500. Kak primer, otmetim, chto v naibolee polnom raschete iz 115659 gazovyh oblakov v konce koncov obrazovalos' 99523 zvezdy.

Zadavalas' takzhe nachal'naya skorost' vrasheniya diska, kotoraya vybiralas' libo iz usloviya balansa mezhdu centrobezhnoi siloi i gravitacionnym prityazheniem, libo schitalos', chto centrobezhnaya sila v dva raza men'she gravitacionnoi (chtoby poluchit' bolee bystryi effekt gravitacionnoi evolyucii).

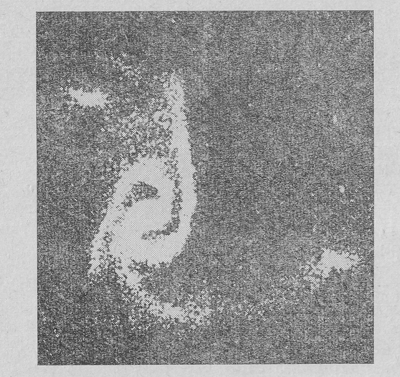
Ris. 36. Chislennoe modelirovanie obrazovaniya spiral'nyh rukavov (kadry iz fil'ma) .

Bylo provedeno neskol'ko raschetov, iz kotoryh odin dal naibolee polnye rezul'taty. Posledovatel'nost' polozhenii zvezd i gazovyh oblakov v takoi chislennoi modeli byla smontirovana v vide fil'ma, kotoryi ochen' naglyadno pokazyvaet evolyuciyu vrashayushegosya zvezdno-gazovogo diska. Kadry iz etogo fil'ma privedeny na ris. 36, 37. Kachestvenno kartiny soglasuyutsya, hotya nado otmetit' sleduyushee sushestvennoe obstoyatel'stvo - v chislennom raschete ni odin spiral'nyi rukav ne sohranyalsya bol'she treh oborotov, v to vremya kak v real'nyh galaktikah spiral'nye rukava sohranyayutsya gorazdo dol'she.

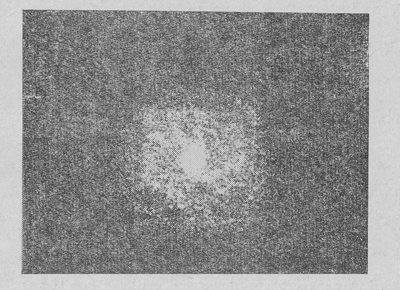
Ris. 37. Chislennoe modelirovanie obrazovaniya spiral'nyh rukavov (kadry iz fil'ma) .

Krome togo, v chislennoi modeli spiral'nuyu strukturu pokazyvayut tol'ko tochki, imitiruyushie "gazovye oblaka". Zvezdnyi fon po-prezhnemu yavlyaetsya ravnomerno nagretym "gazom chastic". V deistvitel'nosti spiral'nye rukava zatragivayut i ploskuyu sostavlyayushuyu zvezdnogo fona. V chislennom, eksperimente dispersiya skorostei zvezd v neskol'ko raz bol'she, chem v real'nyh ploskih zvezdnyh sistemah. Etot rezul'tat naglyadno proyavlyaetsya na ris. 38, gde pokazany krugovaya skorost' vrasheniya diska i uglovye skorosti gazovoi i zvezdnoi komponent. Vidno, chto uglovaya skorost' centroida zvezd v dva raza men'she uglovoi skorosti vrasheniya diska, chto i sootvetstvuet bol'shoi dispersii skorostei zvezd. Sleduet takzhe otmetit', chto dlya poyavleniya spiral'noi struktury v opisyvaemom chislennom: eksperimente byla neobhodima nekotoraya nachal'naya asimmetriya diska. V real'nyh galaktikah takaya asimmetriya mogla byt' svyazana s sushestvovaniem barov.

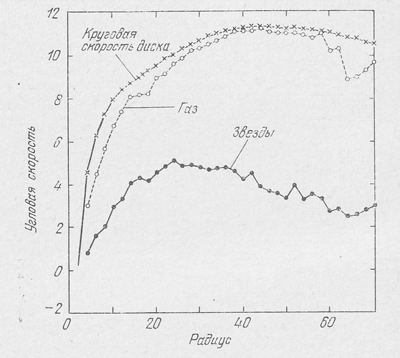
Ris. 38. Krugovaya skorost' dvizheniya diska i uglovye skorosti ego gazovoi i zvezdnoi komponent v chislennom eksperimente.

Dal'neishee razvitie chislennogo modelirovaniya spiral'noi struktury provedeno v rabote Hokneya i Braunriga [42]. Vo-pervyh, v nei bylo uchteno vliyanie naseleniya II tipa. Dlya etogo v vyrazhenie dlya potenciala (7.75) dobavlyaetsya postoyannyi vo vremeni potencial, sozdannyi sfericheskimi podsistemami naseleniya II tipa. Dalee raschet provoditsya tem zhe metodom, prichem rasschitany modeli s razlichnym procentnym sostavom naseleniya II tipa. Pokazano, chto s uvelicheniem doli etogo naseleniya stabilizaciya diska po otnosheniyu k raspadu uvelichivaetsya, i esli dolya naseleniya II tipa sostavlyaet 80%, to disk okazyvaetsya ustoichivym i obrazuyutsya dolgozhivushie dvuhrukavnye i mnogorukavnye spirali. Vo-vtoryh, v etoi rabote rassmatrivalis' i diski konechnoi tolshiny. Metod rascheta v principe prezhnii, tol'ko teper' prostranstvo diska razbivalos' na trehmernuyu setku (chislo yacheek 32 × 32 × 16, rassmatrivalos' dvizhenie 25000 zvezd). Bylo pokazano, chto trehmernyi disk stabiliziruetsya i spiral'nye rukava okazyvayutsya bolee ustoichivymi. Avtory raboty [42] nashli, chto spiral'nye rukava v zvezdnoi sisteme obrazuyutsya i bez "ohlazhdeniya" sistemy - v protivopolozhnost' rezul'tatam Millera, Prendergasta i Kvirka [36].

V rabote N. N. Kozlova, R. A. Syunyaeva i T. M. Eneeva [39] obrazovanie spiral'noi struktury galaktik svyazyvalos' s prilivnym deistviem odnoi galaktiki na druguyu. Pravda, hotya spiral'naya struktura, nesomnenno, yavlyaetsya vnutrennim svoistvom, vrashayushegosya diska galaktiki, vozmozhno, chto prilivnoe deistvie so storony drugih blizkih galaktik mozhet sozdavat' svoyu spiral'nuyu strukturu ili kak-to izmenyat' vrashenie i formu diska. Chislennaya model' prilivnogo vzaimodeistviya galaktik, postroennaya v rabote [39], zaklyuchaetsya v sleduyushem. Vokrug yadra galaktiki po krugovym orbitam vrashayutsya 800 v odnih variantah i 2000 v drugih variantah ne vzaimodeistvuyushih mezhdu soboi tel (sputnikov). Vrashenie proishodit v odnoi ploskosti i v odnom napravlenii. Zatem mimo etoi sistemy na nebol'shom rasstoyanii propuskaetsya vtoroe telo s massoi, ravnoi masse yadra galaktiki. Rassmotreny raznye varianty dvizheniya vozmushennogo tela - perpendikulyarno i parallel'no ploskosti galaktiki, v pryamom i obratnom napravlenii po otnosheniyu k ee vrasheniyu. Prohozhdenie vozmushennogo tela iskazhaet krugovye orbity i privodit k poyavleniyu dvizheniya spiraleobraznoi formy. Rezul'taty rascheta predstavleny takzhe v vide fil'ma, otdel'nye kadry iz kotorogo vosproizvedeny na ris. 39. Chetko vidna spiral'naya struktura, sohranyayushayasya v techenie neskol'kih oborotov posle prohozhdeniya vozmushennogo tela.

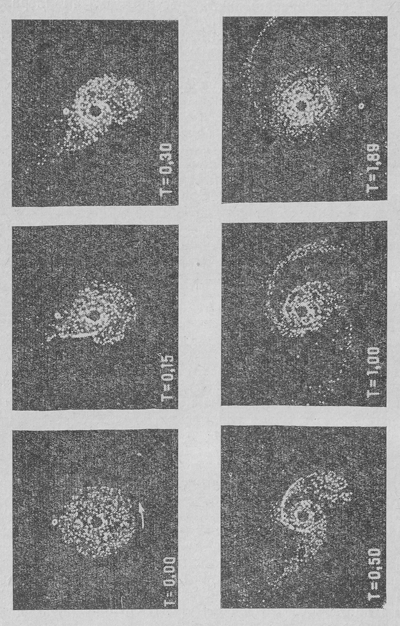
Ris. 39. Obrazovanie spiral'nyh rukavovo vo vrashayushihsya sistemah pod vliyaniem prilivnogo vzaimodeistviya (kadry iz fil'ma) .

Zadacha rassmatrivalas' v trehmernom, prostranstve, i bylo smodelirovano iskazhenie ploskosti galaktiki pod deistviem prilivnogo vzaimodeistviya. Kak izvestno, ploskost' diska mezhzvezdnoi sredy v nashei Galaktike deistvitel'no iskrivlena i eto yavlenie chasto pripisyvayut prilivnomu vozdeistviyu so storony Magellanovyh Oblakov. V rabote [39] polucheno takzhe, chto dovol'no mnogo tel (do 12%) vyryvaetsya voobshe iz galaktiki pri prohozhdenii vozmushennogo tela. Tem samym chislenno promodelirovano obrazovanie "mostov" mezhdu galaktikami.

V rabote [40] metodom chislennogo modelirovaniya rassmatrivalis' uploshennye sistemy, gde uchityvalos' i vliyanie tolshiny diska. Reshalas' sistema (7.1) no s potencialom (7.62). Chislo zvezd v raznyh variantah - ot 150 do 500. Osnovnaya cel' chislennogo eksperimenta zaklyuchalas' v izuchenii ustoichivosti i evolyucii sistemy v zavisimosti ot otnosheniya kineticheskoi energii vrasheniya k polnoi gravitacionnoi energii. Esli zadavat' nekotoruyu nachal'nuyu konfiguraciyu trehmernoi vrashayusheisya zvezdnoi sistemy, to v processe evolyucii vsegda uvelichivaetsya dispersiya skorostei i odnovremenno umen'shaetsya srednyaya skorost' vrasheniya sistemy. Poetomu otnoshenie srednei kineticheskoi energii sistematicheskogo dvizheniya zvezd, t. e. kineticheskoi energii "chistogo" vrasheniya k gravitacionnoi energii dolzhno vse vremya umen'shat'sya. V rabote [40] pokazano metodom chislennogo eksperimenta, chto eto otnoshenie stremitsya k 0,14 nezavisimo ot vybora ryada nachal'nyh uslovii.

V rabote [40] otmechaetsya takzhe, chto rezul'tat dannogo chislennogo eksperimenta (voobshe govorya, soglasuyushegosya .i s drugimi chislennymi eksperimentami i pokazyvayushego, chto vo vrashayusheisya zvezdnoi sisteme v kvaziravnovesnom sostoyanii kineticheskaya energiya sistematicheskogo dvizheniya zvezd, t. e. vrasheniya ne bol'she 14% ot polnoi gravitacionnoi energii) protivorechit nablyudatel'nym dannym. V nashei Galaktike orbity zvezd pochti krugovye, i kineticheskaya energiya dvizheniya zvezd po approksimacionnym krugovym orbitam, sostavlyaet sushestvenno bol'shuyu dolyu ot gravitacionnoi energii. Rashozhdenie mozhet byt' udastsya ustranit' uchetom roli sfericheskih podsistem Galaktiki (galo Galaktiki)

Kollaps i burnaya relaksaciya vrashayushihsya zvezdnyh sistem metodom chislennogo modelirovaniya byli issledovany v rabote [41].

<< § 7.5 Chislennoe modelirovanie evolyucii zvezdnyh skoplenii | Oglavlenie | § 8.1 Struktura kvazarov i yader galaktik >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce