Astronet > Razmernosti i podobie astrofizicheskih velichin

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Razmernosti i podobie astrofizicheskih velichin << § 8.1 Struktura kvazarov i yader galaktik | Oglavlenie | § 8.3 Osnovnye parametry Metagalaktiki >>

§ 8.2 Gravitacionnaya neustoichivost'

Vozniknovenie zvezd i drugih nebesnyh tel vozmozhno tol'ko potomu, chto v mire sushestvuet gravitaciya. Ob etom, pisal eshe N'yuton v pis'me k Bentli v 1692 g. Ideya N'yutona byla oformlena fizicheski i matematicheski Dzhinsom v ego izvestnoi knige "Astronomiya i kosmogoniya" [10]. Sushnost' mehanizma N'yutona-Dzhinsa, ili mehanizma gravitacionnoi neustoichivosti, zaklyuchaetsya v sleduyushem.

Vo vsyakom gaze vsegda imeyutsya fluktuacii plotnosti, voznikayushie pri haoticheskom, dvizhenii sostavlyayushih gaz atomov ili molekul. Eti fluktuacii vonikayut i raspadayutsya, prichem dinamika fluktuacii opredelyaetsya odnim parametrom - temperaturoi.

Situaciya sushestvenno izmenitsya, esli my, krome temperatury, rassmotrim, drugoi faktor - tyagotenie. Dlya malyh masshtabov gravitaciya ne sushestvenna. Dlya bol'shih masshtabov mozhet sluchit'sya, chto sobstvennoe prityazhenie takoi fluktuacii okazhetsya sposobnye uderzhat' gaz v dannom ob'eme i ne dat' emu rasseyat'sya. Sila tyagoteniya narastaet s uvelicheniem massy, a teplovye svoistva sredy ne zavisyat ot razmera. V etih usloviyah vozmozhno razbienie pervonachal'no odnorodnoi sredy na sgustki s nekotorym harakternym masshtabom, nazyvaemym dzhinsovskoi dlinoi.

Ocenku dzhinsovskoi, ili kriticheskoi, dliny mozhno sdelat' sleduyushim obrazom. Sravnim teplovuyu energiyu sgusheniya (fluktuacii) s ego gravitacionnoi energiei. Gravitacionnaya energiya na edinicu massy

$F_g \approx \frac{GM}{\lambda} \approx G\rho\lambda^2,$ (8.12)

gde λ - harakternyi razmer sgusheniya. Teplovaya energiya na edinicu massy est'

$E_T \approx \frac{\Re T}{\mu}.$ (8.13)

Priravnivaya eti dve velichiny, poluchim vyrazhenie dlya kriticheskoi dliny volny

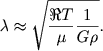
$\lambda \approx \sqrt{\frac{\Re T}{\mu}\frac{1}{G\rho}}.$ (8.14)

Mozhno poluchit' formulu Dzhinsa i iz soobrazhenii razmernosti. Opredelyayushie parametry zadachi takovy. Gravitacionnye svoistva sredy zadayutsya srednei plotnost'yu ρ i postoyannoi tyagoteniya G. Teplovye svoistva zavisyat ot temperatury, universal'noi gazovoi postoyannoi i molekulyarnogo vesa. Eti faktory my sgruppiruem vmeste. Togda imeem matricu razmernosti:

$\begin{matrix} \, & [\lambda] & [G] & [\rho] & [\frac{\Re T}{\mu}] \\ \mbox{g}&0&-1&1&0 \\ \mbox{sm}&1&3&-3&2 \\ \mbox{sek}&0&-2&0&-2 \end{matrix}$

Reshenie matricy daet edinstvennyi bezrazmernyi kompleks, takzhe privodyashii k formule (8.14) s tochnost'yu do nekotorogo bezrazmernogo mnozhitelya. Obychno vyrazhayut temperaturu cherez izotermicheskuyu skorost' zvuka:

$v^2_s = \frac{\Re T}{\mu}.$ (8.15)

Bezrazmernaya postoyannaya ravna π^½, i my poluchaem, formulu Dzhinsa v ee obychnom vide:

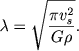
$\lambda = \sqrt{\frac{\pi v_s^2}{G\rho}}.$ (8.16)

Ponyatie gravitacionnoi neustoichivosti imeet prostoi fizicheskii smysl. Ustoichivost' lyuboi sistemy proveryaetsya nalozheniem na sistemu malyh kolebanii. Esli kolebaniya zatuhayut, sistema ustoichiva, esli oni nachinayut rasti - neustoichiva. Vvidu nalichiya gravitacii kolebaniya gaza v bol'shih masshtabah nazyvayut "tyazhelym zvukom" (sm. gl. 7). Kolebaniya s men'shei dlinoi volny zatuhayut, tak kak v nih teplovaya energiya bol'she gravitacionnoi; kolebaniya s bol'shei dlinoi volny - neustoichivy. Perehod sredy iz ustoichivogo sostoyaniya v neustoichivoe legko ponyat', esli vspomnit', chto pri malyh plotnostyah kosmicheskii gaz pochti vsegda prozrachen. Pri postepennom ostyvanii temperatura ponizhaetsya i sreda stanovitsya gravitacionno neustoichivoi.

V sootnosheniyah (8.14) - (8.16) ne rassmatrivaetsya dinamika raspada na sgusheniya, a nahoditsya tol'ko kriterii gravitacionnoi neustoichivosti, strogo spravedlivye dlya sluchaya, kogda ishodnaya sreda v nachal'nyi moment vremeni pokoitsya. Takaya vazhnaya dlya kosmologii zadacha, kak raspad na sgusheniya rasshiryayusheisya sredy, byla reshena vpervye E. M. Lifshicem (podrobnosti sm. [2]), kotoryi uchel zavisimost' nachal'noi plotnosti ot vremeni. Vprochem, okazalos', chto rezul'taty Dzhinsa s ochen' nebol'shimi popravkami ostayutsya spravedlivymi i v etom sluchae, esli prinimat' dlya $\bar\rho$ mgnovennoe znachenie plotnosti v moment raspada sredy.

Teper' prosledim dal'neishuyu sud'bu gravitacionnyh konfiguracii. Massy kondensacii, "obrazuyushihsya v tyazhelom zvuke, poryadka

$M \approx \rho\lambda^3 \approx \left(\frac{\pi}{G}\right)^{3/2}\frac{v_s^3}{\rho^{1/2}},$ (8.17)

gde v_s - harakternaya skorost'. V prosteishem sluchae eto skorost' zvuka, no voobshe ona mozhet otrazhat' i nalichie drugih faktorov (vrashenie, turbulentnost', skorost' al'venovokih voln). Minimal'noe znachenie M opredelyaetsya gazovym i luchistym davleniem. Poetomu minimal'naya massa kondensacii

$M \approx \rho\lambda^3 \approx \left(\frac{\pi}{G}\right)^{3/2}\frac{v_s^3}{\rho^{1/2}},$ (8.18)

V nastoyashee vremya minimal'naya temperatura kosmicheskoi sredy ravna 3ś. V proshlom temperatury byli vyshe. V zavisimosti ot hoda izmeneniya plotnosti i temperatury dlya konkretnyh modelei, massy obrazuyushihsya kondensacii okazyvayutsya razlichnymi. Kondensacii v volnah "tyazhelogo zvuka" sobirayut veshestvo, ostavsheesya vne sgusheniya. Harakternoe vremya takogo sobiraniya mozhno ocenit', podstavlyaya v formulu akkrecii (2.30) vmesto massy zvezdy massu obrazovavshihsya sgushenii (8.17). Togda dlya otnositel'nogo izmeneniya massy imeem

$\frac{1}{M}\frac{dM}{dt} \approx (2\pi)^{5/2}(G\rho)^{1/2}.$

Harakternoe vremya zdes' sravnimo (neskol'ko men'she) so vremenem, svobodnogo padeniya. Takim obrazom, obrazovavshiesya kondensacii bystro sobirayut bol'shuyu chast' "neispol'zovannoi massy" i zatem nachinayut szhimat'sya, obrazuya protozvezdy, protogalaktiki i t.d.

Otmetim eshe odno obstoyatel'stvo. V formule Dzhinsa net kakoi-libo fundamental'noi dliny, opredelyaemoi atomnymi ili kakimi-libo drugimi konstantami. Poetomu, esli imeetsya nepreryvnyi ryad izmeneniya nachal'nyh parametrov sredy - plotnosti i temperatury-my poluchim sploshnoi spektr dlin voln neustoichivosti. Ne isklyucheno, chto nepreryvnyi ryad harakternyh razmerov nebesnyh tel - zvezdnyh skoplenii, galaktik, skoplenii galaktik - est' svidetel'stvo togo, chto v proshlom vo Vselennoi imel mesto process gravitacionnoi kondensacii.

Obsudim teper', posle vyyasneniya obshego fizicheskogo smysla mehanizma gravitacionnoi neustoichivosti, nekotorye dopolnitel'nye soobrazheniya. Rassmotrim ploskuyu sistemu, naprimer, vrashayushuyusya galaktiku. V etom sluchae vmesto ob'emnoi plotnosti my dolzhny vvesti poverhnostnuyu plotnost' massy

$[\rho_s] = \mbox{g} \cdot \mbox{sm}^{-2}.$

V etom sluchae kriterii Dzhinsa priobretaet vid

$\lambda = 2\pi\frac{v_s^2}{G\rho_s}.$ (8.19)

Eta formula poluchena Ledu [11]. Zdes' λ - tolshina gravitacionno-ustoichivogo sloya ili diska. Etoi formuloi mozhno ob'yasnit' izvestnyi iz radionablyudenii fakt utolsheniya gazovogo diska Galaktiki ot centra k periferii. Tolshina diska svyazana s plotnost'yu, i po mere ubyvaniya plotnosti k periferii tolshina diska rastet.

Dalee, esli obrazuyushiesya sgusheniya vrashayutsya, naprimer iz-za nesimmetrichnosti v nachal'nyi moment, to pri szhatii uglovaya skorost' uvelichivaetsya v sootvetstvii s teoremoi sohraneniya uglovogo momenta. Togda uslovie, trebuyushee, chtoby sgushenie ne razletelos' iz-za vrasheniya, imeet vid

$G\rho \lesssim (\Delta\Omega)^2,$ (8.20)

gde ΔΩ;;; - izmenenie uglovoi skorosti v predelah rassmatrivaemogo sgusheniya.

Vopros o vrashenii kondensacii (protogalaktik) mozhno rassmotret' s drugoi storony. Pust' my imeem vydelivshuyusya v rezul'tate dzhinsovskoi neustoichivosti kondensaciyu s vrasheniem. Ona harakterizuetsya sleduyushimi parametrami: massoi, vrashatel'nym momentom, postoyannoi tyagoteniya (kondensaciya gravitacionno svyazana), i temperaturoi, kotoruyu budem vyrazhat' cherez skorost' zvuka. Naidem zavisimost' mezhdu etimi faktorami. Matrica razmernosti

$\begin{matrix} \, & [v_s] & [\mathfrak{M}] & [G] & [M] \\ \mbox{g}&0&1&-1&1 \\ \mbox{sm}&1&2&3&0 \\ \mbox{sek}&-1&-1&-2&0 \end{matrix}$

daet edinstvennyi bezrazmernyi kompleks, otkuda sleduet formula

$\mathfrak{M} = const \cdot \frac{GM^2}{v_2}$ (8.21)

Postoyannaya soglasno [12] ravna 12/5 π . Analogichnaya formula dlya relyativistskogo diska $\mathfrak{M} \approx \frac{GM^2}{c}$ byla vyvedena Vagonerom [13]. Kak uzhe otmechalos' v gl. 7, nablyudatel'nye dannye luchshe vsego sootvetstvuyut zavisimosti $\mathfrak{M} \sim M^{7/4}$ . Drugie avtory poluchali blizkie zavisimosti $\mathfrak{M} \sim M^{2}$ i $\mathfrak{M} \sim M^{5/3}$ (sm. [14]), tak chto mozhno schitat' sootnoshenie (8.21)) priblizhenno vernym.

Itak, esli galaktika "pomnit" nachal'nye usloviya svoego obrazovaniya i zavisimost' $\mathfrak{M} \sim M^2$ mozhno rassmatrivat' kak rezul'tat gravitacionnoi neustoichivosti, to mozhno sdelat' popytku ocenit' temperaturu sredy, iz kotoroi obrazovalis' galaktiki. Pust' v nekotoroi dostatochno blizkoi okrestnosti nashego Mlechnogo Puti temperatura i tem samym velichina bj odinakovy. Chislennyi koefficient zavisimosti $\mathfrak{M}$ ot M mozhno opredelit' iz nablyudenii (sm. ris. 26). Togda iz (8.21) nahodim v_s ≈ 3,5 ⋅ 10⁶ sm/sek. Esli eta skorost' est' obychnaya skorost', to T ≈ 10⁶ K. Etu velichinu mozhno, po-vidimomu, rassmatrivat' kak opredelennuyu iz nablyudenii.

Obsudim teper' effekty magnitnogo polya. Magnitnoe pole, kak i upomyanutoe ranee vrashenie, faktor sushestvenno anizotropnyi. Magnitnoe pole prepyatstvuet szhatiyu v napravlenii, perpendikulyarnom k silovym liniyam. Vdol' etih linii pole ne tol'ko ne prepyatstvuet szhatiyu, no i sposobstvuet emu (neustoichivost' Pikel'nera - Parkera).

Dlya kolichestvennyh ocenok mozhno schitat' harakternoi skorost'yu skorost' al'venovskih voln

$v_A = \frac{H}{\sqrt{4\pi \rho}}$ (8.22)

ili sravnivat' gravitacionnoe i magnitnoe davleniya

$G\rho^2\lambda^2 \approx \frac{H^2}{8\pi}.$ (8.23)

Na rannih stadiyah evolyucii Vselennoi magnitnoe davlenie mozhet prevoshodit' davlenie gaza, i v etih usloviyah vliyanie magnitnogo polya na process obrazovaniya galaktik mozhet okazat'sya sushestvennym. Hotya nablyudatel'nye dannye po dalekim radiogalaktikam eshe ne dayut odnoznachnyh vyvodov o nalichii i velichine polya, ego sushestvovanie v principe ne isklyucheno. V chastnosti, magnitnoe pole moglo by ob'yasnit' lyubopytnyi fakt vystraivaniya galaktik cepochkami. V etom sluchae estestvenno predpolagat' gravitacionnuyu neustoichivost' nekotoroi cilindricheskoi konfiguracii, obrazovavsheisya pod deistviem magnitnogo polya. Gravitacionnaya neustoichivost' kosmologicheskih modelei s pervichnym magnitnym polem, privodyashaya k obrazovaniyu diskovyh (dvumernyh) i nitevidnyh (odnomernyh) obrazovanii, rassmatrivalas' v rabote [15].

Itak, v obshem sluchae dlya sgusheniya, vydelivshegosya iz pervichno odnorodnoi sredy blagodarya mehanizmu gravitacionnoi neustoichivosti, mozhno zapisat' uslovie ravnovesiya

$G\rho^2\lambda^2 \approx \rho(v_R^2 + \langle v \rangle^2) + \frac{H^2}{8\pi} + p_{\mbox{gaz}} + p_{\mbox{luch}},$ (8.24)

gde v_R - vrashatel'naya skorost', 〈v〉 - turbulentnaya skorost'. V takoi formulirovke uslovie ravnovesiya (8.24), kak mozhno videt', ekvivalentno izvestnoi teoreme viriala.

<< § 8.1 Struktura kvazarov i yader galaktik | Oglavlenie | § 8.3 Osnovnye parametry Metagalaktiki >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce