Obshaya teoriya otnositel'nosti
12.12.2005 21:11 | "Sorosovskaya Enciklopediya"
1. Nemnogo istorii
Obshaya teoriya otnositel'nosti (OTO) – sovremennaya teoriya tyagoteniya, svyazyvayushaya ego s kriviznoi chetyrehmernogo prostranstva-vremeni.
B svoem klassicheskom variante teoriya tyagoteniya byla sozdana Isaakom N'yutonom eshe v XVII veke i do sih por verno sluzhit chelovechestvu. Ona vpolne dostatochna dlya mnogih, esli ne dlya bol'shinstva zadach sovremennoi astronomii, astrofiziki, kosmonavtiki. Mezhdu tem ee principial'nyi vnutrennii nedostatok byl yasen eshe samomu N'yutonu. Eto teoriya s dal'nodeistviem: v nei gravitacionnoe deistvie odnogo tela na drugoe peredaetsya mgnovenno, bez zapazdyvaniya. N'yutonovskaya gravitaciya tak zhe sootnositsya s obshei teoriei otnositel'nosti, kak zakon Kulona s maksvellovskoi elektrodinamikoi. Dzh.K. Maksvellu udalos' izgnat' dal'nodeistvie iz elektrodinamiki. V gravitacii eto sdelal Al'bert Einshtein.
V 1905 godu A. Einshtein sformuliroval special'nuyu teoriyu otnositel'nosti, kotoraya zavershila v ideinom otnoshenii razvitie klassicheskoi elektrodinamiki. V stat'yah predshestvennikov Einshteina H.A. Lorenca i Zh.A. Puankare soderzhalis' mnogie elementy special'noi teorii otnositel'nosti, odnako cel'naya kartina fiziki bol'shih skorostei poyavilas' lish' v rabote Einshteina.
Sozdanie sovremennoi teorii tyagoteniya bylo nemyslimo bez special'noi teorii otnositel'nosti, bez glubokogo ponimaniya struktury klassicheskoi elektrodinamiki, bez osoznaniya edinstva prostranstva-vremeni. Ochen' veliko dlya OTO znachenie matematiki. Ee apparat, tenzornyi analiz, ili absolyutnoe differencial'noe ischislenie, byl razvit G. Richchi i T. Levi-Chivita.
I vse zhe OTO – eto fizicheskaya teoriya, v osnove kotoroi lezhit yasnyi fizicheskii princip, tverdo ustanovlennyi eksperimental'nyi fakt.
2. Princip ekvivalentnosti i geometrizaciya tyagoteniya
G. Galilei ustanovil: vse tela dvizhutsya v pole tyazhesti (pri otsutstvii soprotivleniya sredy) s odinakovym uskoreniem, traektorii vseh tel s zadannoi skorost'yu iskrivleny v gravitacionnom pole odinakovo. Blagodarya etomu v svobodno padayushem lifte nikakoi eksperiment ne mozhet obnaruzhit' gravitacionnoe pole, inymi slovami, v svobodno dvizhusheisya v gravitacionnom pole sisteme otscheta v maloi oblasti prostranstva-vremeni gravitacii net. Poslednee utverzhdenie – eto odna iz formulirovok principa ekvivalentnosti.
Dannoe svoistvo polya tyagoteniya otnyud' ne trivial'no. V sluchae elektromagnitnogo polya situaciya sovershenno inaya. Sushestvuyut, naprimer, nezaryazhennye neitral'nye tela, kotorye elektromagnitnogo polya voobshe ne chuvstvuyut. Tak vot, gravitacionno-neitral'nyh tel net, ne sushestvuet ni lineek, ni chasov, kotorye ne chuvstvovali by gravitacionnogo polya. Lyuboi etalon pryamoi, naprimer luch sveta, ne obladaet v pole tyagoteniya svoistvami pryamoi linii. Net ob'ektov, kotorye v etom pole mozhno bylo by otozhdestvit' s pryamymi, kak v evklidovoi geometrii. Poetomu geometriyu nashego prostranstva estestvenno schitat' neevklidovoi.
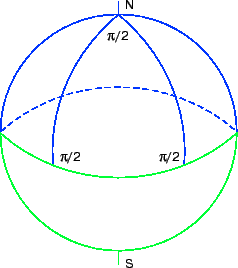
Nekotoroe predstavlenie o svoistvah takogo prostranstva mozhno poluchit' na prosteishem primere sfery, poverhnosti obychnogo globusa. Rassmotrim na nei sfericheskii treugol'nik, figuru, ogranichennuyu dugami bol'shogo kruga. (Duga bol'shogo kruga, soedinyayushaya dve tochki na sfere, – eto kratchaishee rasstoyanie mezhdu nimi; ona predstavlyaet soboi estestvennyi analog pryamoi na ploskosti.) Vyberem v kachestve etih dug uchastki meridianov, otlichayushihsya na 90° po dolgote, i ekvatora (ris. 1). Summa uglov etogo sfericheskogo treugol'nika ne ravna π – summe uglov treugol'nika na ploskosti:
| α+β+γ =1,5π. | (1) |
Prevyshenie summy uglov dannogo treugol'nika nad π mozhet byt' vyrazheno cherez ego ploshad' S i radius sfery R:
| α+β+γ-π =S/R 2. | (2) |
Eto sootnoshenie spravedlivo dlya lyubogo sfericheskogo treugol'nika. Obychnyi sluchai treugol'nika na ploskosti takzhe vytekaet iz etogo ravenstva: ploskost' mozhno rassmatrivat' kak sferu s R→∞. Esli perepisat' formulu (2) inache:
| K=1/R 2=[α+β+γ-π]/S, | (3) |
to vidno, chto radius sfery mozhno opredelit', ostavayas' na nei, ne obrashayas' k trehmernomu prostranstvu, v kotoroe ona pogruzhena. Dlya etogo dostatochno izmerit' ploshad' sfericheskogo treugol'nika i summu ego uglov. Inymi slovami, R ili K yavlyayutsya vnutrennei harakteristikoi sfery. Velichinu K prinyato nazyvat' gaussovoi kriviznoi, ona estestvennym obrazom obobshaetsya na proizvol'nuyu gladkuyu poverhnost':
| K(x)=limS→∞[α+β+γ-π]/S. | (4) |
Zdes' ugly i ploshad' otnosyatsya k malomu treugol'niku na poverhnosti, ogranichennomu liniyami kratchaishih rasstoyanii na nei, a krivizna, voobshe govorya, menyaetsya ot tochki k tochke, to est' yavlyaetsya velichinoi lokal'noi. V obshem sluchae, tak zhe kak i dlya sfery, parametr K sluzhit vnutrennei harakteristikoi poverhnosti, ne zavisyashei ot ee pogruzheniya v trehmernoe prostranstvo. Gaussova krivizna ne menyaetsya pri izgibanii poverhnosti bez ee razryva i rastyazheniya. Tak, naprimer, konus ili cilindr mozhno razognut' v ploskost', i poetomu dlya nih, tak zhe kak dlya ploskosti, K=0.
Esli vzyat' na polyuse (ris. 1) vektor, napravlennyi vdol' odnogo iz meridianov, perenesti ego vdol' etogo meridiana, ne menyaya ugla mezhdu nimi (v dannom sluchae nulevogo), na ekvator, dalee, perenesti ego vdol' ekvatora, snova ne menyaya ugla mezhdu nimi (na sei raz π/2), na vtoroi meridian, nakonec takim zhe obrazom vernut'sya vdol' vtorogo meridiana na polyus, to v otlichie ot takogo zhe perenosa po zamknutomu konturu na ploskosti vektor okazhetsya povernutym otnositel'no svoego ishodnogo napravleniya na π/2 ili na
| α+β+γ-π =KS. | (5) |
Etot rezul'tat – povorot vektora pri ego perenose vdol' zamknutogo kontura na ugol, proporcional'nyi ohvachennoi ploshadi, – estestvennym obrazom obobshaetsya ne tol'ko na proizvol'nuyu dvumernuyu poverhnost', no i na mnogomernye neevklidovy prostranstva. Odnako v obshem sluchae n-mernogo prostranstva krivizna ne svoditsya k odnoi skalyarnoi velichine K(x) . Eto bolee slozhnyi geometricheskii ob'ekt, imeyushii n2(n2-1)/12 komponent. Ego nazyvayut tenzorom krivizny ili tenzorom Rimana, a sami eti prostranstva – rimanovymi. V chetyrehmernom rimanovom prostranstve-vremeni obshei teorii otnositel'nosti tenzor krivizny imeet 20 komponent.
3. Klassicheskie opyty po proverke OTO
V nachale predydushego razdela uzhe otmechalos', chto gravitacionnoe pole vliyaet na dvizhenie ne tol'ko massivnyh tel, no i sveta. V chastnosti, foton, rasprostranyayas' v pole Zemli vverh, sovershaet rabotu protiv sily tyazhesti i poetomu teryaet energiyu (sm., odnako, rabotu [6]). Kak izvestno, energiya fotona proporcional'na ego chastote, kotoraya tozhe padaet. Etot effekt – krasnoe smeshenie – byl predskazan Einshteinom eshe v 1907 godu. Netrudno ocenit' ego velichinu. Rabota protiv sily tyazhesti, ochevidno, proporcional'na gh, gde g – uskorenie svobodnogo padeniya, a h – vysota pod'ema. Proizvedenie gh imeet razmernost' kvadrata skorosti. Poetomu rezul'tat dlya otnositel'nogo smesheniya chastoty iz soobrazhenii razmernosti takov:
| δω/ω=gh/c2, | (6) |
gde c – skorost' sveta. Pri g ≈10 m/s2, h≈10 m otnositel'noe smeshenie nichtozhno malo: ~10-15. Neudivitel'no, chto eksperimental'no krasnoe smeshenie udalos' nablyudat' lish' spustya polveka, s poyavleniem tehniki, ispol'zuyushei effekt Mëssbauera.
Eshe odin effekt, predskazannyi Einshteinom na zare OTO, – otklonenie lucha sveta v pole Solnca. Ego velichina ocenivaetsya sleduyushim obrazom. Esli harakternoe, pricel'noe rasstoyanie lucha ot Solnca ravno ρ, to radial'noe uskorenie sostavlyaet GM/ρ2, gde G – n'yutonovskaya gravitacionnaya postoyannaya, a M – massa Solnca. Za harakternoe vremya proleta ρ/c radial'naya komponenta skorosti fotona izmenitsya na GM/(ρc) i sootvetstvenno ugol otkloneniya sostavit
| rg =2GM/c2. | (7) |
Naivnoe ispol'zovanie poluklassicheskih soobrazhenii deistvitel'no privodit k otvetu
| θ=2rg /ρ. | (8) |
Gravitacionnyi radius Solnca rg ≈3 km, a pricel'nyi parametr estestvenno sdelat' kak mozhno blizhe k obychnomu radiusu Solnca, kotoryi sostavlyaet 7·108 m. Takim obrazom, dlya lucha sveta, prohodyashego vblizi poverhnosti Solnca, ugol otkloneniya sostavlyaet 1″,75. Izmereniya, provedennye gruppoi A.S. Eddingtona vo vremya solnechnogo zatmeniya 1919 goda, podtverdili poslednee predskazanie.
K chislu klassicheskih testov OTO otnositsya takzhe vrashenie perigeliya orbity Merkuriya. Zamknutye ellipticheskie orbity – eto specifika nerelyativistskogo dvizheniya v prityagivayushem potenciale 1/r. Neudivitel'no, chto v OTO orbity planet nezamknuty. Malyi effekt takogo roda udobno opisyvat' kak vrashenie perigeliya ellipticheskoi orbity. Zadolgo do poyavleniya OTO astronomy znali, chto perigelii orbity Merkuriya povorachivaetsya za stoletie primerno na 6000″. Povorot etot v osnovnom ob'yasnyalsya gravitacionnymi vozmusheniyami dvizheniya Merkuriya so storony drugih planet Solnechnoi sistemy. Ostavalsya, odnako, neustranimyi ostatok – okolo 40″, v stoletie. V 1915 godu Einshtein ob'yasnil eto rashozhdenie v ramkah OTO.
Iz prostyh soobrazhenii razmernosti mozhno ozhidat', chto povorot perigeliya za odin oborot sostavlyaet
| δ=3π rg /R . | (9) |
Pri radiuse orbity Merkuriya R≈0,6·1010 m eto daet 43″ v stoletie, snimaya takim obrazom sushestvovavshee rashozhdenie. Merkurii – eto planeta, blizhaishaya k Solncu, planeta s naimen'shim radiusom orbity R, poetomu vrashenie perigeliya orbity u nee maksimal'no.
4. Chernye dyry
Rol' OTO otnyud' ne svoditsya k issledovaniyu malyh popravok k obychnoi n'yutonovskoi gravitacii. Sushestvuyut ob'ekty, nazyvaemye chernymi dyrami, v kotoryh effekty OTO igrayut klyuchevuyu rol'. Eto kompaktnye zvezdy.
Eshe v XVIII veke Dzh. Mitchel i P.S. Laplas nezavisimo zametili, chto mogut sushestvovat' zvezdy, obladayushie neobychnym svoistvom: svet ne mozhet pokinut' ih poverhnost'. Rassuzhdenie vyglyadelo primerno tak. Telo, obladayushee radial'noi skorost'yu V , mozhet pokinut' poverhnost' zvezdy radiusa R i massy M pri uslovii, chto kineticheskaya energiya etogo tela mV 2/2 prevyshaet energiyu prityazheniya GMm/R, to est' pri V 2>2GM/R. Primenenie poslednego neravenstva k svetu (chto sovershenno neobosnovanno) privodit k vyvodu: esli radius zvezdy massy M men'she chem rg,
Chernaya dyra – vpolne estestvennoe nazvanie dlya takogo ob'ekta. Svoistva ego ves'ma neobychny. Chernaya dyra voznikaet, kogda zvezda szhimaetsya nastol'ko sil'no, chto usilivayusheesya gravitacionnoe pole ne vypuskaet vo vneshnee prostranstvo nichego, dazhe svet. Poetomu iz chernoi dyry ne vyhodit nikakaya informaciya.
Pri padenii probnogo tela na chernuyu dyru po chasam beskonechno udalennogo nablyudatelya ono budet dostigat' gravitacionnogo radiusa beskonechno dolgo. Odnako po chasam, ustanovlennym na samom probnom tele, vremya etogo puteshestviya vpolne konechno.
Mnogochislennye rezul'taty astronomicheskih nablyudenii dayut ser'eznye osnovaniya polagat', chto chernye dyry – eto ne prosto igra uma fizikov-teoretikov, a real'nye ob'ekty, sushestvuyushie, po krainei mere, v yadrah galaktik. Podrobnee o problemah, svyazannyh s chernymi dyrami, mozhno uznat' iz statei A.M. Cherepashuka "Chernye dyry v dvoinyh zvezdnyh sistemah" i D.A. Kirzhnica "Goryachie chernye dyry" v etom tome.
5. Pul'sar PSR 1913+16 i gravitacionnye volny
Nobelevskaya premiya po fizike za 1993 god byla prisuzhdena R.A. Halsu i Dzh.G. Teiloru za issledovanie pul'sara PSR 1913+16 (PSR oznachaet pul'sar, a cifry otnosyatsya k koordinatam na nebesnoi sfere: pryamoe voshozhdenie 19h13m, sklonenie 16°). Issledovanie svoistv izlucheniya etogo pul'sara pokazalo, chto on yavlyaetsya komponentoi dvoinoi zvezdy, inymi slovami, u nego est' kompan'on i obe zvezdy vrashayutsya vokrug obshego centra mass. Rasstoyanie mezhdu pul'sarom i ego kompan'onom sostavlyaet vsego 1,8·109 m. Esli by nevidimyi kompan'on byl obychnoi zvezdoi s harakternym radiusom ~109 m, to nablyudalis' by, ochevidno, zatmeniya pul'sara. Odnako nichego podobnogo ne proishodit. Podrobnyi analiz nablyudenii pokazal, chto nevidimaya komponenta – eto ne chto inoe, kak neitronnaya zvezda. Inymi slovami, sistema PSR 1913+16 sostoit iz dvuh neitronnyh zvezd, odna iz kotoryh imeet sil'noe ( ~1012 Gs) magnitnoe pole, to est' yavlyaetsya pul'sarom.
Sushestvovanie neitronnyh zvezd bylo predskazano teoreticheski eshe v 30-e gody. Oni obrazuyutsya v rezul'tate burnogo gravitacionnogo szhatiya massivnyh zvezd, soprovozhdayushegosya vzryvom sverhnovyh. Posle vzryva davlenie v ostavshemsya yadre massivnoi zvezdy prodolzhaet narastat', elektrony s protonami slivayutsya (s ispuskaniem neitrino) v neitrony. Obrazuetsya ochen' plotnaya zvezda s massoi, neskol'ko bol'shei massy Solnca, no ochen' malogo razmera, poryadka 10-15 kilometrov, ne prevyshayushego razmer asteroida. Nablyudenie neitronnyh zvezd uzhe samo po sebe yavlyaetsya vydayushimsya otkrytiem. Krome togo, tshatel'noe issledovanie dvizheniya dvoinoi zvezdy PSR 1913+16 dalo novoe podtverzhdenie predskazaniya OTO, kasayushegosya nezamknutosti ellipticheskih orbit. Poskol'ku gravitacionnye polya v dannoi sisteme ochen' veliki, periastr orbity vrashaetsya nesravnenno bystree, chem perigelii orbity Merkuriya, on povorachivaetsya na 4°,2 v god. Izuchenie etogo i drugih effektov pozvolilo takzhe opredelit' s vysokoi tochnost'yu massu pul'sara i neitronnoi zvezdy. Oni ravny sootvetstvenno 1,442 i 1,386Mʘ.
V 1918 godu Einshtein predskazal na osnove OTO sushestvovanie gravitacionnogo izlucheniya. Horosho izvestno, chto elektricheski zaryazhennye chasticy, buduchi uskorennymi, izluchayut elektromagnitnye volny. Analogichno, massivnye tela, dvigayas' s uskoreniem, izluchayut gravitacionnye volny – ryab' geometrii prostranstva, rasprostranyayushuyusya tozhe so skorost'yu sveta. Analogiya eta nepolna (vprochem, kak prakticheski i vsyakaya inaya). Odno iz otlichii mezhdu elektromagnitnymi i gravitacionnymi volnami, imeyushee dovol'no sushestvennyi harakter, sostoit v sleduyushem. V otlichie ot sluchaya elektromagnitnogo polya plotnost' energii gravitacionnogo polya, gravitacionnoi volny lokal'na: v dannoi tochke ee vsegda mozhno obratit' v nul' vyborom sootvetstvuyushei sistemy koordinat. Let 60-70 nazad eto obstoyatel'stvo rassmatrivalos' kak ser'eznaya trudnost' teorii. Zatem, odnako, smysl ego byl proyasnen i problema snyata. V poslednie gody vnov' poyavilis' utverzhdeniya o tom, chto vozmozhnost' obrasheniya v nul' lokal'noi plotnosti energii gravitacionnogo polya yavlyaetsya korennym, principial'nym defektom OTO.
Na samom zhe dele nichego strashnogo v etom net. Dannyi vyvod yavlyaetsya pryamym sledstviem principa ekvivalentnosti. Deistvitel'no, pri perehode v sistemu, svyazannuyu so svobodno padayushim liftom, obrashaetsya v nul' napryazhennost' gravitacionnogo polya. Estestvenno, chto v etoi sisteme ravna nulyu i plotnost' energii gravitacionnogo polya. (Eto soobrazhenie prinadlezhit S.I. Literatu, uchitelyu srednei shkoly 130 g. Novosibirska.)
Otsyuda, odnako, otnyud' ne sleduet, chto gravitacionnye volny – vsego lish' igra uma, matematicheskaya abstrakciya. Eto v principe nablyudaemoe fizicheskoe yavlenie. Tak, naprimer, sterzhen', nahodyashiisya v pole gravitacionnoi volny, ispytyvaet deformacii, menyayushiesya s ee chastotoi. Ogovorka "v principe" otnyud' ne sluchaina: massa lyubogo ob'ekta na Zemle nastol'ko mala, a dvizhenie ego stol' medlenno, chto generaciya gravitacionnogo izlucheniya v zemnyh usloviyah sovershenno nichtozhna, ne vidno skol'ko-nibud' real'nogo sposoba zaregistrirovat' takoe izluchenie. Sushestvuet ryad proektov sozdaniya detektorov gravitacionnogo izlucheniya ot kosmicheskih ob'ektov. Odnako i zdes' real'nyh rezul'tatov do sih por net.
Hotya plotnost' energii gravitacionnogo polya v lyuboi tochke mozhno po svoemu zhelaniyu obratit' v nul' vyborom podhodyashei sistemy koordinat, polnaya energiya etogo polya vo vsem ob'eme, polnyi ego impul's imeyut real'nyi fizicheskii smysl (konechno, esli pole dostatochno bystro ubyvaet na beskonechnosti). Stol' zhe nablyudaemoi, horosho opredelennoi velichinoi yavlyaetsya i poterya energii sistemoi za schet gravitacionnogo izlucheniya.
Vse eto imeet pryamoe otnoshenie k pul'saru PSR 1913+16. Eta sistema takzhe dolzhna izluchat' gravitacionnye volny. Ih energiya v dannom sluchae ogromna, ona sravnima s polnoi energiei izlucheniya Solnca. No dazhe etogo nedostatochno, chtoby neposredstvenno zaregistrirovat' eti volny na Zemle. Energiya gravitacionnyh voln mozhet cherpat'sya zdes' tol'ko iz energii orbital'nogo dvizheniya zvezd. Ee umen'shenie privodit k umen'sheniyu rasstoyaniya mezhdu zvezdami. Tshatel'nye izmereniya impul'sov radioizlucheniya ot pul'sara PSR 1913+16 pokazali, chto rasstoyanie mezhdu komponentami etoi dvoinoi zvezdy umen'shaetsya na neskol'ko metrov v god v polnom soglasii s predskazaniem OTO. Poterya energii dvoinoi zvezdoi za schet gravitacionnogo izlucheniya byla vpervye rasschitana sovetskimi fizikami-teoretikami L.D. Landau i E.M. Lifshicem.
6. Gravitacionnye linzy i korichnevye karliki
V 1919 godu A.S. Eddington i O.D. Lodzh nezavisimo zametili, chto, poskol'ku zvezda otklonyaet svetovye luchi, ee mozhno rassmatrivat' kak svoeobraznuyu gravitacionnuyu linzu. Takaya linza smeshaet vidimoe izobrazhenie zvezdy-istochnika otnositel'no ee istinnogo polozheniya.
Pervaya naivnaya ocenka mozhet privesti k vyvodu o polnoi beznadezhnosti nablyudeniya effekta. Iz prostyh soobrazhenii razmernosti mozhno bylo by zaklyuchit', chto izobrazhenie okazhetsya sdvinutym na ugol poryadka rg /d, gde rg – gravitacionnyi radius linzy, a d – harakternoe rasstoyanie v zadache. Dazhe esli vzyat' v kachestve linzy skoplenie, sostoyashee iz 104zvezd, a dlya rasstoyaniya prinyat' ocenku d~10 svetovyh let, to i togda etot ugol sostavil by vsego 10-10 radian. Nablyudenie podobnyh uglov prakticheski nevozmozhno.
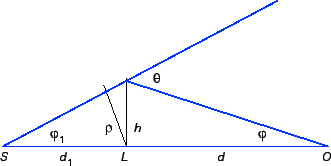
Odnako podobnaya ocenka prosto neverna. Eto sleduet, v chastnosti, iz issledovaniya prosteishego sluchaya soosnogo raspolozheniya istochnika S, linzy L i nablyudatelya O (sm. ris. 2). Zadacha eta byla rassmotrena v 1924 godu O.D. Hvol'sonom i spustya 12 let A. Einshteinom. Obratimsya k nei i my. Yasno, chto dlya vsyakogo rasstoyaniya d1 mezhdu istochnikom i linzoi, d – mezhdu linzoi i nablyudatelem i dlya lyubogo gravitacionnogo radiusa rg linzy (zvezdy ili skopleniya zvezd) naidetsya takoe minimal'noe rasstoyanie ρ mezhdu luchom iz istochnika i linzoi, pri kotorom etot luch popadet v priemnik. Pri etom izobrazheniya istochnika zapolnyayut okruzhnost', kotoruyu nablyudatel' vidit pod uglom φ. Ugly φ i φ1 maly, tak chto φ≈h/d, φ1≈h/d1, a, krome togo, h≈ρ. Otsyuda legko nahodim
| φ=[2rg · ( d1 / [d(d+d1)] ) ]1/2. | (10) |
Takim obrazom, pravil'nyi poryadok velichiny uglovyh razmerov izobrazheniya ne rg /d , a (rg /d)1/2 (zdes' schitaetsya, chto vse rasstoyaniya po poryadku velichiny odinakovy). On okazalsya namnogo bol'she pervoi, naivnoi ocenki, i eto radikal'no menyaet situaciyu s vozmozhnost'yu nablyudeniya effektov gravitacionnyh linz. Izobrazhenie istochnika v vide okruzhnosti (ee prinyato nazyvat' kol'com Einshteina), sozdavaemoe gravitacionnoi linzoi pri aksial'no-simmetrichnom raspolozhenii, real'no nablyudalos'. Seichas izvestno neskol'ko istochnikov v radiodiapazone, kotorye vyglyadyat imenno tak, kol'ceobrazno.
Esli, odnako, gravitacionnaya linza ne lezhit na pryamoi, soedinyayushei istochnik s nablyudatelem, kartina okazyvaetsya inoi. V sluchae sfericheski-simmetrichnoi linzy voznikayut dva izobrazheniya (sm. ris. 3), odno iz kotoryh lezhit vnutri kol'ca Einshteina, sootvetstvuyushego osesimmetrichnoi kartine, a drugoe – snaruzhi. Podobnye izobrazheniya takzhe nablyudalis', oni vyglyadyat kak dvoinye kvazary, kak kvazary-bliznecy.
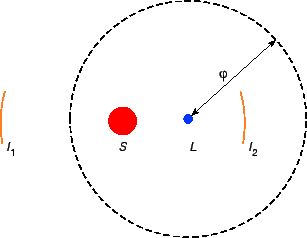 |
Ris. 3. Gravitacionnaya linza. Obshii sluchai. S – proekciya istochnika na frontal'nuyu ploskost', L – proekciya linzy, I1, I2 – izobrazheniya istochnika |
Esli istochnik dvizhetsya, to peremeshayutsya i oba izobrazheniya. Poka yarkosti oboih sravnimy s yarkost'yu istochnika, dlya ocenki uglovogo rasstoyaniya mezhdu nimi mozhno po-prezhnemu ispol'zovat' vyrazhenie (10). Esli massa zvezdy, deistvuyushei v kachestve linzy, nevelika, skazhem, na dva-tri poryadka velichiny men'she massy Solnca, to razreshit' ugol mezhdu izobrazheniyami ~0″,001 prakticheski nemyslimo. Tem ne menee obnaruzhit' podobnoe yavlenie mozhno. Pri sblizhenii izobrazhenii ih summarnaya yarkost' rastet. Yavlenie eto, nazyvaemoe mikrolinzirovaniem, imeet dostatochno specificheskii harakter: rost yarkosti i ee posleduyushee padenie proishodyat simmetrichno vo vremeni, prichem izmenenie yarkosti proishodit odinakovo na vseh dlinah voln (ugol otkloneniya (10) ne zavisit ot dliny volny). Bolee podrobno o gravitacionnom mikrolinzirovanii i kosmicheskih linzah mozhno prochitat' v stat'yah L.M. Eruhimova "Kosmicheskie linzy i ih rol' v issledovanii Vselennoi" i A.M. Cherepashuka "Gravitacionnoe mikrolinzirovanie i problema skrytoi massy" v etom tome.
Poiski yavlenii mikrolinzirovaniya, kotorye velis' na protyazhenii neskol'kih let dvumya gruppami astronomov, avstraliisko-amerikanskoi i francuzskoi, ne prosto priveli k obnaruzheniyu effekta: byl otkryt novyi klass nebesnyh tel – slabosvetyashiesya karlikovye zvezdy, nazyvaemye korichnevymi karlikami. Imenno oni, naryadu s bolee massivnymi belymi karlikami, igrayut rol' mikrolinz. Esli eshe v yanvare 1994 goda bylo izvestno lish' dva-tri podobnyh sobytiya, to v nastoyashee vremya oni uzhe ischislyayutsya desyatkami.
7. Zaklyuchenie
OTO – zavershennaya fizicheskaya teoriya. Ona zavershena v tom zhe smysle, chto i klassicheskaya mehanika, klassicheskaya elektrodinamika, kvantovaya mehanika. Podobno im, ona daet odnoznachnye otvety na fizicheski osmyslennye voprosy, daet chetkie predskazaniya dlya real'no osushestvimyh nablyudenii i eksperimentov. Odnako, kak i vsyakaya inaya fizicheskaya teoriya, OTO imeet svoyu oblast' primenimosti. Tak, vne etoi oblasti lezhat sverhsil'nye gravitacionnye polya, gde vazhny kvantovye effekty. Zakonchennoi kvantovoi teorii gravitacii ne sushestvuet.
OTO – udivitel'naya fizicheskaya teoriya. Ona udivitel'na tem, chto v ee osnove lezhit, po sushestvu, vsego odin eksperimental'nyi fakt, k tomu zhe izvestnyi zadolgo do sozdaniya OTO (vse tela padayut v pole tyazhesti s odinakovym uskoreniem); udivitel'na tem, chto ona sozdana v bol'shoi stepeni odnim chelovekom. No prezhde vsego OTO udivitel'na svoei neobychainoi vnutrennei stroinost'yu, krasotoi. Ne sluchaino L.D. Landau govoril, chto istinnogo fizika-teoretika mozhno raspoznat' po tomu, ispytal li chelovek voshishenie pri pervom zhe znakomstve s OTO.
Primerno do serediny 60-h godov OTO nahodilas' v znachitel'noi mere vne osnovnoi linii razvitiya fiziki. Da i razvitie samoi OTO ne bylo aktivnym, ono svodilos' v bol'shoi stepeni k vyyasneniyu opredelennyh tonkih mest, detalei teorii, k resheniyu pust' vazhnyh, no dostatochno chastnyh zadach. Veroyatno, odna iz prichin takoi situacii sostoit v tom, chto OTO voznikla v nekotorom smysle slishkom rano, Einshtein obognal vremya. S drugoi storony, uzhe v ego rabote 1915 goda teoriya byla sformulirovana v dostatochno zavershennom vide. Ne menee vazhno i to obstoyatel'stvo, chto nablyudatel'naya baza OTO ostavalas' ochen' uzkoi. Sootvetstvuyushie eksperimenty chrezvychaino trudny. Dostatochno napomnit', chto krasnoe smeshenie udalos' izmerit' lish' spustya pochti 40 let posle togo, kak bylo obnaruzheno otklonenie sveta v pole Solnca.
Odnako v nastoyashee vremya OTO – burno razvivayushayasya oblast' sovremennoi fiziki. Eto rezul'tat ogromnogo progressa nablyudatel'noi astronomii, razvitiya eksperimental'noi tehniki, vpechatlyayushego prodvizheniya v teorii.
Literatura
- Gravitaciya bez formul / Per. s angl. M.: Mir, 1985.
- Energetika chernyh dyr. M.: Znanie, 1986.
- Teoriya tyagoteniya Einshteina. Obshie principy i eksperimental'nye sledstviya. M.: MIFI, 1989.
- Prilozheniya teorii tyagoteniya Einshteina k astrofizike i kosmologii. M.: MIFI, 1990.
- Teoriya polya. M.: Nauka, 1988.
- Uspehi fizicheskih nauk. 1999. T. 169. 10. S. 1141.
|
Publikacii s klyuchevymi slovami:
teoriya otnositel'nosti - gravitaciya - princip ekvivalentnosti - gravitacionnye volny - gravitacionnoe linzirovanie
Publikacii so slovami: teoriya otnositel'nosti - gravitaciya - princip ekvivalentnosti - gravitacionnye volny - gravitacionnoe linzirovanie |

|
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |