|
Peremennye Zvezdy (Variable Stars) 44, No. 6, 2024 Received 3 June; accepted 23 September. |
Article in PDF |
|
DOI: 10.24412/2221-0474-2024-44-56-77
|
Catalog of Multi-mode Radially Pulsating Variables: II
A. V. Khruslov1,2
- Sternberg Astronomical Institute, Moscow State University,
Universitetskij pr. 13, Moscow 119992, Russia; khruslov@bk.ru
- Institute of Astronomy, Russian Academy of Sciences, Pyatnitskaya str. 48, Moscow 119017, Russia
|
I present the second part of the catalog of newly
detected Multi-Mode Radially Pulsating (MMRP) variable stars. For
these stars, pulsations in the fundamental, first-, second-, or
third-overtone modes were detected. This paper includes 60 double-
and multi-mode stars (numbered from MMRP-051 to MMRP-110).
Variability types determined for these stars are RR Lyrae
variables and high-amplitude I analyzed all observations available for these stars in the ASAS-SN and ZTF online public archives using the period-search software developed by Dr. V.P. Goranskij for Windows environment. Light elements and parameters of oscillations were determined.
|
1. Introduction
The second part of the catalog of Multi-Mode Radially Pulsating (MMRP) variables is the continuation of my previous paper (Khruslov 2023), the first part of the MMRP catalog, and presents my detection of 60 new double- and multi-mode variables. The star numbers in the second part of the catalog are from MMRP-051 to MMRP-110.
Among these stars, there are RR Lyrae variables and high-amplitude
![]() Scuti (HADS) variables. These are stars that pulsate in
the fundamental mode, the first-, second-, or third-overtone mode.
Scuti (HADS) variables. These are stars that pulsate in
the fundamental mode, the first-, second-, or third-overtone mode.
The method I apply to search for multi-periodicity, the photometric data used, identification names of stars included in the catalog, classification system, and multi-row structure of the tables, with a set of sub-rows, each of them corresponding to a individual detected radial pulsation mode, are the same as those described in the first part of the MMRP catalog.
Searching for double periodicity, I mainly used data available in the photometric archives of the All-Sky Automated Survey for Supernovae (ASAS-SN1, Shappee et al. 2014; Kochanek et al. 2017) and the Zwicky Transient Facility (ZTF, Bellm et al. 2019; Masci et al. 2019). The ZTF data were taken from the SNAD ZTF viewer2, Malanchev et al. (2021). The light elements are based on data from these two surveys. The magnitude ranges and amplitudes of brightness variations are given in the tables according to these data. Additionally, in individual cases, I analyzed available data from other archives: the Wide Angle Search for Planets (SuperWASP3, Butters et al. 2010; 7 variables), the Catalina Sky Surveys (CSS4, Drake et al. 2009; 6 variables). The SuperWASP observations are available as FITS tables, which were converted into ASCII tables using the OMC2ASCII5program as described by Sokolovsky (2007).
In some cases, continuous data series from ZTF, with duration of a whole night of observations, were recalculated as average values that were used for subsequent analysis; they are presented in the data files below the main data series.
The survey data used in this study for the program stars are available online in the html version of this paper as a zip archive. The archive also contains light curves of all variables and a cross-identification table for all stars.
2. Format of presentation
2.1. Identification names
The MMRP catalog uses two types of variable-star identification names:
(1) the format for designating stars whose multiperiodicity was first discovered in this study is:
(2) and the format for designating known multiperiodic stars, for which new light elements are presented, is:
Designations of the type (2) appeared only in the first part of the MMRP.
2.2. Classification
New original MMRP classification of multiperiodic variables is somewhat more detailed than that used in the General Catalog of Variable Stars, GCVS (Samus et al. 2017), but is based on the principles presented by N.N. Samus and the GCVS team at the XXVI IAU General Assembly in Prague, 20066. The studies that have resulted in the MMRP catalog are a part of the program aimed at inclusion of new variables into the GCVS.
The MMRP classification consists of the variability type
designated with a single letter (C - Classical Cepheids; W -
W Virginis type II Cepheids; R - RR Lyrae stars; D -
![]() Scuti stars) and the numerical identification of
pulsation modes (0 - fundamental mode; 1 - first overtone; 2 -
second overtone; 3 - third overtone). Extra characteristics are
introduced with an additional index (n - additional non-radial
mode; m - amplitude modulation with a slow variation from season
to season). An arrow
Scuti stars) and the numerical identification of
pulsation modes (0 - fundamental mode; 1 - first overtone; 2 -
second overtone; 3 - third overtone). Extra characteristics are
introduced with an additional index (n - additional non-radial
mode; m - amplitude modulation with a slow variation from season
to season). An arrow ![]() indicates the cases of mode switching.
Examples: C01, C12m, D0123, D01n, R01, R01
indicates the cases of mode switching.
Examples: C01, C12m, D0123, D01n, R01, R01![]() R0.
R0.
The radial pulsation modes were identified on the base of the
period ratio (
![]() ); see the study of this
problem in Petersen (1973), Petersen & Christensen-Dalsgaard
(1996), Smolec & Moskalik (2010), etc.
); see the study of this
problem in Petersen (1973), Petersen & Christensen-Dalsgaard
(1996), Smolec & Moskalik (2010), etc.
2.3. Tables
We use a multi-row format in the Tables of the MMRP catalog. For a complete description of the format, see the first part of the MMRP catalog (Khruslov 2023).
The main table (Table 1) contains general information on the star:
number in the MMRP Catalog; equatorial coordinates J2000;
magnitude range; type of multi-periodicity; and then, information
about individual modes is presented in sub-rows (light elements,
period and epoch of maximum; semi-amplitude; asymmetry parameter
of the phased light curve, ![]() -
-![]() ). The period ratio
). The period ratio ![]() (shorter period / longer period) is given for each pair of
adjacent sub-rows (in the sub-row for the longer period).
(shorter period / longer period) is given for each pair of
adjacent sub-rows (in the sub-row for the longer period).
The equatorial coordinates are given according to the Gaia DR3
catalog. The tabulated magnitude range is for the photometric band
indicated in brackets (a![]() and a
and a![]() are ASAS-SN
are ASAS-SN ![]() and
and ![]() magnitudes; z
magnitudes; z![]() and z
and z![]() are ZTF
are ZTF ![]() and
and ![]() magnitudes).
Semi-amplitudes are given in the photometric band indicated in the
“Magn.” column.
magnitudes).
Semi-amplitudes are given in the photometric band indicated in the
“Magn.” column.
In addition to the notation used in the MMRP-I catalog, the second part (this paper) contains epochs in the following three formats:
![]() ;
;
![]() ;
;
![]() .
.
In the second part of the MMRP, I do not present separate tables of comments in the format of coded numbers (Tables 2 and 2a in MMRP-I). After Table 1, I present comments for individual stars. I excluded information about the history of variability studies for individual stars that was included in the Comments of the first MMRP catalog. This information can be found in the web sources of the photometric surveys: the ASAS-SN catalogs of variable stars7(Jayasinghe et al. 2018, 2019a, 2019b, 2020, 2021); the ZTF catalog of periodic variable stars8, Chen et al. (2020); Gaia DR2 and Gaia DR3, and others. Identifications with these catalogs can be found in the cross-identification table available online in the html version of this paper (see the link in Section 1).
The supplementary Tables 2 and 3 (corresponding respectively to Tables 3 and 4 in MMRP-I) contain semi-amplitudes and magnitude ranges in all bands used in the ASAS-SN and ZTF surveys and known information from catalogs and photometric surveys: color indices and Galactic latitudes.
2.4. Light curves
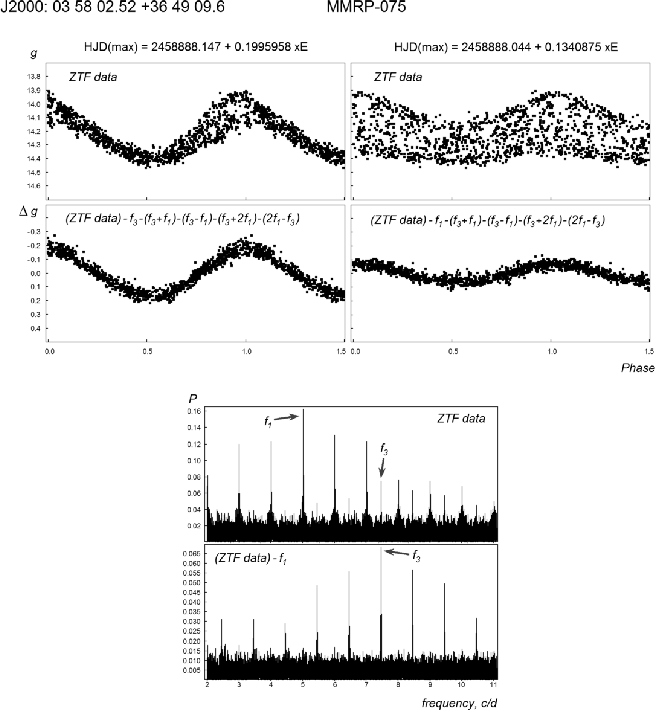
An example of light curves for one of the stars, MMRP-075, is
displayed in Fig. 1. The star is classified as a D13 type
variable. The top panels present data folded with the first- and
third-overtone periods. The bottom panels show the same curves
after prewhitening the other oscillation (also, the ![]() ,
,
![]() ,
, ![]() , and
, and ![]() interaction
frequencies were excluded). Along with the light curves, we
present power spectra of the double-mode variables, for the raw
data and after subtraction of the dominant mode (the
first-overtone oscillation in the case of MMRP-075). The
structure of the power spectra shows that the secondary periods
are real.
interaction
frequencies were excluded). Along with the light curves, we
present power spectra of the double-mode variables, for the raw
data and after subtraction of the dominant mode (the
first-overtone oscillation in the case of MMRP-075). The
structure of the power spectra shows that the secondary periods
are real.
The light curves for all studied stars are available online in the html version of this paper as a zip archive (see the link in Section 1). The light curves are given in the format displayed in Fig. 1. A similar and more complete format is used for triple- and quadruple-mode variables.
3. Results
Among the 60 stars presented in this paper, there are 10 RR Lyrae
stars of the R01 type, 50 high-amplitude ![]() Scuti stars
(double-mode: 22 stars of the D01 type; 8 D12 stars; 3 D02 stars;
10 D13 stars; triple-mode: one D012 star and 5 D123 stars; one
quadruple-mode D0123 star). Stars of the D02 and D13 types have
not been studied by me before. Double-mode or multi-mode Cepheids
are not presented in this paper.
Scuti stars
(double-mode: 22 stars of the D01 type; 8 D12 stars; 3 D02 stars;
10 D13 stars; triple-mode: one D012 star and 5 D123 stars; one
quadruple-mode D0123 star). Stars of the D02 and D13 types have
not been studied by me before. Double-mode or multi-mode Cepheids
are not presented in this paper.
In addition, one of the previously studied stars, MMRP-010, was reclassified as a D01 star.
| No. | J2000 | Magn. | Type | Period, d | Epoch | Ampl. |
|
|
| 010 | 04 53 16.75 | 14.37 - | D01 | 0.323070 | b0.036 | 0.164 | 0.37 | 0.7547 |
| +39 14 18.2 | 15.21 (a |
0.243812 | b0.100 | 0.136 | 0.55 | |||
| 051 | 00 06 39.46 | 17.67 - | D13 | 0.0675897 | b0.0012 | 0.210 | 0.38 | 0.6749 |
| +53 13 44.0 | 18.24 (z |
0.0456185 | b0.0414 | 0.018 | 0.50 | |||
| 052 | 00 09 33.51 | 17.84 - | D01 | 0.0836583 | b0.0165 | 0.139 | 0.39 | 0.7749 |
| +56 21 44.4 | 18.43 (z |
0.0648244 | b0.0040 | 0.054 | 0.44 | |||
| 053 | 00 10 52.50 | 17.63 - | D01 | 0.1539483 | b0.0427 | 0.140 | 0.38 | 0.7688 |
| +56 31 18.5 | 18.50 (z |
0.1183604 | b0.0285 | 0.162 | 0.35 | |||
| 054 | 00 14 24.72 | 16.05 - | D01 | 0.0859502 | b0.0654 | 0.183 | 0.36 | 0.7742 |
| +53 20 52.7 | 16.50 (z |
0.0665394 | b0.0105 | 0.017 | 0.50 | |||
| 055 | 00 23 45.18 | 17.33 - | D01 | 0.1097914 | b0.1045 | 0.060 | 0.40 | 0.7735 |
| +64 45 54.9 | 17.83 (z |
0.0849198 | b0.0690 | 0.112 | 0.40 | |||
| 056 | 00 27 07.81 | 15.47 - | D012 | 0.1165398 | b0.0500 | 0.035 | 0.47 | 0.7703 |
| +57 37 40.7 | 15.90 (z |
0.0897679 | b0.0499 | 0.140 | 0.39 | 0.8015 | ||
| 0.0719476 | b0.0645 | 0.016 | 0.50 | |||||
| 057 | 00 29 28.85 | 17.18 - | D01 | 0.06204725 | b0.0154 | 0.170 | 0.38 | 0.7766 |
| +54 18 42.6 | 17.69 (z |
0.0481865 | b0.0170 | 0.031 | 0.48 | |||
| 058 | 00 29 30.75 | 15.91 - | R01 | 0.465953 | b0.067 | 0.132 | 0.40 | 0.7434 |
| +50 45 40.7 | 16.60 (z |
0.346377 | b0.097 | 0.159 | 0.39 | |||
| 059 | 00 35 42.60 | 17.76 - | D01 | 0.1457098 | b0.127 | 0.053 | 0.42 | 0.7709 |
| +64 27 12.6 | 18.08 (z |
0.1123257 | b0.043 | 0.042 | 0.39 | |||
| 060 | 00 37 28.27 | 17.77 - | D01 | 0.0766737 | b0.0408 | 0.245 | 0.34 | 0.7500 |
| +55 20 00.3 | 18.52 (z |
0.0575075 | b0.0340 | 0.029 | 0.46 | |||
| 061 | 00 45 27.68 | 16.31 - | D01 | 0.0946369 | b0.0235 | 0.154 | 0.37 | 0.7719 |
| +58 53 58.9 | 17.20 (z |
0.0730509 | b0.0304 | 0.146 | 0.35 | |||
| 062 | 00 48 11.14 | 13.58 - | D13 | 0.0793879 | b0.0215 | 0.245 | 0.37 | 0.6714 |
| +47 37 19.0 | 14.25 (a |
0.0533018 | b0.0097 | 0.025 | 0.50: | |||
| 063 | 00 50 42.33 | 17.79 - | D13 | 0.0845786 | b0.0470 | 0.175 | 0.40 | 0.6514 |
| +56 51 08.9 | 18.30 (z |
0.0550910 | b0.0260 | 0.018 | 0.50 | |||
| 064 | 00 51 37.66 | 17.35 - | D12 | 0.0930969 | b0.0701 | 0.211 | 0.40 | 0.8035 |
| +68 45 17.0 | 17.95 (z |
0.0748047 | b0.0738 | 0.023 | 0.43: | |||
| 065 | 00 51 41.52 | 16.88 - | D01 | 0.0853045 | b0.0130 | 0.174 | 0.36 | 0.7744 |
| +52 43 16.3 | 17.55 (z |
0.0660640 | b0.0406 | 0.082 | 0.41 | |||
| 066 | 01 00 46.09 | 18.13 - | D01 | 0.0653560 | b0.0567 | 0.120 | 0.37 | 0.7525 |
| +71 59 36.6 | 18.54 (z |
0.0491802 | b0.0315 | 0.016 | 0.44 | |||
| 067 | 02 37 13.67 | 15.38 - | D12 | 0.0985287 | b0.0244 | 0.140 | 0.38 | 0.8035 |
| +63 02 49.9 | 15.75 (z |
0.0791710 | b0.0138 | 0.010 | 0.50 | |||
| 068 | 02 43 26.13 | 18.00 - | D12 | 0.0821909 | b0.0283 | 0.214 | 0.35 | 0.8027 |
| +65 21 01.1 | 18.63 (z |
0.0659757 | b0.0205 | 0.015 | 0.50 | |||
| 069 | 02 46 59.99 | 17.34 - | D13m | 0.0841481 | b0.0759 | 0.221 | 0.38 | 0.6736 |
| +61 35 38.7 | 17.95 (z |
0.0566862 | b0.0105 | 0.042 | 0.48 | |||
| 070 | 03 20 12.89 | 16.62 - | D13 | 0.0662601 | b0.0240 | 0.070 | 0.43 | 0.6581 |
| +62 34 13.0 | 16.84 (z |
0.0436084 | b0.0097 | 0.015 | 0.47 | |||
| 071 | 03 23 43.84 | 18.10 - | D01 | 0.1094991 | b0.0757 | 0.059 | 0.47 | 0.7730 |
| +62 52 47.9 | 18.45 (z |
0.0846419 | b0.0545 | 0.053 | 0.48 | |||
| 072 | 03 34 42.83 | 17.43 - | D01 | 0.1028625 | b0.0866 | 0.099 | 0.39 | 0.7715 |
| +60 31 08.3 | 17.77 (z |
0.0793606 | b0.0250 | 0.026 | 0.46 | |||
| 073 | 03 43 18.44 | 16.34 - | D13 | 0.0911844 | b0.0530 | 0.065 | 0.45 | 0.6484 |
| +68 31 57.1 | 16.56 (z |
0.0591228 | b0.0183 | 0.019 | 0.47 | |||
| 074 | 03 52 55.98 | 18.09 - | D01 | 0.1074287 | b0.0740 | 0.152 | 0.35 | 0.7730 |
| +55 03 33.5 | 18.63 (z |
0.0830433 | b0.0470 | 0.054 | 0.39 | |||
| 075 | 03 58 02.52 | 13.92 - | D13 | 0.1995958 | b0.147 | 0.168 | 0.48 | 0.6718 |
| +36 49 09.6 | 14.45 (z |
0.1340875 | b0.044 | 0.061 | 0.45 | |||
| 076 | 04 05 46.65 | 16.45 - | D12 | 0.1301875 | b0.0945 | 0.167 | 0.43 | 0.8038 |
| +57 40 21.6 | 16.90 (z |
0.104641 | b0.0592 | 0.023 | 0.46 | |||
| 077 | 04 09 46.34 | 17.02 - | D12 | 0.0740534 | b0.0345 | 0.119 | 0.37 | 0.8073 |
| +53 07 47.6 | 17.37 (z |
0.0597822 | b0.0587 | 0.012 | 0.44 | |||
| 078 | 04 18 00.38 | 16.27 - | D0123 | 0.1224802 | b0.0825 | 0.051 | 0.42 | 0.7722 |
| +56 08 42.3 | 16.60 (z |
0.0945762 | b0.0225 | 0.057 | 0.42 | 0.8048 | ||
| 0.0761115 | b0.0693 | 0.023 | 0.47 | 0.8336 | ||||
| 0.0634467 | b0.0250 | 0.029 | 0.50 | |||||
| 079 | 04 19 16.52 | 17.41 - | D01 | 0.0838792 | b0.0404 | 0.137 | 0.31 | 0.7747 |
| +57 14 23.1 | 17.83 (z |
0.0649833 | b0.0145 | 0.018 | 0.48 | |||
| 080 | 05 15 27.80 | 16.59 - | D01 | 0.0701374 | b0.0374 | 0.234 | 0.32 | 0.7763 |
| +70 36 58.8 | 17.42 (z |
0.0544502 | b0.0325 | 0.058 | 0.46 | |||
| 081 | 05 28 53.05 | 13.20 - | D123 | 0.1482472 | b0.144 | 0.076 | 0.43 | 0.8018 |
| +48 36 11.8 | 13.41 (z |
0.1188605 | b0.105 | 0.009 | 0.50 | 0.8322 | ||
| 0.0989185 | b0.019 | 0.013 | 0.48 | |||||
| 082 | 07 14 14.39 | 13.72 - | D12m | 0.0915925 | b0.0885 | 0.224 | 0.35 | 0.8055 |
| +73 27 29.6 | 14.33 (z |
0.0737798 | b0.0296 | 0.035 | 0.50 | |||
| 083 | 09 48 09.85 | 13.36 - | D13n | 0.08640150 | b0.0125 | 0.101 | 0.44 | 0.6601 |
| -61 19 30.3 | 13.69 (a |
0.05703713 | b0.0540 | 0.011 | 0.53: | |||
| 084 | 14 01 22.52 | 18.60 - | R01 | 0.542780 | b0.245 | 0.058 | 0.50: | 0.7467 |
| +26 39 00.5 | 19.40 (z |
0.405293 | b0.212 | 0.224 | 0.39 | |||
| 085 | 14 03 54.78 | 16.74 - | R01 | 0.489193 | b0.160 | 0.194 | 0.41 | 0.7437 |
| +67 08 42.6 | 17.73 (z |
0.363813 | b0.072 | 0.235 | 0.39 | |||
| 086 | 14 31 33.52 | 12.80 - | D02n: | 0.09348775 | b0.0181 | 0.135 | 0.41 | 0.6102 |
| -44 14 40.3 | 13.18 (a |
0.05704222 | b0.0082 | 0.013 | 0.48 | |||
| 087 | 14 50 44.40 | 14.29 - | D02 | 0.1817898 | b0.071 | 0.235 | 0.32 | 0.5987 |
| -51 09 56.0 | 15.01 (a |
0.1088370 | b0.044 | 0.025 | 0.43 | |||
| 088 | 15 03 57.99 | 19.32 - | R01 | 0.58066 | b0.398 | 0.057 | 0.40 | 0.7462 |
| +67 12 16.7 | 20.15 (z |
0.43331 | b0.187 | 0.216 | 0.35 | |||
| 089 | 15 19 31.77 | 13.61 - | D123 | 0.1691712 | b0.068 | 0.102 | 0.47 | 0.7994 |
| -62 58 21.0 | 14.10 (a |
0.1352296 | b0.055 | 0.037 | 0.49 | 0.8316 | ||
| 0.1124590 | b0.073 | 0.040 | 0.46 | |||||
| 090 | 15 46 05.81 | 16.99 - | R01 | 0.473777 | b0.362 | 0.182 | 0.41 | 0.7440 |
| +79 22 24.7 | 18.01 (z |
0.352505 | b0.016 | 0.220 | 0.37 | |||
| 091 | 15 56 32.39 | 13.90 - | D01m | 0.0707824 | a0.0124 | 0.141 | 0.38 | 0.7702 |
| -38 48 02.0 | 14.55 (a |
0.0545141 | a0.0330 | 0.071 | 0.50: | |||
| 092 | 16 07 49.75 | 17.29 - | R01 | 0.486850 | b0.070 | 0.033 | 0.47 | 0.7445 |
| +20 16 56.9 | 17.89 (z |
0.362469 | b0.170 | 0.231 | 0.40 | |||
| 093 | 16 26 25.26 | 16.86 - | R01 | 0.481098 | b0.183 | 0.151 | 0.40 | 0.7444 |
| +69 44 18.3 | 17.80 (a |
0.358113 | b0.007 | 0.222 | 0.38 | |||
| 094 | 16 29 16.93 | 13.14 - | D02 | 0.16514947 | b0.0733 | 0.177 | 0.34 | 0.6089 |
| -20 49 49.2 | 13.61 (a |
0.1005594 | b0.0828 | 0.020 | 0.48 | |||
| 095 | 16 49 42.63 | 17.11 - | R01 | 0.475254 | b0.060 | 0.169 | 0.40 | 0.7444 |
| +47 53 42.6 | 18.11 (z |
0.353766 | b0.324 | 0.226 | 0.38 | |||
| 096 | 17 50 31.00 | 11.76 - | D13 | 0.1239932 | b0.1177 | 0.075 | 0.46 | 0.6593 |
| -28 11 35.6 | 12.00 (a |
0.0817480 | b0.0522 | 0.015 | 0.45 | |||
| 097 | 18 00 55.06 | 14.48 - | D01 | 0.1176389 | b0.021 | 0.235 | 0.36 | 0.7717 |
| -56 45 32.7 | 15.40 (a |
0.0907838 | b0.063 | 0.063 | 0.43 | |||
| 098 | 18 01 23.93 | 18.70 - | R01 | 0.547167 | b0.435 | 0.097 | 0.43 | 0.7460 |
| +46 12 26.2 | 19.62 (z |
0.408183 | b0.153 | 0.234 | 0.37 | |||
| 099 | 18 13 15.97 | 14.47 - | D123 | 0.1163633 | b0.0233 | 0.060 | 0.50 | 0.7996 |
| -16 04 22.1 | 14.72 (z |
0.0930402 | b0.0685 | 0.023 | 0.49 | 0.8297 | ||
| 0.0771944 | b0.0418 | 0.020 | 0.43 | |||||
| 100 | 18 32 35.84 | 12.38 - | D123n | 0.1763344 | b0.081 | 0.099 | 0.46 | 0.7980 |
| +23 45 13.1 | 12.83 (a |
0.1407097 | b0.065 | 0.028 | 0.49 | 0.8225 | ||
| 0.1157337 | b0.020 | 0.043 | 0.49 | |||||
| 101 | 18 41 51.71 | 19.2 - | R01 | 0.513113 | b0.135 | 0.045 | 0.47 | 0.7458 |
| +19 34 59.4 | 19.7 (z |
0.382661 | b0.382 | 0.143 | 0.43 | |||
| 102 | 18 57 09.54 | 15.10 - | D01 | 0.08030705 | b0.0360 | 0.065 | 0.44 | 0.7755 |
| -29 32 13.2 | 15.60 (a |
0.06228179 | b0.0437 | 0.062 | 0.43 | |||
| 103 | 19 11 49.38 | 13.60 - | D01 | 0.07061797 | b0.0125 | 0.152 | 0.38 | 0.7738 |
| -27 44 44.1 | 14.16 (a |
0.05464646 | b0.0336 | 0.051 | 0.45 | |||
| 104 | 19 45 52.97 | 17.58 - | D01n | 0.0815354 | b0.0316 | 0.108 | 0.41 | 0.7849 |
| +16 41 58.7 | 18.25 (z |
0.0640002 | b0.0307 | 0.110 | 0.37 | |||
| 105 | 19 45 53.19 | 14.41 - | D123 | 0.1565323 | b0.0925 | 0.174 | 0.39 | 0.7969 |
| +19 17 04.3 | 14.87 (z |
0.1247345 | b0.0870 | 0.018 | 0.50: | 0.8332 | ||
| 0.1039327 | b0.0077 | 0.010 | 0.44: | |||||
| 106 | 19 48 42.16 | 15.67 - | D12 | 0.1284792 | b0.0088 | 0.128 | 0.44 | 0.7982 |
| +18 20 51.4 | 16.03 (z |
0.1025547 | b0.0339 | 0.013 | 0.45 | |||
| 107 | 19 56 54.19 | 13.92 - | D13n | 0.07672450 | b0.0440 | 0.093 | 0.45 | 0.6715 |
| -22 53 31.5 | 14.24 (a |
0.05151785 | b0.0498 | 0.019 | 0.50 | |||
| 108 | 20 36 21.97 | 15.15 - | D01 | 0.0644808 | b0.0219 | 0.110 | 0.47 | 0.7792 |
| -50 02 15.3 | 15.80 (a |
0.0502418 | b0.0085 | 0.115 | 0.44 | |||
| 109 | 23 46 17.96 | 17.54 - | D01m | 0.0911045 | b0.0065 | 0.104 | 0.44 | 0.7772 |
| +53 34 08.9 | 18.12 (z |
0.0708039 | b0.0327 | 0.091 | 0.43 | |||
| 110 | 23 46 29.54 | 16.84 - | D12 | 0.0892052 | b0.0878 | 0.259 | 0.38 | 0.8034 |
| +64 10 27.3 | 17.52 (z |
0.0716654 | b0.0567 | 0.024 | 0.48 | |||
Comments to Table 1.
MMRP-054. A blend in the ASAS-SN data is possible, amplitude underestimated. Due to large errors, this data is not included in the table.
MMRP-062. The third-overtone period ![]() varies. The elements in
the Table are given for the
varies. The elements in
the Table are given for the ![]() ASAS-SN and
ASAS-SN and ![]() and
and ![]() ZTF data
time interval. The elements for the
ZTF data
time interval. The elements for the ![]() -band ASAS-SN time
interval are:
-band ASAS-SN time
interval are:
![]() HJD(max) = 2457777.0115 + 0
HJD(max) = 2457777.0115 + 0![]() 0533036
0533036 ![]() .
.
The first-overtone period ![]() also possibly varies.
also possibly varies.
MMRP-064. Amplitude modulation with slow variation from one
season to another is possible for the second-overtone oscillation
![]() . Type D12m is not excluded.
. Type D12m is not excluded.
MMRP-067. A blend in the ASAS-SN data is possible, amplitude underestimated.
MMRP-069. The period ![]() varies. Elements for
varies. Elements for ![]() are given
for the whole time interval covered with observations. The Table
gives light elements for the first time interval in ZTF data, JD
2458287-2459150. The light elements for the second time interval
in ZTF data, JD 2459150-2459995, are:
are given
for the whole time interval covered with observations. The Table
gives light elements for the first time interval in ZTF data, JD
2458287-2459150. The light elements for the second time interval
in ZTF data, JD 2459150-2459995, are:
![]()
![]() : HJD(max) = 2459600.0530 + 0
: HJD(max) = 2459600.0530 + 0![]() 0841481
0841481
![]() ;
;
![]()
![]() : HJD(max) = 2459600.0160 + 0
: HJD(max) = 2459600.0160 + 0![]() 0566891
0566891
![]() ;
;
![]() = 0.155 and
= 0.155 and ![]() = 0.014 in the z
= 0.014 in the z![]() band,
band,
![]() = 0.219 and
= 0.219 and ![]() = 0.021 in the z
= 0.021 in the z![]() band.
band.
MMRP-075. Data from 1SWASP and CSS were used to improve the light
elements. Magnitude range and semi-amplitude according to 1SWASP
data: 14![]() 32-15
32-15![]() 34 (1SWASP mag);
34 (1SWASP mag); ![]() = 0.234,
= 0.234, ![]() =
0.097. According to CSS data: 13
=
0.097. According to CSS data: 13![]() 15-13
15-13![]() 56 (C
56 (C![]() );
); ![]() =
0.123,
=
0.123, ![]() = 0.046. In the 1SWASP data, the oscillation
amplitude is the largest.
= 0.046. In the 1SWASP data, the oscillation
amplitude is the largest.
MMRP-076. A blend in ASAS-SN data is possible, amplitude underestimated.
MMRP-078. Other period ratios: ![]() = 0.6214,
= 0.6214, ![]() =
0.6709.
=
0.6709.
MMRP-081. The first overtone period ![]() possibly varies. In the
ASAS-SN
possibly varies. In the
ASAS-SN ![]() -band data (earlier time interval), the
second-overtone oscillation
-band data (earlier time interval), the
second-overtone oscillation ![]() is not detected, amplitude of
the third-overtone mode
is not detected, amplitude of
the third-overtone mode ![]() is the largest. Amplitude modulation
is not excluded.
is the largest. Amplitude modulation
is not excluded.
MMRP-082. Amplitude modulation of the second overtone oscillation. The photometry was studied in three time intervals:
I. JD 2455970-2458452. Only a![]() data. The first overtone
elements are:
data. The first overtone
elements are:
![]()
![]() : HJD(max) = 2457777.0710 + 0
: HJD(max) = 2457777.0710 + 0![]() 0915920
0915920
![]() ;
; ![]() -
-![]() = 0.35.
= 0.35.
The semi-amplitude is ![]() = 0.190 (a
= 0.190 (a![]() ).
).
The detection of the second-overtone mode ![]() is very uncertain,
the possible period
is very uncertain,
the possible period ![]() = 0
= 0![]() 737833,
737833,
![]() .
.
II. JD 2458034-2458994. The analysis made use of the a![]() , z
, z![]() ,
and z
,
and z![]() data. The light elements and amplitudes for this time
interval are presented in the Tables.
data. The light elements and amplitudes for this time
interval are presented in the Tables.
III. JD 2459076-2460373. The light elements are the following:
![]()
![]() : HJD(max) = 2460000.0290 + 0
: HJD(max) = 2460000.0290 + 0![]() 0915930
0915930
![]() ;
; ![]() -
-![]() = 0.37;
= 0.37;
The semi-amplitudes are: ![]() (a
(a![]() ), 0.160 (z
), 0.160 (z![]() ), 0.240
(z
), 0.240
(z![]() ).
).
![]()
![]() : HJD(max) = 2460000.0360 + 0
: HJD(max) = 2460000.0360 + 0![]() 07378
07378
![]() ;
; ![]() -
-![]() = 0.50:.
= 0.50:.
The semi-amplitudes are: ![]() (a
(a![]() ), 0.006
(z
), 0.006
(z![]() ), 0.007 (z
), 0.007 (z![]() ).
).
MMRP-083. There is an additional non-radial pulsation ![]() with
the following light elements:
with
the following light elements:
![]() HJD(max) = 2458888.0432 + 0
HJD(max) = 2458888.0432 + 0![]() 05668265
05668265 ![]() ;
;
The semi-amplitudes ![]() are 0.009 (a
are 0.009 (a![]() ), 0.008
(a
), 0.008
(a![]() ).
). ![]() -
-![]() = 0.49.
= 0.49.
MMRP-085. Amplitudes and magnitude range in the ![]() -band of ZTF
data:
-band of ZTF
data: ![]() = 0.102,
= 0.102, ![]() = 0.113; 16
= 0.113; 16![]() 89-17
89-17![]() 44.
44.
MMRP-086. Data from 1SWASP were used to improve the light
elements. Magnitude range and semi-amplitudes according to 1SWASP
data: ![]() = 0.078,
= 0.078, ![]() = 0.013; 12
= 0.013; 12![]() 59-12
59-12![]() 85 (1SWASP
mag).
85 (1SWASP
mag).
An additional, possibly non-radial, pulsation ![]() was found with
certainty in the
was found with
certainty in the ![]() -band ASAS-SN data; in the
-band ASAS-SN data; in the ![]() -band ASAS-SN
and 1SWASP data, it is uncertain. Its light elements are the
following:
-band ASAS-SN
and 1SWASP data, it is uncertain. Its light elements are the
following:
![]() HJD(max) = 2458888.0410 + 0
HJD(max) = 2458888.0410 + 0![]() 07345498
07345498 ![]() .
.
The semi-amplitudes ![]() are 0.007: (a
are 0.007: (a![]() ), 0.008
(a
), 0.008
(a![]() ), 0.003: (1SWASP mag). The period ratio
), 0.003: (1SWASP mag). The period ratio ![]() = 0.7857
possibly corresponds to the
= 0.7857
possibly corresponds to the ![]() ratio, but
ratio, but ![]() =
0.7766 does not correspond to the
=
0.7766 does not correspond to the ![]() ratio.
ratio.
MMRP-088. The amplitudes and magnitude range in the ![]() band of
ZTF data:
band of
ZTF data: ![]() ,
, ![]() ; 19
; 19![]() 26-19
26-19![]() 83.
83.
MMRP-090. The amplitude and magnitude range in the ![]() band of
ZTF data:
band of
ZTF data: ![]() ,
, ![]() ; 17
; 17![]() 12-17
12-17![]() 71.
71.
MMRP-091. Type D01![]() D0 is not excluded. ASAS-SN data were
analyzed in four separate time intervals:
D0 is not excluded. ASAS-SN data were
analyzed in four separate time intervals:
![]() I, JD 2457400-2458100,
I, JD 2457400-2458100, ![]() band;
band;
![]() II, JD 2458100-2458800,
II, JD 2458100-2458800, ![]() and
and ![]() bands;
bands;
![]() III, JD 2458800-2459500,
III, JD 2458800-2459500, ![]() band;
band;
![]() IV, JD 2459600-2460400,
IV, JD 2459600-2460400, ![]() band.
band.
In the data for time interval I, double periodicity was detected,
the light elements are given in the Table. In the data for time
interval II, the first-overtone oscillation in the ![]() -band data
was possibly detected (very uncertainly) with a small amplitude
and a different period. The possible period
-band data
was possibly detected (very uncertainly) with a small amplitude
and a different period. The possible period
![]() :,
:, ![]() = 0.014 (a
= 0.014 (a![]() ). In
). In ![]() -band data for the
time interval II,
-band data for the
time interval II, ![]() was not detected. In the data for the time
intervals III and IV,
was not detected. In the data for the time
intervals III and IV, ![]() was not detected.
was not detected.
The fundamental-mode period ![]() varies, the following light
elements were derived for separate time intervals:
varies, the following light
elements were derived for separate time intervals:
![]() II: HJD(max) = 2458500.0423 + 0
II: HJD(max) = 2458500.0423 + 0![]() 0707801
0707801
![]() ;
; ![]() = 0.201 (a
= 0.201 (a![]() ), 0.167 (a
), 0.167 (a![]() );
);
![]() III: HJD(max) = 2459200.0544 + 0
III: HJD(max) = 2459200.0544 + 0![]() 0707797
0707797
![]() ;
; ![]() = 0.201 (a
= 0.201 (a![]() );
);
![]() IV: HJD(max) = 2460000.0212 + 0
IV: HJD(max) = 2460000.0212 + 0![]() 0707817
0707817
![]() ;
; ![]() = 0.199 (a
= 0.199 (a![]() ).
).
In the earlier time interval of 1SWASP data, JD 2453860-2454275, double-mode periodicity was detected with the following elements:
![]()
![]() : HJD(max) = 2454054.0025 + 0
: HJD(max) = 2454054.0025 + 0![]() 0707800
0707800
![]() ;
; ![]() -
-![]() = 0.40,
= 0.40,
![]()
![]() : HJD(max) = 2454054.0025 + 0
: HJD(max) = 2454054.0025 + 0![]() 0545125
0545125
![]() ;
; ![]() -
-![]() = 0.45.
= 0.45.
The semi-amplitudes are ![]() = 0.186,
= 0.186, ![]() = 0.055 (1SWASP
mag).
= 0.055 (1SWASP
mag).
In the 1SWASP data, after removing the radial frequencies ![]() and
and ![]() as well as interaction frequencies (
as well as interaction frequencies (![]() and
and
![]() ), a possible non-radial oscillation
), a possible non-radial oscillation ![]() with the
period
with the
period
![]() is detected,
is detected, ![]() = 0.018 (1SWASP
mag). In the
= 0.018 (1SWASP
mag). In the ![]() -band ASAS-SN data for all time intervals (I and
II), this frequency is not detected. In the
-band ASAS-SN data for all time intervals (I and
II), this frequency is not detected. In the ![]() -band ASAS-SN data
for all time intervals (II, III and IV), this oscillation is
detected:
-band ASAS-SN data
for all time intervals (II, III and IV), this oscillation is
detected:
![]() II:
II:
![]() :,
:, ![]() = 0.015;
= 0.015;
![]() III:
III:
![]() ,
, ![]() = 0.020;
= 0.020;
![]() IV:
IV:
![]() ,
, ![]() = 0.012.
= 0.012.
MMRP-092. The magnitude range according to CSS data:
17![]() 06-17
06-17![]() 61 (C
61 (C![]() ). In CSS data,
). In CSS data, ![]() is not detected.
is not detected.
MMRP-093. The amplitudes and magnitude range in the ![]() band of
ZTF data:
band of
ZTF data: ![]() = 0.081,
= 0.081, ![]() = 0.115; 17
= 0.115; 17![]() 04-17
04-17![]() 52.
52.
MMRP-094. Data from 1SWASP were used to improve the light
elements. The amplitudes and magnitude range in the 1SWASP data:
![]() = 0.146,
= 0.146, ![]() = 0.016; 13
= 0.016; 13![]() 08-13
08-13![]() 54 (1SWASP mag).
54 (1SWASP mag).
MMRP-095. The amplitudes and magnitude range in the ![]() band of
ZTF data:
band of
ZTF data: ![]() = 0.091,
= 0.091, ![]() = 0.119; 17
= 0.119; 17![]() 31-17
31-17![]() 82. The
amplitudes and magnitude range according to CSS data:
82. The
amplitudes and magnitude range according to CSS data: ![]() =
0.099,
=
0.099, ![]() = 0.137; 17
= 0.137; 17![]() 04-17
04-17![]() 93 (C
93 (C![]() ). Data from CSS
were used to improve the light elements.
). Data from CSS
were used to improve the light elements.
MMRP-098. The amplitudes and magnitude range in the ![]() band of
ZTF data:
band of
ZTF data: ![]() = 0.054,
= 0.054, ![]() = 0.130; 18
= 0.130; 18![]() 79-19
79-19![]() 34. In CSS
data, the fundamental mode period
34. In CSS
data, the fundamental mode period ![]() is not detected, magnitude
range 18
is not detected, magnitude
range 18![]() 7-19
7-19![]() 6 (C
6 (C![]() ).
).
MMRP-099. In ASAS-SN ![]() -band data, the second-overtone
frequency
-band data, the second-overtone
frequency ![]() is not detected. Amplitude modulation is not
excluded.
is not detected. Amplitude modulation is not
excluded.
MMRP-100. An additional non-radial pulsation with the period
![]() , or Blazhko effect of the second-overtone
oscillation with
, or Blazhko effect of the second-overtone
oscillation with
![]() . Semi-amplitude
. Semi-amplitude ![]() is 0.022
(a
is 0.022
(a![]() ), 0.023 (a
), 0.023 (a![]() ).
).
Data from 1SWASP were used to improve the light elements. The
semi-amplitudes are ![]() ,
, ![]() ,
, ![]() ,
,
![]() . Blend in 1SWASP data.
. Blend in 1SWASP data.
MMRP-103. According to 1SWASP data, the light elements are:
![]()
![]() : HJD(max) = 2454150.0410 + 0
: HJD(max) = 2454150.0410 + 0![]() 0706180
0706180
![]() ;
;
![]()
![]() : HJD(max) = 2454150.0124 + 0
: HJD(max) = 2454150.0124 + 0![]() 0546466
0546466
![]() .
.
The magnitude range and semi-amplitudes according to 1SWASP data:
13![]() 75-14
75-14![]() 15,
15, ![]() ,
, ![]() .
.
MMRP-104. A possible non-radial oscillation with the period
![]() ; the semi-amplitude
; the semi-amplitude ![]() is 0.021 (z
is 0.021 (z![]() ), 0.016
(z
), 0.016
(z![]() ).
).
![]() , identification with the second
overtone is not excluded.
, identification with the second
overtone is not excluded.
MMRP-105. A blend in ASAS-SN data, amplitude underestimated.
MMRP-106. A blend in ASAS-SN data, amplitude underestimated. In
the data for z![]() , z
, z![]() , and a
, and a![]() bands, the brightening trend was
excluded before the amplitude analysis, its full amplitude being
0.018 (z
bands, the brightening trend was
excluded before the amplitude analysis, its full amplitude being
0.018 (z![]() ), 0.021 (z
), 0.021 (z![]() ), and 0.110 (a
), and 0.110 (a![]() ). In the a
). In the a![]() -band
data (an earlier time interval), the trend was not detected.
-band
data (an earlier time interval), the trend was not detected.
MMRP-107. An additional non-radial pulsation ![]() with the
following light elements (ASAS-SN and ZTF data):
with the
following light elements (ASAS-SN and ZTF data):
![]() HJD(max) = 2458888.032 + 0
HJD(max) = 2458888.032 + 0![]() 05108950
05108950 ![]() ;
;
the semi-amplitude ![]() is 0.012 (a
is 0.012 (a![]() ), 0.012 (a
), 0.012 (a![]() ),
0.007 (z
),
0.007 (z![]() ), 0.010 (z
), 0.010 (z![]() );
); ![]() -
-![]() = 0.45.
= 0.45.
Light elements for the CSS (JD 2453568-2456446) and 1SWASP (JD 2453860-2454615) time intervals:
![]()
![]() : HJD(max) = 2455055.0333 + 0
: HJD(max) = 2455055.0333 + 0![]() 0767249
0767249
![]() ;
;
![]()
![]() : HJD(max) = 2455055.0225 + 0
: HJD(max) = 2455055.0225 + 0![]() 0515180
0515180
![]() ;
;
![]()
![]() : HJD(max) = 2455055.0406 + 0
: HJD(max) = 2455055.0406 + 0![]() 0510897
0510897
![]() .
.
The magnitude ranges and semi-amplitudes according to 1SWASP and
CSS data: 13![]() 52-13
52-13![]() 82 (C
82 (C![]() ), 13
), 13![]() 85-14
85-14![]() 18 (1SWASP
mag);
18 (1SWASP
mag); ![]() is 0.068 (C
is 0.068 (C![]() ), 0.058 (1SWASP mag);
), 0.058 (1SWASP mag); ![]() is 0.018
(C
is 0.018
(C![]() ), 0.015 (1SWASP mag);
), 0.015 (1SWASP mag); ![]() is 0.013 (C
is 0.013 (C![]() ), 0.007 (1SWASP
mag).
), 0.007 (1SWASP
mag).
MMRP-108. The first-overtone period ![]() possibly varies. Light
elements for the CSS time interval:
possibly varies. Light
elements for the CSS time interval:
![]()
![]() : JD(max) = 2455055.0276 + 0
: JD(max) = 2455055.0276 + 0![]() 0644806
0644806
![]() ;
;
![]()
![]() : JD(max) = 2455055.0075 + 0
: JD(max) = 2455055.0075 + 0![]() 0502488
0502488
![]() .
.
The magnitude range and semi-amplitudes: 15![]() 18-15
18-15![]() 61
(C
61
(C![]() ),
), ![]() ,
, ![]() .
.
MMRP-109. The amplitude of the first-overtone oscillation varies from season to season, the mean estimates of the amplitude are given in the Table.
MMRP-110. A blend in ASAS-SN data, results of this analysis are
not given in the Tables. In these data, the second-overtone
frequency ![]() is not detected (as a result of possible large
errors of observations).
is not detected (as a result of possible large
errors of observations).
4. Discussion
4.1. Re-classification of MMRP-010
In the first part of the MMRP catalog (Khruslov 2023), I made a
wrong classification of MMRP-010 as a quadruple-mode D0123-type
variable. For this star, the frequencies of the supposed radial
modes are equidistant,
![]() .
Frequencies
.
Frequencies ![]() and
and ![]() are not in doubt, but the frequencies
are not in doubt, but the frequencies
![]() and
and ![]() of this equidistant quadruplet can be considered
interaction frequencies of the two main oscillations:
of this equidistant quadruplet can be considered
interaction frequencies of the two main oscillations:
![]() and
and ![]() .
.
Thus, in this case, we have two main frequencies ![]() and
and ![]() ;
in addition to them, interaction frequencies
;
in addition to them, interaction frequencies ![]() ,
,
![]() ,
, ![]() ,
, ![]() and
and ![]() are also
detected (in the order of decreasing amplitude).
are also
detected (in the order of decreasing amplitude).
Usually, the frequencies ![]() and especially
and especially ![]() have very small amplitudes and are very rarely detected in data
analysis. It is possible that the oscillations in these
interaction frequencies are amplified when they coincide with the
expected frequencies of the second and third overtones.
have very small amplitudes and are very rarely detected in data
analysis. It is possible that the oscillations in these
interaction frequencies are amplified when they coincide with the
expected frequencies of the second and third overtones.
For this reason, we re-classified MMRP-010 as a D01-type star. The real D0123 quadruplets (see 14 Galactic-bulge cases in Netzel et al. 2022) are not equidistant. In this paper, I also present a new real case of a D0123 type star, MMRP-078.
Among other features of MMRP-010, the inverted asymmetry
(![]() -
-![]() = 0.55) of its first-overtone light curve is worth
noting.
= 0.55) of its first-overtone light curve is worth
noting.
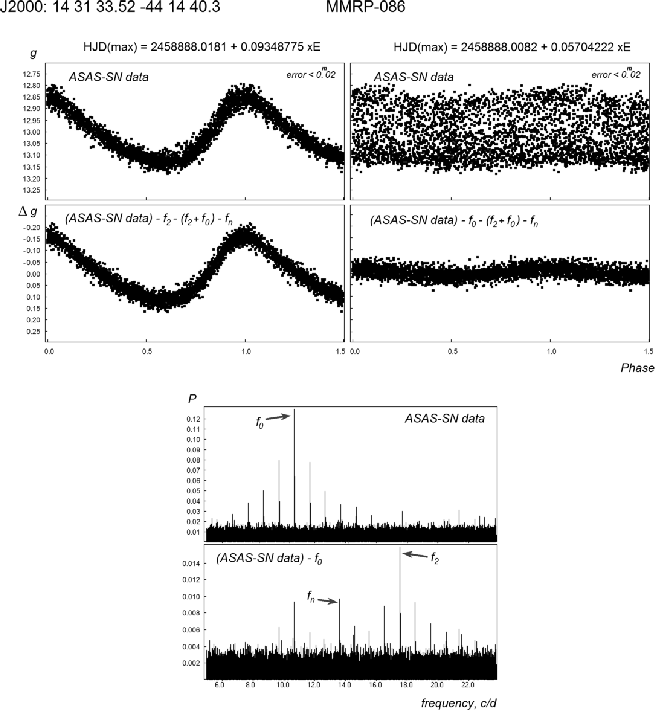
4.2. Pulsation modes of MMRP-086
MMRP-086 was classified as a ![]() Scuti star pulsating in the
fundamental and second overtone modes with an additional
non-radial pulsation (D02n type). In this case, the additional
non-radial pulsation
Scuti star pulsating in the
fundamental and second overtone modes with an additional
non-radial pulsation (D02n type). In this case, the additional
non-radial pulsation ![]() was found with certainty in the
was found with certainty in the
![]() -band ASAS-SN data, but it is not detected or uncertain in the
other photometric data (
-band ASAS-SN data, but it is not detected or uncertain in the
other photometric data (![]() -band ASAS-SN and 1SWASP). The period
ratio
-band ASAS-SN and 1SWASP). The period
ratio ![]() = 0.7857 may correspond to the
= 0.7857 may correspond to the ![]() ratio,
but
ratio,
but ![]() = 0.7766 does not correspond to the
= 0.7766 does not correspond to the ![]() ratio.
Therefore, I do not consider
ratio.
Therefore, I do not consider ![]() as a pulsation in the first
overtone and do not classify the star as D012 type. The light
curves and power spectra of the star MMRP-086 are displayed in
Fig. 2.
as a pulsation in the first
overtone and do not classify the star as D012 type. The light
curves and power spectra of the star MMRP-086 are displayed in
Fig. 2.
4.3. Variables with amplitude modulation
For 4 variables, amplitude modulation with slow changes (from one season to another) was detected. The variability type of these stars contains the index "m". Among these variables, there are two D01m stars (MMRP-091 and MMRP-109), one D12m star (MMRP-082 = V611 Cam), and one D13m star (MMRP-069).
In some cases, a periodic amplitude variation is possible;
however, also in a number of cases, it can represent mode
switching. For example, in the case of MMRP-091, during the last
time interval, the first-overtone oscillation was not detected,
mode switching is possible, type D01![]() D0 is not excluded.
Follow-up monitoring of the object is necessary.
D0 is not excluded.
Follow-up monitoring of the object is necessary.
4.4. The Petersen diagram
The Petersen diagram for all detected MMRP variables is displayed in Fig. 3. The diagram shows sequences corresponding to individual types of multi-periodic radially pulsating variables.
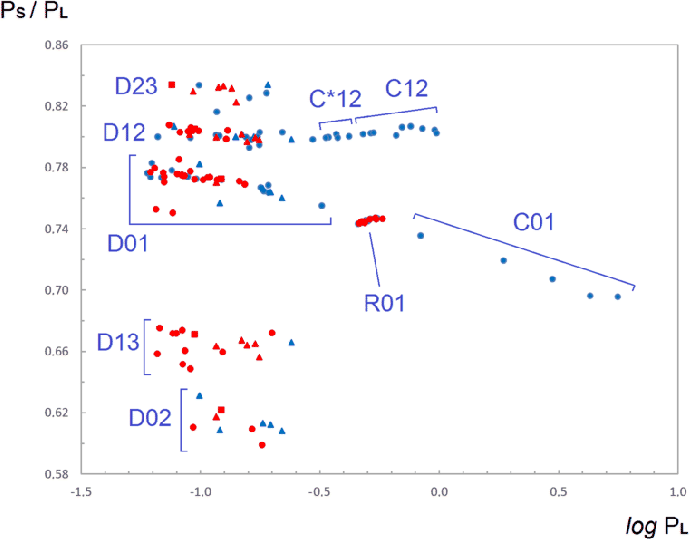 |
Fig. 3. The Petersen diagram for the multi-periodic stars of the MMRP catalog: blue - stars of the MMRP-I catalog, red - stars of the MMRP-II catalog (this paper); circles - double-mode stars, triangles - triple-mode stars, squares - quadruple-mode variables. |
4.5. A note to this paper
When this paper was already submitted to Peremennye Zvezdy, Jia et
al. (2024) published a catalogue of multimode ![]() Sct stars
from the Zwicky Transient Facility Survey. A number of stars from
our publication were included in this work. These are objects MMRP
051-057, 059, 060, 062, 064, 066, 067, 070, 071, 074, 076-079,
082, 104, 105, and 110. In most cases, the results (classification
of pulsation modes and light elements) are almost identical.
However, MMRP-104 was classified by Jia et al. (2024) as a
triple-mode pulsating star that varied in the fundamental, first-
and second-overtone modes, while I identified the third pulsation
as a non-radial mode (because of the period ratio
Sct stars
from the Zwicky Transient Facility Survey. A number of stars from
our publication were included in this work. These are objects MMRP
051-057, 059, 060, 062, 064, 066, 067, 070, 071, 074, 076-079,
082, 104, 105, and 110. In most cases, the results (classification
of pulsation modes and light elements) are almost identical.
However, MMRP-104 was classified by Jia et al. (2024) as a
triple-mode pulsating star that varied in the fundamental, first-
and second-overtone modes, while I identified the third pulsation
as a non-radial mode (because of the period ratio
![]() ) and gave the star the D01n type; MMRP-105 was
classified by Jia et al. (2024) as a double-mode
) and gave the star the D01n type; MMRP-105 was
classified by Jia et al. (2024) as a double-mode ![]() Scuti
star pulsating in the first and second overtones, while I give the
type D123 (the third-overtone mode is real, see power spectra in
the z
Scuti
star pulsating in the first and second overtones, while I give the
type D123 (the third-overtone mode is real, see power spectra in
the z![]() and z
and z![]() bands). Also, the cited authors did not detect
the amplitude modulation of MMRP-082.
bands). Also, the cited authors did not detect
the amplitude modulation of MMRP-082.
Additionally, for seven of these stars (MMRP-054, 056, 062, 067, 076, 082, and 105), I used data from ASAS-SN to improve their light elements.
Acknowledgments: The author wishes to thank Dr. V.P.
Goranskij for providing his software.
References:
Bellm, E. C., Kulkarni, S. R., & Graham, M. J. 2019, Publ. Astron. Soc. Pacific, 131, 018002
Butters, O. W., West, R. G., Anderson, D. R., et al. 2010, Astron. & Astrophys., 520, L10
Chen, X., Wang, S., Deng, L., et al. 2020, Astrophys. J., Suppl. Ser., 249, id. 18
Drake, A. J., Djorgovski, S. G., Mahabal, A., et al. 2009, Astrophys. J., 696, 870
Gaia Collaboration, Brown, A.G.A., Vallenari, A., Prusti, T., et al. 2018, Astron. & Astrophys., 616, id. A1
Gaia Collaboration, 2022, Gaia DR3 Part 4. Variability, VizieR On-line Data Catalog: I/358
Jayasinghe, T., Kochanek, C. S., Stanek, K. Z., et al. 2018, Mon. Notices Roy. Astron. Soc., 477, 3145
Jayasinghe, T., Kochanek, C. S., Stanek, K. Z., et al. 2021, Mon. Notices Roy. Astron. Soc., 503, 200
Jayasinghe, T., Stanek, K. Z., & Kochanek, C. S. 2019a, Mon. Notices Roy. Astron. Soc., 486, 1907
Jayasinghe, T., Stanek, K. Z., & Kochanek, C. S. 2019b, Mon. Notices Roy. Astron. Soc., 485, 961
Jayasinghe, T., Stanek, K. Z., & Kochanek, C. S. 2020, Mon. Notices Roy. Astron. Soc., 491, 13
Jia, Q., Chen, X., Wang, S., et al. 2024, Astrophys. J., Suppl. Ser., 273, id. 7
Khruslov, A. V. 2023, Perem. Zvezdy, 43, No. 7, 55
Kochanek, C. S., Shappee, B. J., Stanek, K. Z., et al. 2017, Publ. Astron. Soc. Pacific, 129, 104502
Malanchev, K. L., Pruzhinskaya, M. V., Korolev, V. S., et al. 2021, Mon. Notices Roy. Astron. Soc., 502, 5147
Masci, F. J., Laher, R. R., & Rusholme, B. 2019, Publ. Astron. Soc. Pacific, 131, 018003
Netzel, H., Pietrukowicz, P., Soszynski, I., & Wrona, M. 2022, Monthly Notices Roy. Astron. Soc., 510, 1748
Petersen, J. O. 1973, Astron. & Astrophys., 27, 89
Petersen, J. O., & Christensen-Dalsgaard, J. 1996, Astron. & Astrophys., 312, 463
Samus, N. N., Kazarovets, E. V., Durlevich, O. V., Kireeva, N. N., Pastukhova, E. N. 2017, Astron. Rep., 61, 80
Shappee, B. J., Prieto, J. L., Grupe, D., et al. 2014, Astrophys. J., 788, 48
Smolec, R. & Moskalik, P. 2010, Astron. & Astrophys., 524, A40
Sokolovsky, K. V., 2007, Perem. Zvezdy Prilozh., 7, No. 30
4.6. Supplement Tables
| No. | Semi-amplitudes | Magnitude ranges | ||||||
| a |
a |
z |
z |
a |
a |
z |
z |
|
| 010 | 0.143 | 0.164 | 0.112 | 0.162 | 14.00- | 14.37- | 13.68- | 14.32- |
| 0.120 | 0.136 | 0.102 | 0.130 | 14.74 | 15.21 | 14.26 | 15.17 | |
| 051 | - | - | 0.142 | 0.210 | - | - | 17.32- | 17.67- |
| - | - | 0.012 | 0.018 | 17.71 | 18.24 | |||
| 052 | - | - | 0.089 | 0.139 | - | - | 17.51- | 17.84- |
| - | - | 0.035 | 0.054 | 17.89 | 18.43 | |||
| 053 | - | - | 0.095 | 0.140 | - | - | 17.12- | 17.63- |
| - | - | 0.117 | 0.162 | 17.72 | 18.50 | |||
| 054 | - | - | 0.121 | 0.183 | - | - | 15.85- | 16.05- |
| - | - | 0.009 | 0.017 | 16.15 | 16.50 | |||
| 055 | - | - | 0.043 | 0.060 | - | - | 16.23- | 17.33- |
| - | - | 0.079 | 0.112 | 16.56 | 17.83 | |||
| 056 | 0.033 | 0.045 | 0.023 | 0.035 | 15.18- | 15.44- | 14.99- | 15.47- |
| 0.115 | 0.131 | 0.087 | 0.140 | 15.72 | 16.00 | 15.32 | 15.90 | |
| 0.014: | 0.012 | 0.016 | ||||||
| 057 | - | - | 0.115 | 0.170 | - | - | 16.97- | 17.18- |
| - | - | 0.023 | 0.031 | 17.31 | 17.69 | |||
| 058 | - | - | 0.132 | 0.179 | - | - | 15.91- | 16.02- |
| - | - | 0.159 | 0.222 | 16.60 | 16.97 | |||
| 059 | - | - | 0.053 | 0.080 | - | - | 17.76- | 19.27- |
| - | - | 0.042 | 0.063 | 18.08 | 19.73 | |||
| 060 | - | - | 0.181 | 0.245 | - | - | 17.19- | 17.77- |
| - | - | 0.017 | 0.029 | 17.73 | 18.52 | |||
| 061 | - | 0.118 | 0.103 | 0.154 | 16.2:- | 16.4- | 15.92- | 16.31- |
| - | 0.118 | 0.103 | 0.146 | 16.7: | 17.2 | 16.55 | 17.20 | |
| 062 | 0.225 | 0.245 | 0.173 | 0.239 | 13.47- | 13.58- | 13.58- | 13.55- |
| 0.015 | 0.025 | 0.018 | 0.031 | 14.06 | 14.25 | 14.03 | 14.20 | |
| 063 | - | - | 0.118 | 0.175 | - | - | 15.26- | 17.79- |
| - | - | 0.009 | 0.018 | 15.63 | 18.30 | |||
| 064 | - | - | 0.142 | 0.211 | - | - | 16.45- | 17.35- |
| - | - | 0.016 | 0.023 | 16.83 | 17.95 | |||
| 065 | - | - | 0.116 | 0.174 | - | - | 16.63- | 16.88- |
| - | - | 0.053 | 0.082 | 17.12 | 17.55 | |||
| 066 | - | - | 0.120 | 0.162 | - | - | 18.13- | 18.44- |
| - | - | 0.016 | 0.016: | 18.54 | 18.98 | |||
| 067 | 0.113 | 0.168 | 0.140 | 0.204 | 15.6- | 16.0- | 15.38- | 16.03- |
| 0.010 | 0.011 | 15.9 | 16.4 | 15.75 | 16.57 | |||
| 068 | - | - | 0.214 | 0.308 | - | - | 18.00- | 19.3- |
| - | - | 0.015 | 0.019: | 18.63 | 20.2 | |||
| 069 | - | - | 0.153 | 0.221 | - | - | 16.52- | 17.34- |
| - | - | 0.024 | 0.042 | 16.96 | 17.95 | |||
| 070 | - | - | 0.070 | 0.105 | - | - | 16.62- | 17.59- |
| - | - | 0.015 | 0.018 | 16.84 | 17.93 | |||
| 071 | - | - | 0.059 | 0.086 | - | - | 18.10- | 19.27- |
| - | - | 0.053 | 0.070 | 18.45 | 19.85 | |||
| 072 | - | - | 0.099 | 0.145 | - | - | 17.43- | 18.32- |
| - | - | 0.026 | 0.042 | 17.77 | 18.85 | |||
| 073 | - | - | 0.065 | 0.093 | - | - | 16.34- | 16.94- |
| - | - | 0.019 | 0.028 | 16.56 | 17.24 | |||
| 074 | - | - | 0.152 | 0.248 | - | - | 18.09- | 19.83- |
| - | - | 0.054 | 0.101 | 18.63 | 20.85 | |||
| 075 | 0.150 | 0.170 | 0.101 | 0.168 | 13.69- | 14.00- | 13.56- | 13.92- |
| 0.044 | 0.063 | 0.042 | 0.061 | 14.20 | 14.59 | 13.93 | 14.45 | |
| 076 | 0.097: | 0.109: | 0.120 | 0.167 | 15.65- | 16.0- | 15.64- | 16.45- |
| 0.018: | 0.017: | 0.017 | 0.023 | 16.05: | 16.5 | 15.97 | 16.90 | |
| 077 | - | - | 0.119 | 0.176 | - | - | 17.02- | 17.86- |
| - | - | 0.012 | 0.016 | 17.37 | 18.38 | |||
| 078 | - | - | 0.051 | 0.068 | - | - | 16.27- | 17.11- |
| - | - | 0.057 | 0.083 | 16.60 | 17.56 | |||
| - | - | 0.023 | 0.033 | |||||
| - | - | 0.029 | 0.042 | |||||
| 079 | - | - | 0.137 | 0.200 | - | - | 17.41- | 18.09- |
| - | - | 0.018 | 0.021 | 17.83 | 18.70 | |||
| 080 | - | - | 0.177 | 0.234 | - | - | 16.60- | 16.59- |
| - | - | 0.042 | 0.058 | 17.17 | 17.42 | |||
| 081 | 0.090 | 0.101 | 0.076 | 0.106 | 13.28- | 13.55- | 13.20- | 13.64- |
| 0.012 | 0.009 | 0.010 | 13.56 | 13.91 | 13.41 | 13.97 | ||
| 0.021 | 0.018 | 0.013 | 0.018 | |||||
| 082 | - | 0.232 | 0.157 | 0.224 | 13.67- | 13.69- | 13.73- | 13.72- |
| - | 0.032 | 0.023 | 0.035 | 14.06 | 14.30 | 14.15 | 14.33 | |
| 083 | 0.077 | 0.101 | - | - | 13.16- | 13.36- | - | - |
| 0.012 | 0.011 | - | - | 13.43 | 13.69 | |||
| 084 | - | - | 0.041 | 0.058 | - | - | 18.54- | 18.60- |
| - | - | 0.165 | 0.224 | 19.18 | 19.40 | |||
| 085 | - | - | 0.136 | 0.194 | - | - | 16.77- | 16.74- |
| - | - | 0.152 | 0.235 | 17.48 | 17.73 | |||
| 086 | 0.113 | 0.135 | - | - | 12.64- | 12.80- | - | - |
| 0.010 | 0.013 | - | - | 12.96 | 13.18 | |||
| 087 | 0.200 | 0.235 | - | - | 13.94- | 14.29- | - | - |
| 0.023 | 0.025 | - | - | 14.52 | 15.01 | |||
| 088 | - | - | 0.038 | 0.057 | - | - | 19.27- | 19.32- |
| - | - | 0.149 | 0.216 | 19.85 | 20.15 | |||
| 089 | 0.093 | 0.102 | - | - | 13.15- | 13.61- | - | - |
| 0.028 | 0.037 | - | - | 13.55 | 14.10 | |||
| 0.034 | 0.040 | - | - | |||||
| 090 | - | - | 0.128 | 0.182 | - | - | 17.00- | 16.99- |
| - | - | 0.156 | 0.220 | 17.79 | 18.01 | |||
| 091 | 0.141 | - | - | - | 13.90- | 14.33- | - | - |
| 0.071 | - | - | - | 14.55 | 14.92 | |||
| 092 | - | - | 0.023 | 0.033 | - | - | 17.20- | 17.29- |
| - | - | 0.159 | 0.231 | 17.65 | 17.89 | |||
| 093 | - | - | 0.110 | 0.151 | - | - | 16.93- | 16.86- |
| - | - | 0.156 | 0.222 | 17.57 | 17.80 | |||
| 094 | 0.151 | 0.177 | 0.116 | 0.165 | 12.83- | 13.14- | 12.65- | 13.13- |
| 0.014 | 0.020 | 0.010 | 0.020 | 13.23 | 13.61 | 12.95 | 13.55 | |
| 095 | - | - | 0.112 | 0.169 | - | - | 17.20- | 17.11- |
| - | - | 0.159 | 0.226 | 17.87 | 18.11 | |||
| 096 | 0.062 | 0.075 | - | - | 11.60- | 11.76- | - | - |
| 0.015 | 0.015 | - | - | 11.81 | 12.00 | |||
| 097 | 0.196 | 0.235 | - | - | 14.41- | 14.48- | - | - |
| 0.050 | 0.063 | - | - | 15.18 | 15.40 | |||
| 098 | - | - | 0.065 | 0.097 | - | - | 18.76- | 18.70- |
| - | - | 0.152 | 0.234 | 19.35 | 19.62 | |||
| 099 | 0.073 | 0.070 | 0.060 | 0.088 | 14.7- | 15.2- | 14.47- | 15.37- |
| 0.027 | 0.023 | 0.028 | 15.2 | 15.7 | 14.72 | 15.72 | ||
| 0.038 | 0.024 | 0.020 | 0.034 | |||||
| 100 | 0.082 | 0.099 | - | - | 12.17- | 12.38- | - | - |
| 0.023 | 0.028 | - | - | 12.52 | 12.83 | |||
| 0.038 | 0.043 | - | - | |||||
| 101 | - | - | 0.045 | 0.062 | - | - | 19.2- | 19.5- |
| - | - | 0.143 | 0.217 | 19.7 | 20.4 | |||
| 102 | 0.063 | 0.065 | - | - | 14.95- | 15.10- | - | - |
| 0.056 | 0.062 | - | - | 15.37 | 15.60 | |||
| 103 | 0.127 | 0.152 | 0.104 | 0.141 | 13.51- | 13.60- | 13.60- | 13.67- |
| 0.039 | 0.051 | 0.028 | 0.048 | 14.00 | 14.16 | 13.98 | 14.12 | |
| 104 | - | - | 0.075 | 0.108 | - | - | 17.23- | 17.58- |
| - | - | 0.081 | 0.110 | 17.69 | 18.25 | |||
| 105 | 0.105 | 0.128 | 0.108 | 0.174 | 13.75- | 14.05- | 13.73- | 14.41- |
| 0.011 | 0.014 | 0.012 | 0.018 | 14.08 | 14.50 | 14.05 | 14.87 | |
| 0.010 | 0.007 | 0.007 | 0.010 | |||||
| 106 | 0.039: | 0.041: | 0.077 | 0.128 | 14.6:- | 14.65:- | 15.17- | 15.67- |
| 0.011: | 0.006: | 0.010 | 0.013 | 14.75: | 14.85: | 15.41 | 16.03 | |
| 107 | 0.083 | 0.093 | 0.050 | 0.083 | 13.75- | 13.92- | 13.73- | 13.96- |
| 0.018 | 0.019 | 0.013 | 0.019 | 14.05 | 14.24 | 13.91 | 14.20 | |
| 108 | 0.088 | 0.110 | - | - | 15.10- | 15.15- | - | - |
| 0.087 | 0.115 | - | - | 15.65 | 15.80 | |||
| 109 | - | - | 0.081 | 0.104 | - | - | 17.18- | 17.54- |
| - | - | 0.062 | 0.091 | 17.61 | 18.12 | |||
| 110 | - | - | 0.180 | 0.259 | - | - | 16.06- | 16.84- |
| - | - | 0.018 | 0.024 | 16.53 | 17.52 | |||
| No. | ||||||
| 2MASS | APASS | APASS | ASAS-SN | ZTF | ||
| 010 | 0.47 | 0.91 | 0.72 | 0.45 | 0.82 | -2.9 |
| 051 | 0.24: | 0.48 | 0.50 | - | 0.46 | -9.1 |
| 052 | 0.46: | - | - | - | 0.47 | -6.0 |
| 053 | 0.53 | - | - | - | 0.69 | -5.9 |
| 054 | 0.29 | 0.46 | 0.25 | 0.23: | 0.29 | -9.1 |
| 055 | 0.69 | 0.76 | 1.12 | - | 1.19 | +2.1 |
| 056 | 0.35 | 0.75 | 0.53 | 0.30 | 0.55 | -5.1 |
| 057 | 0.55 | - | - | - | 0.31 | -8.4 |
| 058 | 0.47: | 0.42 | 0.27 | - | 0.27 | -12.0 |
| 059 | 0.90 | - | - | - | 1.60 | +1.6 |
| 060 | 0.59 | - | - | - | 0.69 | -7.5 |
| 061 | 0.40 | 0.59 | 0.57 | 0.45 | 0.62 | -4.0 |
| 062 | 0.17 | 0.39 | 0.08 | 0.17 | 0.11 | -15.2 |
| 063 | 0.33 | - | - | - | 0.60 | -6.0 |
| 064 | 0.42 | - | - | - | 1.02 | +5.9 |
| 065 | 0.63 | - | - | - | 0.37 | -10.2 |
| 066 | - | - | - | - | 0.39 | +9.1 |
| 067 | 0.53 | 1.09 | - | 0.46 | 0.77 | +2.6 |
| 068 | 0.73 | - | - | - | 1.41 | +5.0 |
| 069 | 0.58 | 0.51 | 0.57 | - | 0.90 | +1.7 |
| 070 | 0.65 | - | - | - | 1.04 | +4.5 |
| 071 | 0.97 | - | - | - | 1.30 | +5.0 |
| 072 | 0.37 | - | - | - | 0.98 | +3.8 |
| 073 | 0.38 | 0.68 | 0.58 | - | 0.63 | +10.7 |
| 074 | 0.91 | - | - | - | 1.99 | +0.9 |
| 075 | 0.36 | 0.72 | 0.58 | 0.36 | 0.45 | -12.5 |
| 076 | 0.45 | 0.93 | 0.76 | 0.37 | 0.86 | +4.0 |
| 077 | 0.69 | - | - | - | 0.93 | +1.1 |
| 078 | 0.71 | - | - | - | 0.90 | +4.1 |
| 079 | 0.43: | - | - | - | 0.78 | +5.0 |
| 080 | 0.16: | 0.41 | 0.20 | - | 0.19 | +18.1 |
| 081 | 0.39 | 0.61 | 0.44 | 0.33 | 0.51 | +7.7 |
| 082 | 0.18 | 0.27 | 0.10 | 0.15 | 0.11 | +27.5 |
| 083 | 0.20: | 0.42 | 0.28 | 0.23 | - | -5.9 |
| 084 | - | - | - | - | 0.13 | +74.4 |
| 085 | 0.74 | - | - | - | 0.14 | +48.5 |
| 086 | 0.21 | 0.44 | 0.24 | 0.21 | - | +15.0 |
| 087 | 0.45 | 0.89 | 0.78 | 0.44 | - | +7.4 |
| 088 | - | - | - | - | 0.18 | +45.2 |
| 089 | 0.60 | 1.06 | 1.02 | 0.49 | - | -4.8 |
| 090 | - | - | - | - | 0.14 | +34.5 |
| 091 | 0.29 | 0.61 | 0.40 | 0.34 | - | +11.2 |
| 092 | - | 0.03 | 0.54 | - | 0.16 | +44.8 |
| 093 | - | - | - | - | 0.10 | +37.6 |
| 094 | 0.39 | 0.72 | 0.74 | 0.35 | 0.57 | +18.7 |
| 095 | 1.25: | - | - | - | 0.11 | +39.8 |
| 096 | 0.22 | 0.60 | 0.27 | 0.17 | - | -0.5 |
| 097 | 0.17 | 0.40 | 0.20 | 0.18 | - | -15.9 |
| 098 | - | - | - | - | 0.12 | +27.6 |
| 099 | 1.23 | 0.97 | 0.91 | 0.45 | 0.94 | +0.9 |
| 100 | 0.23 | 0.35 | 0.18 | 0.27 | - | +14.5 |
| 101 | - | - | - | - | 0.53 | +10.8 |
| 102 | 0.23 | 0.45 | 0.17 | 0.20 | - | -14.1 |
| 103 | 0.15 | 0.33 | 0.04 | 0.16 | 0.12 | -16.4 |
| 104 | 0.84 | - | - | - | 0.51 | -4.0 |
| 105 | 0.41 | 0.96 | 0.71 | 0.40 | 0.76 | -2.7 |
| 106 | 0.44 | 0.80 | 0.50 | 0.09: | 0.58 | -3.7 |
| 107 | 0.21 | 0.44 | 0.28 | 0.20 | 0.24 | -24.1 |
| 108 | 0.39 | 0.21 | 0.09 | 0.10 | - | -37.0 |
| 109 | - | - | 0.30 | - | 0.43 | -8.1 |
| 110 | 0.49 | - | - | - | 0.91 | +2.2 |