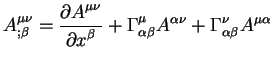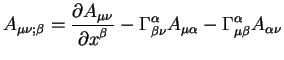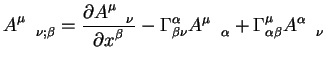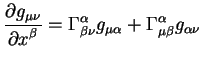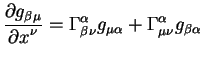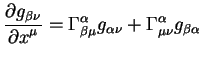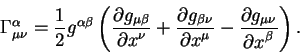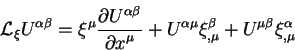<< 5. Неэвклидова геометрия | Оглавление | 7. Тензор кривизны >>
- 6.1 Ковариантное дифференцирование
- 6.2 Связь метрического тензора и символов Кристоффеля
- 6.3 Производная Лагранжа -Эйлера
- 6.4 Производная Ли
6. Анализ в неэвклидовой геометрии
Вычисление различных величин в общей теории относительности - это вычисление тензорных величин различного ранга (скалярных, векторных, тензорных второго ранга, иногда более высоких рангов), включая операции дифференцирования и интегрирования. В эвклидовой геометрии операция дифференцирования для, например, векторов, определялась так же как для обычных математических функций - скалярных величин. В неэвклидовой геометрии процедура построения производных от вектора является более сложной. Она носит название ковариантного дифференцирования.
6.1 Ковариантное дифференцирование
Напомним, что если в каждой точке некоторой области (которое может
охватывать и все пространство) задана некоторая скалярная или векторная
величина, то говорят, что задано поле этой величины. Аналогично можно
задать поле тензорной величины. Скажем метрика Минковского, определяемая
как (5.6), является тензорным полем второго ранга, определенным
во всех пространстве. Каждая компонента этого поля является постоянной
величиной, причем диагональные компоненты отличны от нуля (![]() ,
,
![]() ), а недиагональные равны нулю. Примером
тензорного поля второго ранга, которое не является постоянным может служить
метрика на поверхности сферы. Недиагональные компоненты такой метрики, как
и в предыдущем примере, равны нулю, но из диагональных компонент только
компонента
), а недиагональные равны нулю. Примером
тензорного поля второго ранга, которое не является постоянным может служить
метрика на поверхности сферы. Недиагональные компоненты такой метрики, как
и в предыдущем примере, равны нулю, но из диагональных компонент только
компонента ![]() , тогда как вторая компонента является функцией одной
из координат
, тогда как вторая компонента является функцией одной
из координат
![]() .
.
В пространстве с эвклидовой или псевдоэвклидовой метрикой в векторном и
тензорном анализе можно определить производные от соответствующего поля по
стандартным правилам:
В пространстве с эвклидовой метрикой разность двух векторов, даже взятых в различных точках пространства является вектором. Эта разность при линейных преобразованиях координат преобразуется как вектор.
При нелинейных преобразованиях координат или в пространстве с неэвклидовой метрикой разность двух векторов, взятых в различных точках пространства преобразуется уже не по закону преобразования векторов. Хотя подробное изложение правил тензорного анализа можно найти в прекрасных учебниках [8], [9], [10], мы посвятим несколько абзацев демонстрации особенностей нелинейных преобразований и преобразований в неэвклидовых пространствах.
Вначале покажем, что при нелинейных преобразованиях дифференциал векторного поля уже не является векторным полем.
Итак, введем стандартное обозначение:
и сделаем преобразование координат
Поле
Дифференциал вычисляется в точке
аналогичные вычисления проделаем для самого векторного поля:
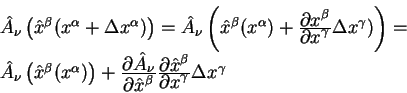
Все величины теперь вычислены в точке ![]() , поэтому можем строить
дифференциал и производную векторного поля по обычным правилам:
, поэтому можем строить
дифференциал и производную векторного поля по обычным правилам:
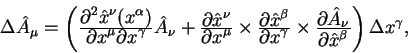
а производная этого векторного поля вычисляется как:
Второй член в этом уравнении обладает признаками тензора, преобразуется как тензорное поле второго ранга. Первое слагаемое явно не является тензорным полем, поскольку преобразуется по другим правилам.
Так получилось потому, что мы пренебрегли последовательными рассуждениями в
определении производных от векторнорго поля в неэвклидовой геометрии. При
вычислении приращения векторного поля мы вычитали величины определенные в
разных точках пространства. Первая величина определена в точке
![]() , а вторая в точке
, а вторая в точке ![]() . В эвклидовой геометрии
при вычислении приращения векторного поля обычно опускается промежуточный
шаг, который заключается в том, что векторы, заданные в соседних точках,
сводятся по определенным правилам в одну точку.
. В эвклидовой геометрии
при вычислении приращения векторного поля обычно опускается промежуточный
шаг, который заключается в том, что векторы, заданные в соседних точках,
сводятся по определенным правилам в одну точку.
Таким правилом является параллельный перенос. Дифференциал векторного поля,
полученный вычитанием значения векторного поля заданного в точке
![]() и параллельно перенесенного из точки
и параллельно перенесенного из точки ![]() в точку
в точку
![]() из значения векторного поля в точке
из значения векторного поля в точке
![]() называется ковариантным дифференциалом.
называется ковариантным дифференциалом.
Итак, для получения из тензорного поля ранга ![]() путем дифференцирования
тензорного поля ранга
путем дифференцирования
тензорного поля ранга ![]() необходимо вычислять не обычный дифференциал, а
ковариантный дифференциал.
необходимо вычислять не обычный дифференциал, а
ковариантный дифференциал.
6.1.1 Параллельный перенос вектора
Ковариантное дифференцирование тесно связано с понятием параллельного переноса вектора.
Параллельный перенос вектора в эвклидовом пространстве определяется как перенос вдоль некоторой прямой таким образом, что угол между вектором и прямой остается при переносе постоянным. Соответственно, компоненты вектора при таком переносе остаются неизменными.
В неэвклидовой геометрии эта операция несколько изменяется. Аналогом прямой в неэвклидовой геометрии является геодезическая линия. Параллельный перенос вектора определяется как перенос вдоль геодезической линии, которая соединяет две точки. Естественно, как и в эвклидовой геометрии, угол между переносимым вектором и геодезической линией остается постоянным.
В качестве характеристики угла между выбранным вектором, скажем,
![]() и геодезической линией принимем угол между вектором
и геодезической линией принимем угол между вектором
![]() и вектором касательным к геодезической линии. Таким вектором
является производная от уравнений геодезической линии по афинному параметру
вдоль этой линии
и вектором касательным к геодезической линии. Таким вектором
является производная от уравнений геодезической линии по афинному параметру
вдоль этой линии
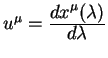 . Угол
между
. Угол
между ![]() и
и ![]() определяется согласно
уравнению (5.8). Пусть норма вектора
определяется согласно
уравнению (5.8). Пусть норма вектора
![]() равна единице6.1. Прежде чем вести вычисления,
заметим, что при параллельном переносе скалярные величины не
меняются6.2. Поэтому скалярное произведение двух векторов
тоже остается постоянным при параллельном переносе, а значит и норма одного
вектора постоянна при таком переносе. Поэтому требование постоянства угла
между вектором
равна единице6.1. Прежде чем вести вычисления,
заметим, что при параллельном переносе скалярные величины не
меняются6.2. Поэтому скалярное произведение двух векторов
тоже остается постоянным при параллельном переносе, а значит и норма одного
вектора постоянна при таком переносе. Поэтому требование постоянства угла
между вектором ![]() и вектором
и вектором ![]() можно заменить на
требование постоянства скалярного произведения этих векторов.
можно заменить на
требование постоянства скалярного произведения этих векторов.
Итак вычислим изменение произвольного вектора ![]() при параллельном
переносе вдоль геодезической линии. Основное требонание, налагаемое
параллельным перносом заключается в том, что скалярное произведение вектора
при параллельном
переносе вдоль геодезической линии. Основное требонание, налагаемое
параллельным перносом заключается в том, что скалярное произведение вектора
![]() и вектора касательного к геодезической линии является
постоянным вдоль линии переноса:
и вектора касательного к геодезической линии является
постоянным вдоль линии переноса:
Введем обозначение для изменения компонент
![]() вектора при
параллельном переносе. Теперь распишем уравнение сохрания скалярного
произведения более подробно
вектора при
параллельном переносе. Теперь распишем уравнение сохрания скалярного
произведения более подробно
Преобразуем правую часть уравнения, выделив член нулевого порядка малости
по бесконечно малому смещению и два члена первого порядка малости, вторым
порядком малости здесь будем пренебрегать. Первый член в правой части
сократится с членом, который стоит в левой части, а два члена первого
порядка малости дадут уравнение для вычисления
![]() :
:
Подставим в это уравнение изменение касательного вектора вдоль
геодезической (5.13) и получим уравнение для изменения вектора
![]() :
:
Отсюда получаем решение:
В современных [10] и классических курсах [8] по общей теории относительности уравнение для вычисления изменений компонент вектора при параллельном перносе выводится методом переноса вдоль прямой в касательном пространстве [10] или в галилеевых координатах [8]. Эти две операции эквивалентны. Параллельный перенос приводит к тому, что компоненты вектора меняются.
Ковариантный дифференциал будем обозначать большой буквой ![]() латинского
алфавита. Ковариантный дифференциал векторного поля
латинского
алфавита. Ковариантный дифференциал векторного поля ![]() является
разностью двух малых величин. Первая - обычный дифференциал поля
является
разностью двух малых величин. Первая - обычный дифференциал поля ![]() между двумя пространственно - временными точками
между двумя пространственно - временными точками ![]() , вторая
величина - изменение векторного поля
, вторая
величина - изменение векторного поля
![]() при параллельном
переносе его из одной точки пространства в другую.
при параллельном
переносе его из одной точки пространства в другую.
Контравариантные компоненты
![]() от ковариантных отличаются
знаком:
от ковариантных отличаются
знаком:
Теперь можно написать уравнения для ковариантных дифференциалов
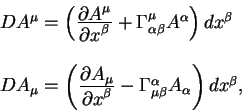
а также уравнения для ковариантных производных от векторов
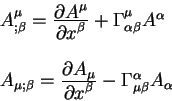
Знак ";" означает ковариантную производную. Мы будем в дальнейшем использовать этот знак "точка с запятой" для обозначения ковариантной производной, а для обозначения обычной производной будем использовать знак "," - "запятая".
Легко видеть, что ковариантный дифференциал ![]() подчиняется всем
основным правилам дифференцирования:
подчиняется всем
основным правилам дифференцирования:
пользуясь этими правилами можно доказать правило образования ковариантных производных от тензоров более высокого ранга чем вектора:
Обратим внимание, что в случае смещанных индексов порядок может быть важен, в том случае, когда тензор не является симметричным. Тогда указание на то, что индекс должен следовать вторым показано отступом, верхний и нижний индексы не расположены в одной колонке. То же самое справедливо и для символом Кристоффеля.
Теперь можно просто сформулировать словесное правило образования ковари
антной производной от тензора любого ранга и содержащего произвольное
количество нижних и верхних индексов. Ковариантная производная равняется
сумме частной производной от тензора по некоторой координате плюс (или
минус) произведения символов Кристоффеля на сам тензор. Количество членов в
этой сумме равняется количеству индексов плюс частная производная от самого
тензора. Более точно, ковариантная производная от тензора ранга ![]() ,
содержащего
,
содержащего ![]() верхних и
верхних и ![]() нижних индексов равняется частной производной
от этого тензора, плюс произведение символа Кристоффеля (с верхним
индексом таким же как один из верхних индексов дифференцируемого тензора и
одним из нижних индексов таких же как у координаты, по которой ведется
дифференцирование) с самим тензором у которого один из верхних индексов
суммируется со вторым индексом символа Кристоффеля, минус
произведение символа Кристофферя (теперь верхний индекс у связности
является немым индексом суммирования, а один из нижних индексов такой же
как у координаты по которой ведется дифференцирование) с самим тензором у
которого очередный нижний индекс заменен на нем ой индекс суммирования, а
остальные расположены по порядку.
нижних индексов равняется частной производной
от этого тензора, плюс произведение символа Кристоффеля (с верхним
индексом таким же как один из верхних индексов дифференцируемого тензора и
одним из нижних индексов таких же как у координаты, по которой ведется
дифференцирование) с самим тензором у которого один из верхних индексов
суммируется со вторым индексом символа Кристоффеля, минус
произведение символа Кристофферя (теперь верхний индекс у связности
является немым индексом суммирования, а один из нижних индексов такой же
как у координаты по которой ведется дифференцирование) с самим тензором у
которого очередный нижний индекс заменен на нем ой индекс суммирования, а
остальные расположены по порядку.
Коваринтные производные подчиняются тем же обычным правилам дифференцирования, которые справедливы для обычных производных от векторных и тензорных полей в эвклидовам пространстве. Эти правила перечислены чуть выше для вариаций вектора (см. уравнение (6.2)).
Добавим, что ковариантная производная от скалярного поля совпадает с обычной производной.
Законы преобразований символов Кристоффеля при преобразованиях координат
имеют вид:
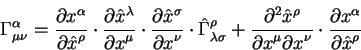
В обычной неэвклидовой геометрии предпологается, что символ Кристоффеля является симметричным по нижним индексам.
Существует обобщения неэвклидовой геометрии в которой символ Кристоффеля
уже не является симметричным. Разность
называется тензором кручения. В отличие от символа Кристоффеля, который не
является тензором и преобразуется по закону, содержащему вторую производную
от координат, величина
![]() является тензором и, как
легко проверить, преобразуется как тензор третьего ранга.
является тензором и, как
легко проверить, преобразуется как тензор третьего ранга.
В общей теории относительности тензор кручения равен нулю, эксперименты
показывают, что введение этой величины излишне. Поэтому далее мы не будем
рассматривать тензор кривизны и его наблюдательные проявления.
В общей теории относительности символ Кристоффеля является
симметричным по нижним индексам, что выражается уравнением вида
![]() . Всюду ниже будем
полагать, что
. Всюду ниже будем
полагать, что
![]() является симметричным по индексам
является симметричным по индексам
![]() .
.
6.2 Связь метрического тензора и символов Кристоффеля
Для вычисления ковариантных производных в неэвклидовой геометрии необходимо
научиться вычислять символы Кристоффеля. Они вычисляются очень просто в
метрических пространствах, когда
![]() определяется
через метрический тензор. Найдем связь
определяется
через метрический тензор. Найдем связь
![]() с
метрическим тензором.
с
метрическим тензором.
Ковариантный дифференциал является тензором, поэтому согласно правилу
поднятия и опускания индексов в метрических пространствах можно написать
уравнение:
Теперь продифференцирум (6.9) и применим правила (6.2).
Получим уравнение вида
Из сравнений уравнений (6.8) и (6.10) видно,
что ковариантный дифференциал от метрического тензора равен нулю.
Следовательно равны нулю ковариантные производные по всем координатам.
Вычислим ковариантные производные в явном виде согласно уравнению
(6.5). Эти ковариантные производные имеют вид:
Поскольку левая часть уравнения (6.11) равна нулю, как это следует из
уравнения (6.10), то и правая тоже равна нулю. В результате
получаем линейное уравнение для связи символов Кристоффеля с метрическим
тензором и его частными производными первого порядка:
Переставляя индексы в уравнении (6.12) получаем систему линейных уравнений вида:
Вычитая почленно из уравнения (6.13) уравнения (6.14) и
(6.15), получаем уравнение
из которого легко находим связь символов Кристоффеля с метрическим тензором
и его первыми производными по координатам:
Как видно из уравнения (5.11) эти два символа совпадают.
6.2.1 Ковариантная производная 4x скорости
Рассмотрим теперь ковариантную производную одного из самых важных для нас
векторов - 4![]() скорости пробной частицы или вектора касательного к
геодезической линии. Ковариантный дифференциал этого вектора есть:
скорости пробной частицы или вектора касательного к
геодезической линии. Ковариантный дифференциал этого вектора есть:
Теперь можно вычислить частную ковариантную производную по одной из
координат:
в соответствии с общими правилами ковариантного дифференцирования. Умножим
это уравнение на сам вектор 4![]() скорости:
скорости:
Первый член в правой части этого уравнения, как легко видеть, равен полной
производной от скорости по афинному параметру вдоль геодезической линии:
Оба члена вместе представляют уравнение геодезической линии, откуда имеем
еще один вид уравнения геодезической:
6.3 Производная Лагранжа -Эйлера
В математическом анализе и геометрии используют еще несколько видов производных. Для нас важными являются две из них, это производная Лагранжа -Эйлера и производная Ли. Вначале познакомимся с производной Лагранжа -Эйлера.
Рассмотрим множество функций
![]() координат
координат ![]() .
Эти функции могут быть компонентами скаляра, вектора или тензора. Они могут
быть объектами другой природы, которые преобразуются к другой системе
координат по собственным правилам. Для вычисления производной Лагранжа -Эйлера
неважна природа этих функций. Мы опустим индекс
.
Эти функции могут быть компонентами скаляра, вектора или тензора. Они могут
быть объектами другой природы, которые преобразуются к другой системе
координат по собственным правилам. Для вычисления производной Лагранжа -Эйлера
неважна природа этих функций. Мы опустим индекс ![]() , но будем помнить, что
функции
, но будем помнить, что
функции ![]() представляют из себя набор функций.
представляют из себя набор функций.
Рассмотрим функцию ![]() от аргументов, которые сами являются функциями и
их производными:
от аргументов, которые сами являются функциями и
их производными:
Еще раз подчеркнем, что ![]() в общем случае является множеством функций,
а не обязательно одной функцией.
в общем случае является множеством функций,
а не обязательно одной функцией.
Рассмотрим теперь функционал, например действие от функции ![]() :
:
взятое по некоторой 4![]() области
области ![]() .
.
Обозначим ![]() вариацию поля
вариацию поля ![]() и будем считать, что вариации
самого поля, а также всех его производных исчезают на границе области
и будем считать, что вариации
самого поля, а также всех его производных исчезают на границе области
![]() .
.
Вариации функции ![]() имеют вид:
имеют вид:
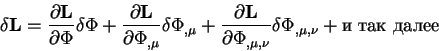
Отсюда получаем для вариаций функционала уравнение вида:
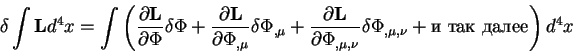
Интегрируя каждый из членов в круглых скобках по частям получаем:
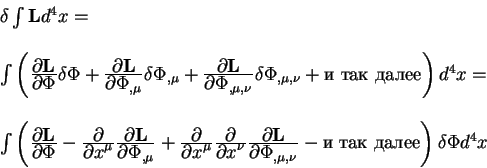
Выражение, которое находится в круглых скобках в последней строчке
называется производной Лагранжа -Эйлера. Итак по определению величина:
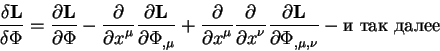
называется производной Лагранжа -Эйлера от L. Она тесно связана c функциональной или вариационной производной вводимой в теории случайных полей [11].
Уравнение вида:
называется уравнением Эйлера. Уравнения такого вида являются уравнениями
движения в ньютоновской механике. Иногда в качестве величины ![]() выступает переменная, которая вообще не преобразуется.
выступает переменная, которая вообще не преобразуется.
6.4 Производная Ли
Производная Ли для нас не так важна, как производная Лагранжа - Эйлера, но все же мы кратко проанализируем ее здесь, поскольку будем обращаться к ней несколько раз в течение курса. Более подробно о методе Ли и его применениях будет рассказано ниже.
Производная Ли играет большое значение при исследовании свойств симметрии метрики. Для исследования этих свойств напомним вначале простейшее понятие симметрии, например зеркальной симметрии. Геометрическое тело называют симметричным относительно плоскости, если эта плоскость разбивает тело на две части, из которых каждая является зеркальным отражением другой относительно этой плоскости. Сама плоскость в этом случае называется плоскостью симметрии. Зеркальной симметрией обладают многие предметы из окружающего нас мира: самолет, лист клена, форма человеческого тела (внутреннее строение уже не обладает свойством зеркальной симметрии!).
С формальной точки зрения зеркальную симметрию определяют как
форминвариантность относительно преобразования координат вида:
Если при таком преобразовании координат форма тела остается неизменной, то
говорят, что геометрическое тело симметрично относительно плоскости ![]()
Отметим, что приведенное выше преобразование не является непрерывным относительно некоторого параметра, как в большинстве случаев, которые мы рассматривали при преобразованиях координат в неэвклидовой геометрии. Поэтому свойства симметрии геометрических тел, точнее функций связаны с инвариантностью при преобразованиях координат. Зеркальная симметрия относиться к так называемым дискретным видам симметрии.
Ниже мы будем рассматривать только точечные виды симметрии. Они связаны с непрерывными преобразованиями, непрерывно зависят от одного или нескольких параметров. К таким видам симметрии относится, например, симметрия относительно вращения. Так, сфера - идеальный объект в трехмерном пространстве для изучения группы вращений. Вращения можно осуществлять на произвольный, сколь угодно малый, угол.
Определим понятие симметрии для метрического тензора. Говорят, что метрика
![]() является форминвариантной относительно преобразований
координат вида
является форминвариантной относительно преобразований
координат вида
![]() , если преобразованная
метрика
, если преобразованная
метрика
![]() - та же функция от
аргумента
- та же функция от
аргумента
![]() , что и первоначальная функция
, что и первоначальная функция
![]() от ее первоначального аргумента
от ее первоначального аргумента ![]() , т.е. [12]
, т.е. [12]
Заметим, что это равенство можно также переписать в двух эквивалентных формулировках:
и
Многие геометрические свойства пространства можно определить пользуясь понятиями симметрии. Симметрии пространства также важны для определения физических свойств, законов сохранения, поиска наиболее общих интегралов уравнений движения. Свойства метрики пространства - времени можно определить не прибегая к решению уравнений общей теории относительности, а пользуясь только соображениями симметрии. Поясним как это можно сделать на примере производных Ли.
Производные Ли являются обощениями понятия производных по направлению на
тензоры. Рассмотрим две точки в пространстве ![]() и
и ![]() , разделенные
малым расстоянием. Пусть координаты этих точек соединяются бесконечно
малым вектором, квадратом которого можно пренебречь по сравнению с
самим вектором6.3:
, разделенные
малым расстоянием. Пусть координаты этих точек соединяются бесконечно
малым вектором, квадратом которого можно пренебречь по сравнению с
самим вектором6.3:
Пусть задано некоторое скалярное поле
![]() . Вычислим значение
поля
. Вычислим значение
поля ![]() в точке
в точке ![]() если значение этого поля в точке
если значение этого поля в точке ![]() задано:
задано:
Естественно, в этом разложении ![]() в ряд Тейлора можно пренебречь
квадратичными поправками и поправками более высоких степеней. Величина:
в ряд Тейлора можно пренебречь
квадратичными поправками и поправками более высоких степеней. Величина:
называется производной Ли от скалярного поля. В курсах высшей математики
этот оператор чаще называется производной по направлению ![]() .
.
Рассмотрим смысл такой производной на примере скалярного поля, заданного в
трехмерном пространстве. Пусть у нас задано цилиндрически - симметричное
распределение температуры в пространстве с цилиндрическими координатами
![]() ,
, ![]() и
и ![]() . Интуитивно понятно, что температура может зависеть
от радиуса
. Интуитивно понятно, что температура может зависеть
от радиуса ![]() , но она не будет зависеть от координаты
, но она не будет зависеть от координаты ![]() или от
координаты
или от
координаты ![]() . Это означает, что производная от температуры
по координатам
. Это означает, что производная от температуры
по координатам ![]() ,
, ![]() равна нулю. В инвариантном виде это означает,
что существуют вектора, выделяющие направление вдоль которых производная Ли
равна нулю. В данном частном случае это вектора описывающие движения вдоль
оси
равна нулю. В инвариантном виде это означает,
что существуют вектора, выделяющие направление вдоль которых производная Ли
равна нулю. В данном частном случае это вектора описывающие движения вдоль
оси ![]() и вокруг нее. В общем случае движение, которое описывает вектор
и вокруг нее. В общем случае движение, которое описывает вектор
![]() , описывает точечную симметрию, если значение поля
, описывает точечную симметрию, если значение поля ![]() в двух
точках
в двух
точках ![]() и
и ![]() вдоль этого вектора является постоянным.
вдоль этого вектора является постоянным.
Теперь определим производную Ли для векторного поля
![]() . От
случая скалярного поля эта производная отличается тем, что теперь
вычисляется величина, которая зависит от координатной системы.
Итак, вновь у нас есть две точки, которые разделены бесконечно малым
вектором
. От
случая скалярного поля эта производная отличается тем, что теперь
вычисляется величина, которая зависит от координатной системы.
Итак, вновь у нас есть две точки, которые разделены бесконечно малым
вектором ![]() . Значения векторного поля в точке
. Значения векторного поля в точке ![]() через значения
в точке
через значения
в точке ![]() вычисляются как:
вычисляются как:
Рассмотрим теперь преобразование координат:
где ![]() - тот же самый вектор бесконечно малой величины.
Теперь, как нетрудно видеть, точка
- тот же самый вектор бесконечно малой величины.
Теперь, как нетрудно видеть, точка ![]() имеет те же значения координат в
тильдованной системе, что и точка
имеет те же значения координат в
тильдованной системе, что и точка ![]() в нетильдованной системе.
Коэффиценты в матрице преобразования векторов для такого преобразования
имеют вид:
в нетильдованной системе.
Коэффиценты в матрице преобразования векторов для такого преобразования
имеют вид:
Соответственно коэффиценты в матрице преобразования вектора в точке ![]() есть:
есть:
или
Запищем теперь значение вектора в точке ![]() через значение в точке
через значение в точке ![]() ,
тогда получим:
,
тогда получим:
Разница между преобразованными компонентами векторного поля в точке ![]() и
непреобразованными компонентами векторного поля в точке
и
непреобразованными компонентами векторного поля в точке ![]() называется
дифференциалом Ли или производной Ли:
называется
дифференциалом Ли или производной Ли:
Аналогично можно определить производную Ли для тензорного поля. Рассмотрим
теперь какое - либо тензорное поле, например, образованное из тензора
второго ранга, которое в системе координат без тильды имеет компоненты
![]() . В преобразованной системе координат оно имеет вид:
. В преобразованной системе координат оно имеет вид:
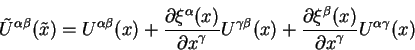
Так отличаются компоненты тензора ![]() в тильдованной и нетильдованной
системах координат. Теперь вычислим компоненты этого тензора в точках
в тильдованной и нетильдованной
системах координат. Теперь вычислим компоненты этого тензора в точках ![]() и
и ![]() .
.
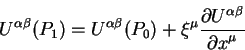
Окончательно вычислим разницу между значениями компонент тензора в точке
![]() в нетильдованной системе координат и значениями компонент тензора в
точке
в нетильдованной системе координат и значениями компонент тензора в
точке ![]() в тильдованной системе координат. Эта величина называется
производной Ли для тензоров второго ранга:
в тильдованной системе координат. Эта величина называется
производной Ли для тензоров второго ранга:
Теперь можно определить симметрию тензорного поля ![]() относительно
векторного поля
относительно
векторного поля ![]() как равенство нулю производной Ли
(6.20).
как равенство нулю производной Ли
(6.20).
Вернемся теперь к симметриям метрического тензора. Производная Ли
метрического тензора выглядит особенно просто:
Это просто проверяется непосредственным вычислением. Равенство нулю
производной Ли дает нам уравнение Киллинга:
которое определяет симметрии метрического тензора.
<< 5. Неэвклидова геометрия | Оглавление | 7. Тензор кривизны >>
|
Публикации с ключевыми словами:
Общая теория относительности - специальная теория относительности - системы отсчета - измерение времени
Публикации со словами: Общая теория относительности - специальная теория относительности - системы отсчета - измерение времени | |
См. также:
Все публикации на ту же тему >> | |